Osová súmernosť

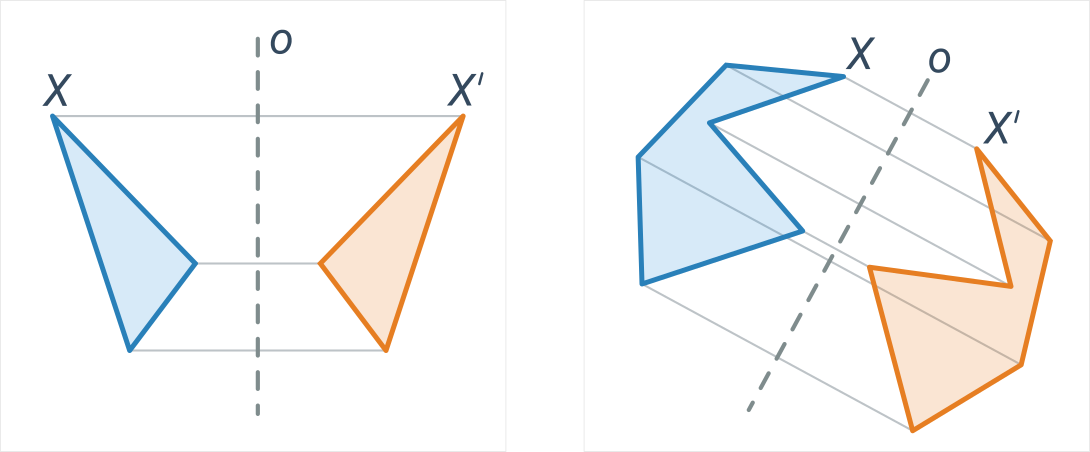
Osová súmernosť je daná priamkou o a priraďuje každému bodu X mimo os taký bod X', že priamka o je osou úsečky XX'. Inými slovami: obraz má od osi rovnakú vzdialenosť ako pôvodný bod a spojnica bodov je kolmá na os. Osová súmernosť zachováva vzdialenosti aj uhly, ide teda o druh zhodnosti.

Príklady

Modré a oranžové útvary sú vzájomne osovo súmerné podľa osi o:

Pre lepšie pochopenie môže byť užitočné porovnať osovú a stredovú súmernosť.

Osovo súmerný útvar

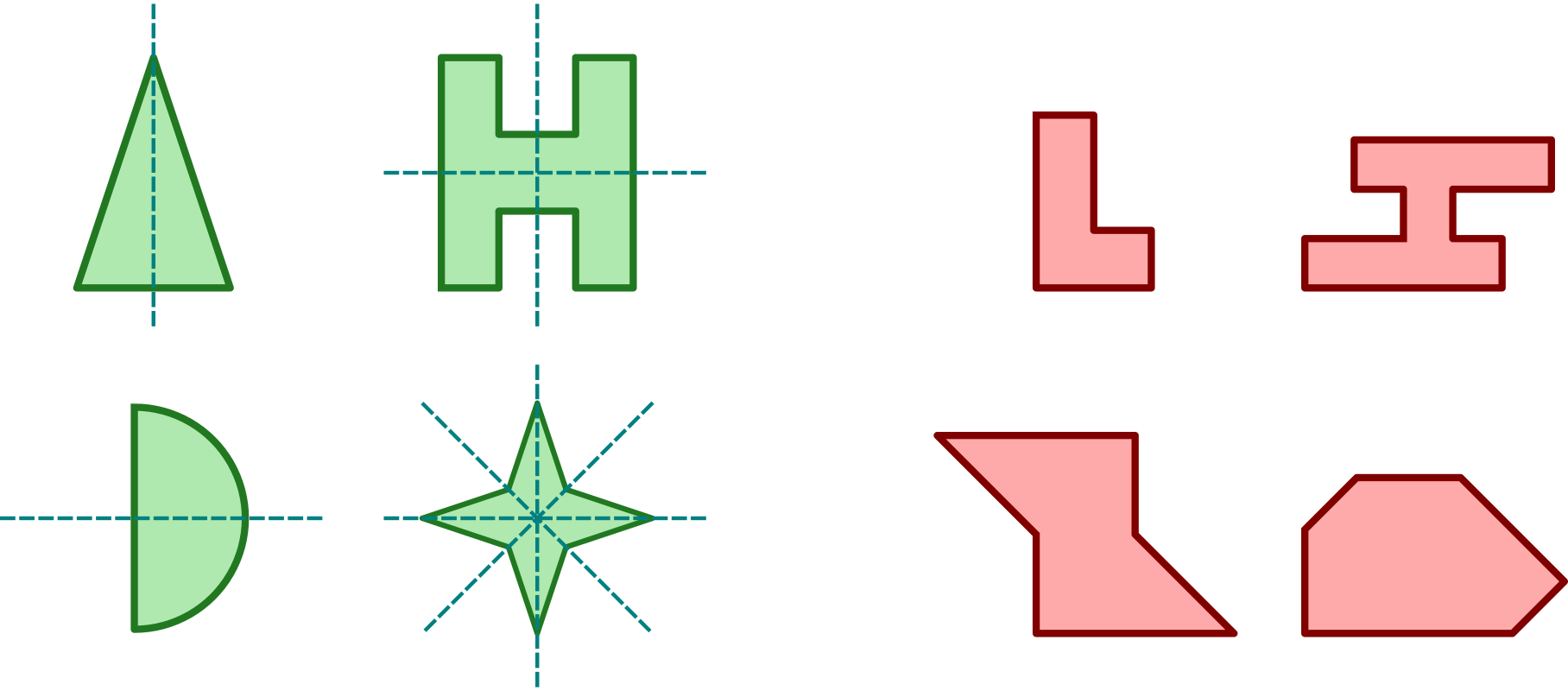
Útvar označujeme za osovo súmerný, ak je v nejakej osovej súmernosti obrazom seba samého. Os tejto súmernosti potom nazývame osou útvaru. Obrázok uvádza príklady útvarov osovo súmerných (zelené, s vyznačenými osami súmernosti) aj tých nesúmerných (červené):

Ďalšie príklady:

• Úsečka je osovo súmerná a má v rovine jedinú os súmernosti (kolmicu v jej strede).
• Rovnoramenný trojuholník je osovo súmerný.
• Trojuholník, ktorý nie je rovnoramenný, nie je osovo súmerný.
• Všetky pravidelné mnohouholníky sú osovo súmerné. Počet osí súmernosti je rovný počtu vrcholov mnohouholníka.
• Kruh je osovo súmerný a má nekonečne veľa osí súmernosti.