Pomery

Pomer dvoch alebo viacerých kladných čísel je vzťah ich veľkostí.

V úvodnom precvičovaní sa stretneme s pojmami ako pomer v základnom tvare, postupný pomer, prevrátený pomer a zistíme, aký je rozdiel medzi pomerom a zlomkom.

Najjednoduchšie použitie pomeru je rozdelenie čísla na časti a zmena (zmenšenie alebo zväčšenie) čísla v zadanom pomere. Nasledujú pokročilejšie výpočty s pomermi, ktoré zahŕňajú aj slovné úlohy vedúce na riešenie rovníc.

Mierka mapy je špeciálny prípad pomeru. S pomermi ďalej súvisí téma podobnosť v geometrii.

Pomer dvoch kladných hodnôt, napr. 2:4, vyjadruje vzťah ich veľkostí.

• Dedko našiel 10 dubákov a 1 bedľu. Pomer počtu dubákov k počtu bedlí v dedkovom košíku je 10:1.

Podobne ako v prípade zlomkov môžeme pomery krátiť a rozširovať kladnými číslami.

• Pomer počtu dubákov k počtu bedlí 10:1 môže byť úplne rovnako vyjadrený ako 20:2 nebo 1:0{,}1.

Pomer, ktorý je vyjadrený dvomi celými číslami a nejde už viac skrátiť, je v základnom tvare.

• Základný tvar pomeru 2:4 je 1:2.

Je možné zapísať aj pomer viac než dvoch hodnôt, potom ide o postupný pomer.

• Kaleráby, reďkovky a mrkvy nám na záhrade vyrástli v pomere 2 : 10 : 11.

Prevráteným pomerom k pomeru a:b myslíme pomer b:a.

• Pomer objemov sirupu a vody v nápoji je 1:10, prevrátený pomer 10:1 značí pomer objemov vody k sirupu.

Aký je rozdiel medzi pomerom a zlomkom? Pomer popisuje vzťah dvoch častí. Zlomok je časť z celku.

Zmena čísla

Zmena čísla v zadanom pomere a:b je vynásobenie čísla zodpovedajúcim zlomkom \frac{a}{b}.

• Ak je a < b a teda \frac{a}{b}<1, budeme číslo zmenšovať.
• Ak je a > b a teda \frac{a}{b}>1, budeme číslo zväčšovať.

Príklad: Zmena čísla 10 v pomere 2:5 znamená vynásobenie čísla 10 zlomkom \frac{2}{5}. Vyjde nám číslo 4.

Rozdelenie čísla

Rozdelenie čísla v zadanom pomere a:b znamená rozdelenie čísla na dve časti, ktoré sú v pomere a:b.

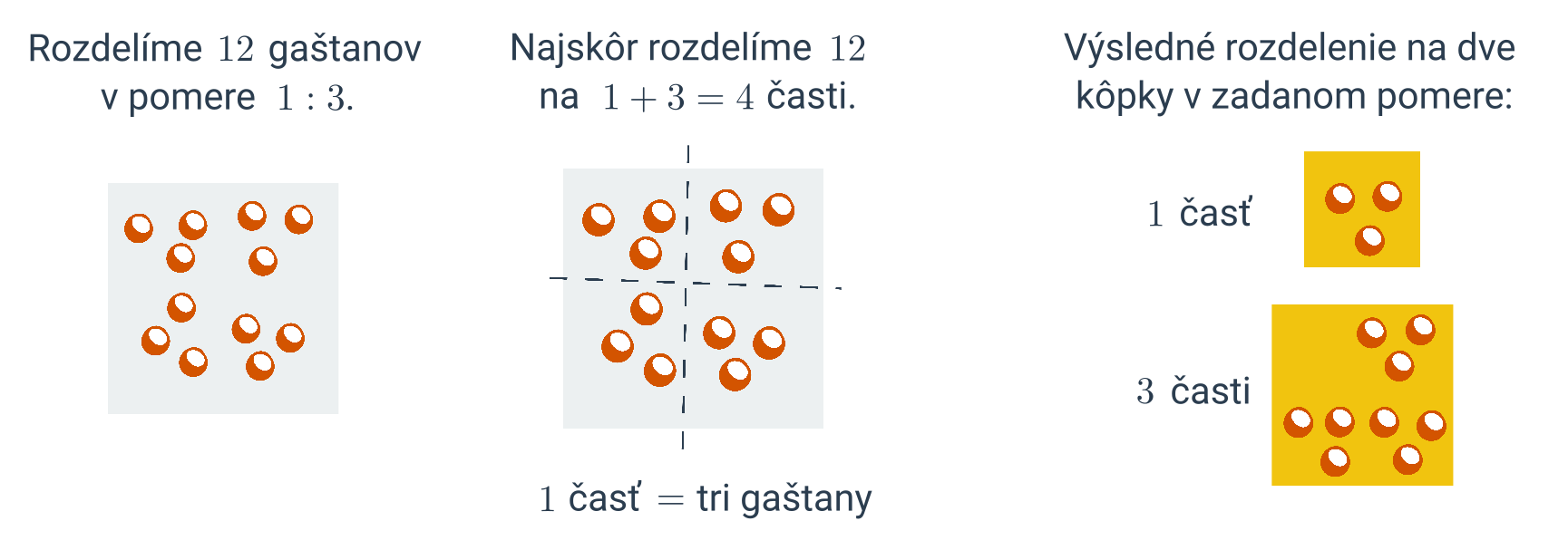
Príklad: Rozdeľte číslo 30 v pomere 2:3. Celkovo budeme rozdeľovať na 2+3=5 častí. Jedna časť sa teda rovná \frac{30}{5}=6. Výsledné čísla sú rovné 2 častiam, teda 2\cdot 6= 12, a 3 častiam, teda 3\cdot 6=18. Rozdelili sme číslo 30 v pomere 2:3 na 12 a 18.

Výpočty pri znalosti súčtu (rozdielu)

Hľadáme dve čísla, keď poznáme ich pomer a poznáme ich súčet (prípadne rozdiel, súčin, alebo nejaký iný výraz). V takom prípade nám väčšinou pomôže vypočítať si najskôr čomu zodpovedá jedna časť pomeru. Väčšinou pokračujeme výpočtom hľadaných čísel podľa toho, koľkým častiam v pomere zodpovedá prvé a druhé číslo.

Príklad: Pomer nabitých a vybitých batérií v Gargamelovom detektore šmolkov je 1:4. Vybitých batérií je pritom o 6 viac než nabitých. Koľko je nabitých a vybitých batérií?

Najskôr si spočítame, koľkým batériám zodpovedá jedna časť. Vieme, že vybitých batérií je o 6 viac než nabitých. Vybitých batérií sú pritom 4 časti a nabitých 1 časť, takže vybitých je o 4-1=3 časti viac než nabitých. Takže 3 časti zodpovedajú 6 batériám. Jedna časť zodpovedá \frac{6}{3}=2 batériám. Gargamel má teda 2 nabité batérie a 4 \cdot 2 = 8 vybité batérie.

Výsledok: Gargamel má dve nabité a osem vybitých batérií.

Výpočty pomocou rovníc

Ak nám už ide riešenie rovníc, môžeme pri riešení využiť zápis pomocou dvoch rovníc pre dve neznáme.

• Prvú rovnicu zapíšeme zo známeho pomeru.
• Druhú rovnicu zapíšeme z informácie o hodnote súčtu (alebo rozdielu, súčinu, atď.).

Príklad (ťažší príklad pre tých, ktorí už poznajú rovnice a obvod kruhu): Vieme, že polomery dvoch kruhov sú v pomere 2 : 5 a že súčet ich obvodov je 70 \pi. O aké polomery ide?

Označíme si polomery a a b a zapíšeme si rovnice. Poznáme pomer a : b = 2 : 5, takže máme prvú rovnicu \frac{a}{b}=\frac{2}{5}. Súčet obvodov kruhov s polomermi a,b je rovný 2a\cdot \pi + 2b\cdot \pi. Tento súčet poznáme, takže druhá rovnica je 2(a+b)\cdot\pi = 70 \pi.

Riešime sústavu rovníc. Prvú rovnicu vynásobíme 5b (má zmysel pre b\neq 0) a dostaneme 5a=2b. Vydelíme druhú rovnicu kladným číslom 2\pi a dostaneme a+b=35. Vyjadríme a z druhej rovnice a dosadíme do prvej. 5\cdot(35-b)=2b. Zjednodušíme a vypočítame b. 175= 7b, tedy b=25. Vypočítame druhý polomer a=35-b=10.

Výsledné polomery kruhov sú a=10,b=25.

Mierka mapy je špeciálny prípad pomeru. Ide o pomer, v ktorom je obraz krajiny na mape v pomere ku krajine v skutočnosti.

Príklady

• Mapa s mierkou 1 : 10\,000. Centimeter na tejto mape zodpovedá 10\,000\ \text{cm} = 100\ \text{m} v skutočnosti.
• Nákres, na ktorom je dĺžka päťmetrovej sochy 2\ \text{cm}, má mierku 2 : (100\cdot 5) = 2 : 500 = 1 : 250.