Predchádzajúce
Cvičenie
Grafom funkcie danej predpisom y= ax+b je priamka. Množinou riešení lineárnej nerovnice budú všetky body [x,y] ležiace v polrovine s hraničnou priamkou y= ax+b. Môže nastať jedna zo štyroch možností:
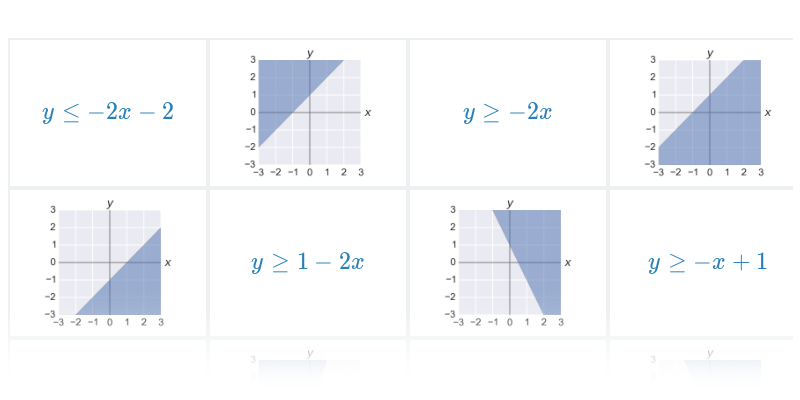
| y\geq ax+b | Nerovnosť spĺňajú všetky body v rovine, ktoré ležia priamo na priamke danej rovnicou y=ax+b alebo „nad“ touto priamkou (so súradnicou y väčšou než ax+b). |
| y \gt ax+b | Nerovnosť spĺňajú všetky body v rovine, ktoré ležia „nad“ priamkou s rovnicou y=ax+b. |
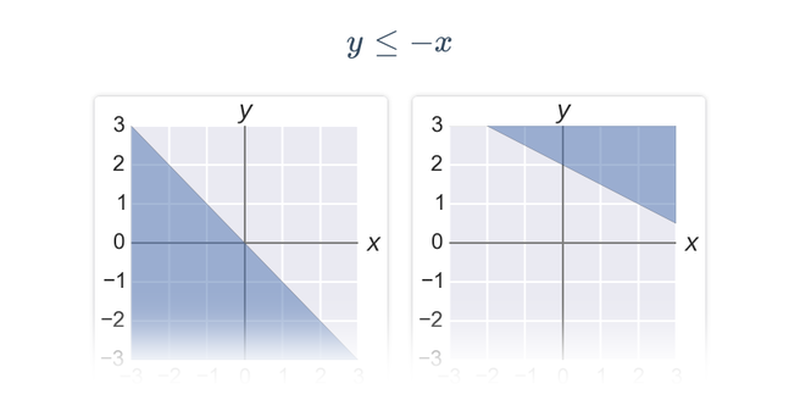
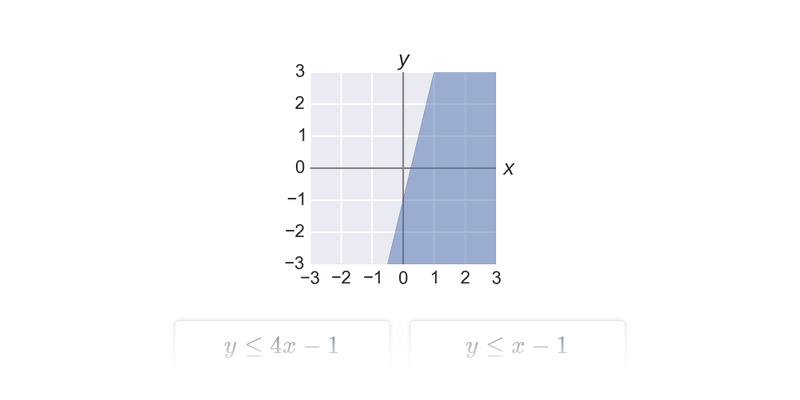
| y\leq ax+b | Nerovnosť spĺňajú všetky body v rovine, ktoré ležia na priamke s rovnici y=ax+b alebo „pod“ touto priamkou (so súradnicou y menšou než ax+b). |
| y \lt ax+b | Nerovnosť spĺňajú všetky body v rovine, ktoré ležia „pod“ priamkou s rovnicou y=ax+b. |
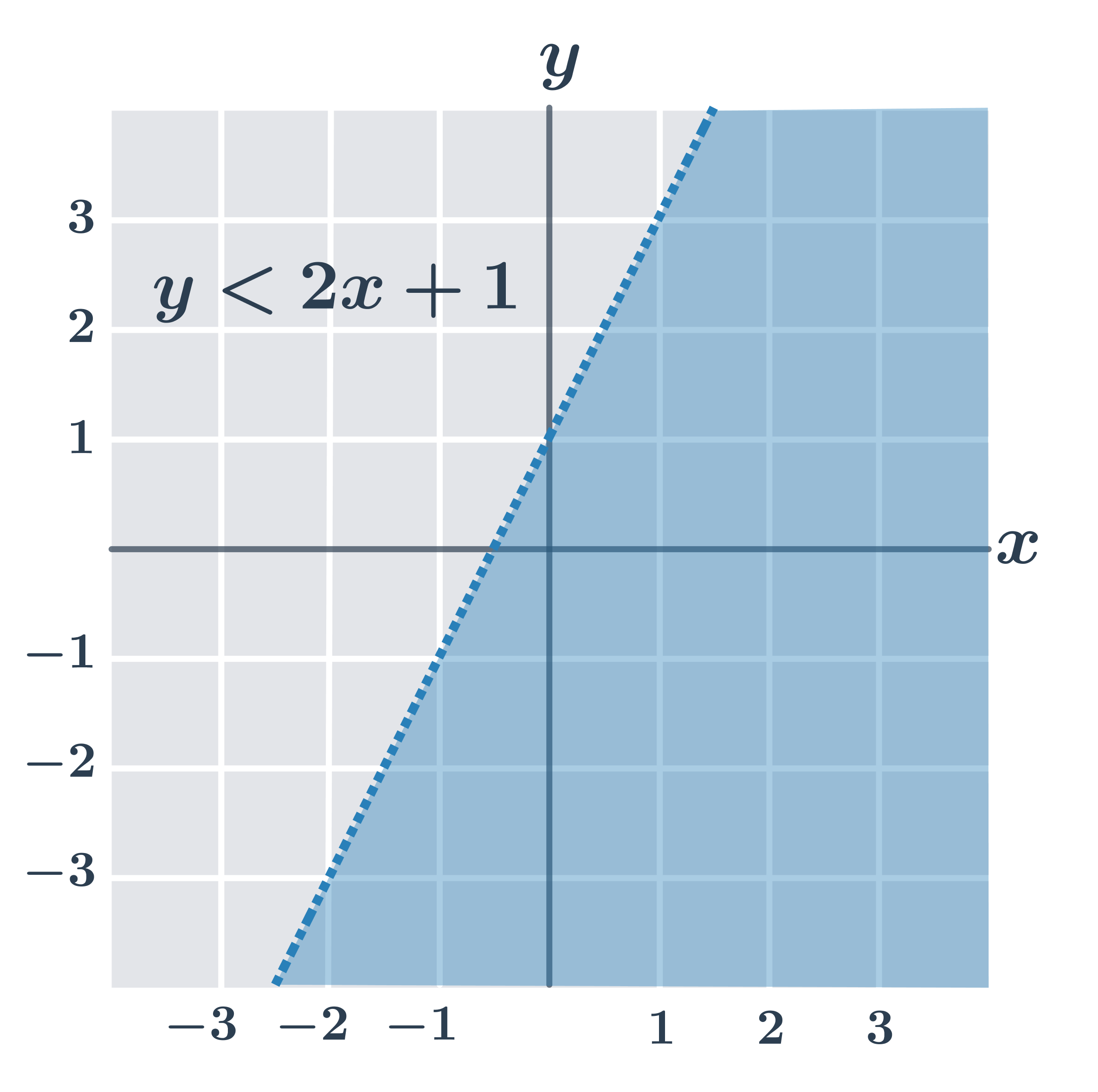
Na obrázkoch sú riešenia všetkých typov lineárnych nerovníc (všimnite si, že ak je v nerovnici iba znamienko \gt alebo \lt, body priamo na hraničnej priamke lineárnu nerovnicu nespĺňajú).
- y\geq 2x+1
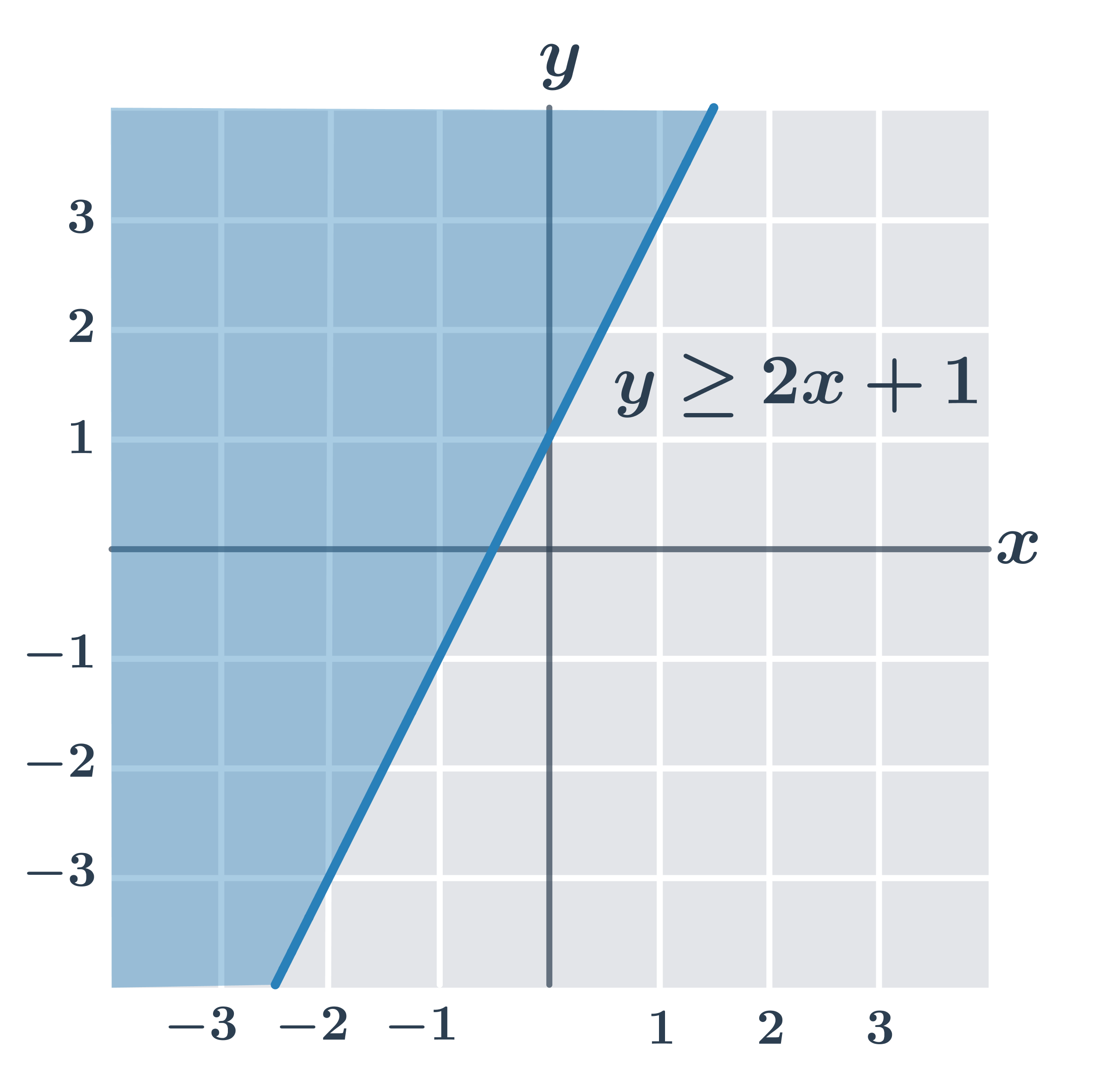
- y \gt 2x+1
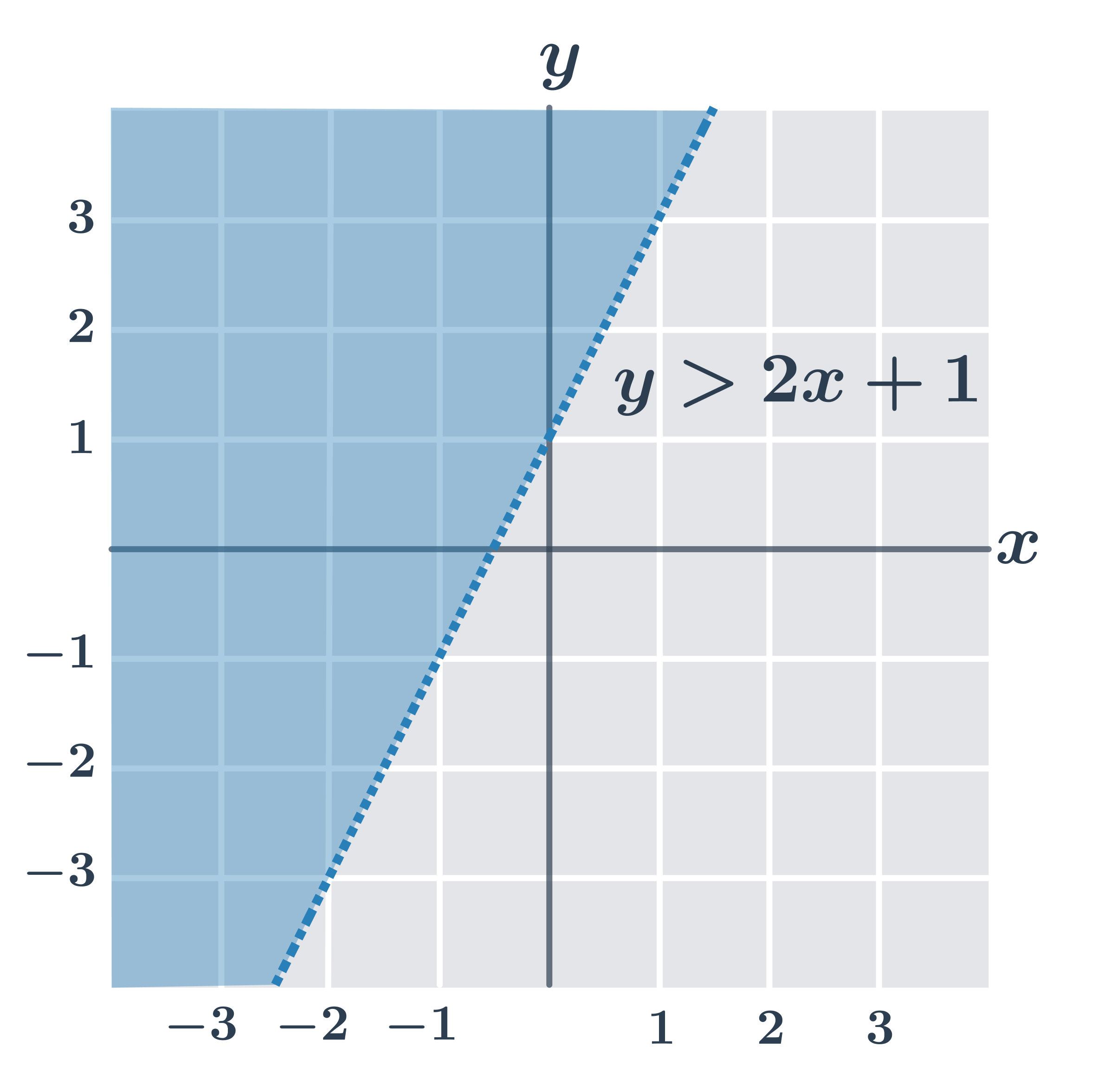
- y\leq 2x+1
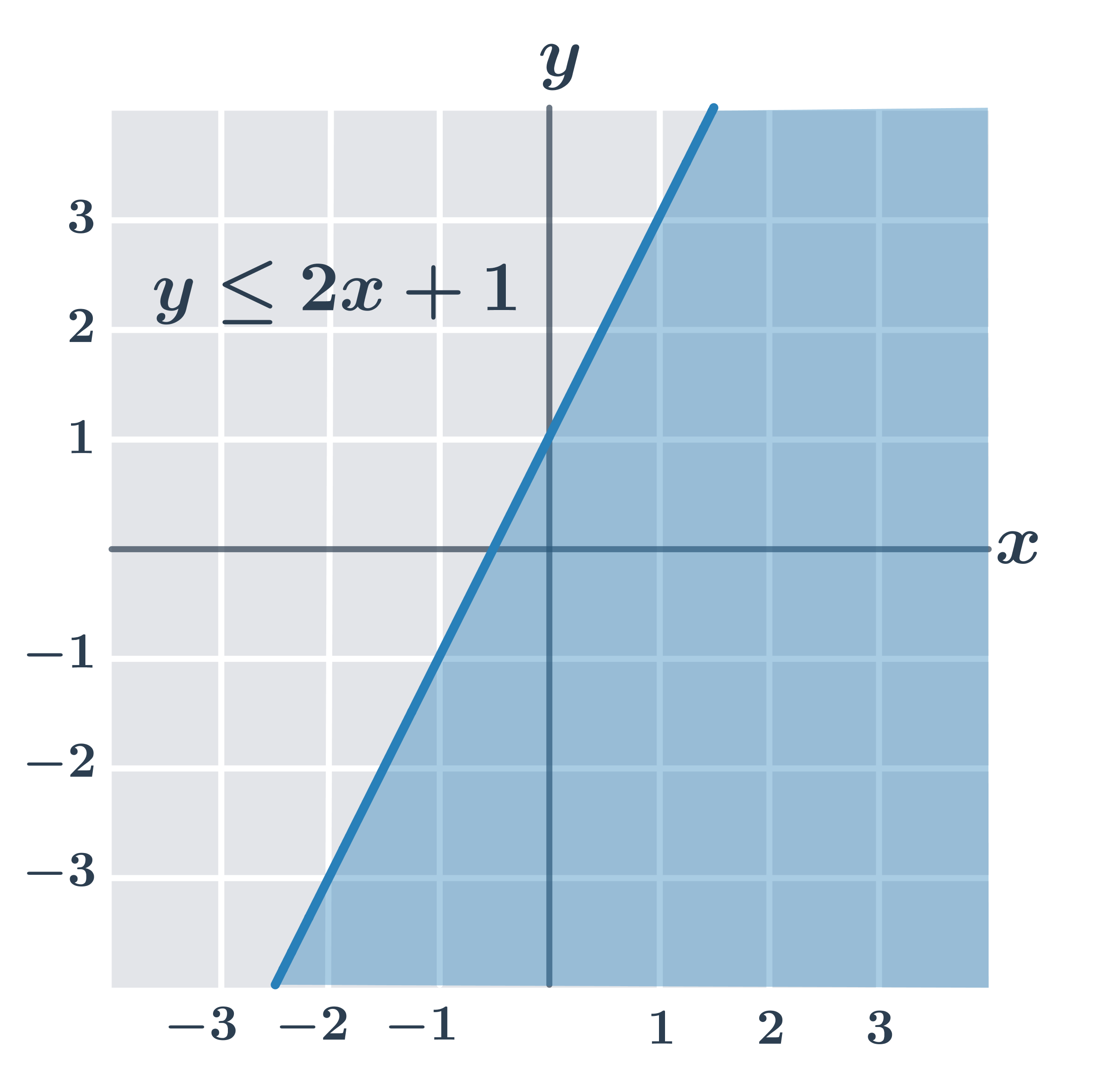
- y \lt 2x+1
Vysvetlenie mi pomohlo
Vysvetlenie mi nepomohlo
Rozhodovačka
Rýchle precvičovanie výberom z dvoch možností.
Grafy lineárnych nerovníc 
Zobraziť súhrn témy
stredné
Grafy lineárnych nerovníc (stredné) • EEA
Typicky zaberie: 5 min.
ťažké
Grafy lineárnych nerovníc (ťažké) • FOU
Typicky zaberie: 5 min.
Pexeso
Hľadanie dvojíc, ktoré k sebe patria.
Grafy lineárnych nerovníc
Zobraziť súhrn témy
stredné
Grafy lineárnych nerovníc (stredné) • EDW
Typicky zaberie: 5 min.
