Predchádzajúce
Nadväzujúce
Cvičenie
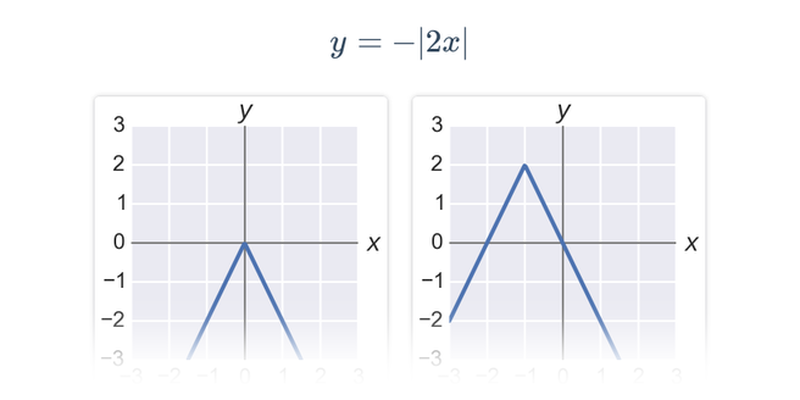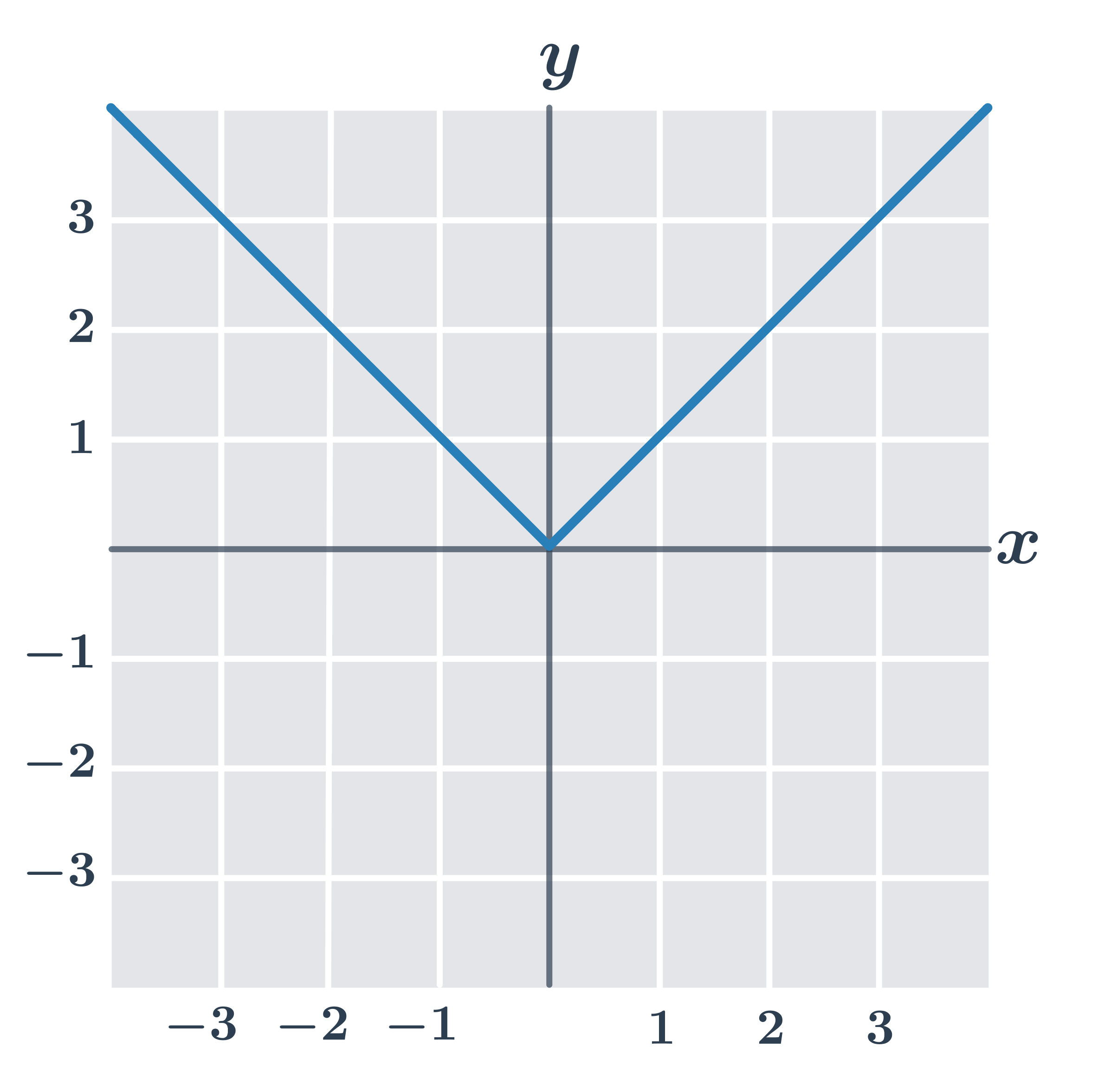
Na obrázku je graf funkcie y=|x|. Tento graf tvoria dve polpriamky s počiatkom v bode [0;0], pretože pre absolútnu hodnotu platí:
- absolútna hodnota kladného čísla je rovná tomuto číslu: |x|=x
- absolútna hodnota záporného čísla je rovná opačnému číslu: |x|=-x
- absolútna hodnota čísla nula je rovná nule: |0|=0
| x \gt 0 | Grafom funkcie y=|x| je polpriamka s počiatkom v bode [0;0] daná rovnicou y=x. |
| x \lt 0 | Grafom funkcie y=|x| je polpriamka s počiatkom v bode [0;0] s rovnicou y=-x. |
| x = 0 | Bod [0;0] je počiatok polpriamok, ktoré vytvoria graf funkcie y=|x|. |
Ak chceme nakresliť graf funkcie y=|f(x)| postupujeme tak, že nakreslíme graf y=f(x) a potom záporné funkčné hodnoty nahradíme opačnými. V oblasti, kde sú funkčné hodnoty záporné, sa teda graf preklopí okolo osi x.
Príklad 1: graf funkcie y=|x-1|
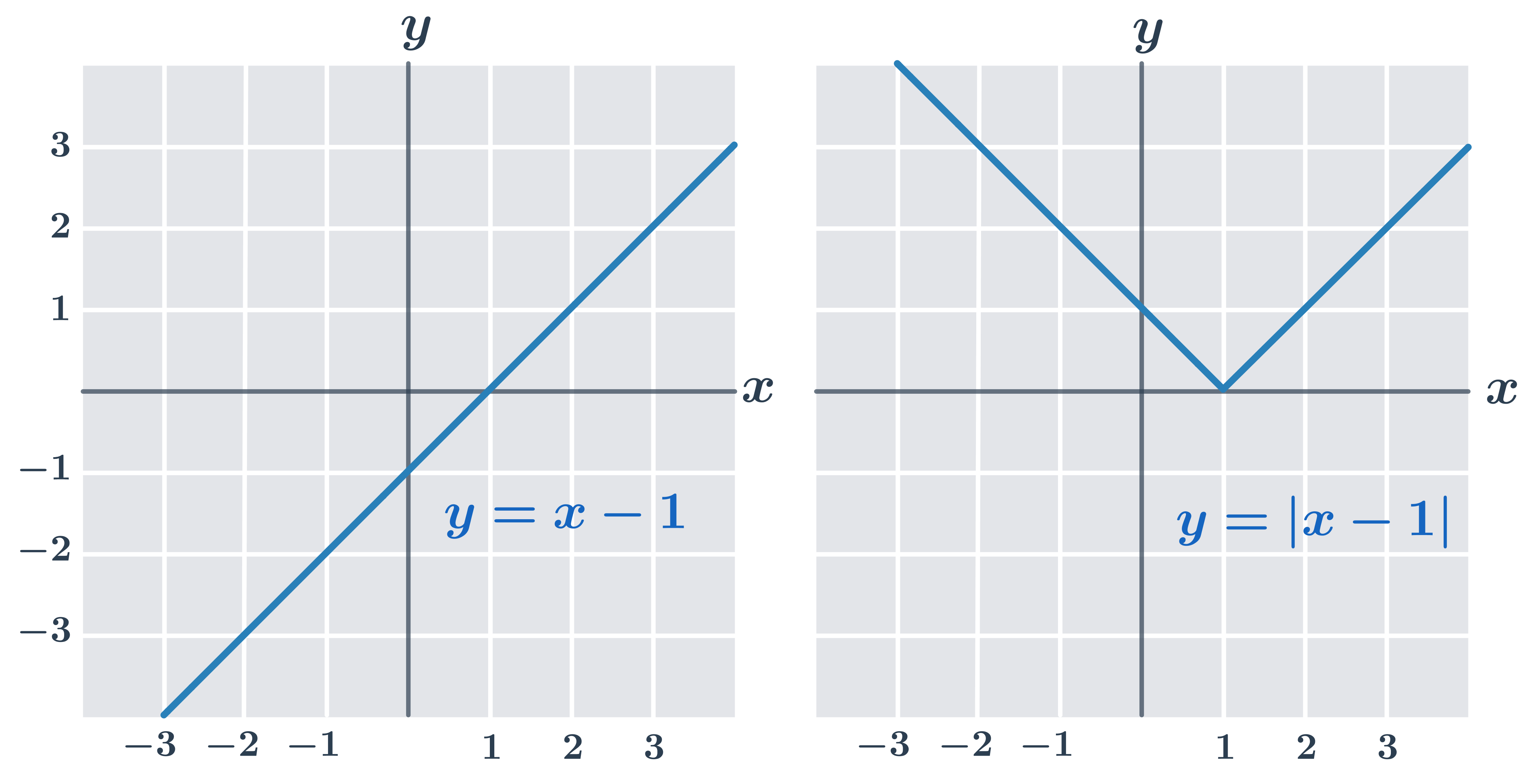
| Pre čísla x \lt 1 má funkcia y=x-1 záporné funkčné hodnoty. |
| Funkcia y=|x-1| má v intervale (-\infty;1) opačné hodnoty než funkcia y=x-1 (graf y=|x-1| je voči grafu y=x-1 v tomto intervale preklopený podľa osi x). |
| V intervale (1;\infty) sú grafy funkcií y=x-1 a y=|x-1| rovnaké. |
Príklad 2: graf funkcie y=|x^2-4|
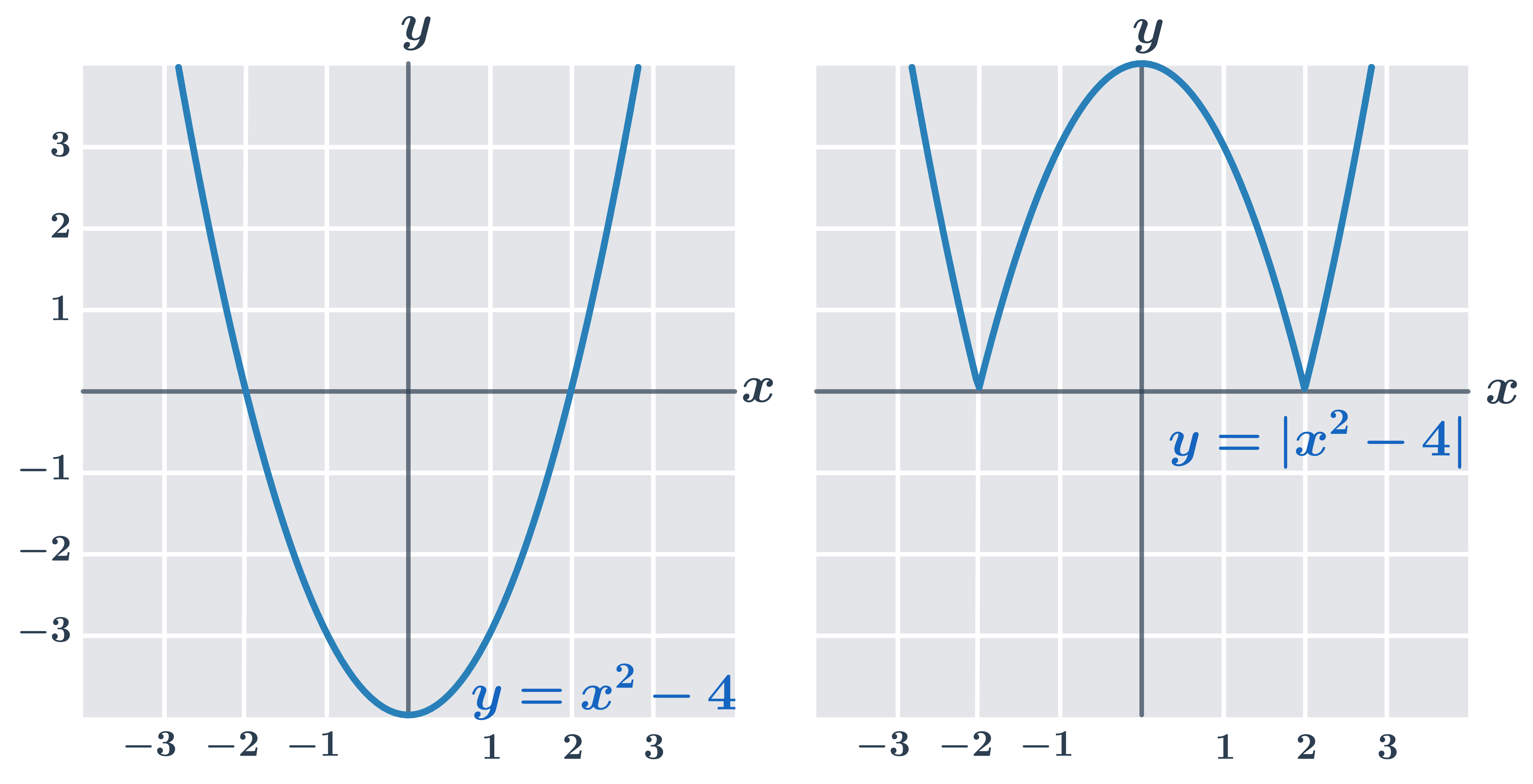
| V intervale (-2;2) má funkcia y=x^2-4 záporné funkčné hodnoty. |
| Funkcia y=|x^2-4| má v intervale (-2;2) opačné hodnoty než funkcia y=x^2-4 (graf je preklopený podľa osi x). |
| V intervaloch (-\infty;-2) a (2;\infty) sú grafy funkcií y=x^2-4 a y=|x^2-4| rovnaké. |
Vysvetlenie mi pomohlo
Vysvetlenie mi nepomohlo
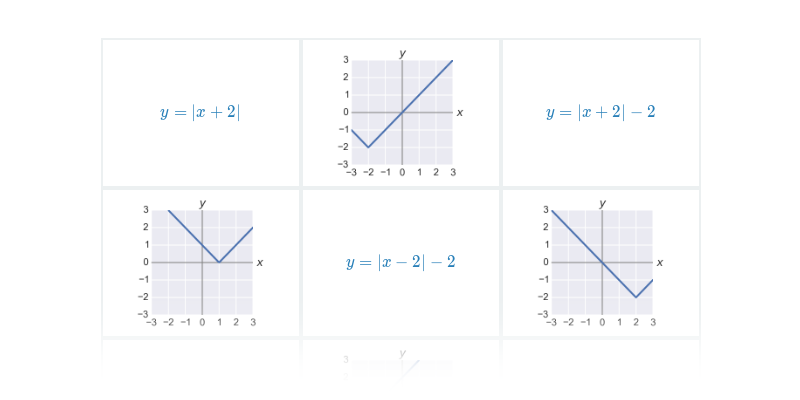
Rozhodovačka
Rýchle precvičovanie výberom z dvoch možností.
Grafy funkcií s absolútnou hodnotou 
Zobraziť súhrn témy
ťažké
Grafy funkcií s absolútnou hodnotou (ťažké) • ED7
Typicky zaberie: 6 min.
Pexeso
Hľadanie dvojíc, ktoré k sebe patria.
Grafy funkcií s absolútnou hodnotou
Zobraziť súhrn témy
ťažké
Grafy funkcií s absolútnou hodnotou (ťažké) • EDT
Typicky zaberie: 7 min.
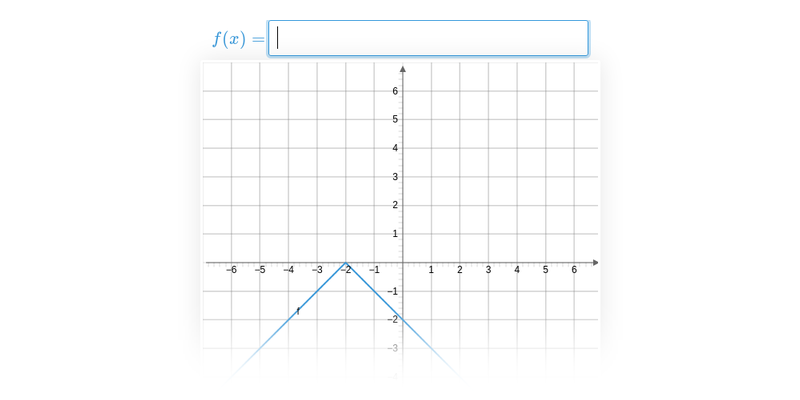
Grafár
Špecializované cvičenie na prácu s grafom a funkciami.
Grafy funkcií s absolútnou hodnotou
Zobraziť súhrn témy
ťažké
Grafy funkcií s absolútnou hodnotou (ťažké) • E6E
Typicky zaberie: 9 min.
