Cvičenie
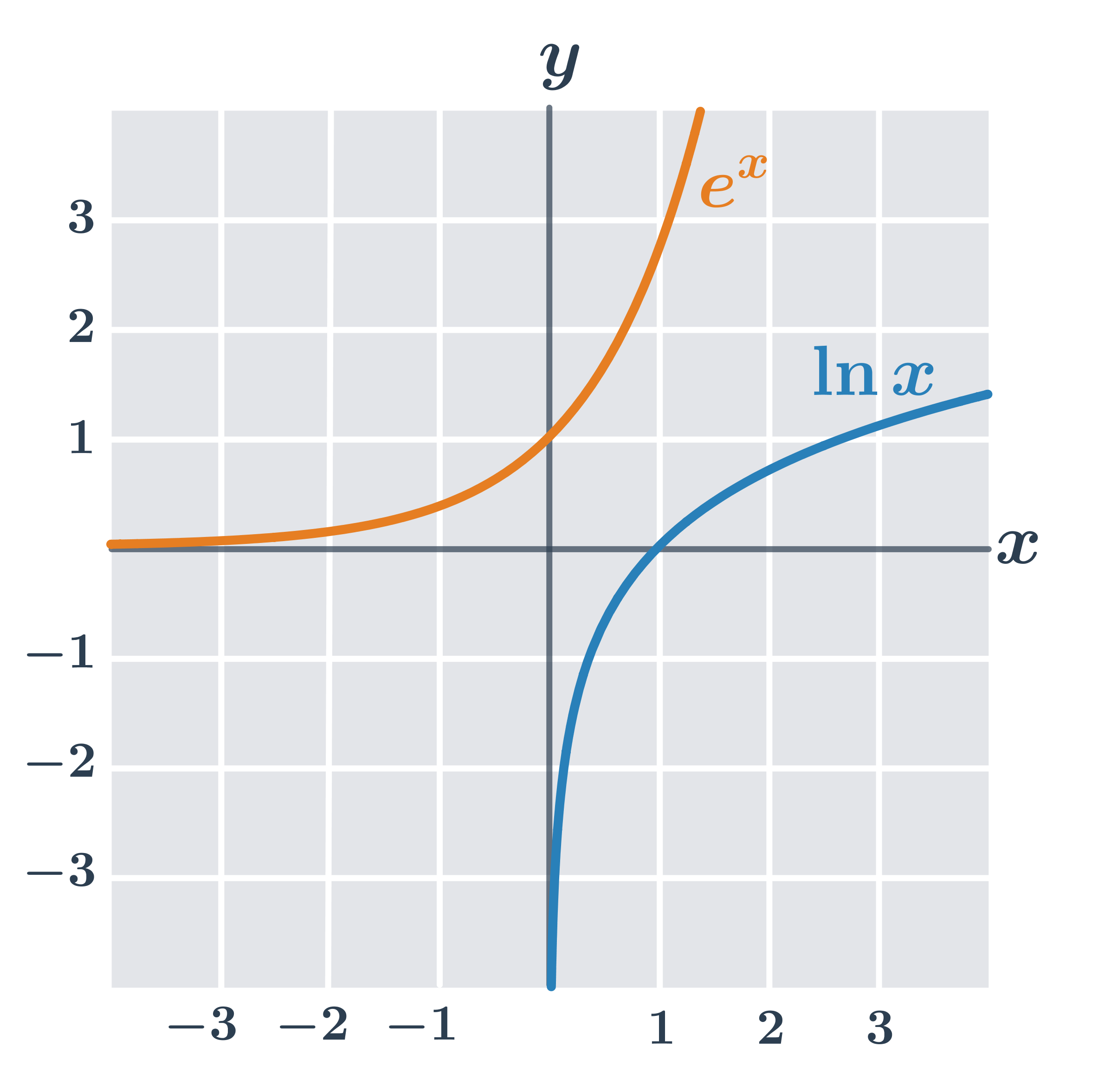
Logaritmická funkcia je inverzná k exponenciálnej funkcii s rovnakým základom. Grafy dvoch navzájom inverzných funkcií sú osovo súmerné podľa osi prvého kvadrantu (teda priamky spĺňajúcej x=y).
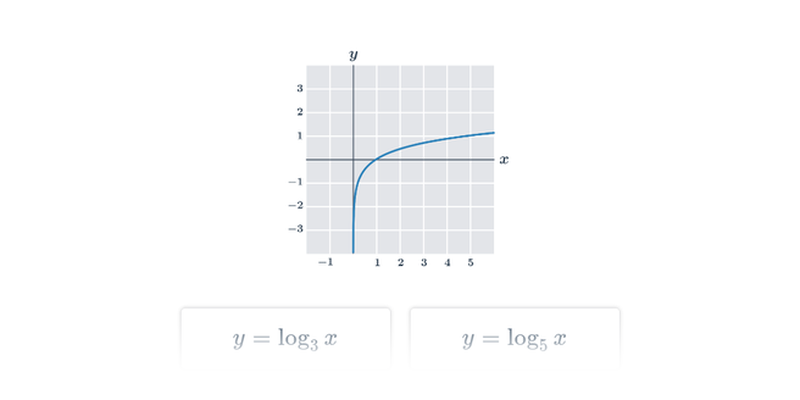
Graf každej logaritmickej funkcie tvaru y=\log_a x prechádza bodom [1,0], pretože pre ľubovoľnú konštantu a platí: \log_a 1=0. Na obrázku vidíme grafy logaritmických funkcií s rôznymi základmi 2, e, 10.
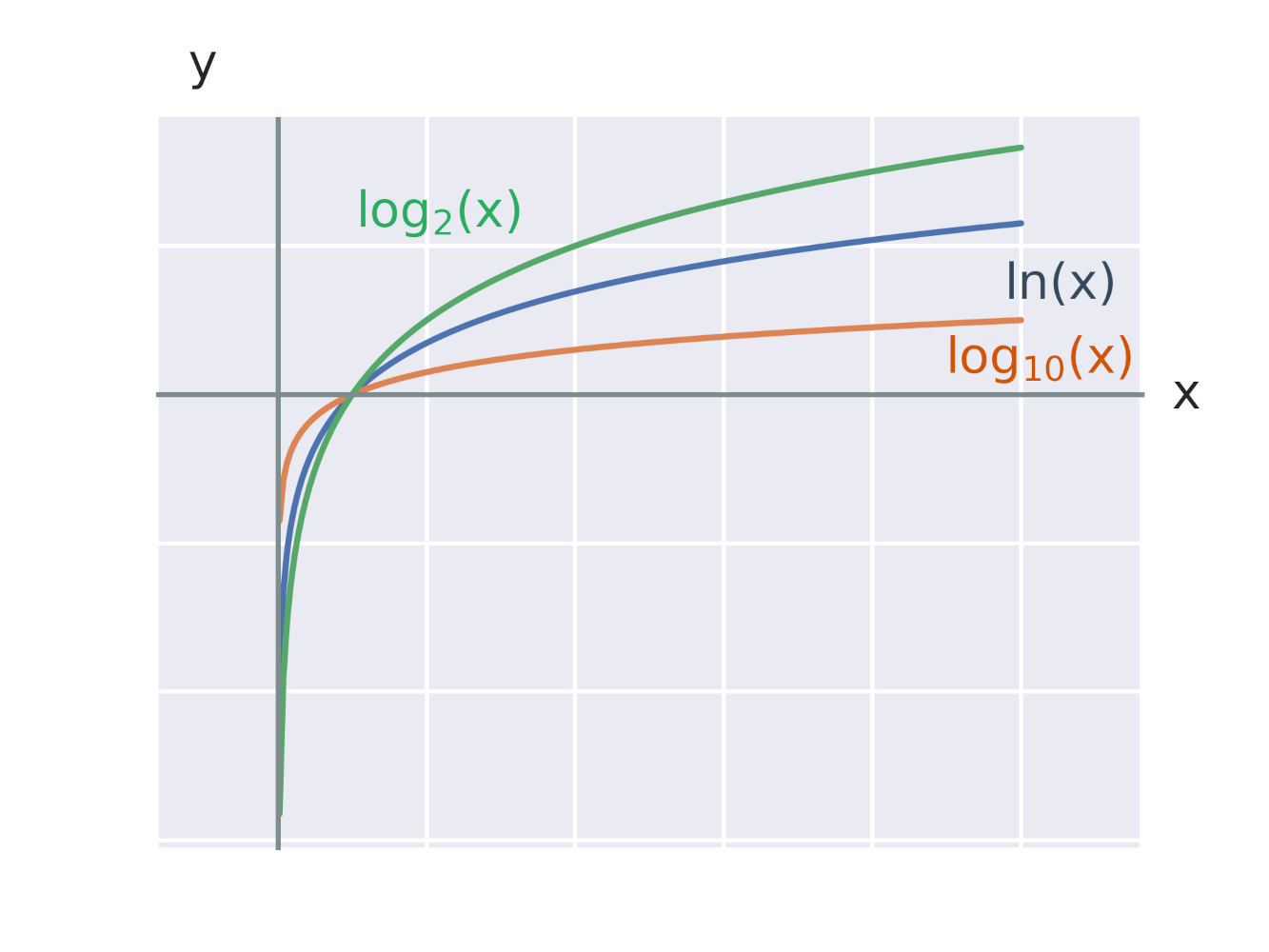
Značenie niektorých význačných logaritmických funkcií:
| funkcia | popis | ďalšie možné značenia |
|---|---|---|
| \log_a x | všeobecne logaritmus x so základom a pre nejaké a >0, a\neq 1 | |
| \ln x | prirodzený logaritmus x, teda logaritmus x so základom e | v angl. textoch niekedy \log x |
| \log x | dekadický logaritmus x, teda logaritmus x so základom 10 | \log_{10}x |
| \log_2 x | binárny logaritmus x, teda logaritmus x so základom 2 | niekedy sa objavuje \mathrm{lb}\;x |
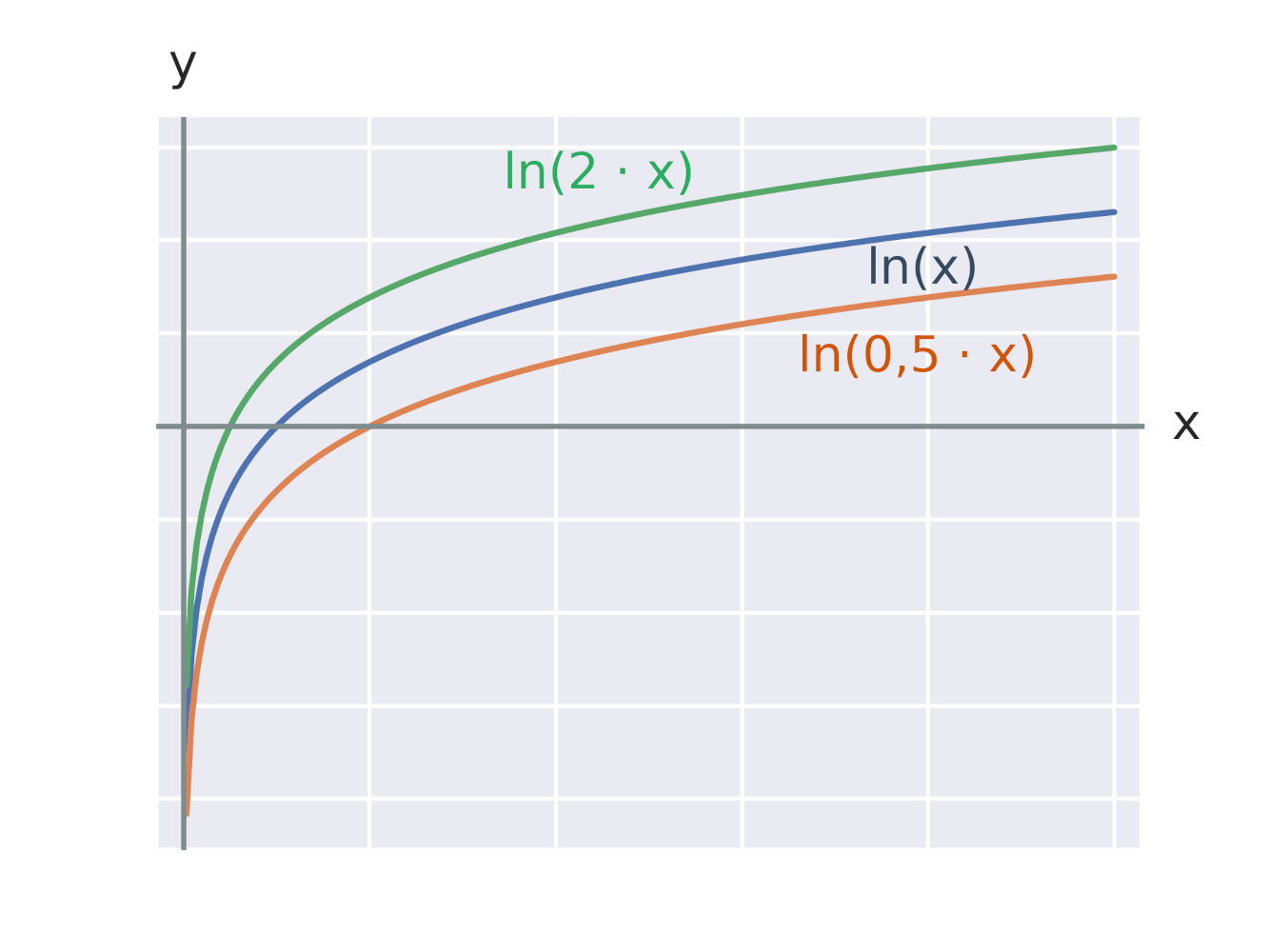
Efekt pripočítania konštanty k logaritmickej funkcii
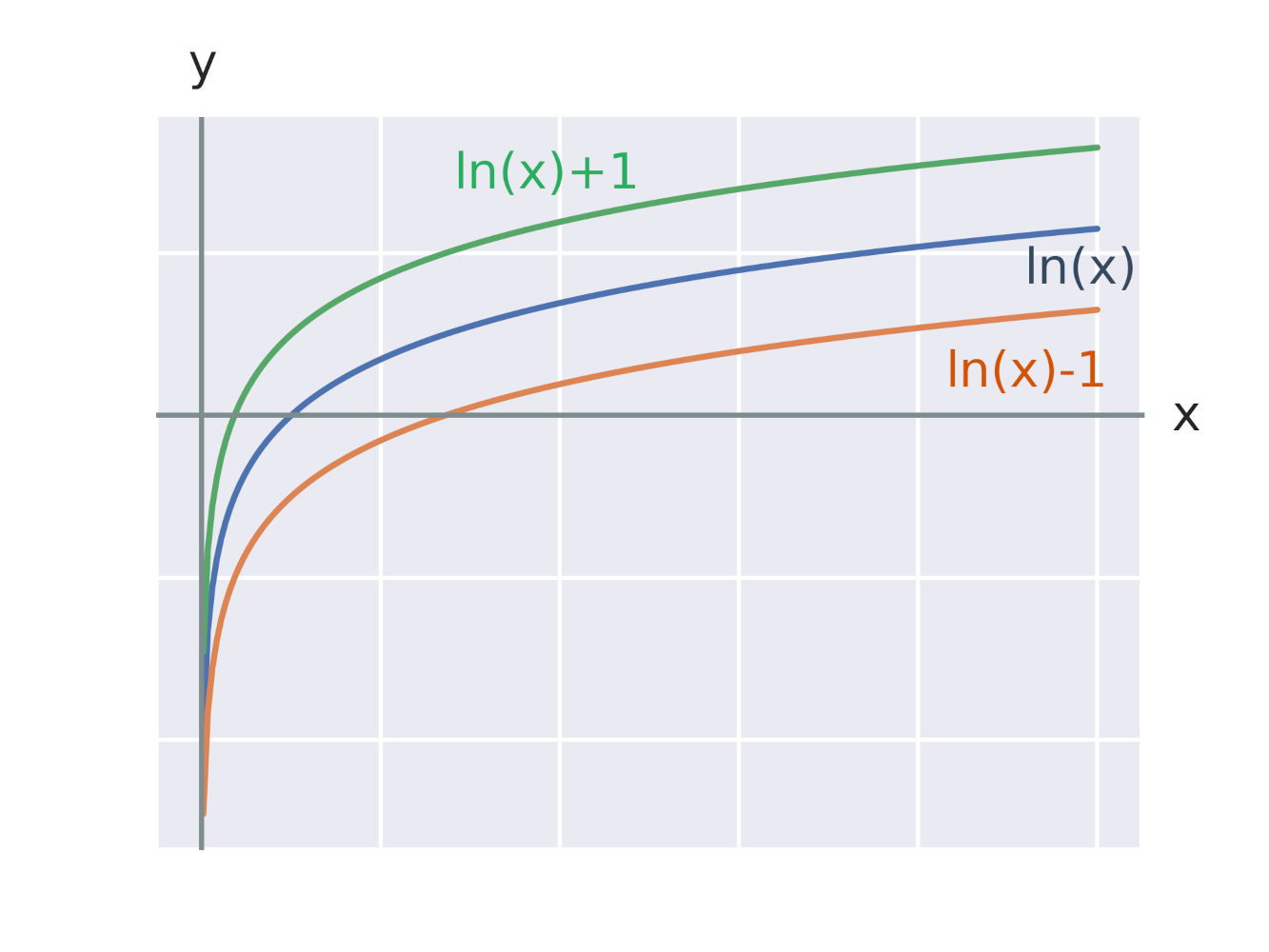
Efekt pripočítania konštanty k argumentu logaritmickej funkcie
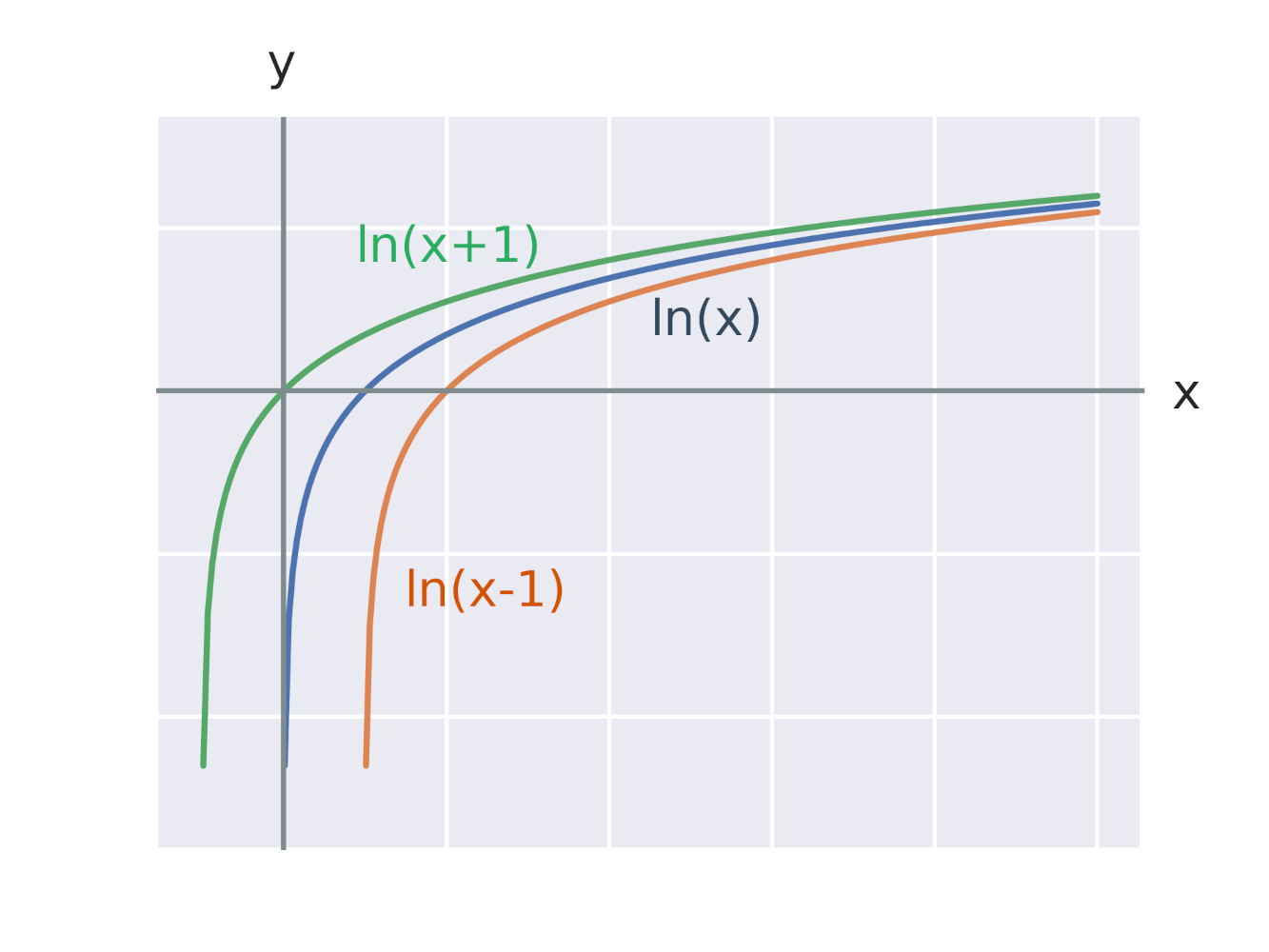
Efekt vynásobenia logaritmickej funkcie konštantou
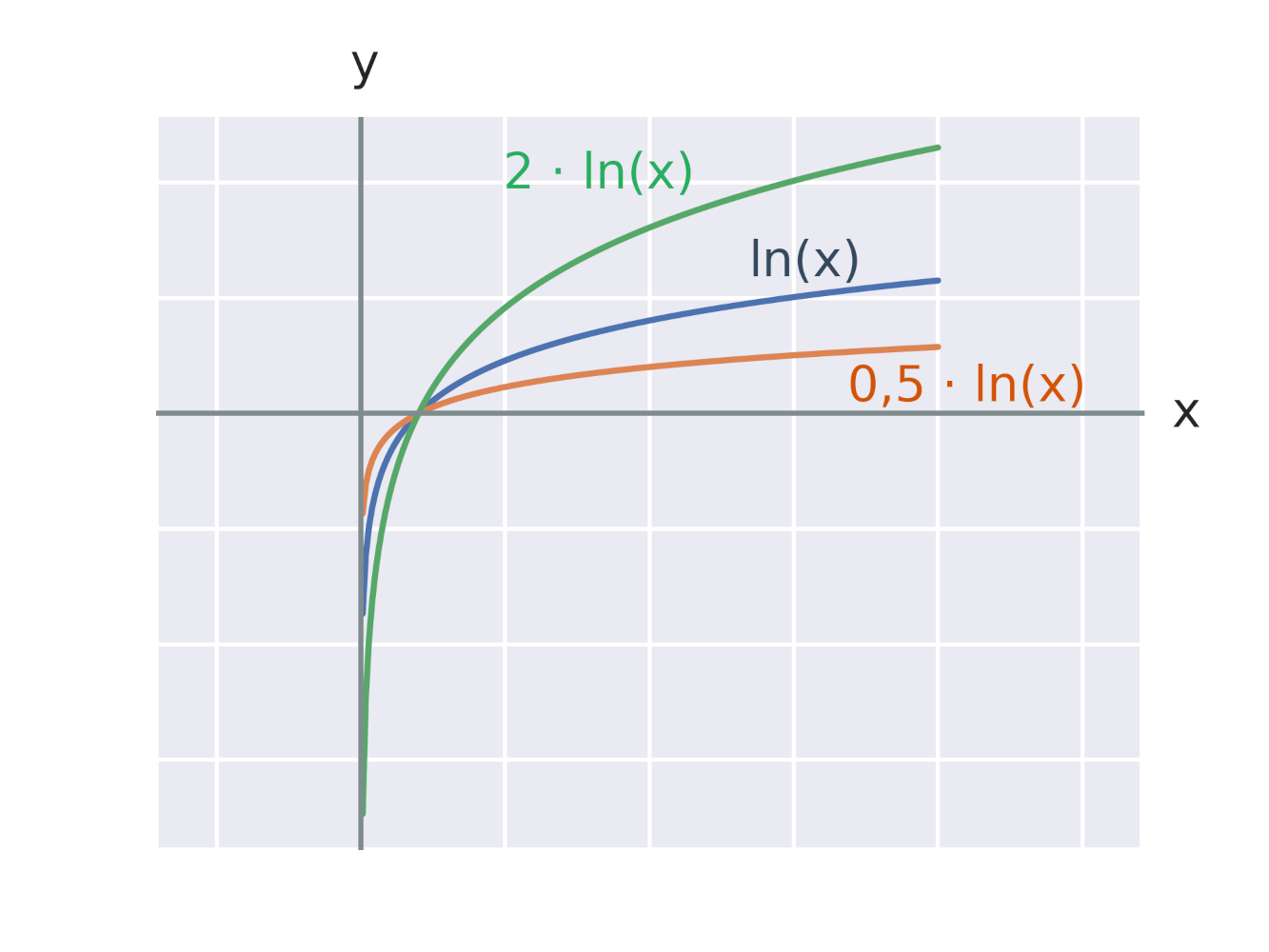
Efekt vynásobenia argumentu logaritmickej funkcie konštantou
Rozhodovačka
Rýchle precvičovanie výberom z dvoch možností.
Grafy logaritmických funkcií 
Zobraziť súhrn témy
ťažké
Grafy logaritmických funkcií (ťažké) • G1X
Typicky zaberie: 5 min.
Grafár
Špecializované cvičenie na prácu s grafom a funkciami.
Grafy logaritmických funkcií
Zobraziť súhrn témy
ťažké
Grafy logaritmických funkcií (ťažké) • G7P
Typicky zaberie: 5 min.
