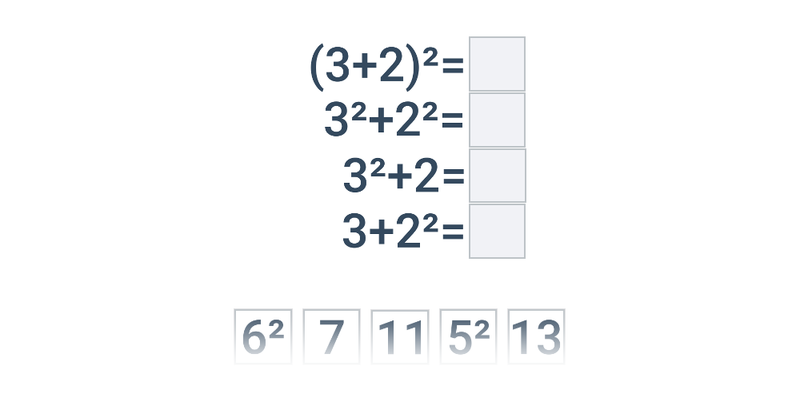Umocňovanie je opakované násobenie. Napríklad 3^5 = 3\cdot 3\cdot 3\cdot 3\cdot 3 = 243. Odmocňovanie je opačnou operáciou k umocňovaniu. Napríklad druhá odmocnina z 36 je 6 (\sqrt{36}=6), pretože 6^2 = 6\cdot 6 = 36. Mocniny a odmocniny využívame v mnohých oblastiach matematiky, napríklad pri práci s mnohočlenmi, riešení kvadratických rovníc, výpočte obsahu a objemu alebo pri určovaní dĺžok strán v trojuholníku.
Prvým krokom pre zvládnutie tejto témy sú základné mocniny a odmocniny, kde pracujeme s malými, prirodzenými číslami. Pre tieto čísla sa vyplatí sa naučiť základné mocniny a odmocniny naspamäť, pretože na ne často v matematike narazíme.
Ako ďalší krok potrebujeme zvládnuť pracovať s výrazmi s mocninami a odmocninami.
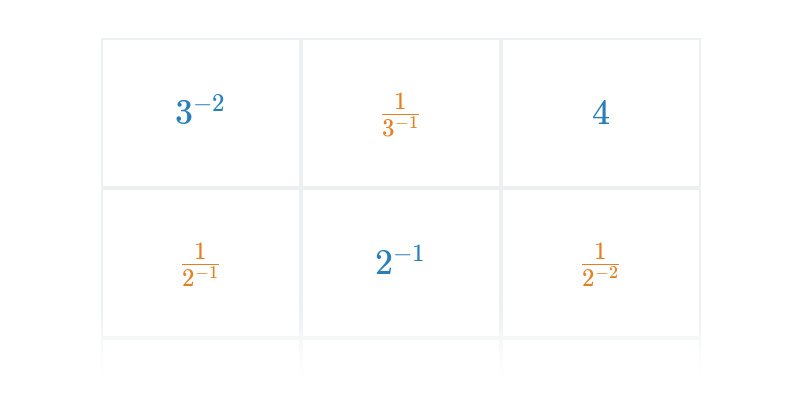
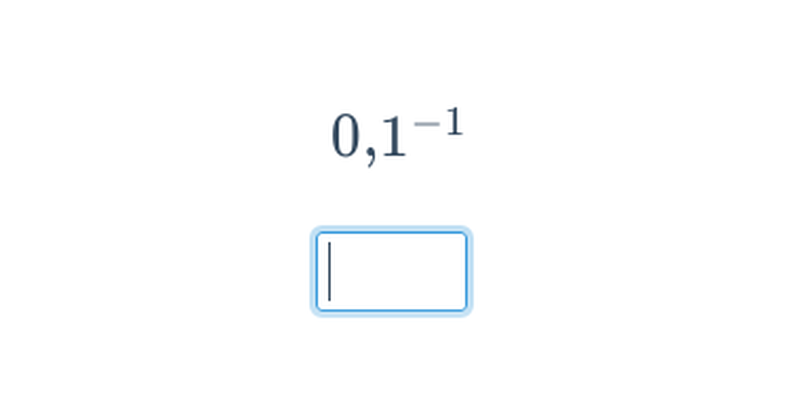
Umocňovanie je možné definovať aj pre záporný mocniteľ. Tento spôsob umocňovania sa využíva na vedecký zápis čísel, ktorý nám umožňuje prehľadne pracovať s veľmi veľkými alebo veľmi malými číslami, vďaka čomu má hojné využitie vo fyzike.
Umocňovanie a odmocňovanie môžeme prirodzene používať aj v spojitosti so zlomkami a desatinnými číslami.
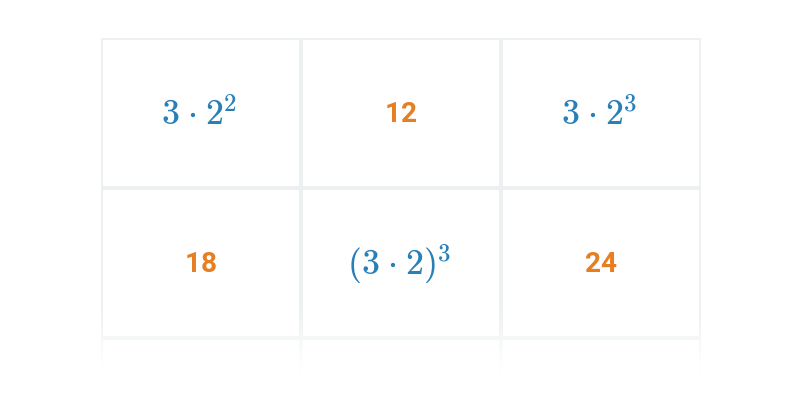
Presúvanie
Presúvanie kartičiek na správne miesto. Jednoduché ovládanie, zaujímavé a neotrepané úlohy.
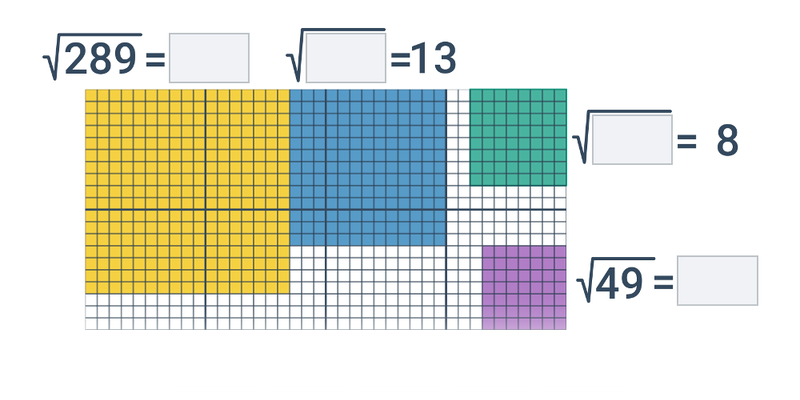
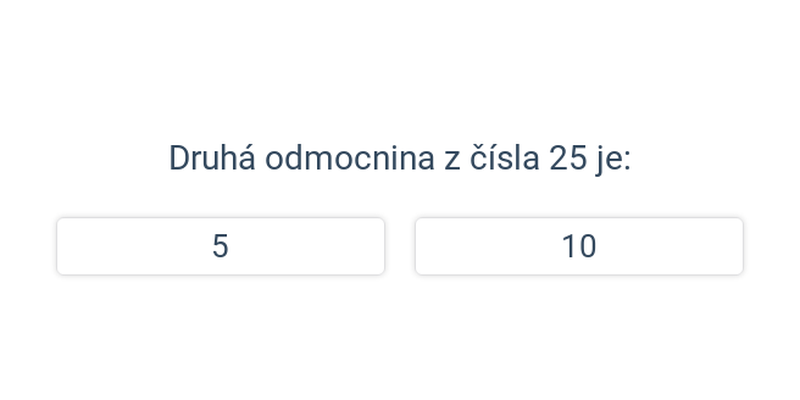
Rozhodovačka
Rýchle precvičovanie výberom z dvoch možností.
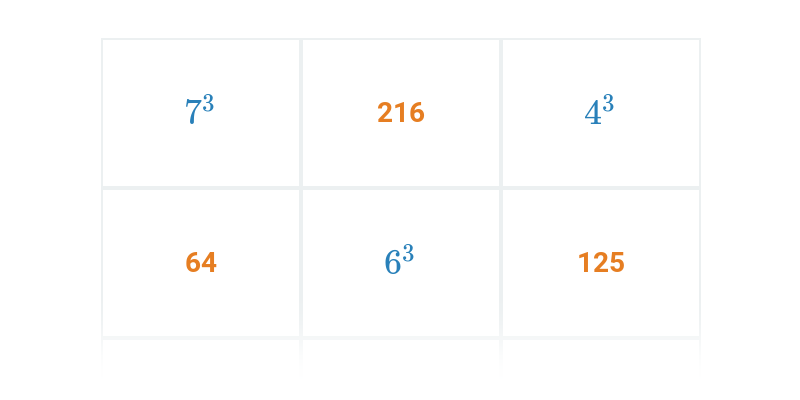
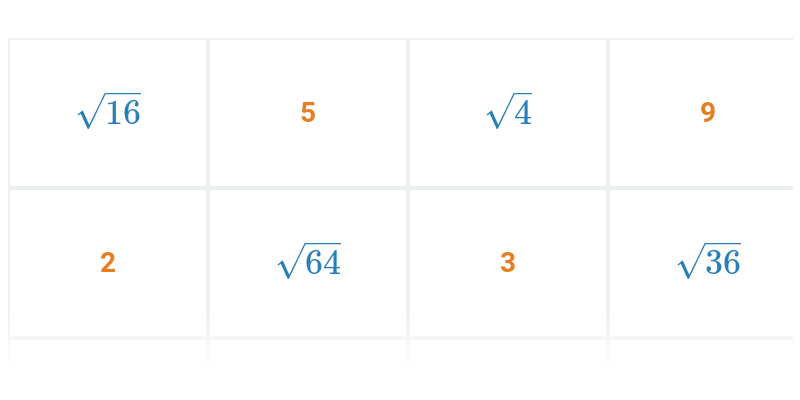
Pexeso
Hľadanie dvojíc, ktoré k sebe patria.
Krok za krokom
Doplňovanie jednotlivých krokov v rozsiahlejšom postupe.
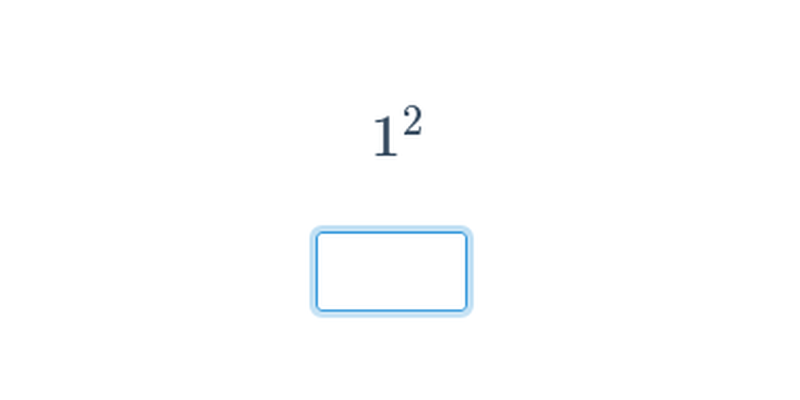
Počítanie
Cvičenie, v ktorom píšete odpoveď na klávesnici.
Kalkulačka
Úlohou je vyrobiť na displeji kalkulačky zadané čísla. Problém je, že jej chýbajú niektoré tlačidlá…