Záporné mocniny

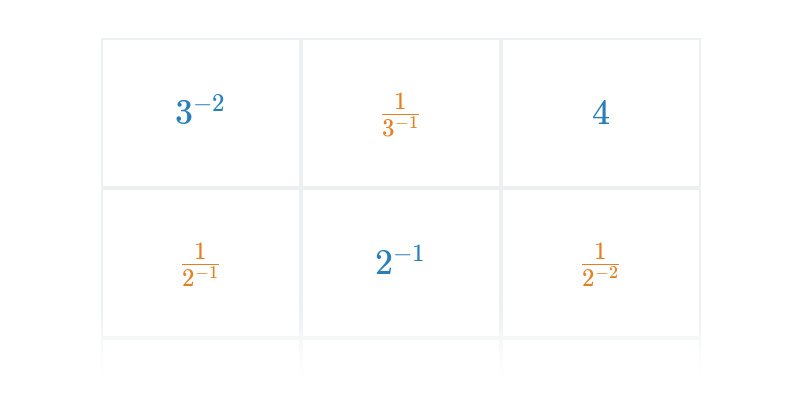
Mocnina so záporným exponentom zodpovedá prevrátenej hodnote príslušnej mocniny s kladným exponentom. Teda x^{-n} = \frac{1}{x^n}. Toto pravidlo je dôsledkom vlastnosti násobenia x^n\cdot x^m = x^{n+m}. Musí teda platiť x^{-n} \cdot x^n = x^{-n+n} = x^0 = 1.

Príklady:

• 2^{-1} = \frac{1}{2} = 0,5
• 2^{-2} = \frac{1}{2^2} = \frac{1}{4} = 0,25
• 10^{-2} = \frac{1}{10^2} = 0,01
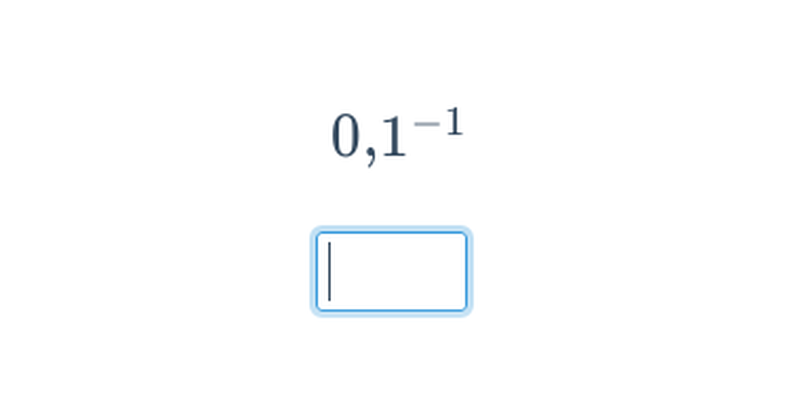
• 0,5^{-1} = 2^1 = 2