Obsah trojúholníka

Obsah trojuholníka vypočítame ako súčin dĺžky ľubovoľnej strany trojuholníka a výšky príslušnej k tejto strane, takže: S_{\triangle} = \frac12 \cdot a \cdot v_a = \frac12 \cdot b \cdot v_b = \frac12 \cdot c \cdot v_c

Čo si môžeme predstaviť ako polovicu obsahu obdĺžnika, v ktorom je náš trojuholník takto vpísaný:

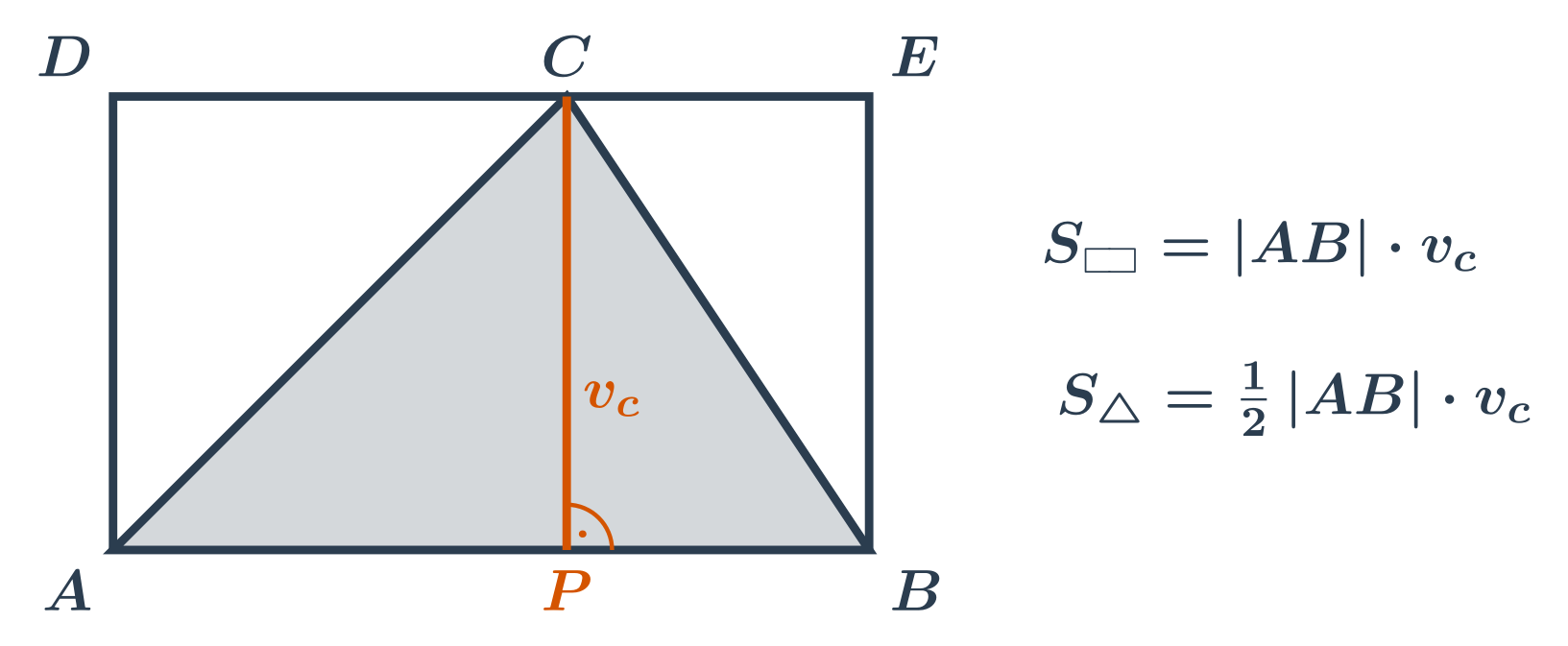
Príklady k obsahu:

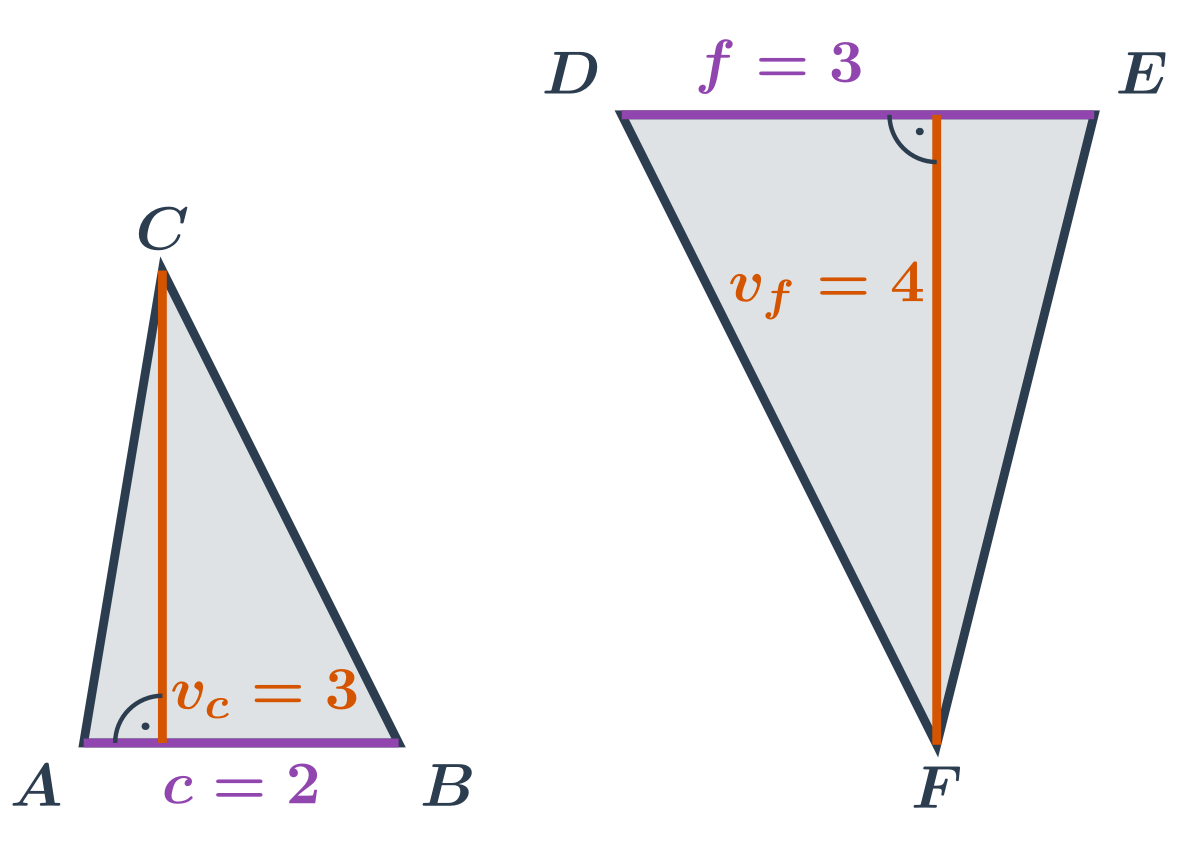
• Trojuholník ABC: Dĺžka strany \left| AB \right| je 2. Veľkosť k nej príslušnej výšky v_c je 3. Obsah trojuholníka ABC je rovný \frac12 \cdot 2 \cdot 3 = 3.
• Trojuholník DEF: Nevadí nám, že trojuholník na náčrtku vyzerá zvláštne natočený. Poznáme dĺžku strany \left| DE \right|, čo je 3. Veľkosť k nej príslušnej výšky v_f je 4. Obsah trojuholníka DEF je rovný \frac12 \cdot 3 \cdot 4 = 6.

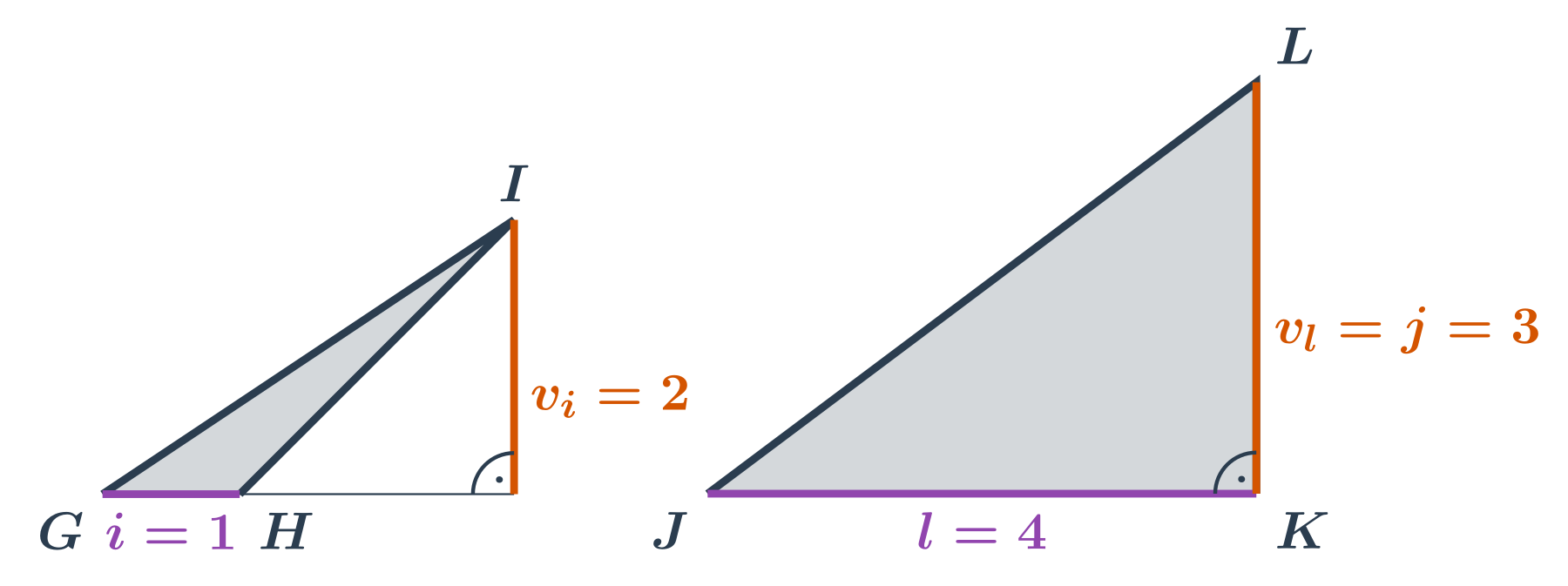
• Trojuholník GHI: Nevadí nám ani keď je päta kolmice, na ktorej leží výška, mimo stranu trojuholníka. Dĺžka strany \left| GH \right| je 1. Veľkosť k nej príslušnej výšky v_i je 2. Obsah trojuholníka GHI je \frac12 \cdot 2 \cdot 1 = 1.
• Trojuholník JKL: S pravouhlým trojuholníkom si tiež poradíme. Dĺžka strany \left| JK \right| je 4. Veľkosť k nej príslušnej výšky v_l je 3 (a je to zároveň aj dĺžka strany KL nášho trojuholníka). Obsah trojuholníka JKL je \frac12 \cdot 4 \cdot 3 = 6.