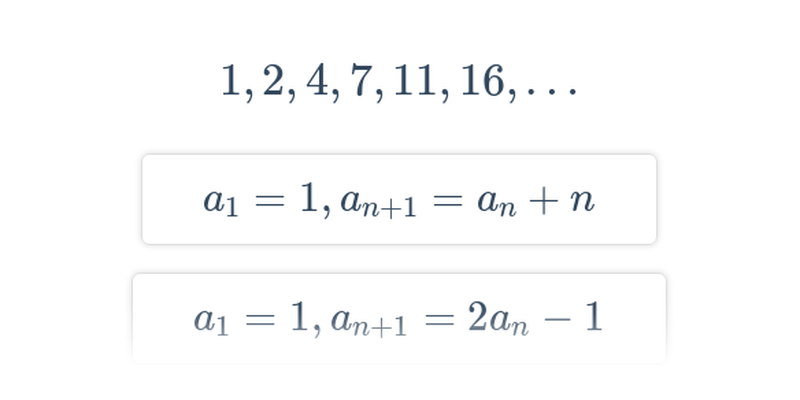Zápis postupností

Postupnosť je sada objektov, pri ktorých záleží na poradí a objekty sa môžu opakovať. Postupnosť môže byť konečná aj nekonečná. Členy postupnosti typicky zapisujeme pomocou indexov: a_n značí n-tý člen postupnosti a.

Postupnosti môžeme zapísať rôznymi spôsobmi:

• vymenovaním členov: a = (7, 10, 13, 16, 19, 22)
• vzorcom pre n-tý člen: a_n = 4 + 3\cdot n
• rekurentne (začiatok postupnosti a spôsob výpočtu ďalších členov z predchádzajúcich): a_1 = 7, a_n = a_{n-1} + 3

Príklady:

• 8, 18, 28, 38, 48, 58, … (aritmetická postupnosť s počiatočnou hodnotou 8 a diferenciou 10)
• 3, 6, 12, 24, 48, 96, … (geometrická postupnosť s počiatočnou hodnotou 3 a kvocientom 2)
• 1, 1, 2, 3, 5, 8, 13, 21, 34, … (Fibonacciho postupnosť, a_n = a_{n-1} + a_{n-2})
• 1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, 2, … (periodická postupnosť)

Existuje celý rad zaujímavých postupností. Majú dokonca svoju vlastnú encyklopédiu.