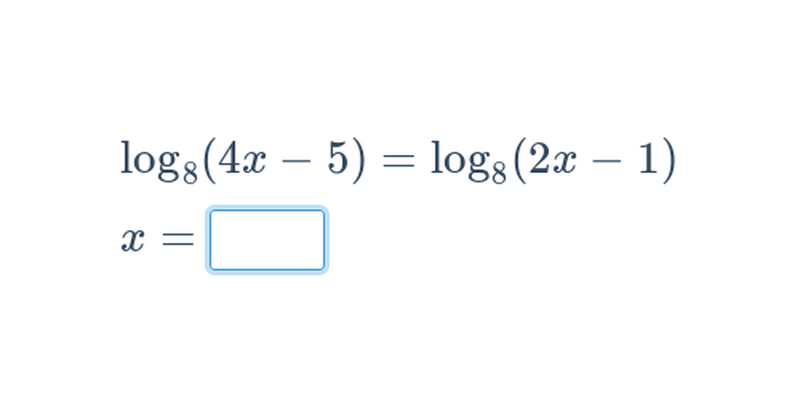Logaritmické rovnice

Logaritmická rovnica je taká, kde neznáma vystupuje ako argument logaritmickej funkcie, napr. 2 \cdot \log_6(x-2) = \log_6(14-x).

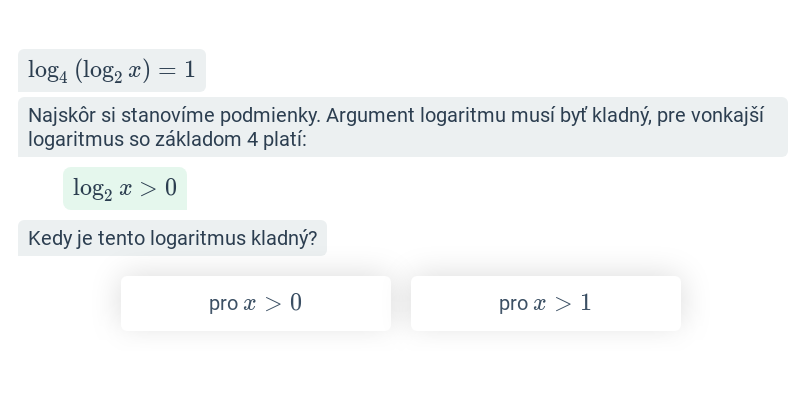
Pri logaritmických rovniciach si musíme dávať pozor na podmienky riešenia. Argument každého logaritmu totiž musí byť vždy kladné číslo. V uvedenom príklade teda musí platiť x-2>0 a súčasne 14-x > 0.

Logaritmické rovnice riešime s využitím vlastností logaritmickej funkcie a jej vzťahu k exponenciálnej funkcii. Čiastkové spôsoby, ako riešiť logaritmické rovnice:

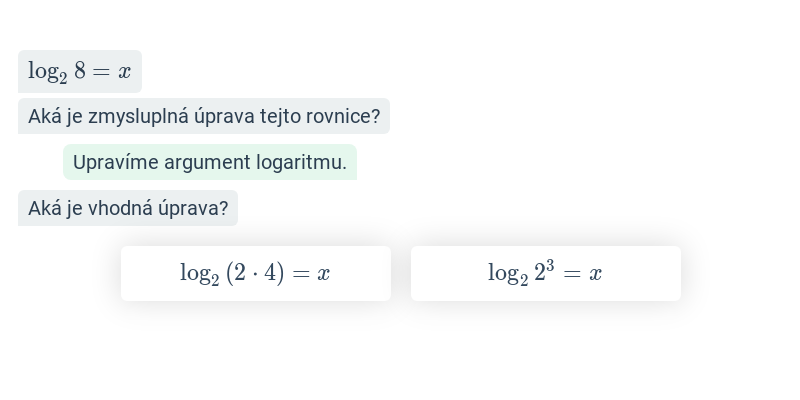
• Prevedieme rovnicu na tvar \log_a f(x) = c. Potom musí platiť f(x) = a^c.
• Prevedieme rovnicu na tvar \log_a f(x) = \log_a g(x). Potom musí platiť f(x) = g(x).