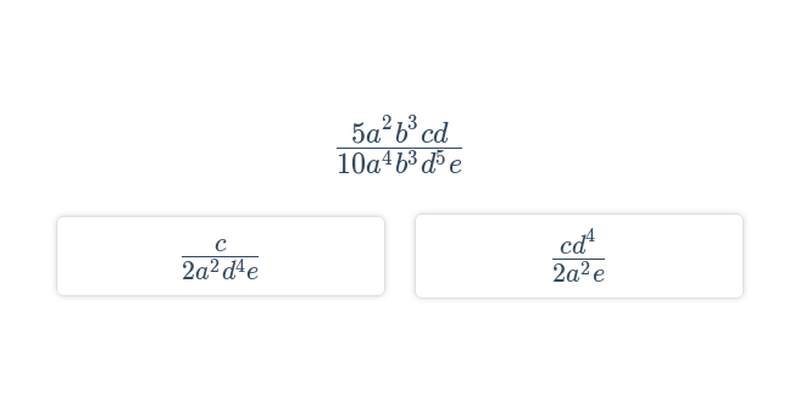
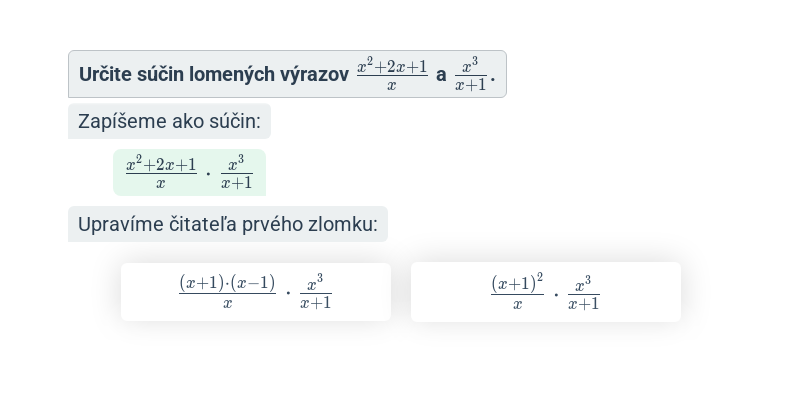
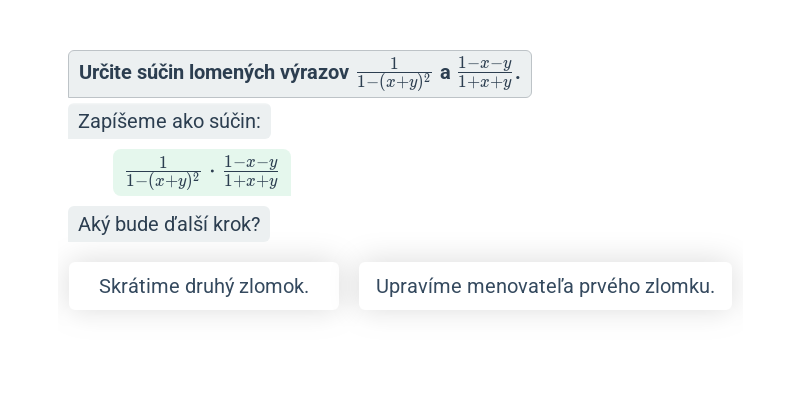
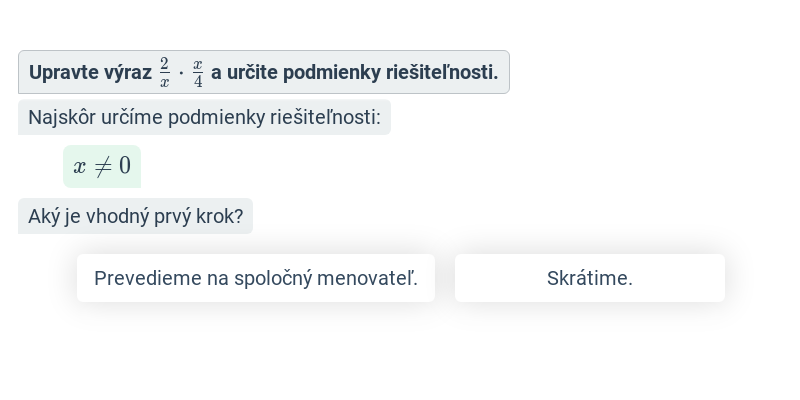
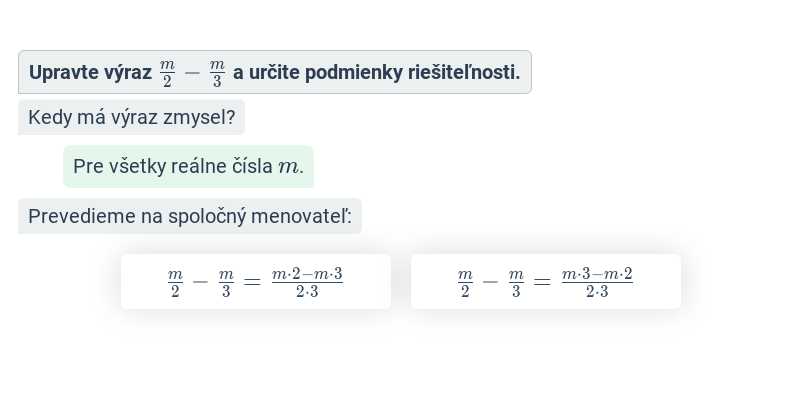
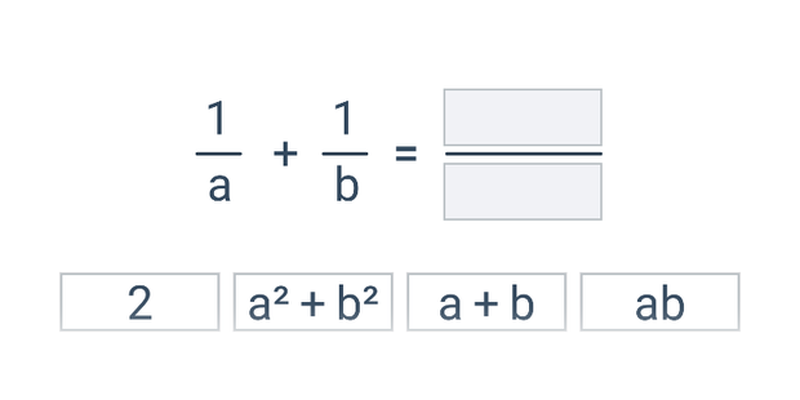Lomený výraz má tvar zlomku, v menovateli ktorého je mnohočlen (výraz s premennou). Príkladom lomeného výrazu je \frac{x+2}{x^2-1}. S lomenými výrazmi počítame podobne ako so zlomkami.
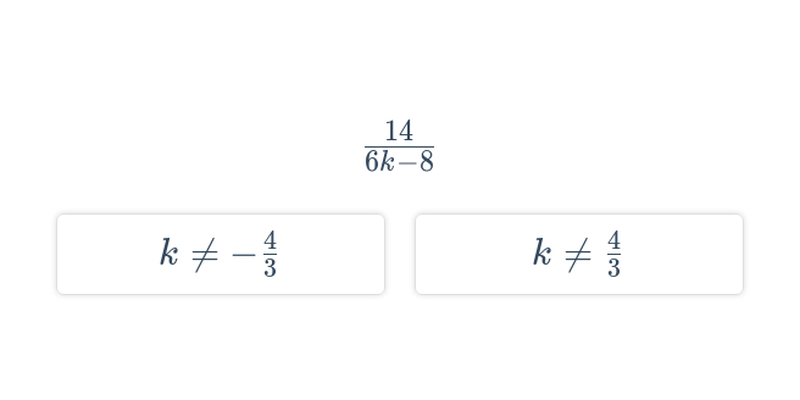
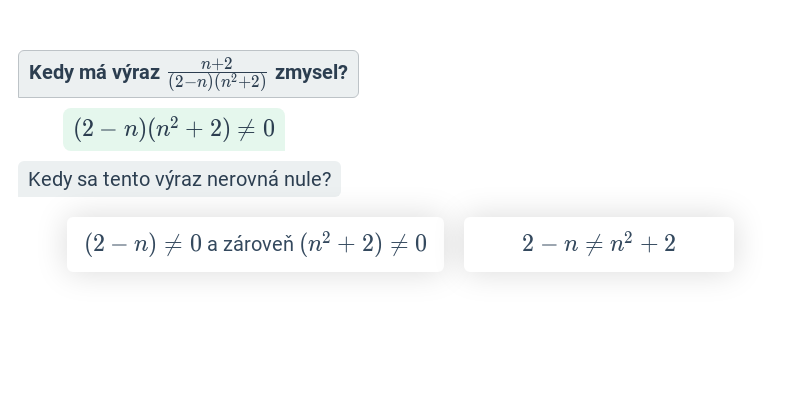
Pri lomených výrazoch je treba brať do úvahy podmienky, za ktorých majú zmysel. Lomený výraz má zmysel pre všetky hodnoty premenných, pre ktoré je výraz v menovateli iný než nula. Príklady:
- Výraz \frac{x+5}{x-3} má zmysel pre x \neq 3.
- Výraz \frac{x^3}{x^2-1} má zmysel pre x \in \mathbb{R} \setminus \{-1, 1\}, pretože x^2-1 = 0 pre hodnoty -1 a 1.
- Výraz \frac{x^3}{x^2+1} má zmysel pre všetky reálne čísla, pretože x^2+1 je vždy väčšie ako nula.
Presúvanie
Presúvanie kartičiek na správne miesto. Jednoduché ovládanie, zaujímavé a neotrepané úlohy.
Rozhodovačka
Rýchle precvičovanie výberom z dvoch možností.
Krok za krokom
Doplňovanie jednotlivých krokov v rozsiahlejšom postupe.
Počítanie
Cvičenie, v ktorom píšete odpoveď na klávesnici.