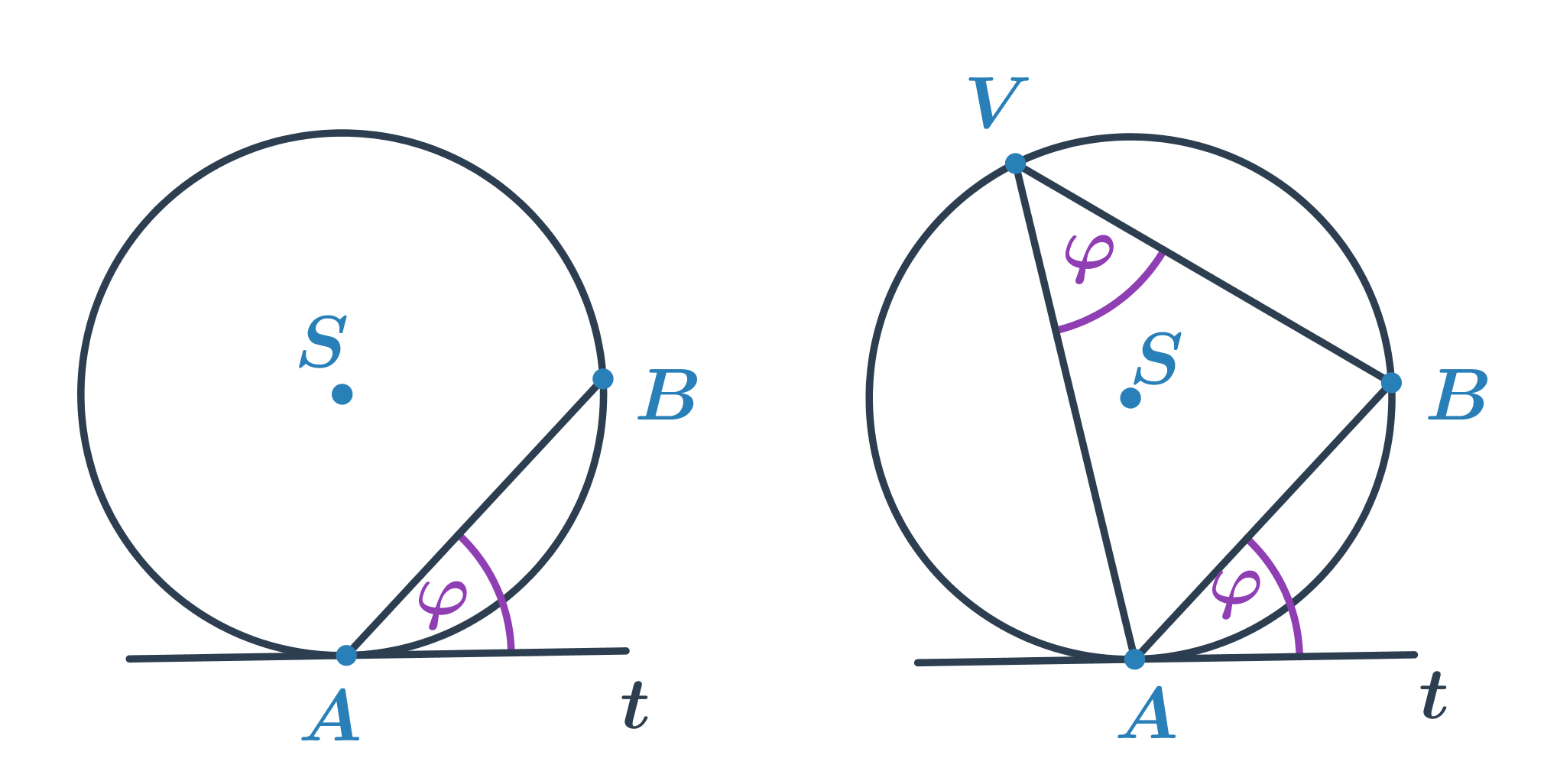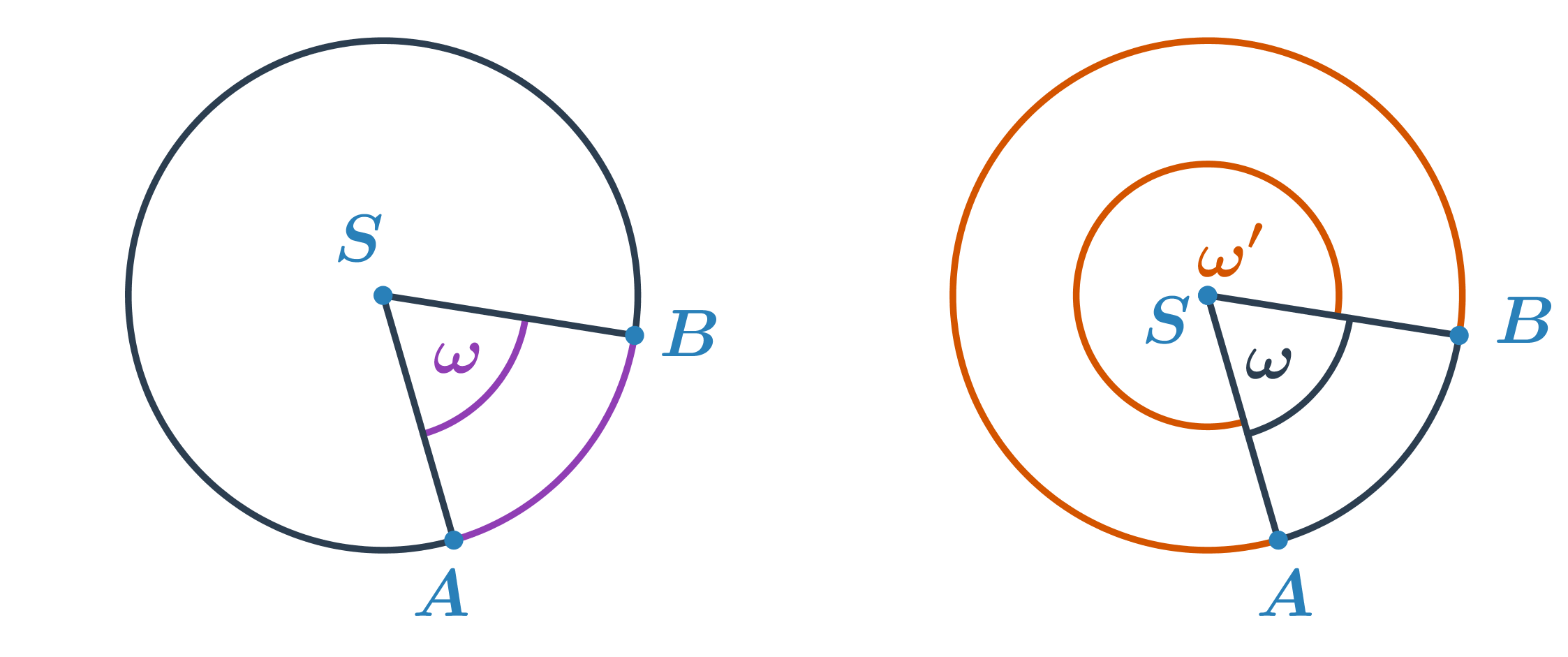
Stredový uhol

• Uhol s vrcholom v strede S kružnice k, ktorého ramená prechádzajú krajnými bodmi A, B oblúka kružnice k.
• Pre každé dva body na kružnici je možné určiť dva stredové uhly. Každý prináleží tomu oblúku, ktorý v danom uhle leží.

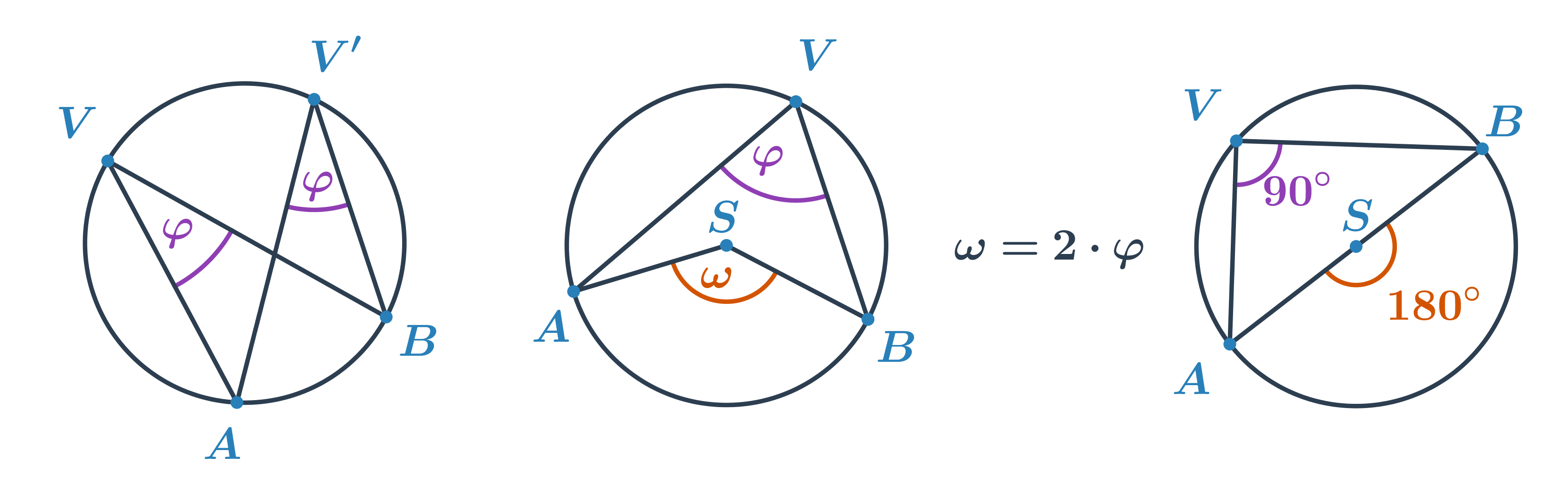
Obvodový uhol

• Uhol, ktorého vrchol V leží na kružnici k a jeho ramená prechádzajú bodmi A, B oblúka kružnice k (A \neq V \neq B)
• Všetky obvodové uhly prináležiace oblúku AB s vrcholom V, ktorý na oblúku neleží, majú rovnakú veľkosť.
• Veľkosť stredového uhla \omega sa rovná dvojnásobku veľkosti obvodového uhla \varphi príslušného k rovnakému oblúku, \omega = 2\cdot\varphi.
• Tálesova veta: Obvodový uhol nad priemerom kružnice je pravý.

Úsekový uhol

• Uhol, ktorý zviera tetiva AB kružnice k s dotyčnicou t kružnice v bode A alebo B.
• Veľkosť úsekového uhla je rovnaká ako veľkosť obvodového uhla nad oblúkom AB.

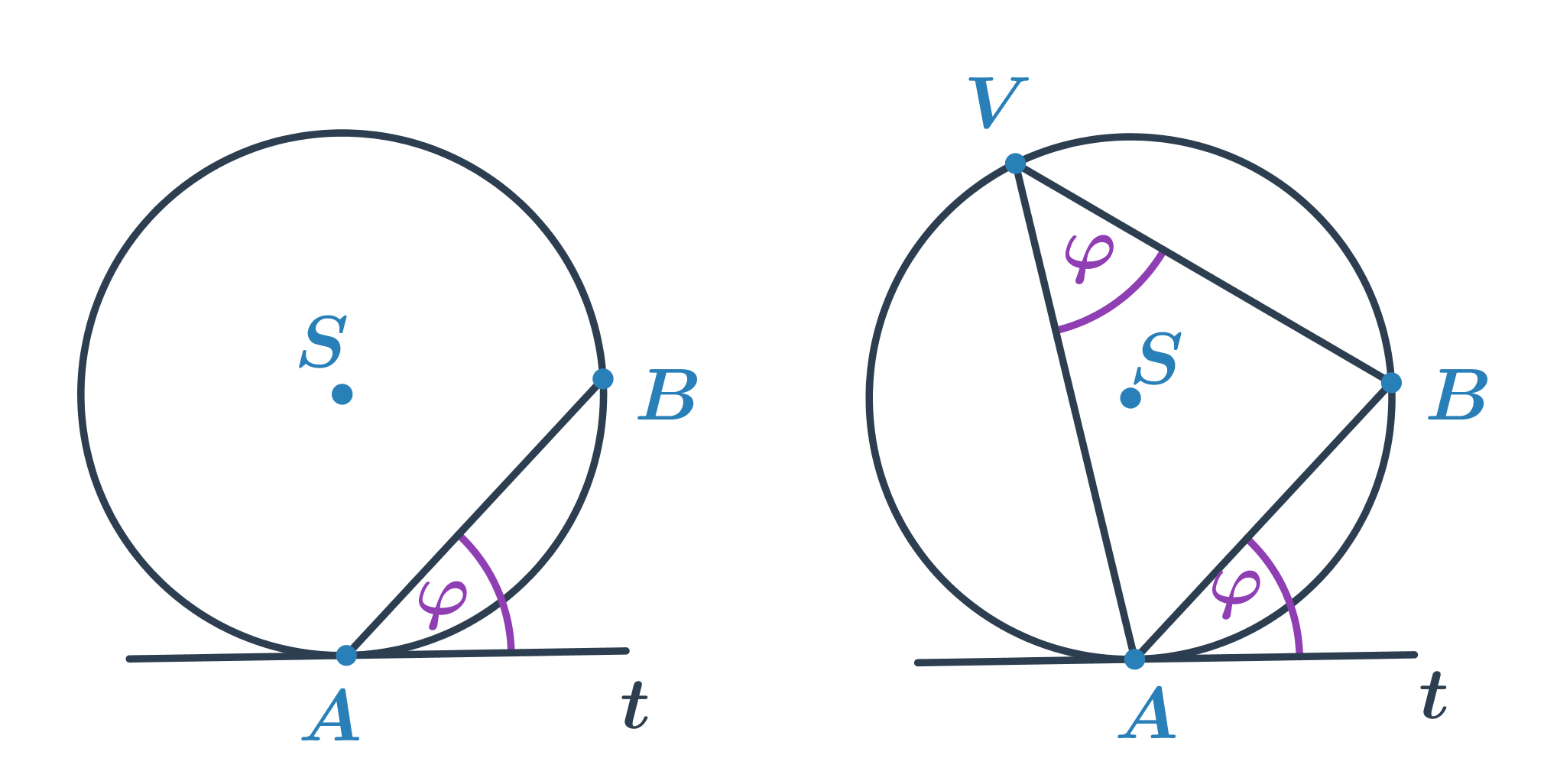
Príklad 1: Určite veľkosť oranžového uhla.

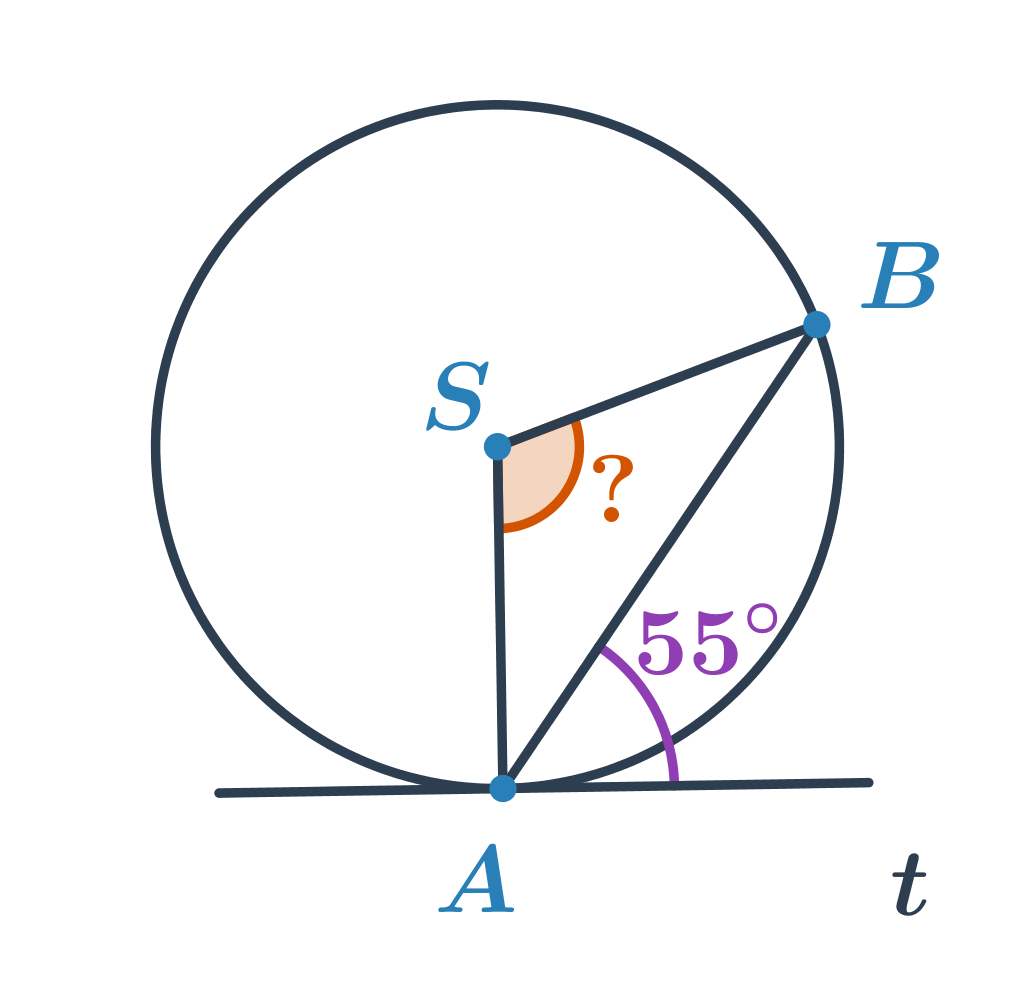
Uhol s veľkosťou 55^\circ je úsekový uhol prináležiaci tetive AB. Vieme, že veľkosti úsekového a príslušného obvodového uhla sú rovnaké, teda 55^\circ. Neznámy uhol je stredový uhol prináležiaci menšiemu oblúku AB. Jeho veľkosť je dvojnásobkom veľkosti obvodového uhla, teda 2\cdot55^\circ=110^\circ.

Príklad 2: Určite veľkosť oranžového uhla.

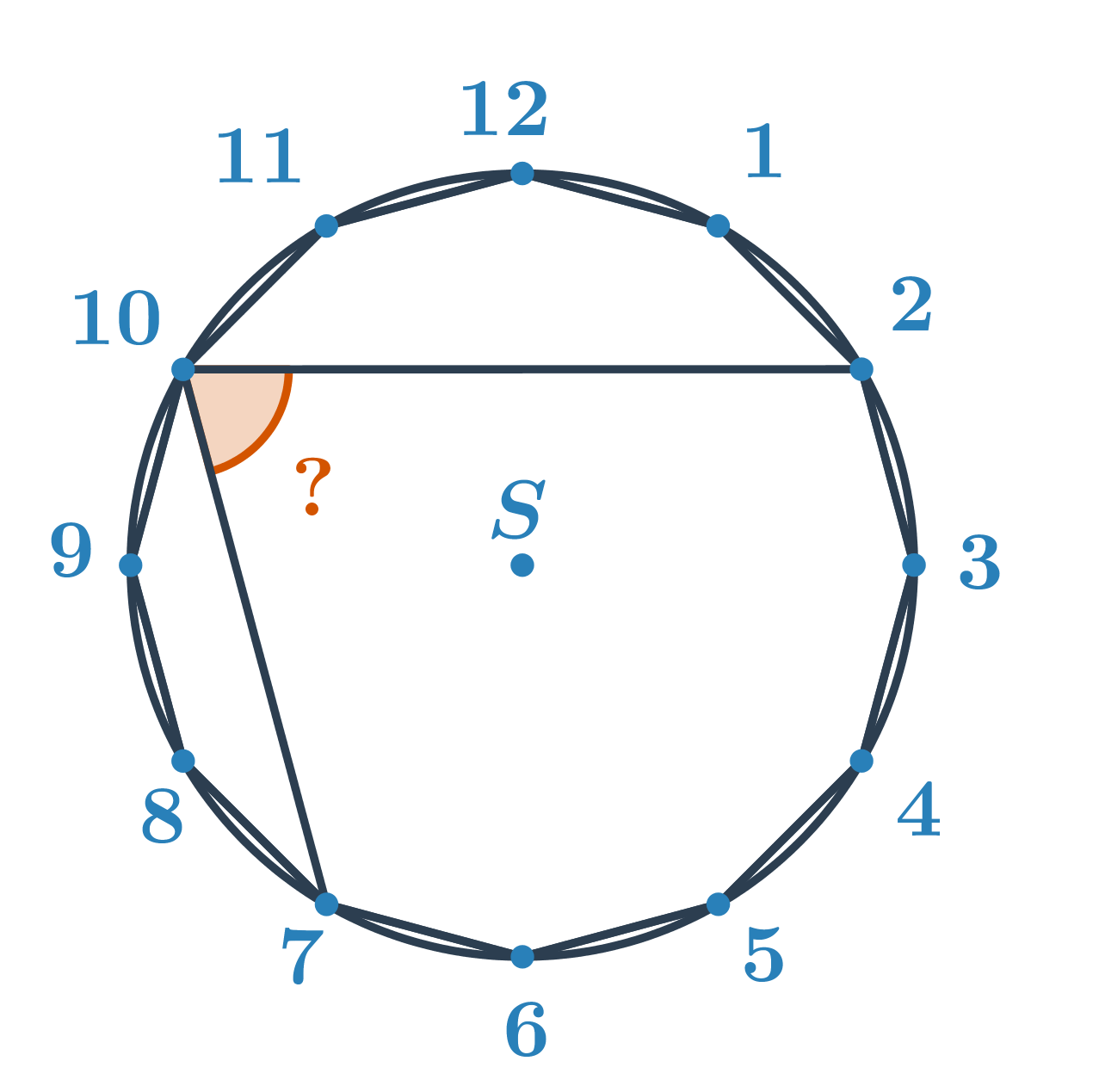
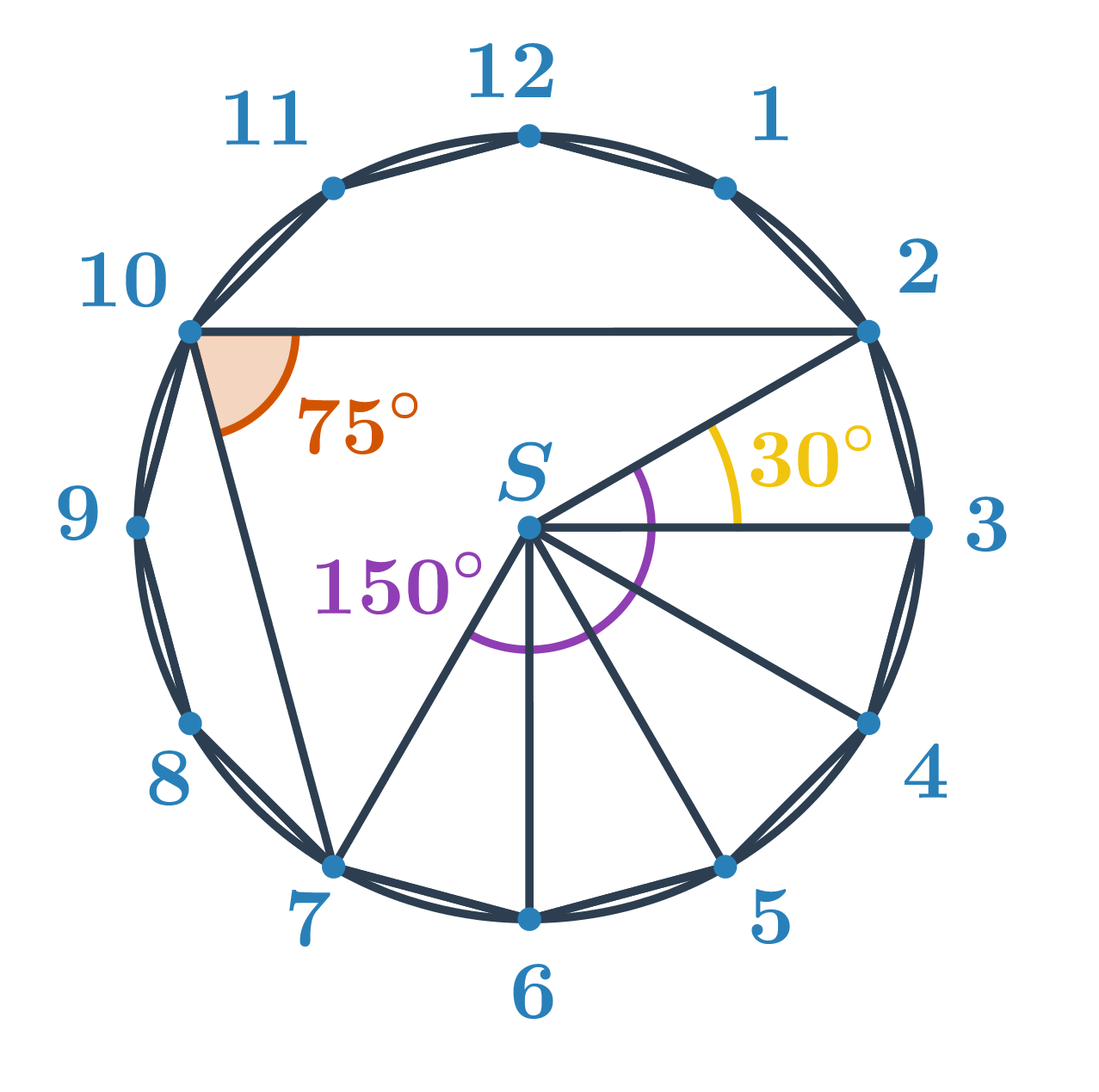
Neznámy uhol je obvodovým uhlom nad menším oblúkom s koncovými bodmi 2 a 7. Určíme veľkosť príslušného stredového uhla. Z kapitoly uhly a mnohouholníky vieme, že veľkosť stredového uhla pravidelného n-uholníka je \frac{360^\circ}{n}. Pre pravidelný dvanásťuholník je teda uhol medzi spojnicami dvoch vedľajších vrcholov a stredu \frac{360^\circ}{12}=30^\circ. Stredový uhol príslušný oblúku 2 a 7 je potom 5\cdot30^\circ=150^\circ. Hľadaný obvodový uhol má polovičnú veľkosť, teda 150^\circ:2=75^\circ.