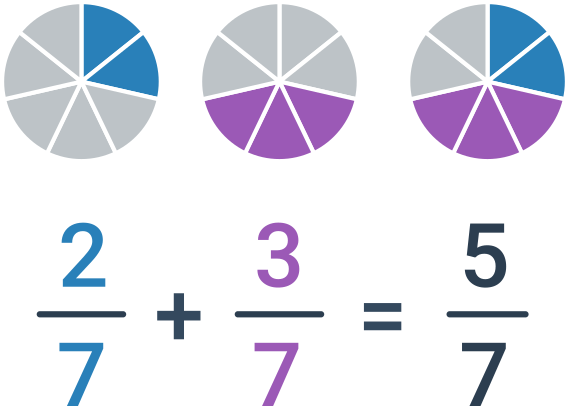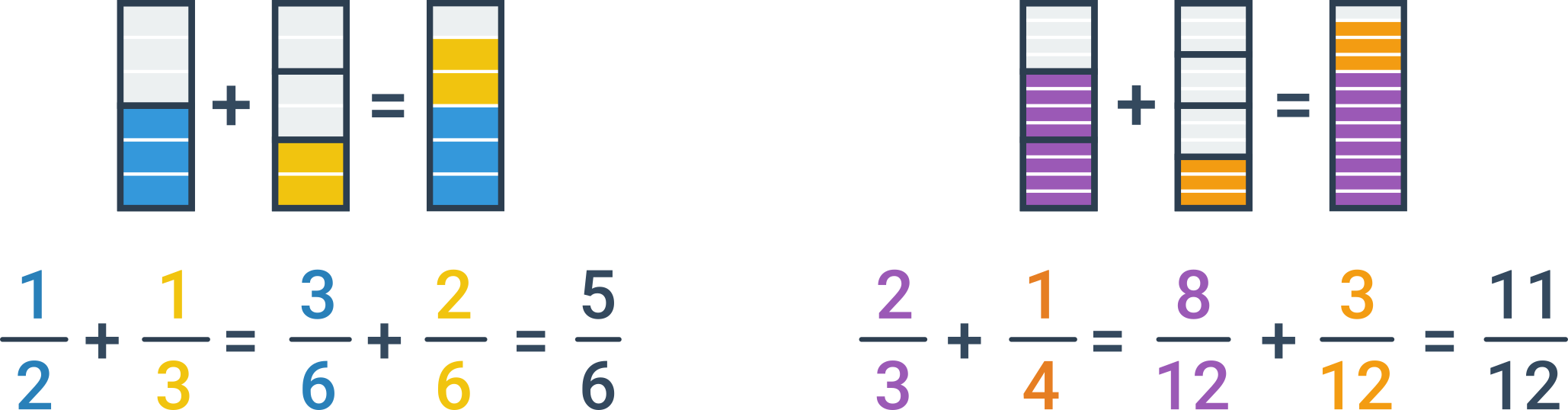Sčítanie a odčítanie zlomkov

Než sa pustíme do sčítania zlomkov, je dobré mať jasno v tom, čo je čitateľ („to hore“) a menovateľ („to dole“). V zlomku \frac{3}{7} je 3 čitateľ, 7 menovateľ.
Sčítanie zlomkov s rovnakým menovateľom
Ak majú sčítané zlomky rovnaké menovatele, stačí jednoducho sčítať čitatele. Menovateľ necháme rovnaký, teda \frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}.
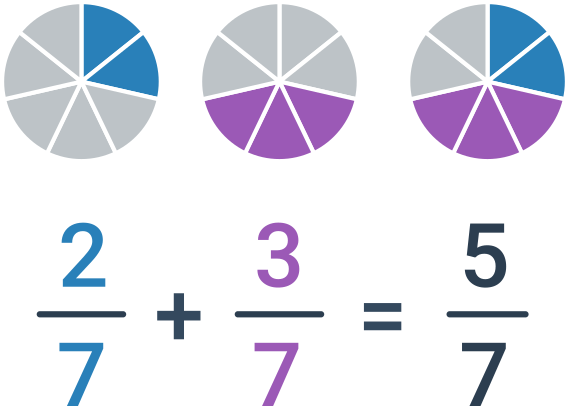
Sčítanie zlomkov s rôznymi menovateľmi
Ak majú sčítané zlomky rôzne menovatele, musíme ich najskôr rozšíriť tak, aby mali rovnaký menovateľ. Najvýhodnejšie je rozšíriť zlomky na najmenší spoločný násobok pôvodných menovateľov. Keď už majú zlomky rovnaký menovateľ, sčítame ich vyššie uvedeným postupom.
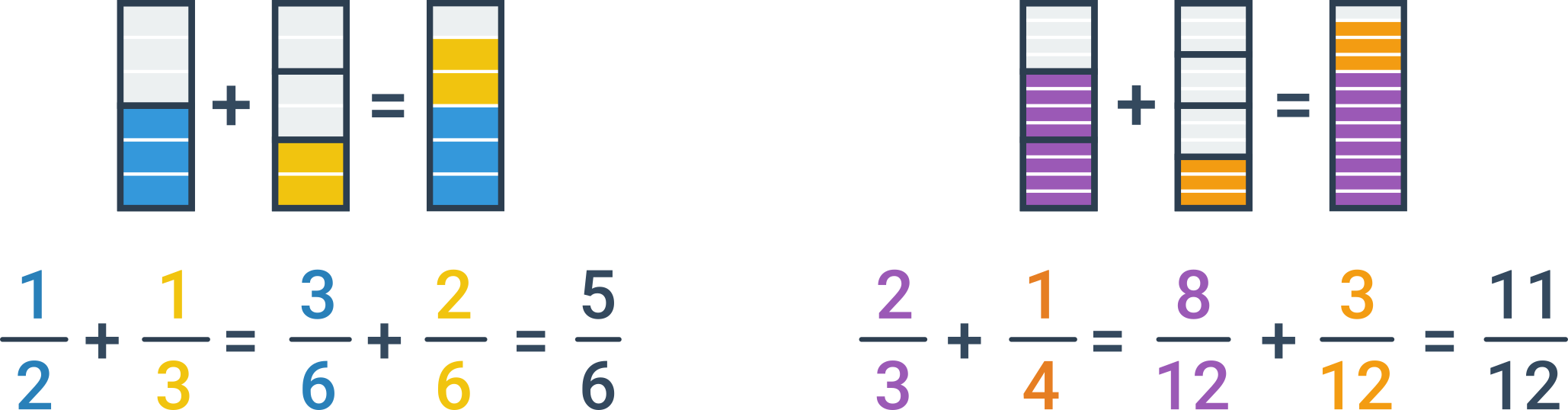
Úpravy a odčítanie
Výsledný zlomok väčšinou ešte krátime, aby sme dostali výsledok v základnom tvare. Odčítanie zlomkov funguje rovnakým spôsobom.
Príklady
Príklad s rovnakým menovateľom, bez nutnosti krátenia:
\frac{2}{5}+\frac{1}{5} = \frac{2+1}{5} = \frac{3}{5}.
Príklad s rovnakým menovateľom, kedy výsledok krátime:
\frac{5}{6}-\frac{1}{6} = \frac{5-1}{6} = \frac{4}{6} = \frac{2}{3}.
Príklad s rôznymi menovateľmi: \frac{5}{6} - \frac{3}{4}. Najmenší spoločný násobok menovateľov 6 a 4 je 12, rozšírime teda zlomky na menovateľ 12:
\frac{5}{6} - \frac{3}{4} = \frac{5\cdot 2}{6\cdot 2} - \frac{3\cdot 3}{4\cdot 3}= \frac{10}{12} - \frac{9}{12} = \frac{1}{12}
Zatvoriť