
Elipsa

Elipsa je množina všetkých bodov v rovine, ktoré majú od dvoch rôznych bodov (ohnísk) stály súčet vzdialeností 2a, ktorý je väčší než vzdialenosť ohnísk.
Stredová rovnica elipsy
Tvar stredovej rovnice elipsy so stredom S[m;n] s veľkosťami hlavnej a vedľajšej polosi a a b závisí od polohy hlavnej osi:
hlavná os je rovnobežná s osou x, rovnica je v tvare: \frac{(x-m)^2}{a^2} +\frac{(y-n)^2}{b^2}=1 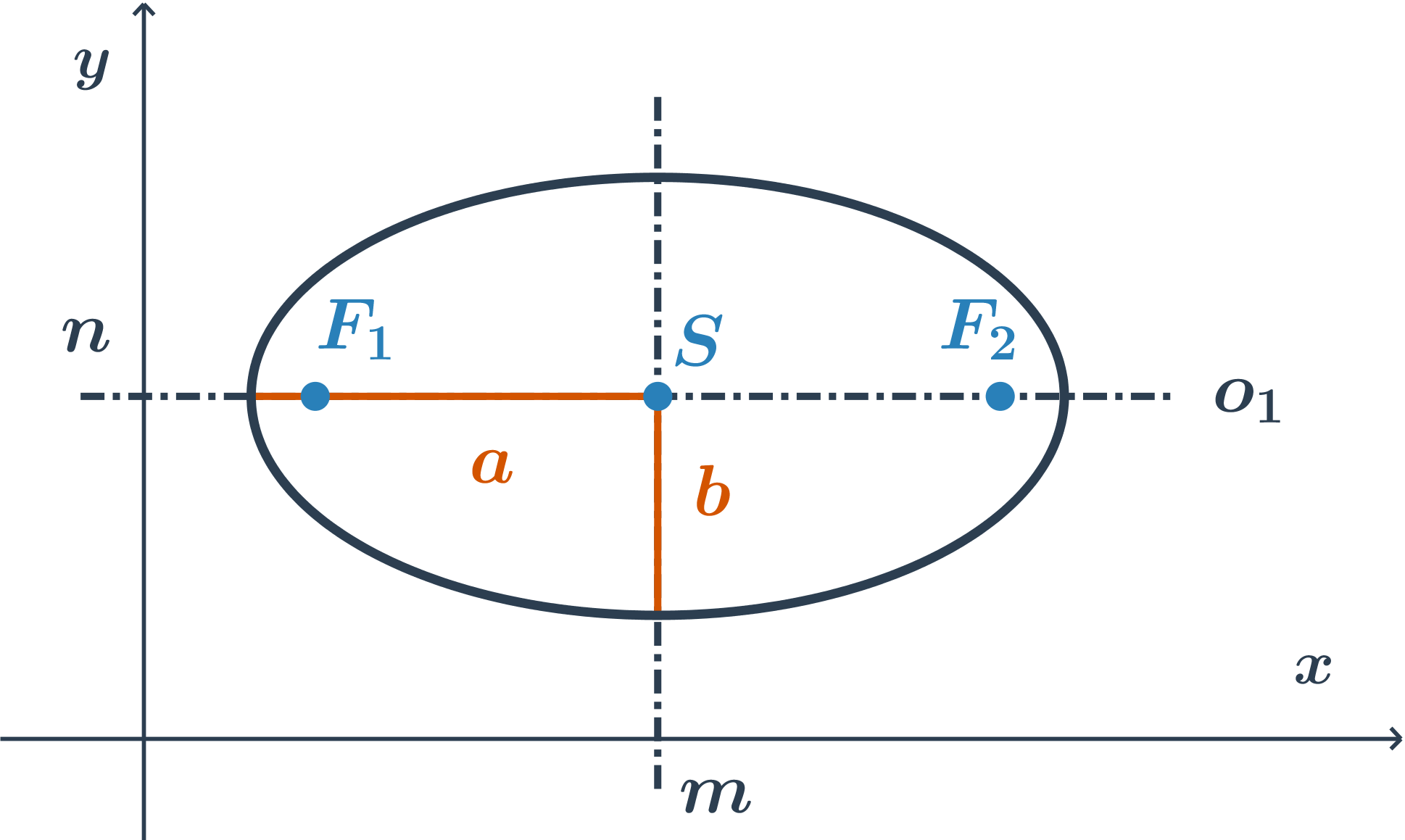
hlavná os je rovnobežná s osou y, rovnica je v tvare: \frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1 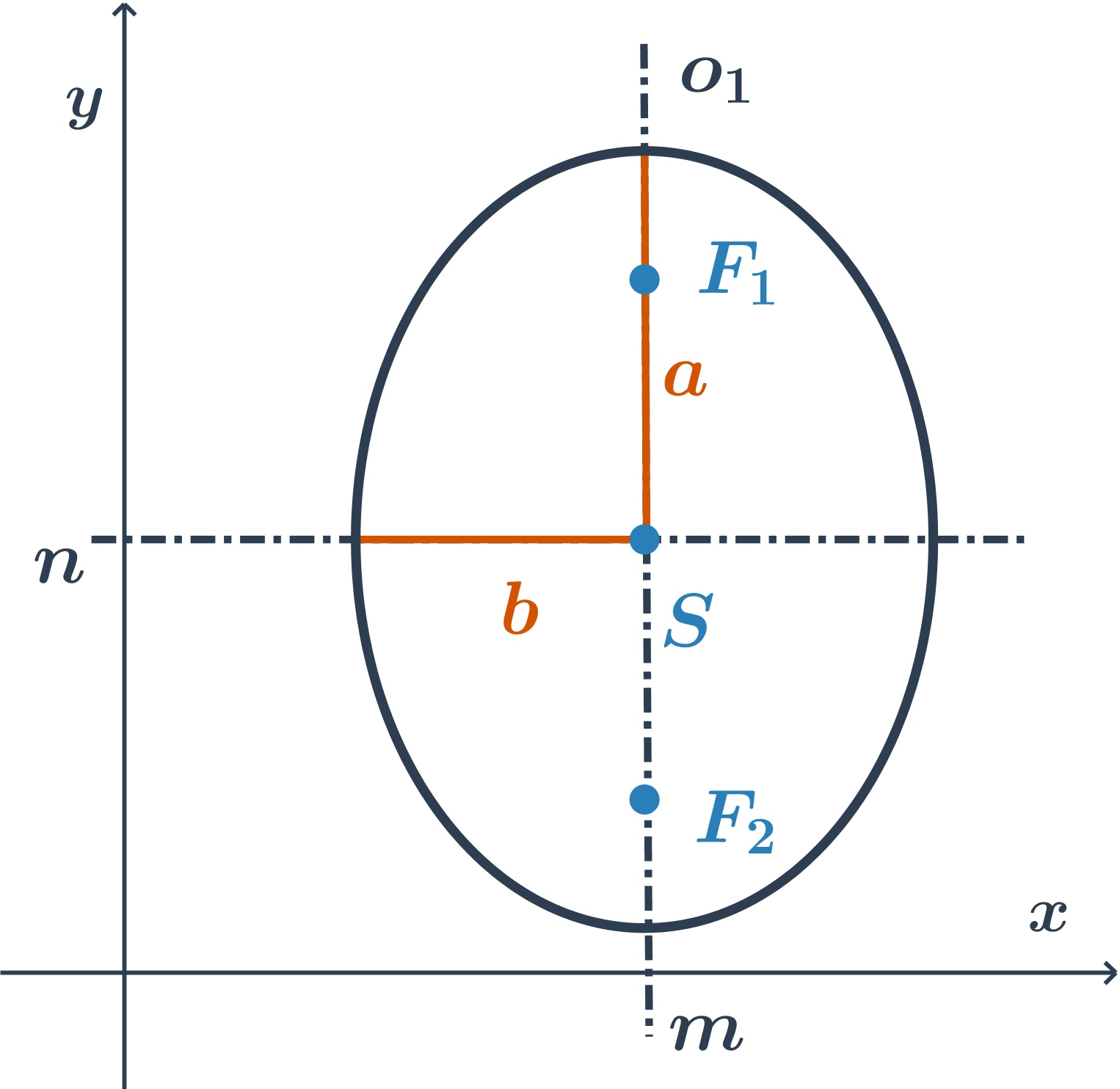
Návod: ako z rovnice zistiť, s ktorou súradnicovou osou je rovnobežná hlavná os elipsy
- Pozrieme sa do menovateľov.
- Väčší menovateľ je druhá mocnina veľkosti hlavnej polosi (a menší menovateľ je druhá mocnina veľkosti vedľajšej polosi).
- Premenná v danom čitateli (zlomku s väčším menovateľom) potom určuje, s ktorou osou je hlavná os elipsy rovnobežná.
- Stručne povedané: ak je väčšie číslo napríklad v menovateli s premennou x, je hlavná os rovnobežná s osou x.
Príklad: určenie stredovej rovnice elipsy s daným stredom, veľkosťami polosí a smerom hlavnej osi
Určite stredovú rovnicu elipsy so stredom v bode S[-2;3], je‑li a=3, b=2 ak hlavná os je rovnobežná s osou y.
- Stredová rovnica je v tvare \frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1.
- Dosadíme súradnice stredu a veľkosti hlavnej a vedľajšej polosi. Pri dosadení si dáme pozor na to, že súradnice stredu odčítame: \frac{(x-(-2))^2}{2^2} +\frac{(y-3)^2}{3^2}=1
- Po úprave: \frac{(x+2)^2}{4} +\frac{(y-3)^2}{9}=1
Všeobecná rovnica elipsy
Podobne ako existuje niekoľko rovníc priamky, môžeme aj rovnicu elipsy zapísať iným spôsobom. Všeobecná rovnica elipsy je v tvare:
Ax^2 +By^2+Cx+Dy+E=1, A\ne B, A\cdot B>0.
Každá rovnica v tomto tvare ale nemusí byť všeobecnou rovnicou elipsy. Praktické overenie, či ide o elipsu vykonávame prevedením na stredovú rovnicu.
Príklad: určuje daná rovnica elipsu?
Rozhodnite, či rovnica x^2+3y^2+8x-18y+31=0 určuje elipsu.
- Najskôr si usporiadame členy: x^2+8x+3y^2-18y+31=0.
- Z členov s premennou y vytkneme 3: x^2+8x+3(y^2-6y)+31=0
- K obom stranám rovnice pripočítame konštanty 16 a 27, aby sme členy s premennými x a y mohli upraviť podľa vzťahu (a\pm b)^2=a^2 \pm 2ab +b^2.
- Máme: x^2+8x+16+3(y^2-6y+9)+31=16+27
- A upravíme: (x+4)^2 +3(y-3)^2+31=43
- Prevedieme konštantu 31 na druhú stranu rovnice: (x+4)^2 +3(y-3)^2=12
- Na záver rovnicu vydelíme 12: \frac{(x+4)^2}{12} +\frac{(y-3)^2}{4}=1
- Ide teda o elipsu.
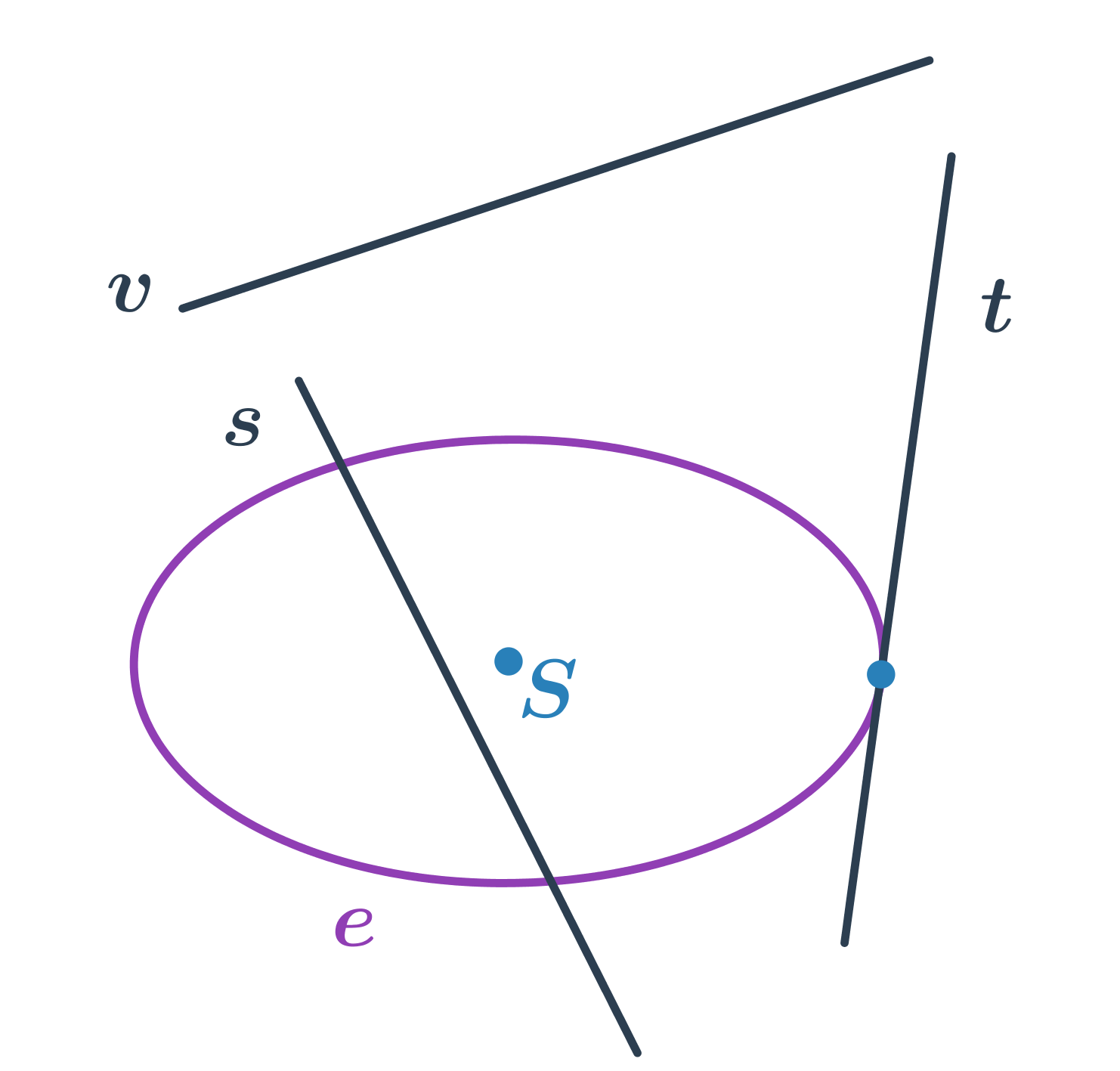
Elipsa a priamka
- priamka s pretína elipsu v dvoch bodoch – sečnica elipsy
- priamka t pretína elipsu v jednom bode – dotyčnica elipsy
- priamka v elipsu nepretína – vonkajšia priamka elipsy
Rovnice dotyčnice elipsy v bode, ktorý leží na elipse
Elipsa daná rovnicou \frac{(x-m)^2}{a^2} +\frac{(y-n)^2}{b^2}=1 má v bode T[x_0;y_0] dotyčnicu určenú rovnicou:
\frac{(x-m)(x_0-m)}{a^2} +\frac{(y-n)(y_0-n)}{b^2}=1
Podobne môžeme zapísať aj rovnicu dotyčnice elipsy, ktorá má hlavnú os rovnobežnú s osou y.
Príklad: určenie rovnice dotyčnice elipsy v jej danom bode
Určite rovnicu dotyčnice elipsy \frac{(x-2)^2}{9} +\frac{(y-2)^2}{18}=1 v jej bode T[1;-2].
- Overíme, či bod T leží na elipse: \frac{(1-2)^2}{9} +\frac{(-2-2)^2}{18}=1 \Rightarrow \frac19+\frac{16}{18}=1 \Rightarrow 1=1
- Dotyčnica má rovnicu \frac{(x-m)(x_0-m)}{b^2} +\frac{(y-n)(y_0-n)}{a^2}=1
- Dosadíme súradnice bodu T: \frac{(x-2)(1-2)}{9} +\frac{(y-2)(-2-2)}{18}=1
- Zbavíme sa zlomkov: 2(x-2)\cdot(-1) +(y-2)\cdot(-4)=18
- Roznásobíme zátvorky: -2x+4 -4y+8=18
- A dostaneme všeobecnú rovnicu dotyčnice: x+2y+3=0
Zatvoriť














