Slovenčina
Angličtina
Informatika
Vieme to
Nemčina
Biológia
Zemepis
Chémia
Fyzika
Aritmetika
Zlomky, percentá, desatinné čísla
Geometria
Elementárna algebra
Funkcie
Jednotky, miery
Diskrétna matematika
Finančná gramotnosť
Rozhodovačka
Pexeso
Krok za krokom
Počítanie
Grafár
Porozumenie
Označovanie
Presúvanie
Mriežkovaná
Rozdeľovačka
Pokazená kalkulačka
Roboti
Strieľačka
Príšerky
Preteky
Územia
Tipovačka
Tímovka
Môj účet
Odhlásiť sa
Rozhodovačka
Analytická geometria
Precvičujte neobmedzeneVáš denný počet odpovedí je obmedzený. Pre navýšenie limitu alebo prístup do svojho účtu s licenciou sa prihláste.
Prihlásiť sa
GS4
QR kód
Kód / krátka adresa
Skopírujte kliknutím.
Nastavenie cvičení
Pozor, nastavenie je platné iba pre toto cvičenie a predmet.
Priamky: pojmy
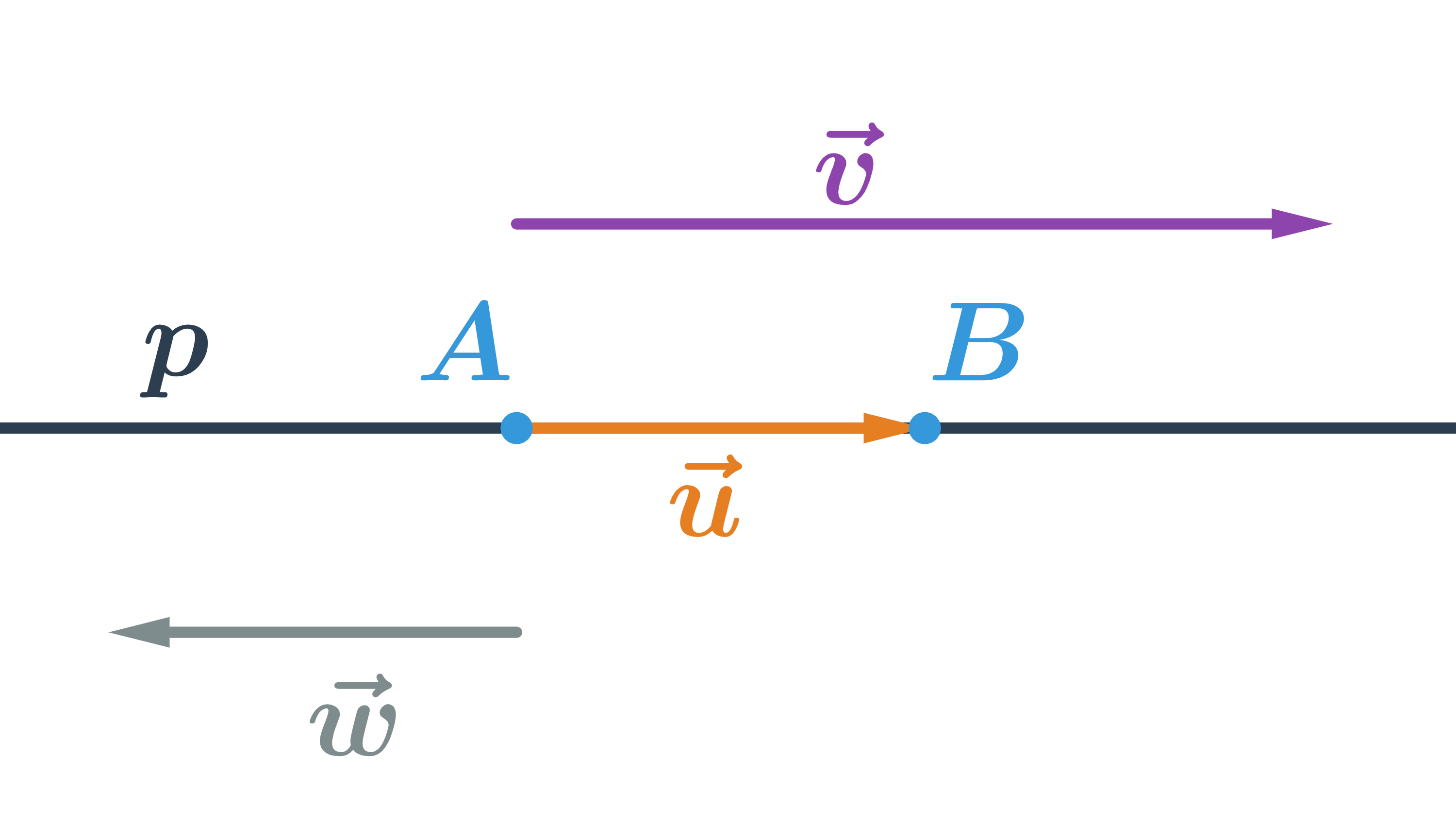
Priamka je jednoznačne určená dvomi bodmi, na obrázku je priamka p určená bodmi A a B. Každý vektor, ktorý je rovnobežný s vektorom \overrightarrow{AB} sa nazýva smerový vektor priamky p. Ktorýkoľvek z vektorov na obrázku je smerový vektor priamky p. K tomu, aby sme určili konkrétnu priamku ešte potrebujeme poznať jeden bod na priamke (priamka p na obrázku je určená bodom A a ktorýmkoľvek z vektorov \vec{u}, \vec{v}, \vec{w}).
Parametrické rovnice priamky
Priamka určená bodom A=[a_1;a_2] a vektorom \vec{u}=(u_1;u_2) má parametrické rovnice tvaru: \begin{array}{rrl}x&=&a_1+t\cdot u_1\\y&=&a_2+t\cdot u_2\\&&t\in\mathbb{R}\end{array} Skrátene môžeme vyjadriť p:X=A+t\vec{u}, číslo t nazývame parameter.
Ako súvisí hodnota parametra t s polohou bodu na priamke
- Priamka p je určená bodom A a vektorom \vec{u}=\overrightarrow{AB}, teda p:X=A+t\vec{u}
- Pre hodnotu t=0 dostaneme: X=A+t\vec{u}=A+0\cdot \vec{u} … bod A
- Pre hodnotu t=1 dostaneme: X=A+t\vec{u}=A+1\cdot \vec {u} … bod B
- Pre hodnotu t=2 dostaneme: X=A+t\vec{u}=A+2\cdot \vec {u} … bod C
- Pre hodnotu t=\frac{1}{2} dostaneme: X=A+t\vec{u}=A+\frac{1}{2}\cdot \vec{u} … bod D (stred úsečky AB)
- Pre hodnotu t=-1 dostaneme: X=A+t\vec{u}=A-1\cdot \vec{u} … bod E
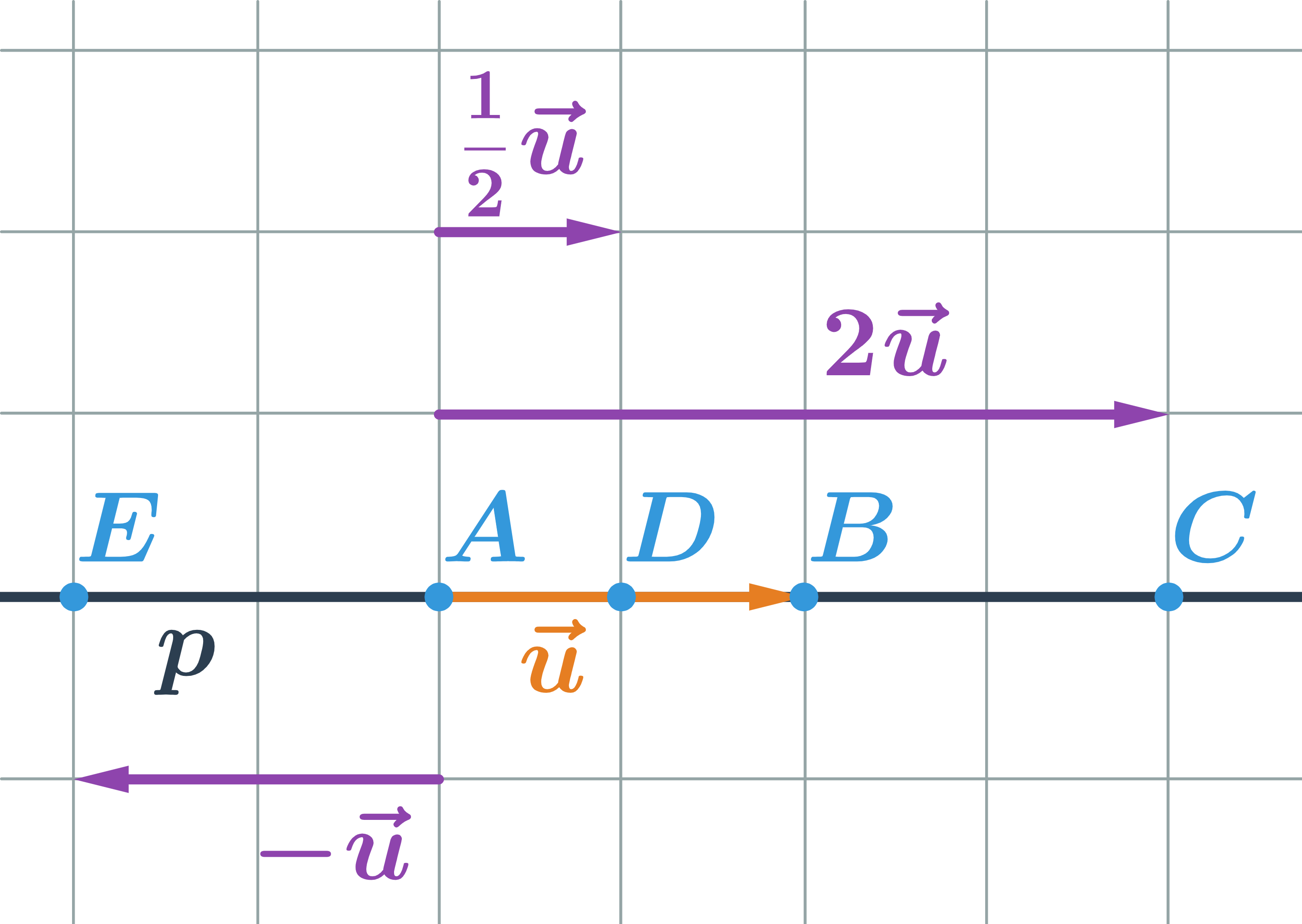
- Každá hodnota parametra určuje jeden bod na priamke, na určenie celej priamky teda potrebujeme všetky reálne čísla, preto píšeme t\in\mathbb{R}.
- Body, ktoré ležia na úsečke AB (teda body ležiace medzi bodmi A a B), vyjadríme parametricky, ak do rovnice X=A+t\vec{u} dosadíme hodnoty parametra t spĺňajúce 0\leq t\leq1.
Všeobecná rovnica priamky
Každý vektor kolmý k priamke p sa nazýva normálový vektor priamky p. Všeobecná rovnica priamky je rovnica v tvare: ax+by+c=0, kde konštanty a a b sú súradnice normálového vektora a c reálne číslo.
Súradnice smerového a normálového vektora priamky p
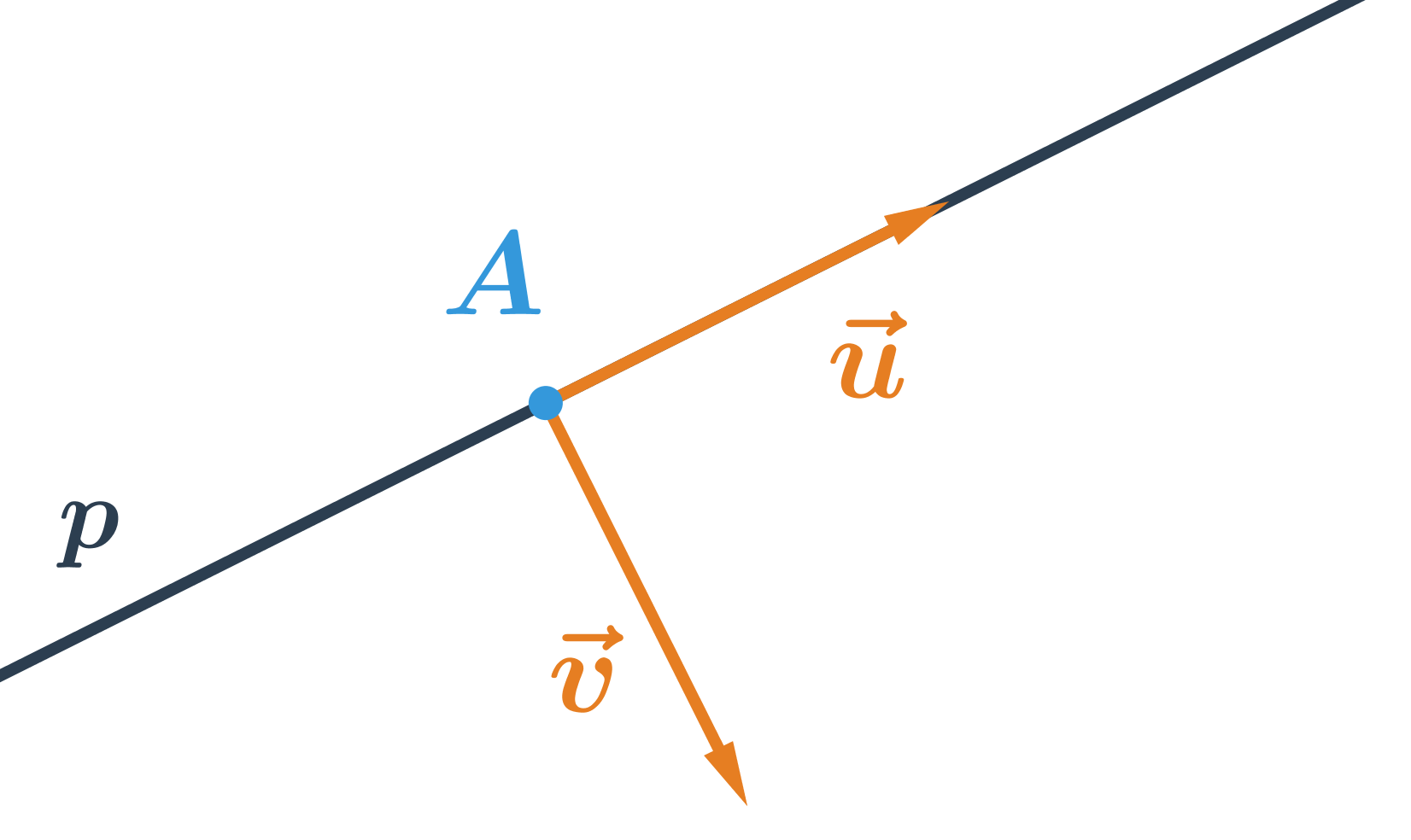
- Pre priamku danú všeobecnou rovnicou ax+by+c=0:
- \vec{v} je normálový vektor priamky p, jeho súradnice sú: \vec{v}=(a;b)
- \vec{u} je smerový vektor priamky p, pretože je to vektor kolmý na vektor \vec{v}=(a;b), jeho súradnice sú: \vec{u}=(-b;a)
- Pre priamku danú parametricky: \begin{array}{rrl}x&=&a_1+t\cdot u_1\\y&=&a_2+t\cdot u_2\\&&t\in\mathbb{R}\end{array}
- \vec{u} je smerový vektor priamky p, jeho súradnice sú: \vec{u}=(u_1;u_2)
- \vec{v} je normálový vektor priamky p, pretože je to vektor kolmý na vektor \vec{u}=(u_1;u_2), jeho súradnice sú: \vec{v}=(-u_2;u_1)
Všeobecná rovnica priamky rovnobežnej s osou x
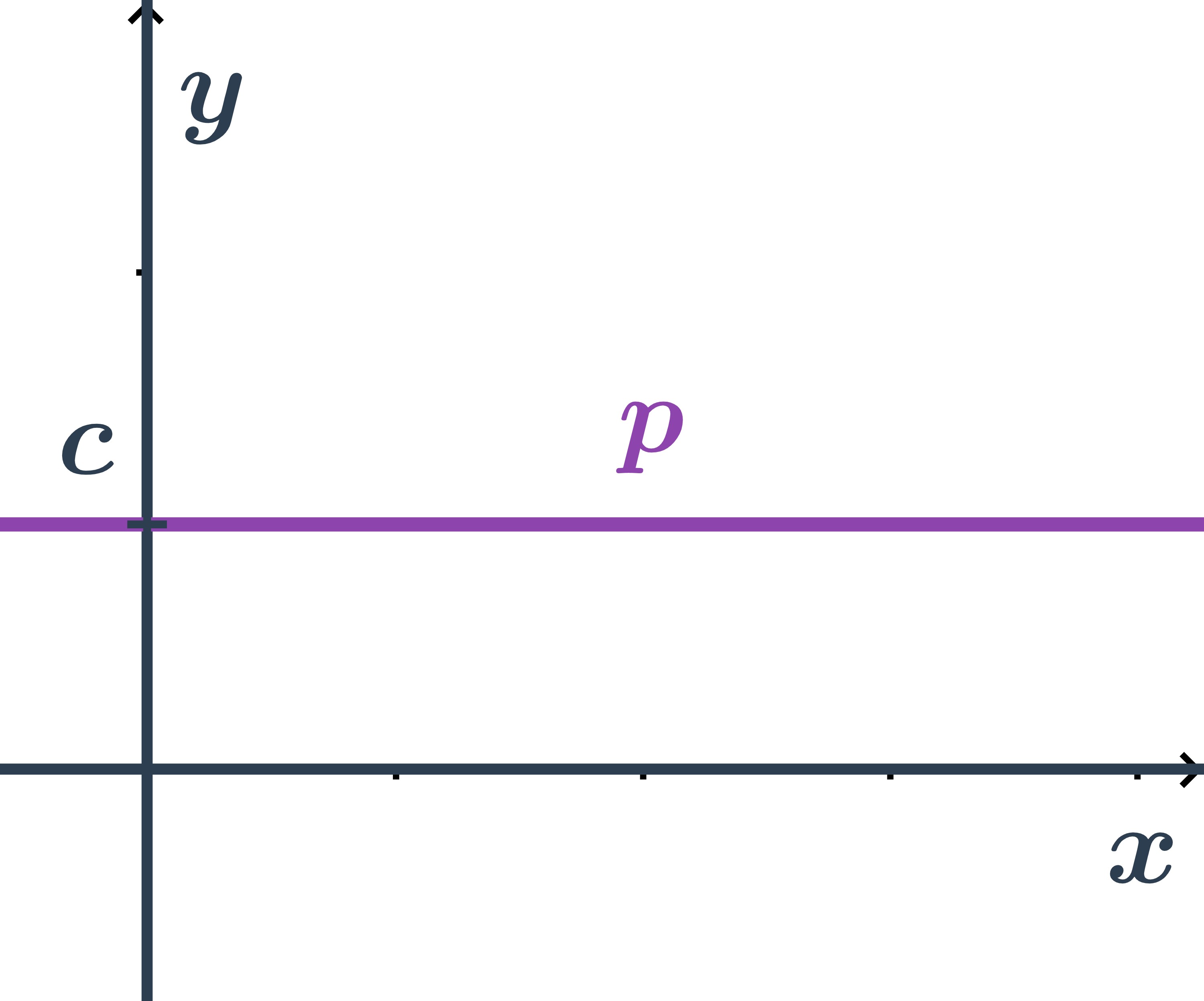
- Pre všetky body ležiace na priamke je druhá súradnica rovnaká a to: y=c
- Teda priamka má všeobecnú rovnicu: y-c=0
Všeobecná rovnica priamky rovnobežnej s osou y
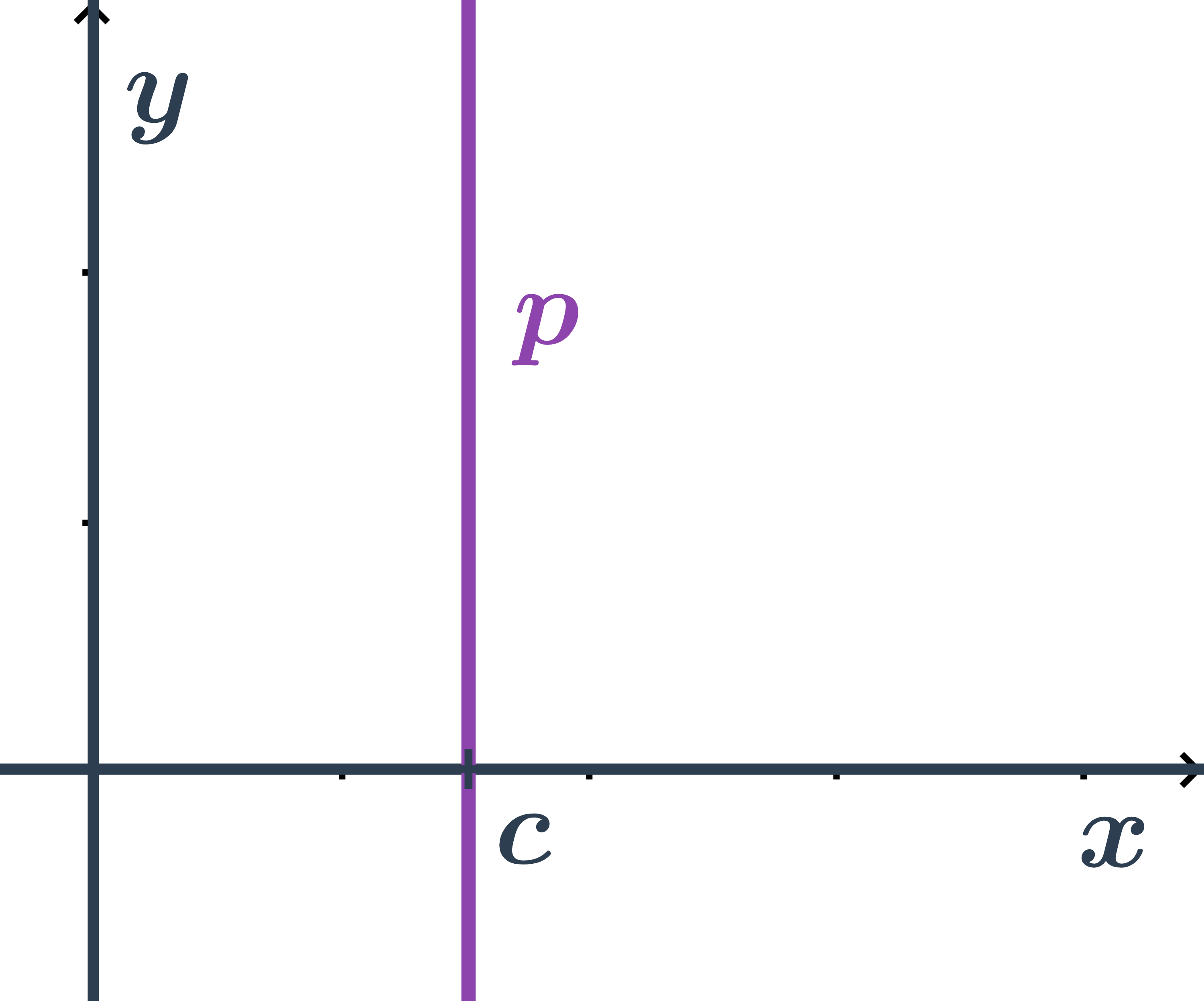
- Pre všetky body ležiace na priamke je prvá súradnica rovnaká a to: x=c
- Teda priamka má všeobecnú rovnicu: x-c=0
Bod a priamka
Bod M=[m_1;m_2] leží na priamke, ak jeho súradnice vyhovujú rovnici priamky. Ak je priamka daná všeobecnou rovnicou ax+by+c=0, pre súradnice bodu, ktorý leží na priamke platí: a\cdot m_1+b\cdot m_2+c=0. Ak je priamka daná parametricky, po dosiahnutí súradníc bodu vychádza z oboch rovníc rovnaká hodnota parametra t. (Viac o vzájomnej polohe bodu a priamky.)
Všeobecná rovnica priamky, ktorá prechádza počiatkom
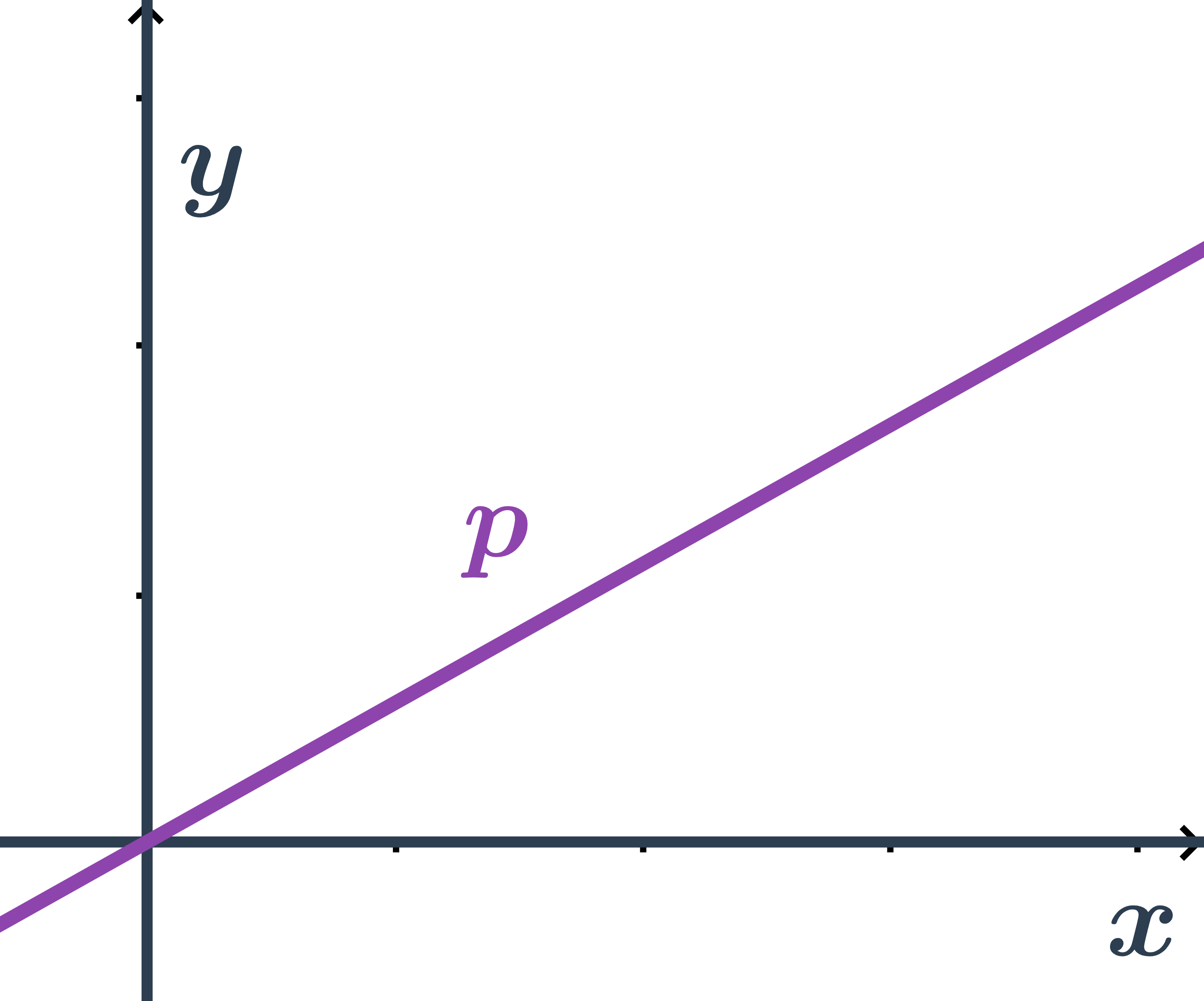
- Priamka prechádza bodom O=[0;0], teda súradnice počiatku spĺňajú jej všeobecnú rovnicu ax+by+c=0.
- Dosadíme súradnice bodu O a skúsime zistiť nejaké informácie o konštantách a,b,c.
- a\cdot0+b\cdot0+c=0\Leftrightarrow c=0
- Preto má priamka, ktorá prechádza počiatkom, všeobecnú rovnicu ax+by=0.
Dve priamky
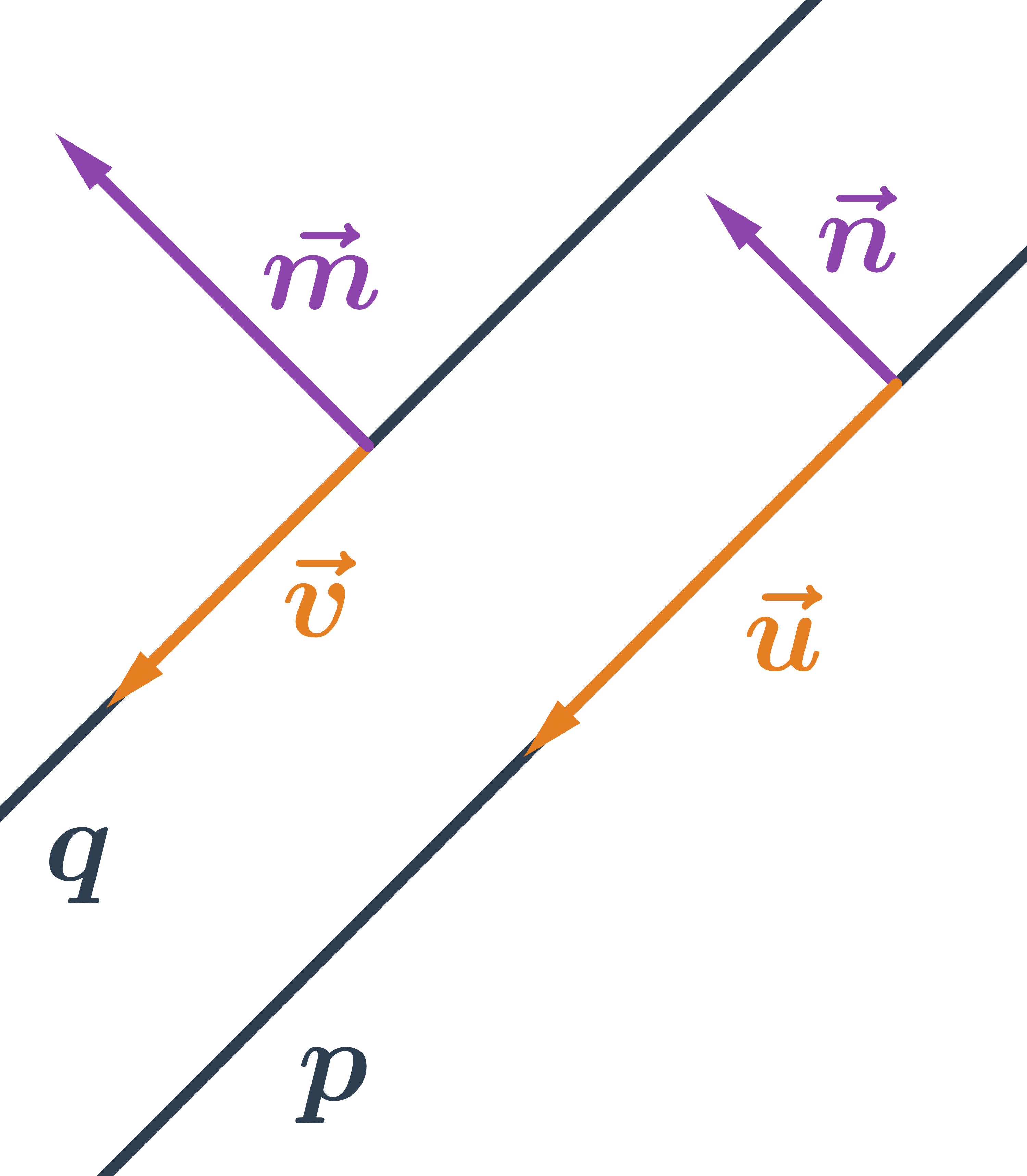
Priamky rovnobežné majú rovnaký smer, teda ich smerové vektory sú kolineárne. Normálové vektory dvoch rovnobežných priamok sú tiež kolineárne. V špeciálnom prípade môžu byť priamky totožné.
Priamky rôznobežné majú jeden spoločný bod, tento bod musí spĺňať rovnice oboch priamok. Ich smerové vektory nie sú kolineárne, normálové vektory tiež nie sú kolineárne.
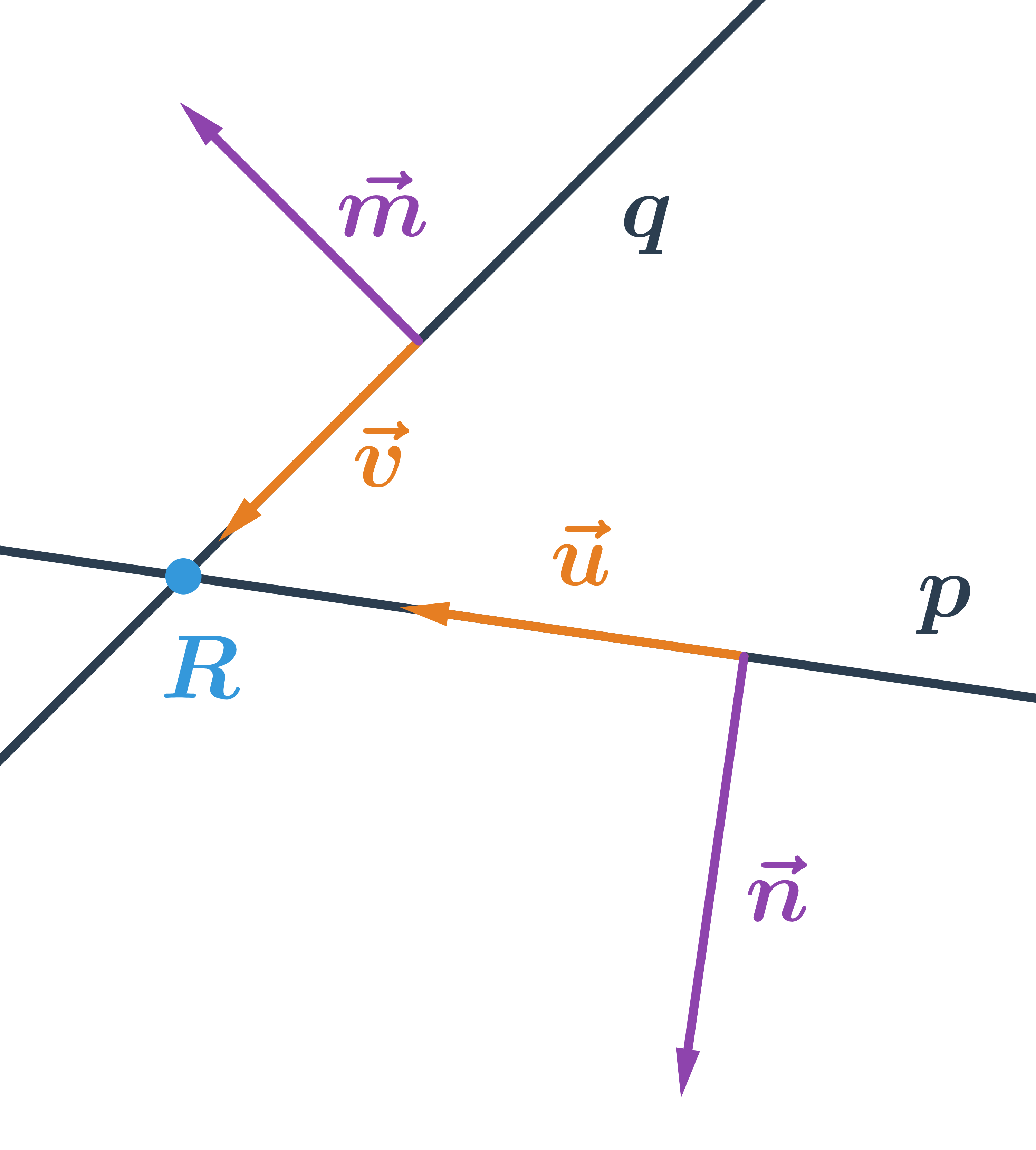
Viac o vzájomnej polohe dvoch priamok.
Priamka v priestore
Priamku v priestore nie je možné vyjadriť všeobecnou rovnicou. Parametrickú rovnicu priamky v priestore určíme podobne ako v rovine na základe znalosti súradníc smerového vektora a jedného bodu na priamke.
Priamky: pojmy (stredné)
Vyriešené:
