Slovenčina
Angličtina
Informatika
Vieme to
Nemčina
Biológia
Zemepis
Chémia
Fyzika
Aritmetika
Zlomky, percentá, desatinné čísla
Geometria
Elementárna algebra
Funkcie
Jednotky, miery
Diskrétna matematika
Finančná gramotnosť
Rozhodovačka
Pexeso
Krok za krokom
Počítanie
Grafár
Porozumenie
Označovanie
Presúvanie
Mriežkovaná
Rozdeľovačka
Pokazená kalkulačka
Roboti
Strieľačka
Príšerky
Preteky
Územia
Tímovka
Môj účet
Odhlásiť sa
Rozhodovačka
Stred úsečky v rovine
Precvičujte neobmedzeneVáš denný počet odpovedí je obmedzený. Pre navýšenie limitu alebo prístup do svojho účtu s licenciou sa prihláste.
Prihlásiť sa
GM4
QR kód
Kód / krátka adresa
Skopírujte kliknutím.
Nastavenie cvičení
Pozor, nastavenie je platné iba pre toto cvičenie a predmet.
Stred úsečky v rovine
Stred úsečky delí úsečku na dve rovnaké časti. Ak ležia krajné body úsečky AB na číselnej osi a ich polohám zodpovedajú hodnoty a a b, potom jej stredu S zodpovedá číslo s=\frac{a+b}{2}. Stred úsečky je „priemerom“ jej krajných bodov.
Pre úsečku v rovine bude situácia nasledujúca. 
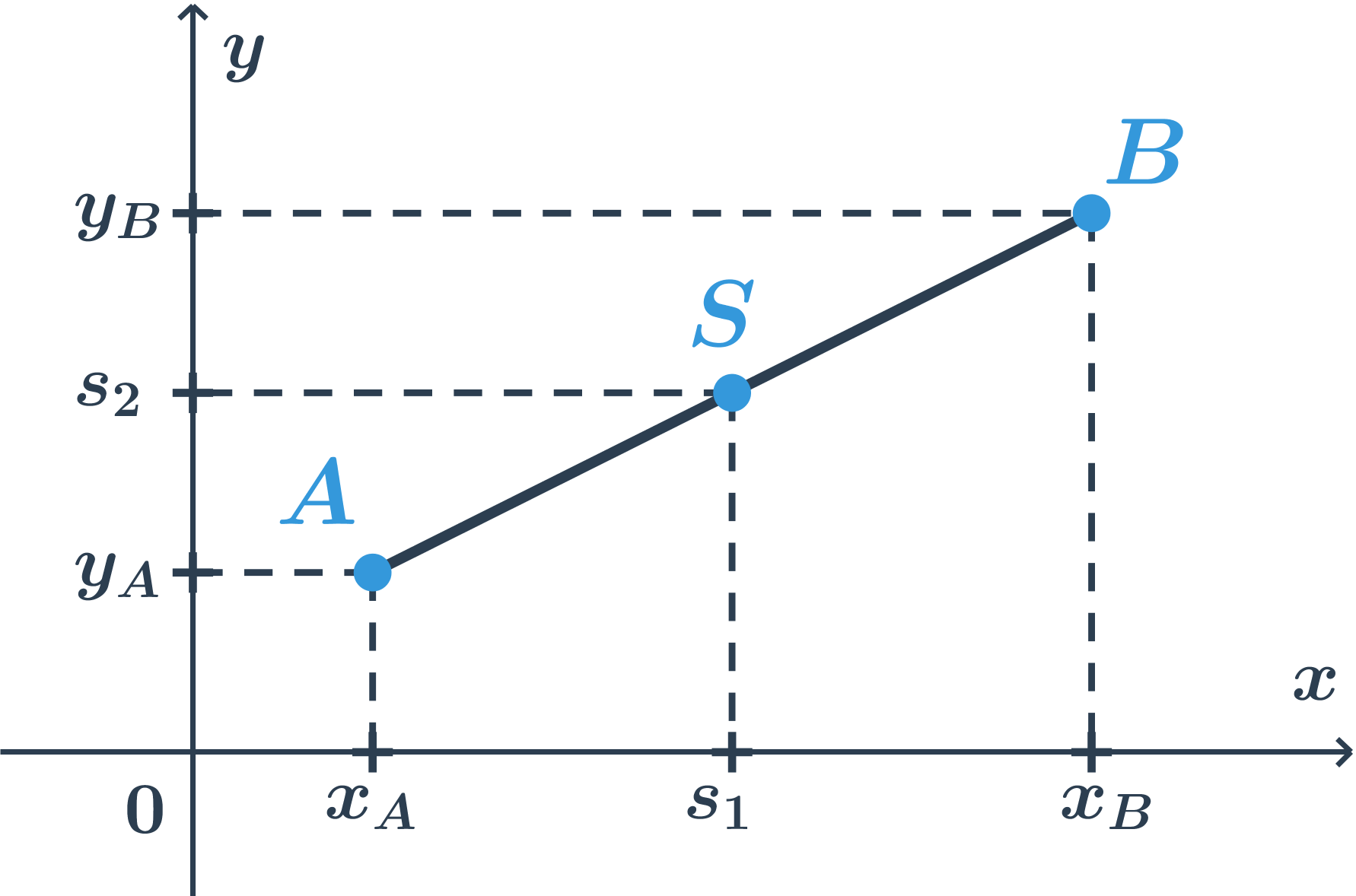Situácia na oboch súradných osách je rovnaká ako predtým. Vypočítame obe súradnice stredu ako priemery zodpovedajúcich súradníc krajných bodov.
Pre stred S[s_1;s_2] úsečky AB, kde A[x_A; y_A], B[x_B; y_B] platí:
s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
Príklad: určenie stredu úsečky
Nájdite stred úsečky AB: A[6;-1], B[2;3]
- Pre súradnice stredu S[s_1;s_2] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
- Dosadíme súradnice bodov A[6;-1], B[2;3]: s_1 = \frac{6+2}{2}=4, s_2 = \frac{-1+3}{2}=1
- Stred úsečky AB je bod S[4;1]
Príklad: určenie druhého krajného bodu úsečky
Určite súradnice druhého krajného bodu úsečky AB, ak je daný bod A[-3;0] a jej stred S[1;3].
- Pre súradnice stredu S[s_1;s_2] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
- Dosadíme súradnice bodov A[-3;0], S[1;3]: 1 = \frac{-3+x_B}{2}, 3 = \frac{0+y_B}{2}
- Dopočítame neznáme x_B, y_B: 2=-3+x_B\Rightarrow x_B=5\\ 6=0+y_B\Rightarrow y_B=6
- Bod B má súradnice [5;6].
Stred úsečky v rovine (stredné)
Vyriešené:
