Výpis prehľadov
Grafy funkcií
Podkapitoly
Grafy funkcií
Graf funkcie f zadanej predpisom y=f(x) pre všetky x z množiny D(f) je množina bodov v rovine, ktorých karteziánske súradnice x, y spĺňajú nasledujúce podmienky:
- súradnica x je v definičnom obore funkcie f (teda x \in D(f))
- závislosť súradnice y od x je popísaná funkčným predpisom y=f(x) (pre každé x z D(f) je v grafe presne jeden bod, jeho súradnice sú x a f(x))
Príklad: graf, definičný obor, obor hodnôt funkcie
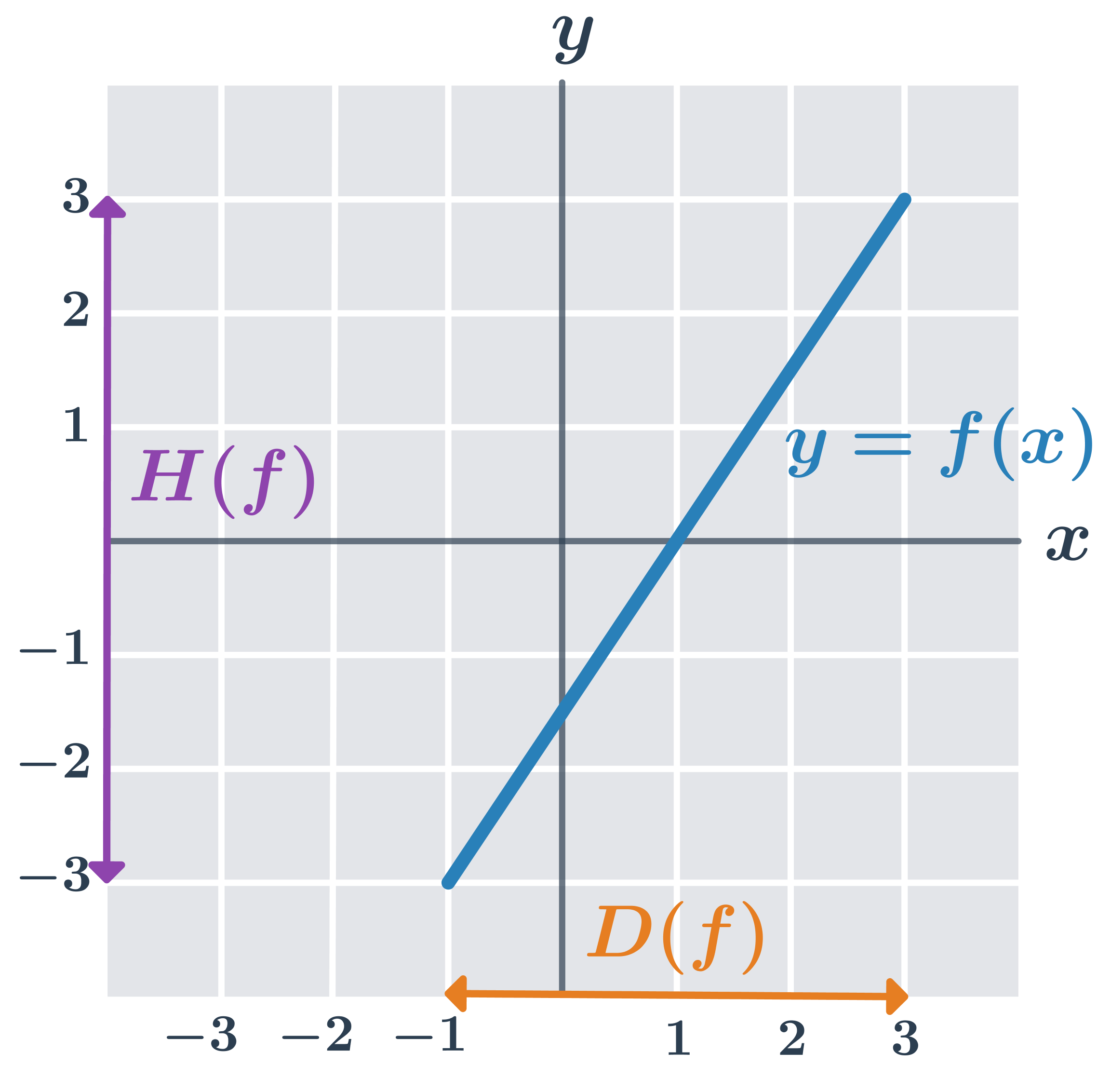
Na obrázku je graf funkcie y=2x-1 pre x\in \langle -1;3\rangle. Definičný obor je vyznačený na osi x, obor hodnôt na osi y.
Grafy lineárnych funkcií
Lineárnu funkciu môžeme vždy zapísať v tvare f(x) = a\cdot x + b, kde a a b sú konštanty. Parameter a je smernica (tiež nazývaná sklon), parameter b je absolútny člen. Grafom lineárnej funkcie je priamka, pričom platí:
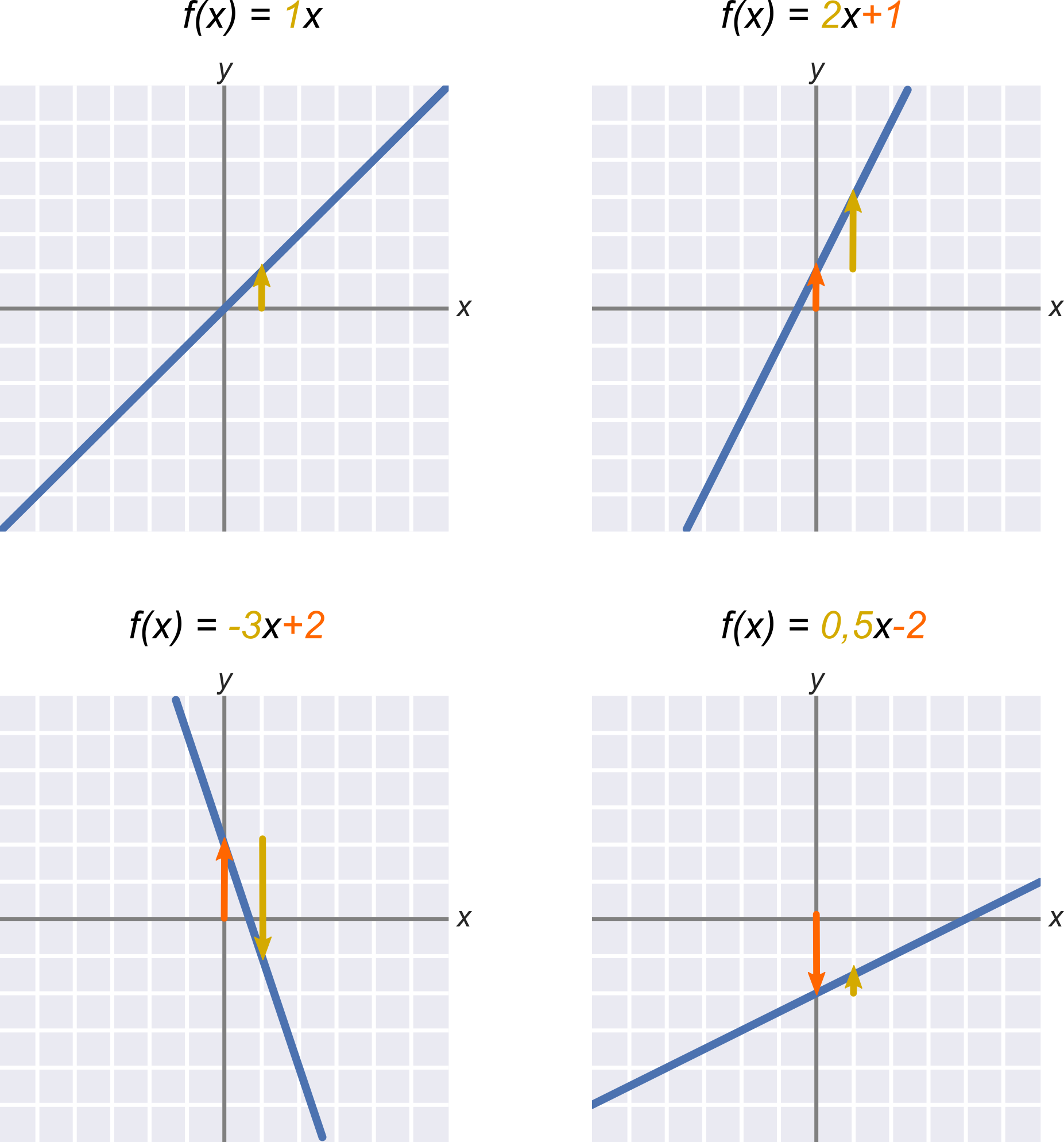
- Absolútny člen b udáva „zvislý posun“. Je to priesečník priamky s osou y. V uvedených príkladoch je vyznačený oranžovou farbou.
- Smernica a udáva sklon priamky, čo môžeme vyjadriť ako „o koľko jednotiek na osi y sa priamka posunie za jednu jednotku na osi x“. V uvedených príkladoch je smernica vyznačená žltou farbou.
Dôležité sú znamienka (naznačené v obrázkoch šípkami). Kladný absolútny člen znamená posun hore, záporný absolútny člen znamená posun dole. Kladná smernica znamená stúpajúcu priamku, záporná smernica znamená klesajúcu priamku.
Grafy kvadratických funkcií
Kvadratickú funkciu je možné vyjadriť v tvare f(x) = ax^2 + bx + c, kde a\neq 0. Grafom kvadratickej funkcie je parabola. Tento graf zobrazuje funkciu 0{,}5 x^2 + x - 4:
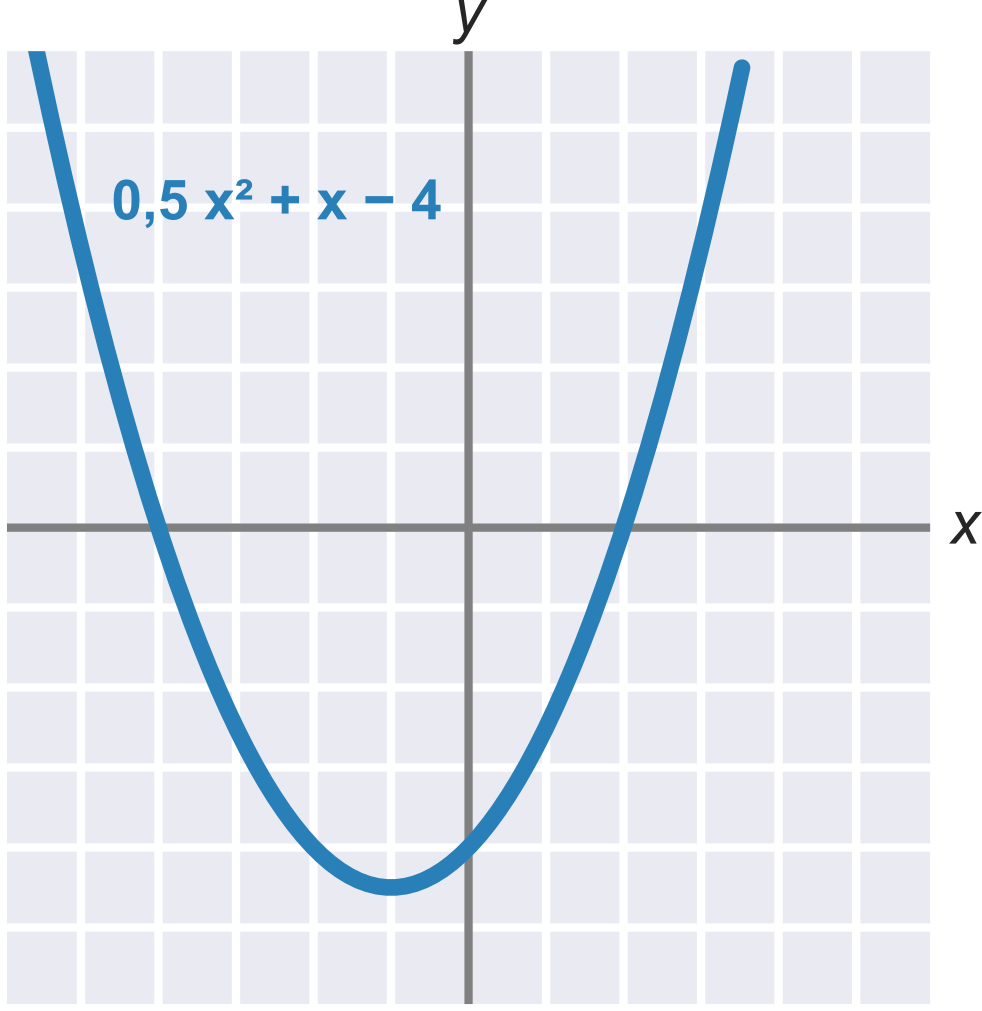
Priesečníky s osou x sú riešenia kvadratickej rovnice ax^2 + bx + c = 0. Pre vyššie uvedený príklad 0{,}5 x^2 + x - 4 sú týmito riešeniami x_1 = -4 a x_2 = 2.
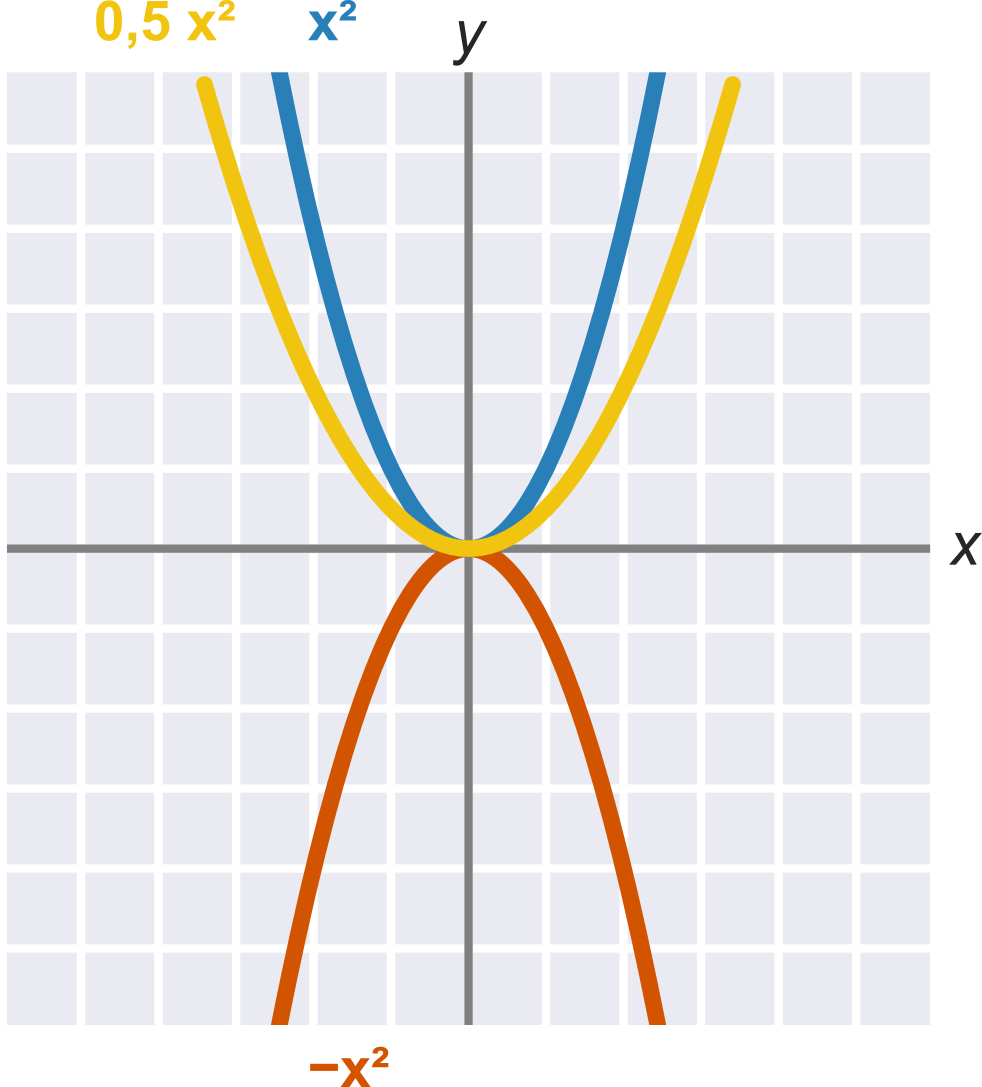
Kvadratický koeficient a ovplyvňuje základnú podobu paraboly:
- Ak je a > 0, „smeruje parabola hore“ (presnejšie: je to zdola ohraničená, konvexná funkcia).
- Ak je a \lt 0, „smeruje parabola dole“ (presnejšie: je to zhora ohraničená, konkávna funkcia).
- Veľkosť kvadratického koeficientu a ovplyvňuje, ako je parabola „široká“.
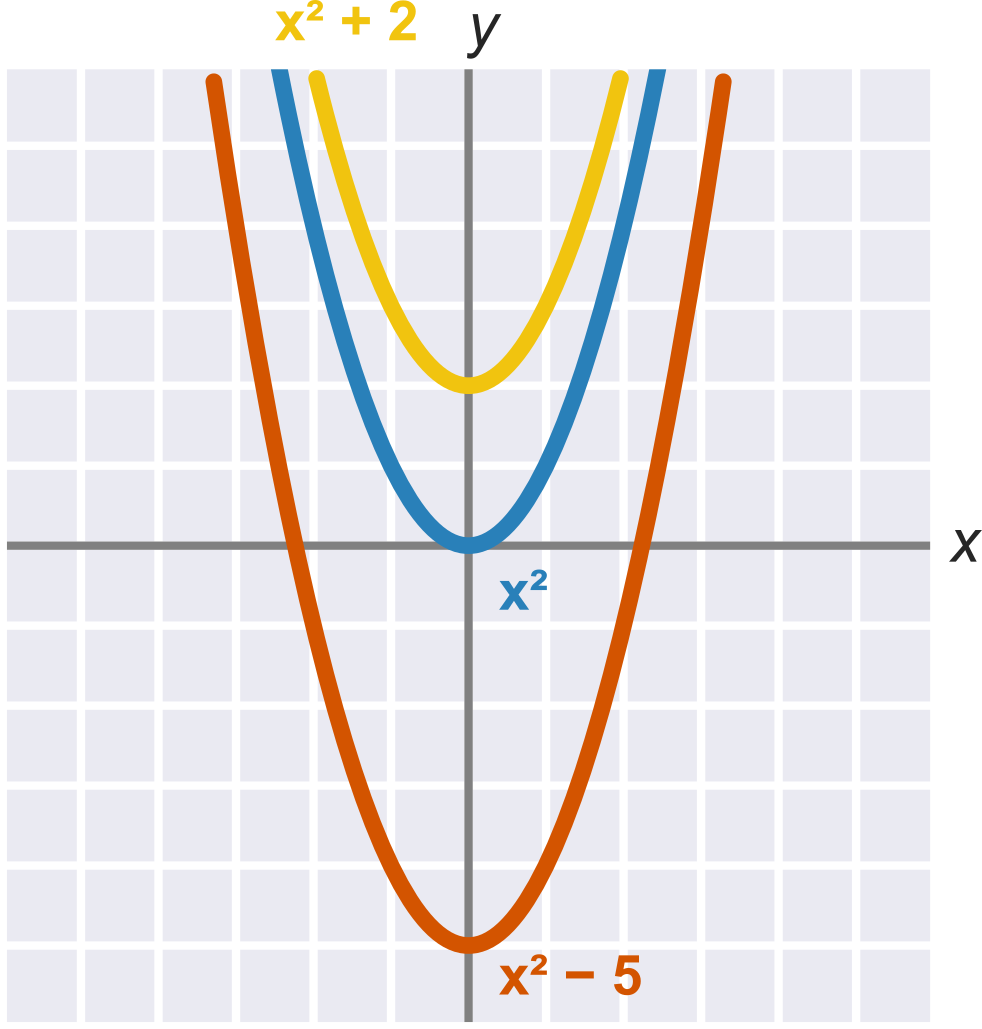
Konštantný člen c ovplyvňuje posun paraboly – udáva priesečník s osou y.
Grafy funkcií s absolútnou hodnotou
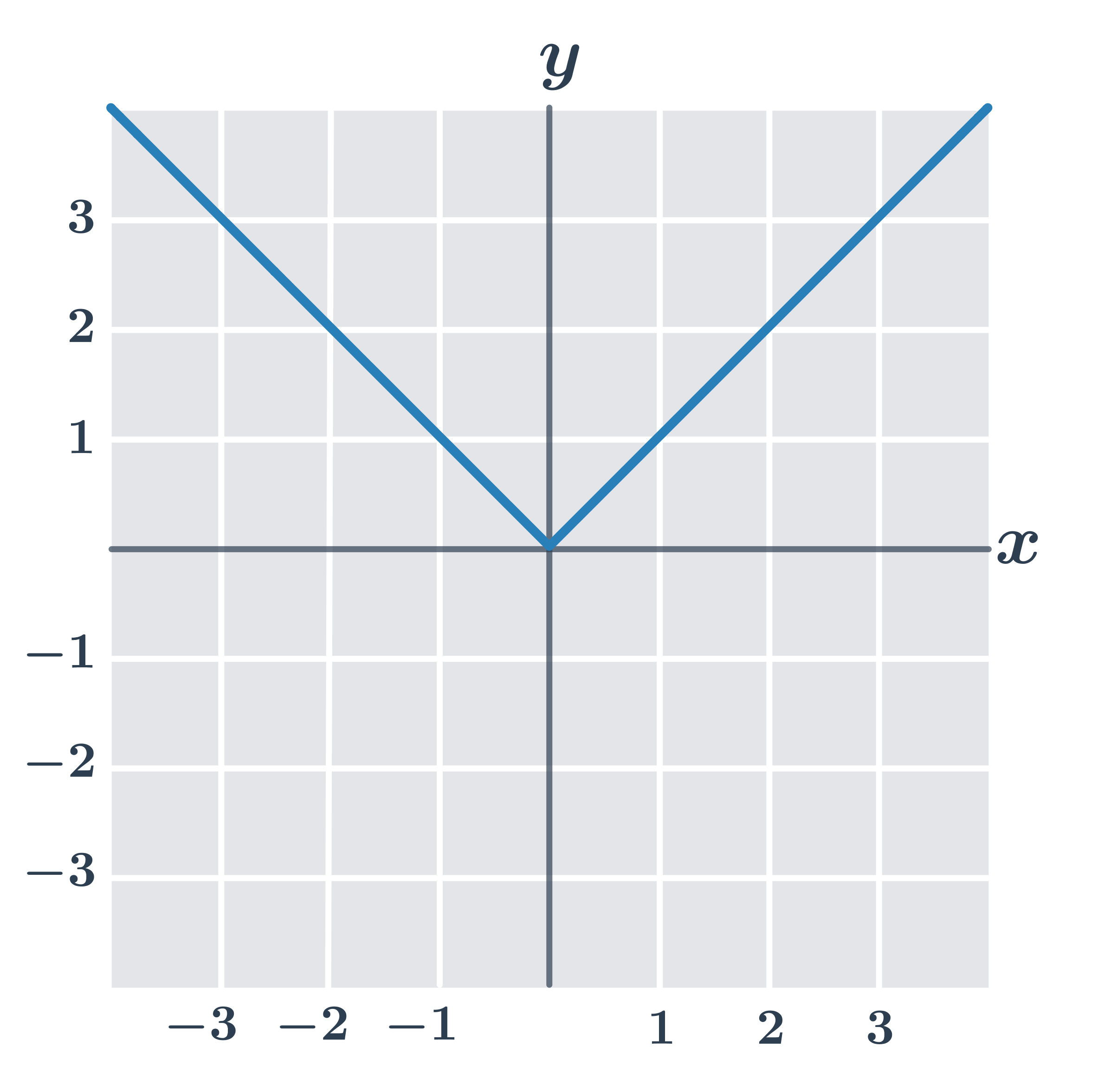
Na obrázku je graf funkcie y=|x|. Tento graf tvoria dve polpriamky s počiatkom v bode [0;0], pretože pre absolútnu hodnotu platí:
- absolútna hodnota kladného čísla je rovná tomuto číslu: |x|=x
- absolútna hodnota záporného čísla je rovná opačnému číslu: |x|=-x
- absolútna hodnota čísla nula je rovná nule: |0|=0
| x \gt 0 | Grafom funkcie y=|x| je polpriamka s počiatkom v bode [0;0] daná rovnicou y=x. |
| x \lt 0 | Grafom funkcie y=|x| je polpriamka s počiatkom v bode [0;0] s rovnicou y=-x. |
| x = 0 | Bod [0;0] je počiatok polpriamok, ktoré vytvoria graf funkcie y=|x|. |
Ak chceme nakresliť graf funkcie y=|f(x)| postupujeme tak, že nakreslíme graf y=f(x) a potom záporné funkčné hodnoty nahradíme opačnými. V oblasti, kde sú funkčné hodnoty záporné, sa teda graf preklopí okolo osi x.
Príklad 1: graf funkcie y=|x-1|
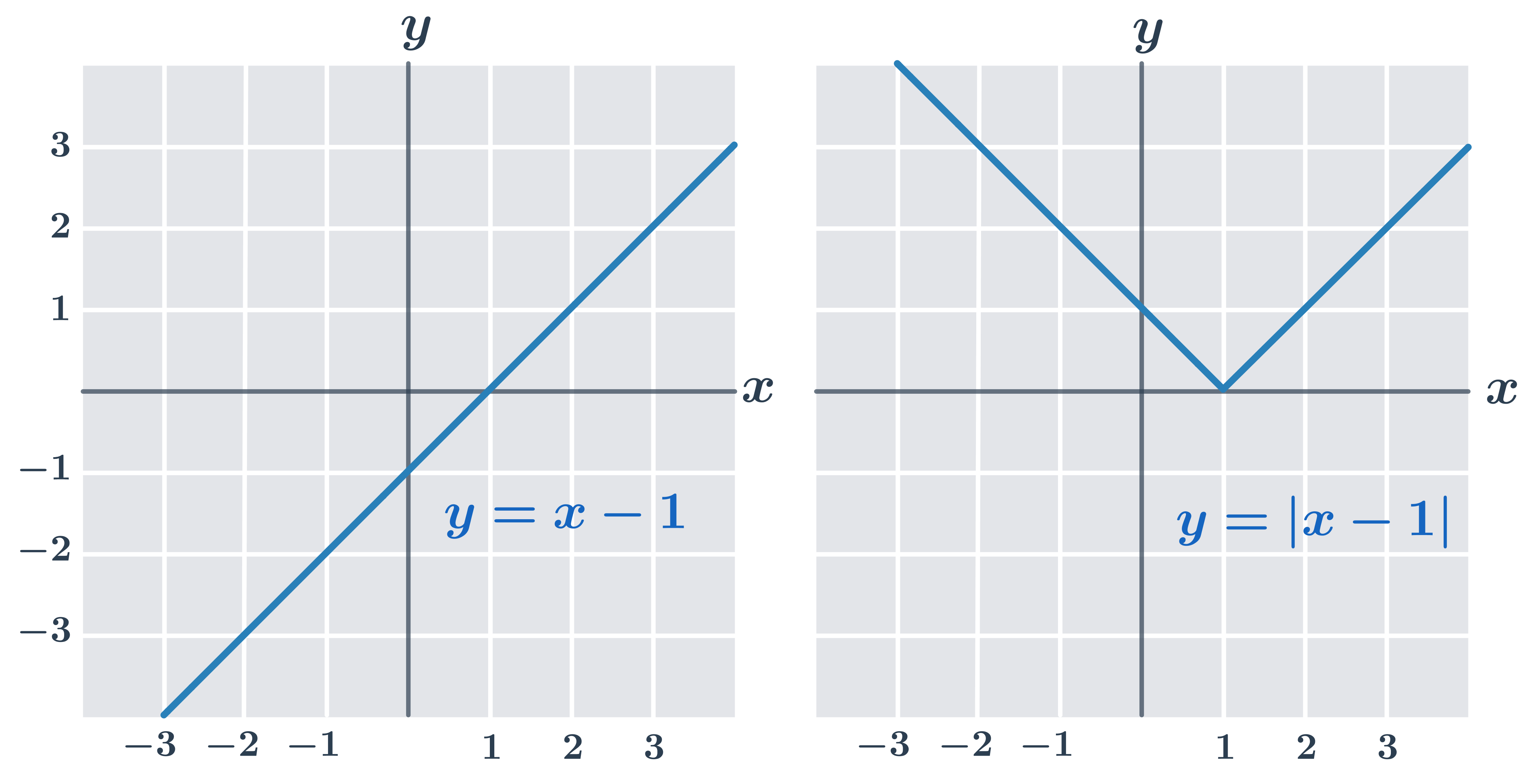
| Pre čísla x \lt 1 má funkcia y=x-1 záporné funkčné hodnoty. |
| Funkcia y=|x-1| má v intervale (-\infty;1) opačné hodnoty než funkcia y=x-1 (graf y=|x-1| je voči grafu y=x-1 v tomto intervale preklopený podľa osi x). |
| V intervale (1;\infty) sú grafy funkcií y=x-1 a y=|x-1| rovnaké. |
Príklad 2: graf funkcie y=|x^2-4|
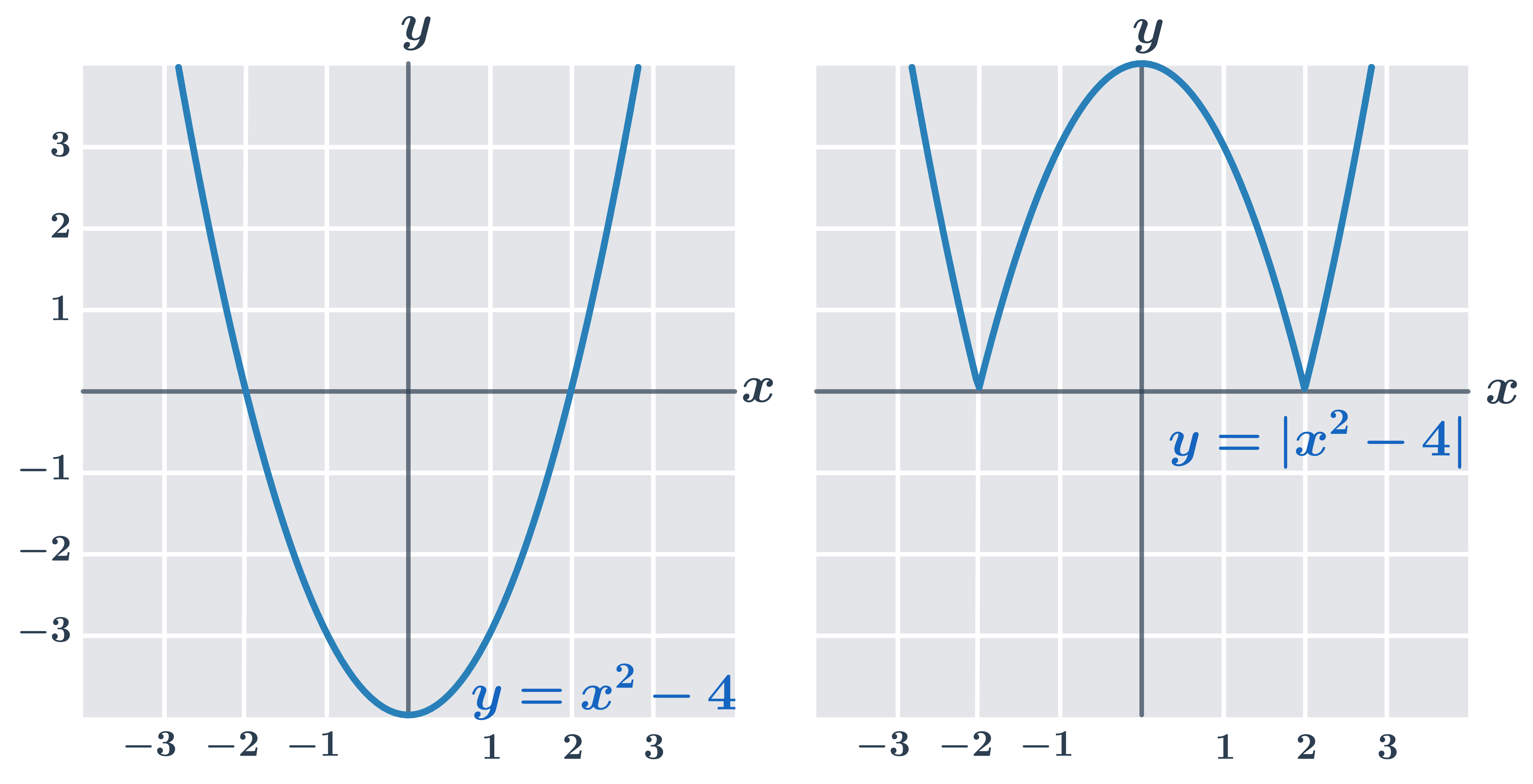
| V intervale (-2;2) má funkcia y=x^2-4 záporné funkčné hodnoty. |
| Funkcia y=|x^2-4| má v intervale (-2;2) opačné hodnoty než funkcia y=x^2-4 (graf je preklopený podľa osi x). |
| V intervaloch (-\infty;-2) a (2;\infty) sú grafy funkcií y=x^2-4 a y=|x^2-4| rovnaké. |
Grafy lineárnych lomených funkcií
Grafom lineárnej lomenej funkcie je hyperbola, ktorá má asymptoty rovnobežné so súradnicovými osami x a y.
Asymptota rovnobežná s osou y prechádza bodom, ktorý nepatrí do definičného oboru a má teda rovnicu: x =-\frac{d}{c}.
Na nájdenie rovnice asymptoty rovnobežnej s osou x vydelíme čitateľa a menovateľa a funkčný predpis y =\frac{ax+b}{cx+d} upravíme na tvar y =\frac{a}{c}+\frac{n}{ax+b}. Asymptota rovnobežná s osou x má rovnicu: y =\frac{a}{c}.
Priesečník grafu s osou x je bod, pre ktorý ax+b=0. V tomto bode je hodnota funkcie nulová, teda čitateľ zlomku \frac{ax+b}{cx+d} je nulový.
Priesečník grafu s osou y je bod, ktorý dostaneme dosadením hodnoty x=0 do funkčného predpisu.
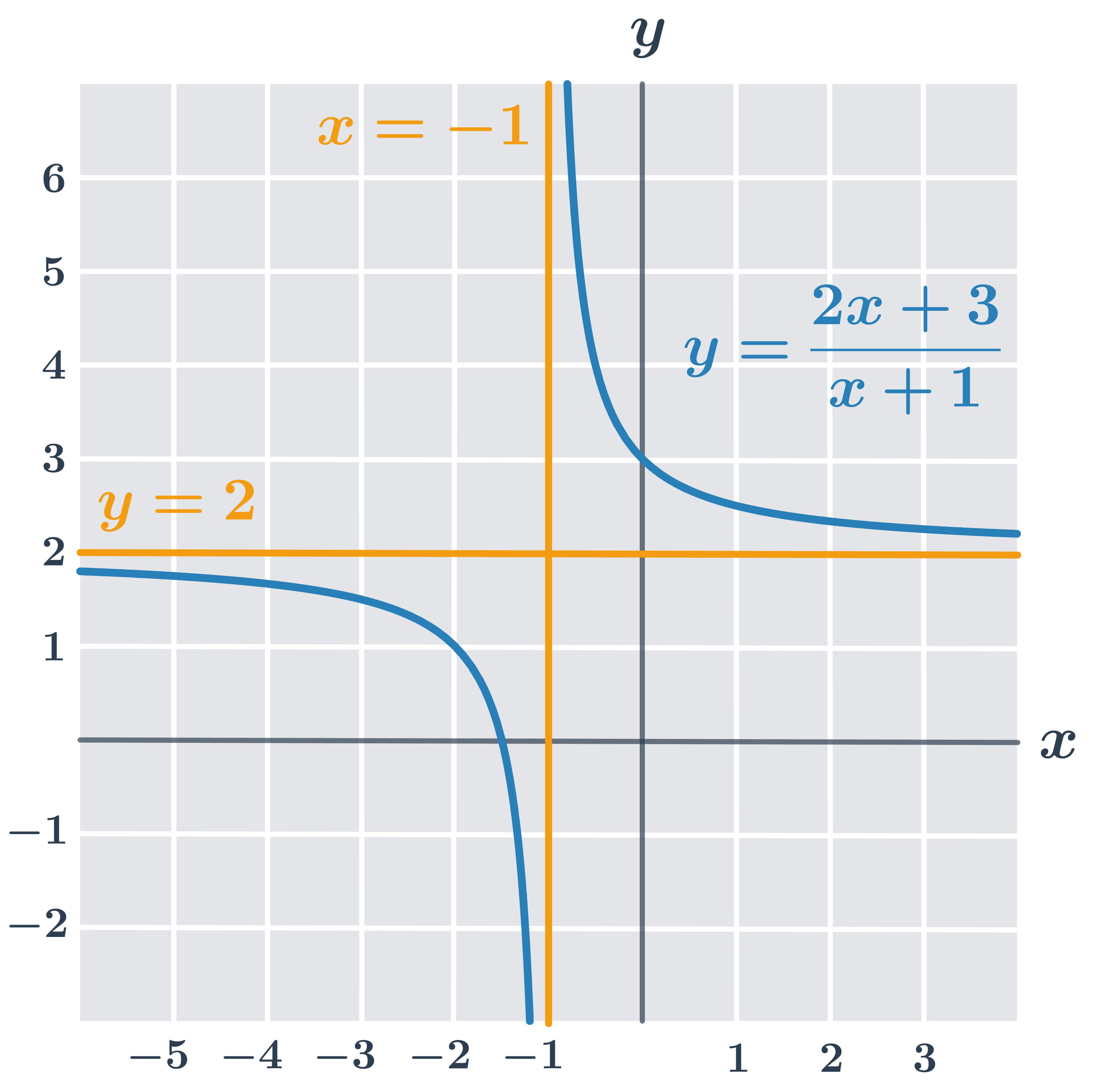
Príklad – funkcia y =\frac{2x+3}{x+1}
Rozoberme si graf funkcie z obrázka vyššie:
- definičný obor D(f)=\R - \{-1\}, pretože x+1\neq0
- asymptota rovnobežná s osou y má rovnicu x =-1 (pre x=-1 nie je funkcia definovaná, toto číslo neleží v jej definičnom obore)
- asymptota rovnobežná s osou x má rovnicu y =2, čo zistíme úpravou funkčného predpisu: y =\frac{2x+3}{x+1}=2+\frac{1}{x+1}
- priesečník grafu s osou x je bod [0;-\frac{3}{2}] (riešenie rovnice: 2x+3=0)
- priesečník grafu s osou y je bod [3;0], dosadením hodnoty x=0 do y =\frac{2x+3}{x+1}
Grafy mocninových funkcií
Grafy základných mocninových funkcií y= x^n
pre párne n – graf je súmerný podľa osi y, D(f)=\R, H(f)=\langle0, \infty)
pre nepárne n – graf je súmerný podľa počiatku, D(f)=\R, H(f)=\R
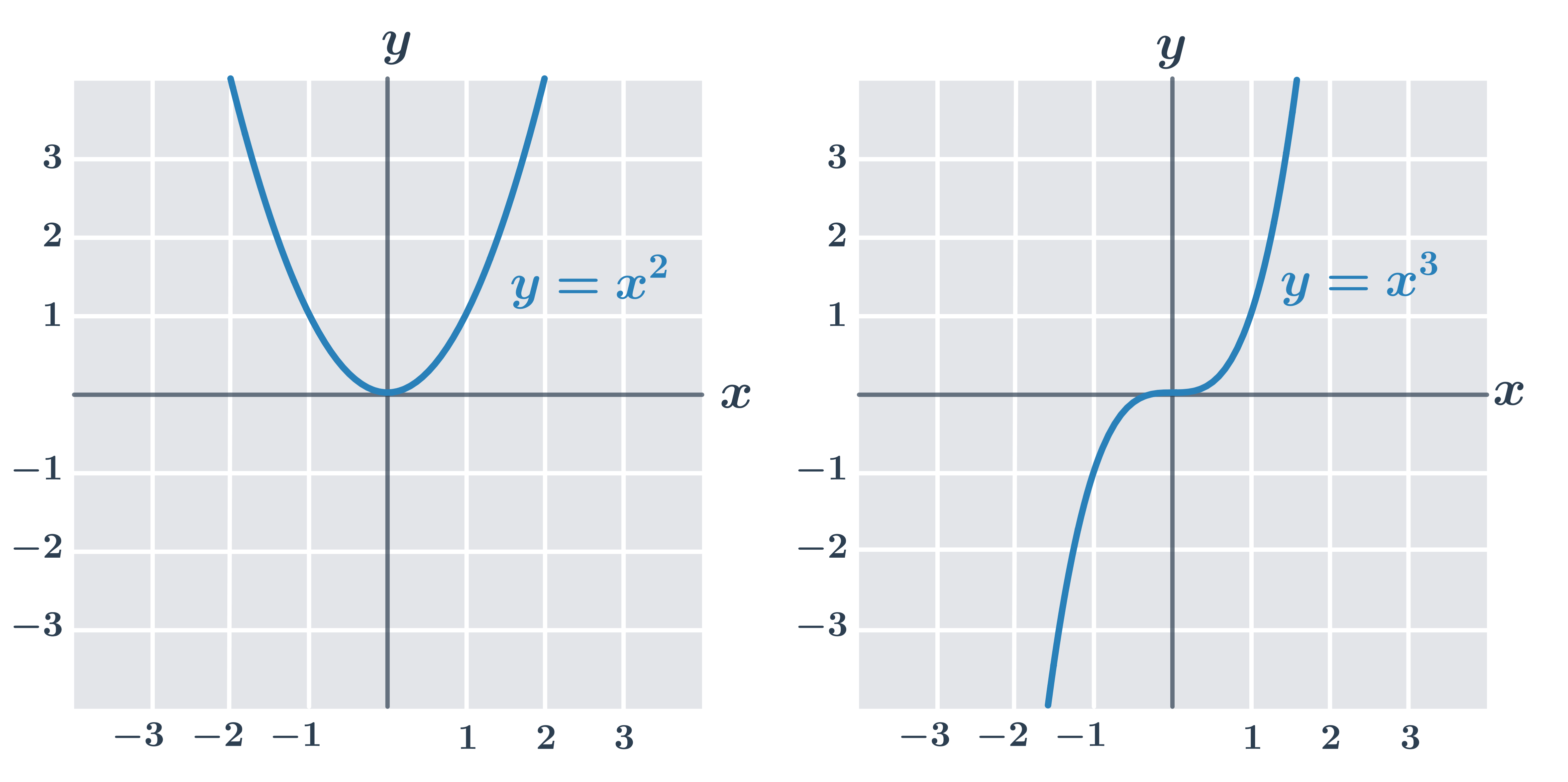
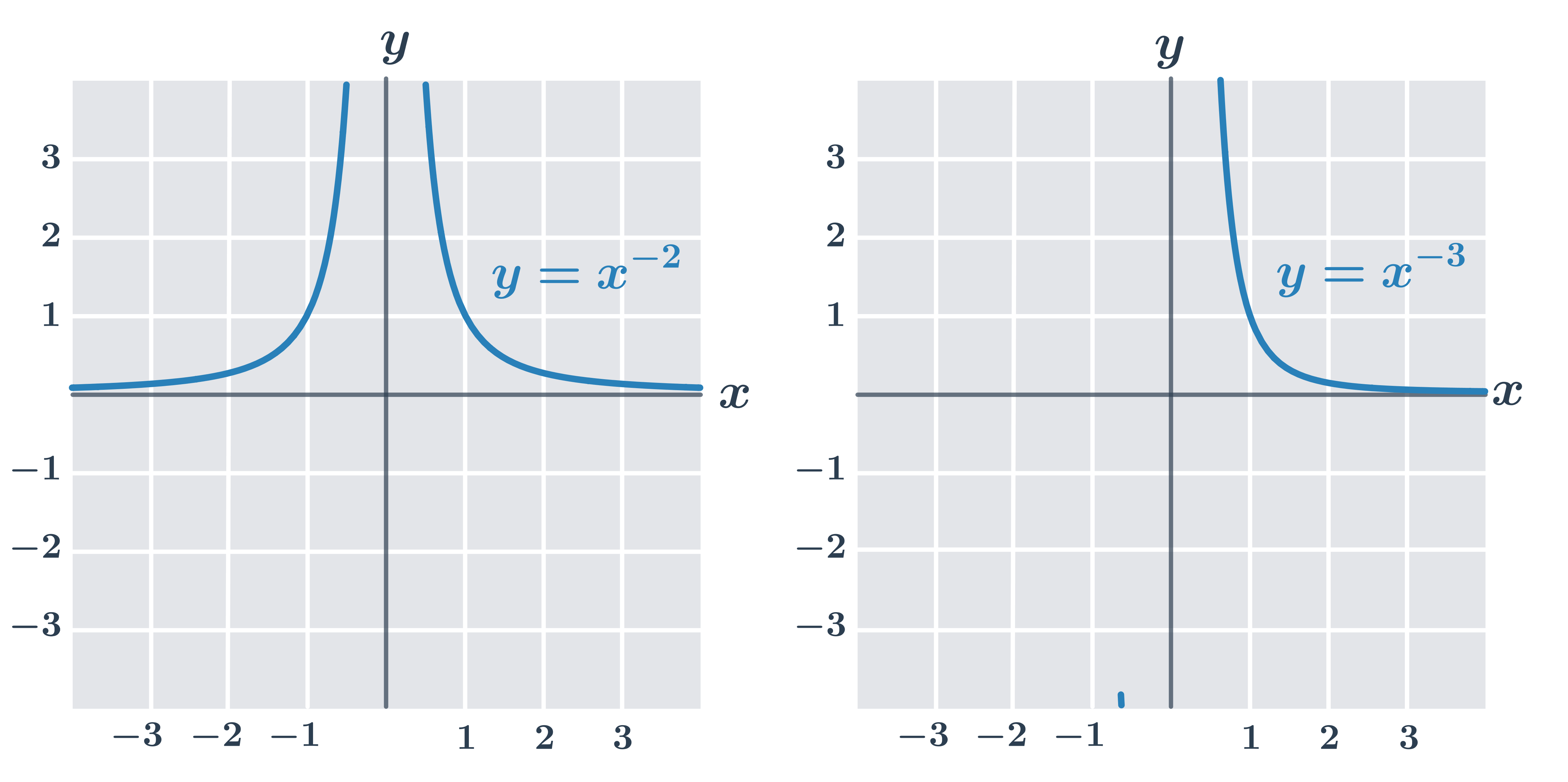
Grafy mocninových funkcií so záporným exponentom y= x^{-n}
pre párne n – graf súmerný podľa osi y, D(f)=\R- \{0\}, H(f)=\langle0, \infty)
pre nepárne n – graf súmerný podľa počiatku, D(f)=\R - \{0\}, H(f)=\R - \{0\}
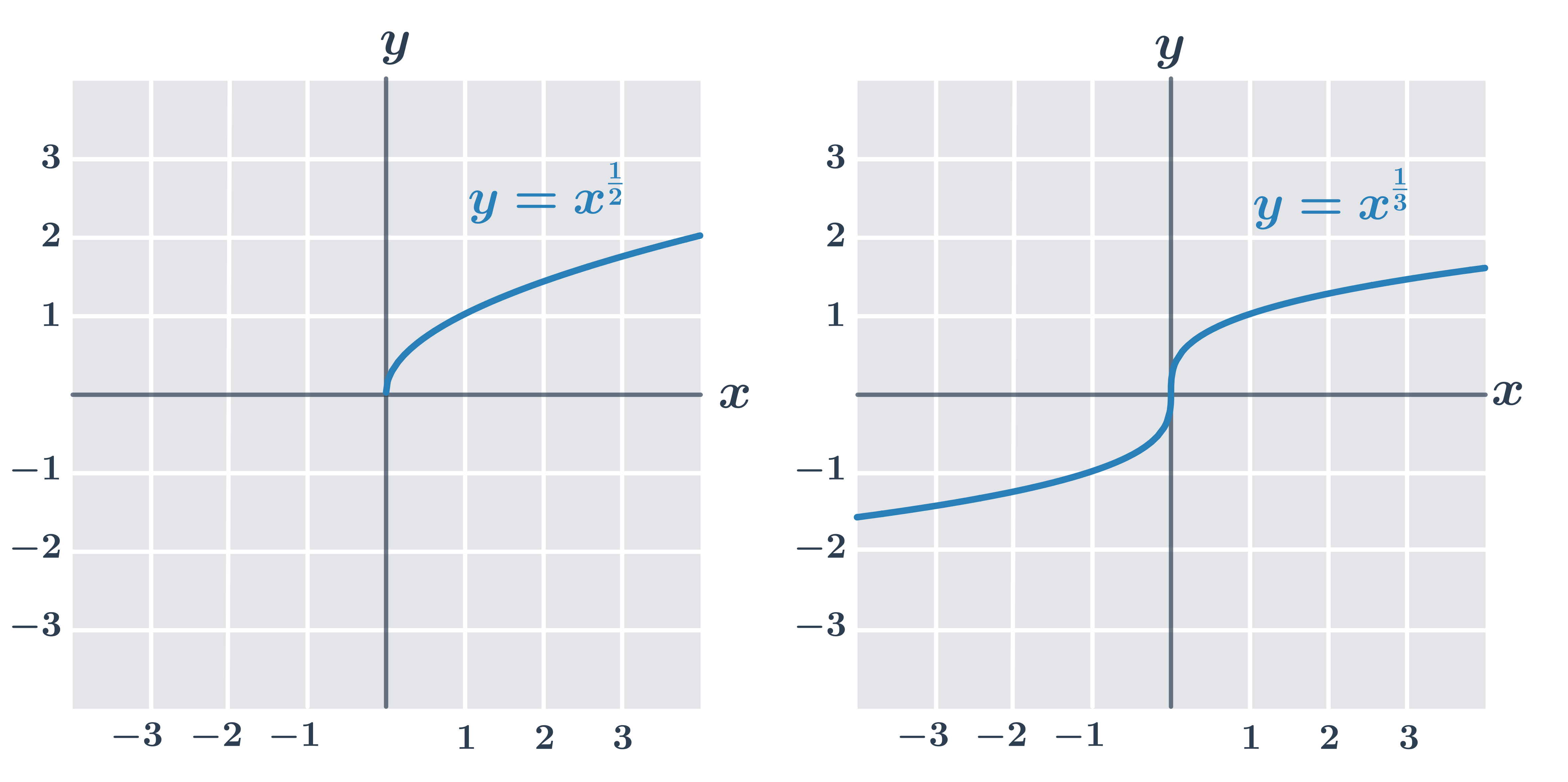
Grafy funkcií y= x^{\frac{1}{n}}:
pre párne n – funkcia y= x^{\frac{1}{n}} definovaná na kladných číslach, D(f)=\langle0, \infty), H(f)=\langle0, \infty)
pre nepárne n – funkcia y=x^n je jednoduchá, preto by sme mohli definovať n-tú odmocninu aj pre záporné čísla, ale často sa všetky n-té odmocniny pre párne aj nepárne n definujú pre jednoduchosť iba na intervale [0,\infty) (napr. ako príprava na prácu s mocninovými funkciami so všeobecnejšími racionálnymi exponentami) .
Poznámka: výpočty s mocninami a odmocninami
Pri výpočtoch s mocninami a odmocninami musíme byť obozretní; veľa pravidiel platí pre nezáporný základ (ak počítame s odmocninami), prípadne kladný základ (nulu môžeme odmocňovať, ale nesmieme deliť nulou). Príklady:
súčin odmocnín je odmocnina súčinu: pre nezáporné čísla ako základy odmocnín pravidlo platí, ak by sme chceli použiť pre záporný základ, nemusia nám v obore reálnych čísel vychádzať zmysluplné veci: \sqrt{-2} nie je definovaná, ale \sqrt{(-2)\cdot(-2)} je \sqrt{4} = 2
racionálne exponenty: malo by x^{\frac{2}{6}} byť to isté ako x^{\frac{1}{3}}? Exponent je „rovnaké racionálne číslo“, ale pre záporné x by vychádzali v prípade týchto dvoch predpisov iné funkčné hodnoty (6. odmocnina zo záporného x nie je definovaná, 6. odmocnina z druhej mocniny záporného čísla je kladná, a 3. odmocnina z x by bola pre záporné x záporná).
racionálne exponenty konkrétnejšie: čomu by sa malo rovnať (-8)^{\frac{2}{6}}? Máme (-8)^{\frac{1}{3}}=-2, ale zároveň \sqrt[6]{(-8)^2} = \sqrt[6]{64} = 2. Môžeme mať problém, keď budeme pravidlá, ktoré platia pre mocniny a odmocniny kladných a nezáporných čísel, skúšať používať aj pre záporné základy.
Vplyv úprav funkčného predpisu na graf mocninovej funkcie
Obrázok ukazuje niekoľko úprav funkcie y= x^3:
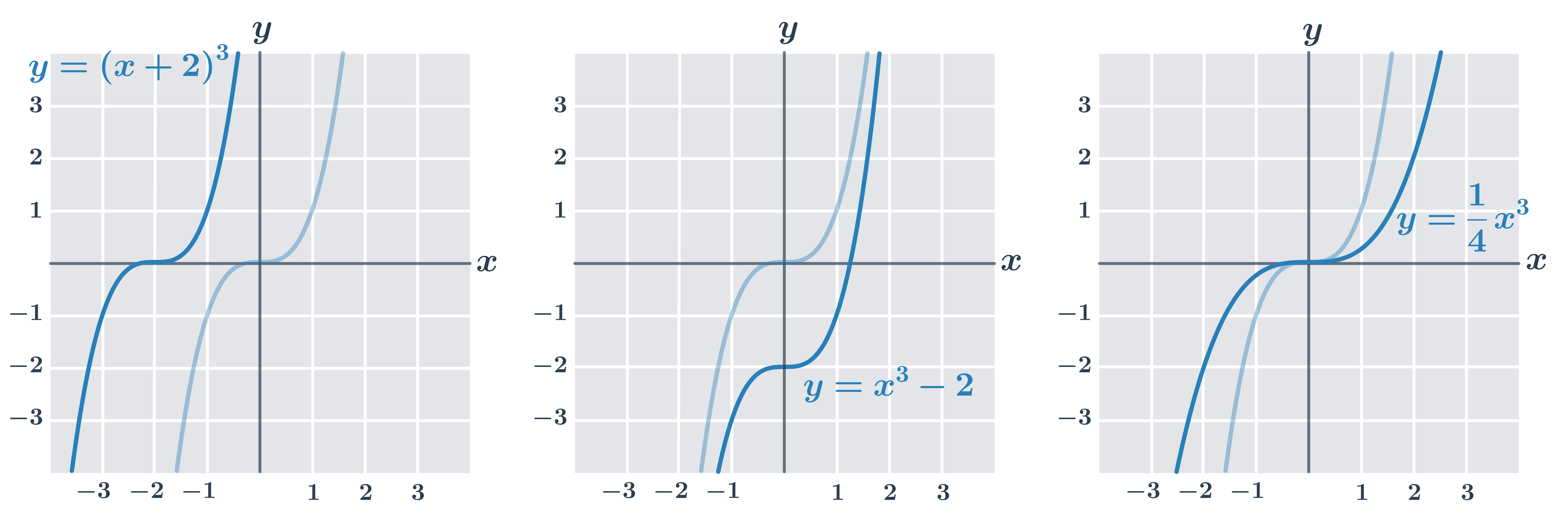
| y= (x+2)^3 | graf je posunutý v smere osi x |
| y=x^3-2 | graf je posunutý v smere osi y |
| y=\frac{1}{4} x^3 | graf bude natiahnutý alebo stlačený v smere osi y (v uvedenom grafe sa funkčné hodnoty zmenšia na štvrtinu, napríklad pre x=2 je hodnota funkcie y=\frac{1}{4} \cdot 2^3=2) |
Grafy goniometrických funkcií
Grafy základných goniometrických funkcií

Dopad úprav funkcie na graf

Obrázok ukazuje grafy niekoľkých úprav funkcie \sin(x).
| \sin(x+1) | graf má posunutú fázu (posun v smere osi x) |
| \sin(x)+1 | graf je posunutý v smere osi y |
| \sin(2x) | funkcia má zmenenú dĺžku periódy |
| 2\sin(x) | funkcia má zmenenú veľkosť amplitúdy |
Grafy exponenciálnych funkcií
Grafy exponenciálnych funkcií
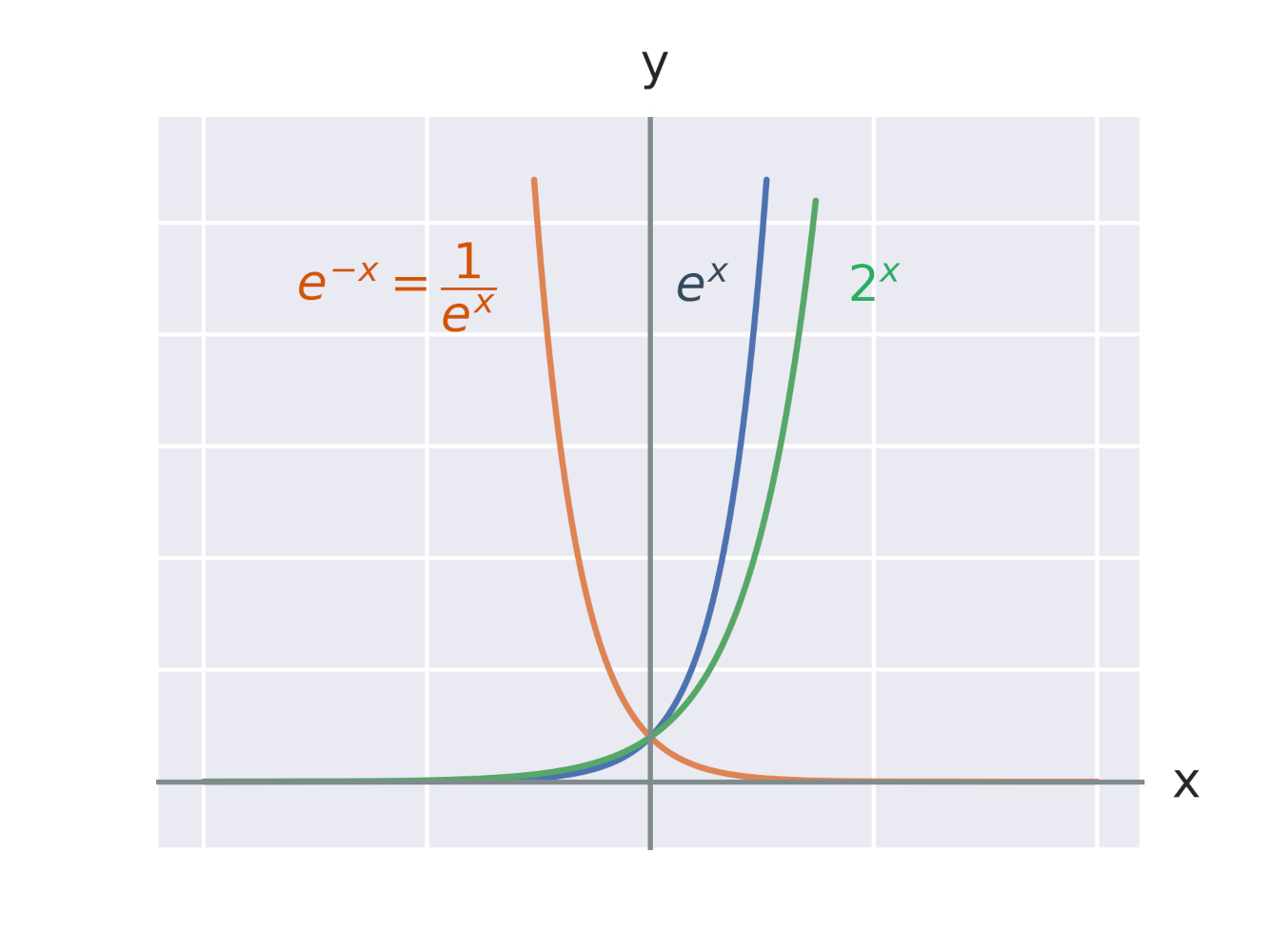
Grafom exponenciálnej funkcie je krivka s názvom exponenciála. Na obrázku sú grafy exponenciálnych funkcií so základmi 2 a e = 2{,}7 182 818 284\ldots. Vidíme tiež, že grafy funkcií e^x a e^{-x} sú spolu súmerné podľa osi y.
Efekt pripočítania konštanty k exponenciálnej funkcii
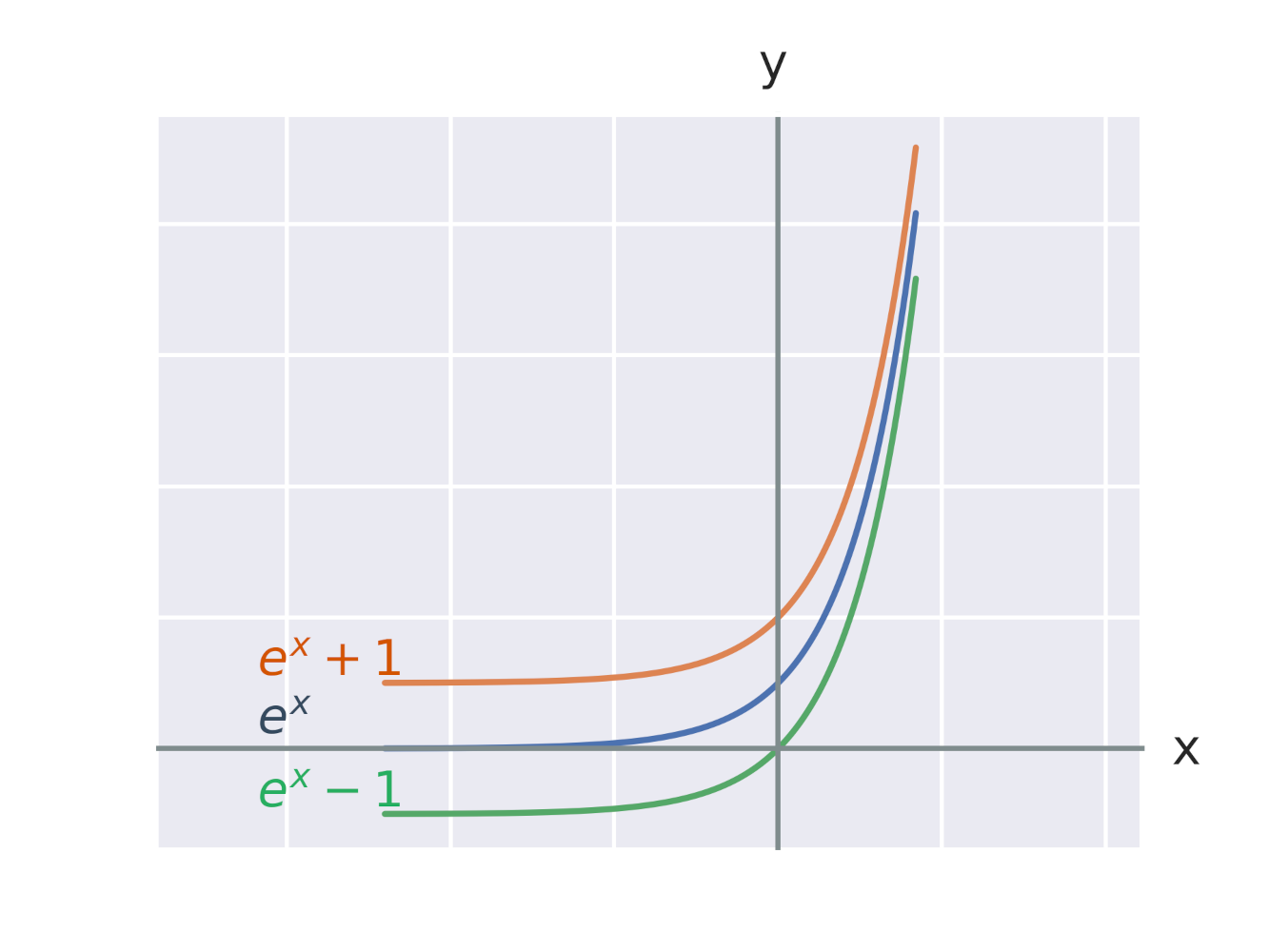
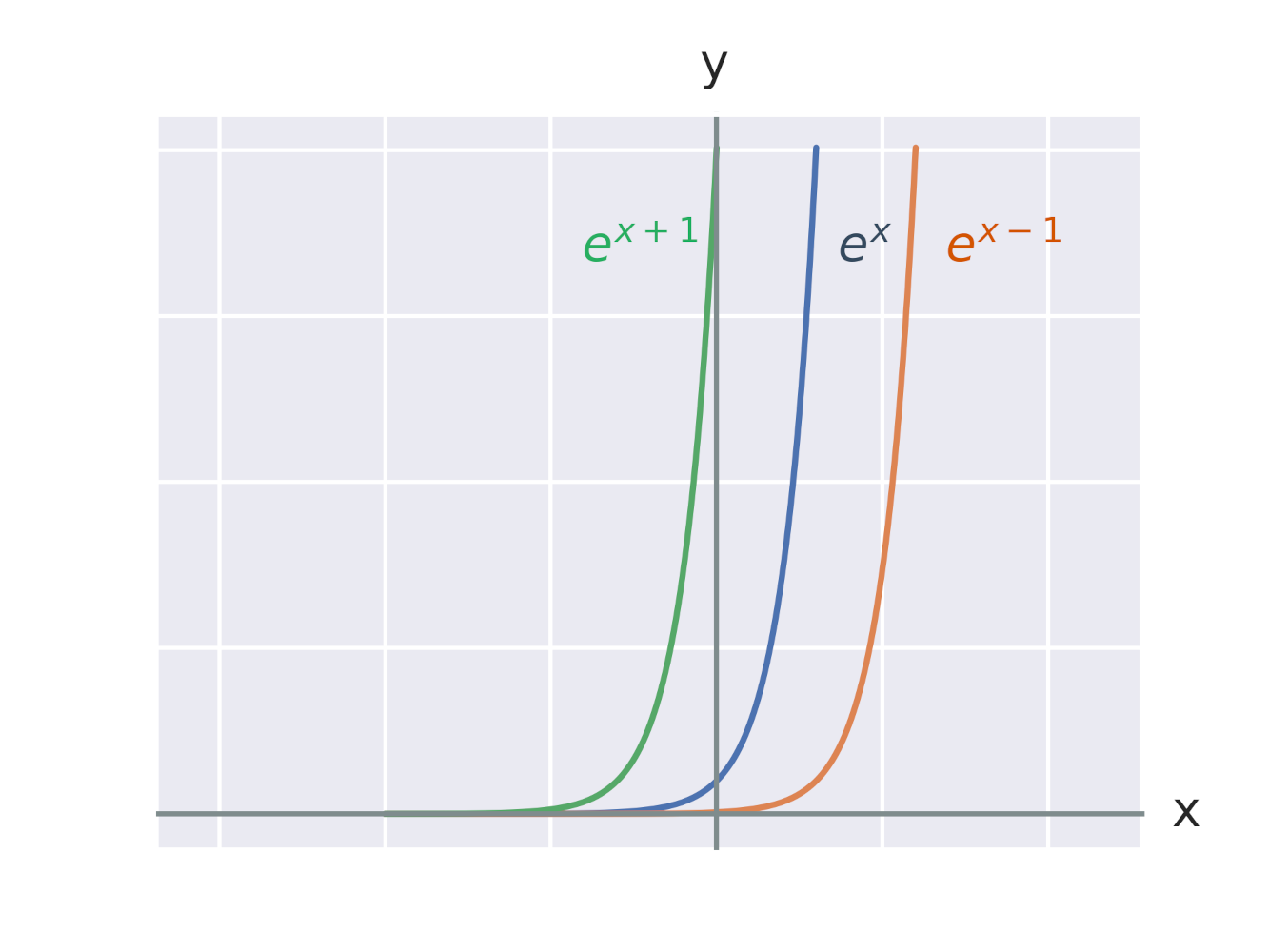
Efekt pripočítania konštanty k exponentu
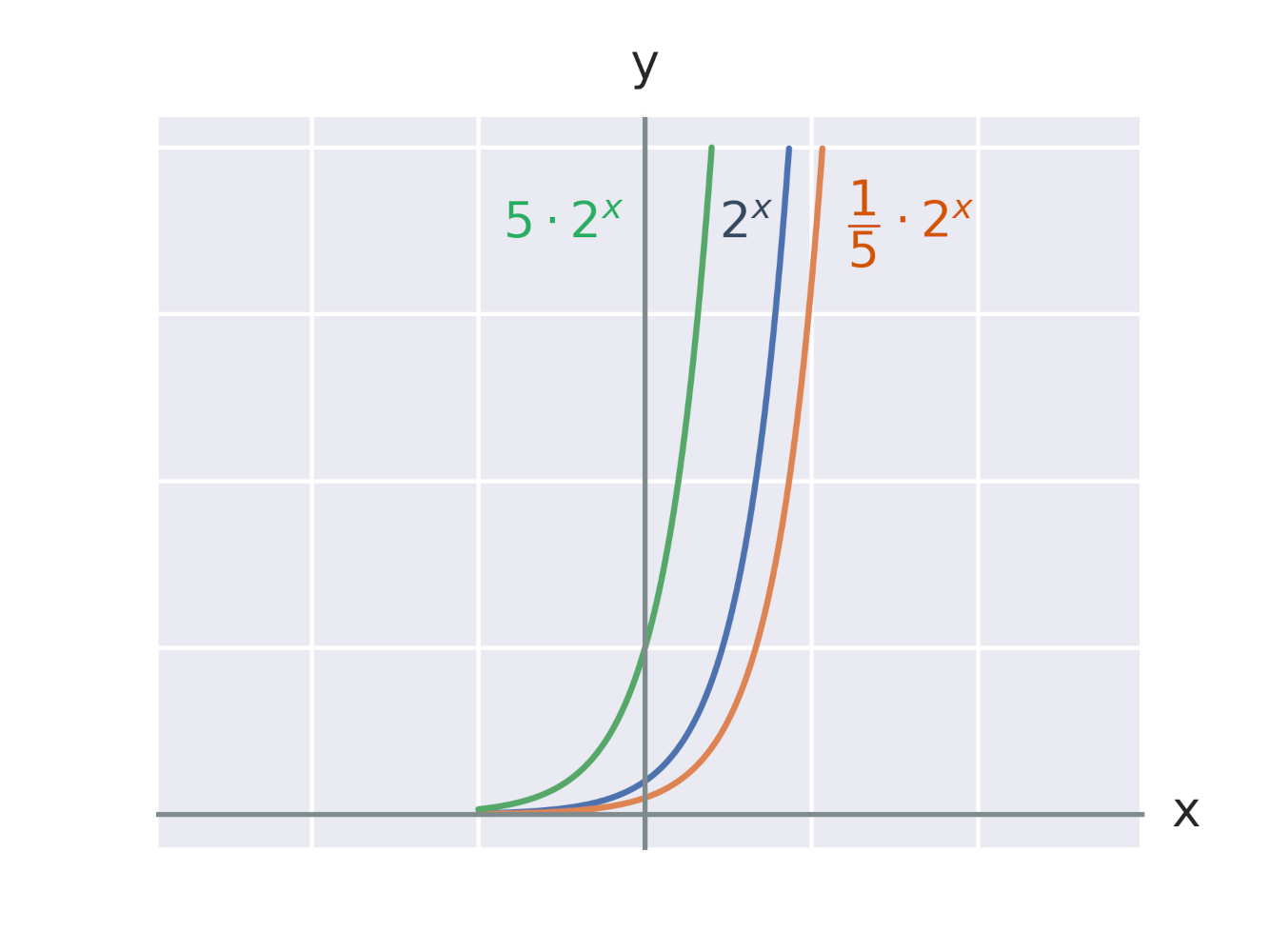
Efekt vynásobenia exponenciálnej funkcie konštantou
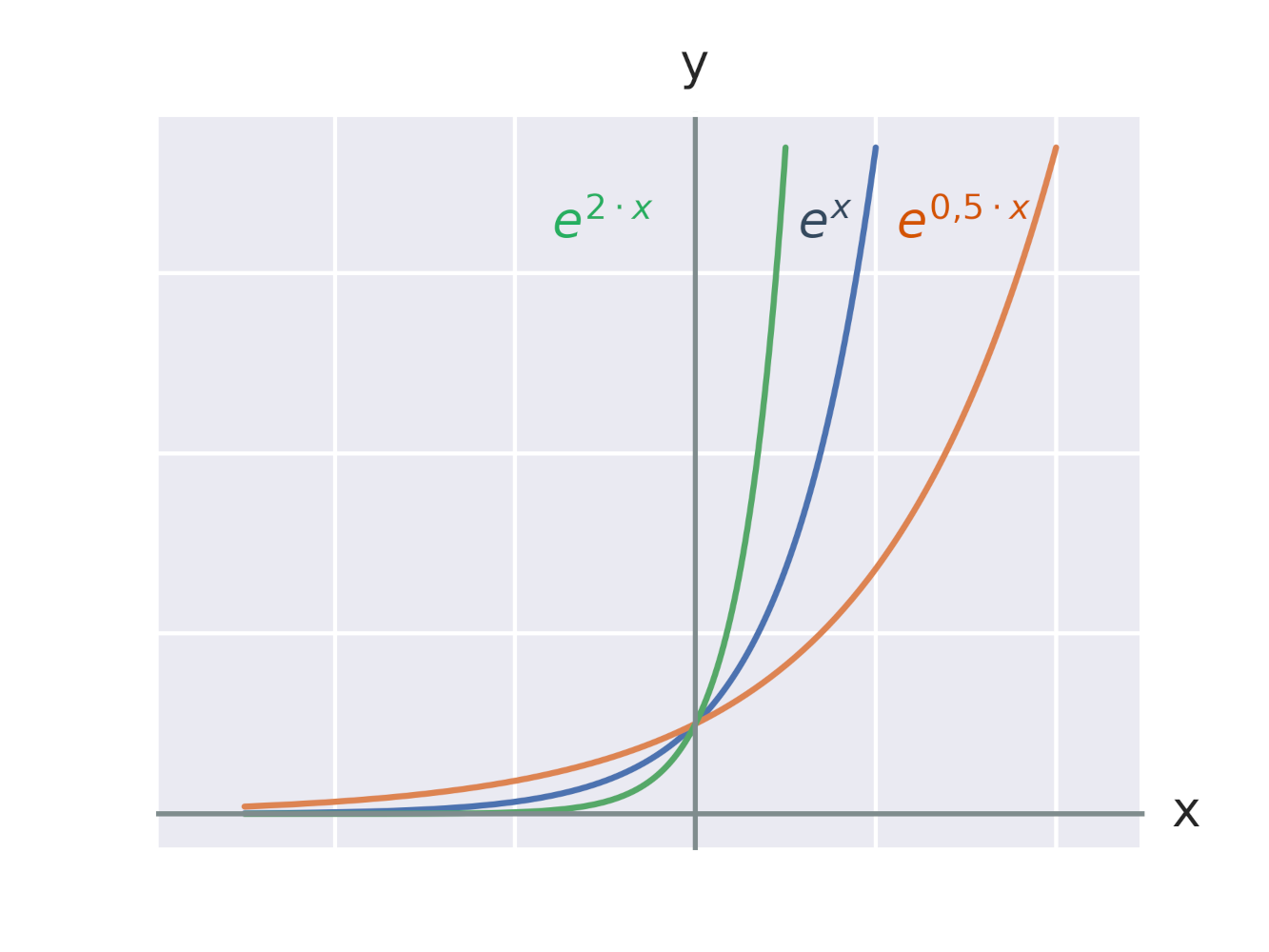
Efekt vynásobenia exponentu konštantou
Grafy logaritmických funkcií
Logaritmická funkcia je inverzná k exponenciálnej funkcii s rovnakým základom. Grafy dvoch navzájom inverzných funkcií sú osovo súmerné podľa osi prvého kvadrantu (teda priamky spĺňajúcej x=y).
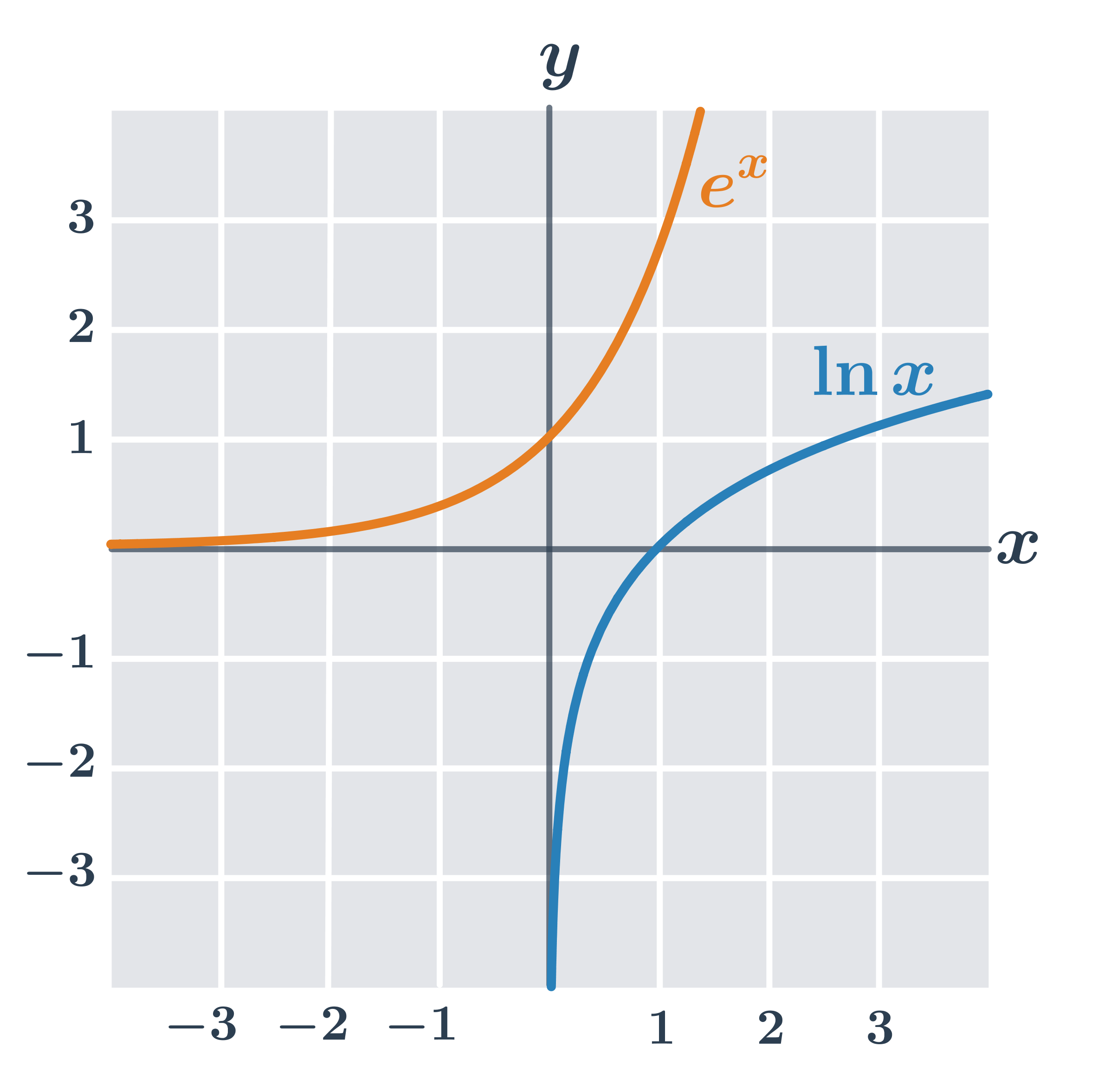
Na obrázku vidíme grafy logaritmických funkcií s rôznymi základmi 2, e, 10.
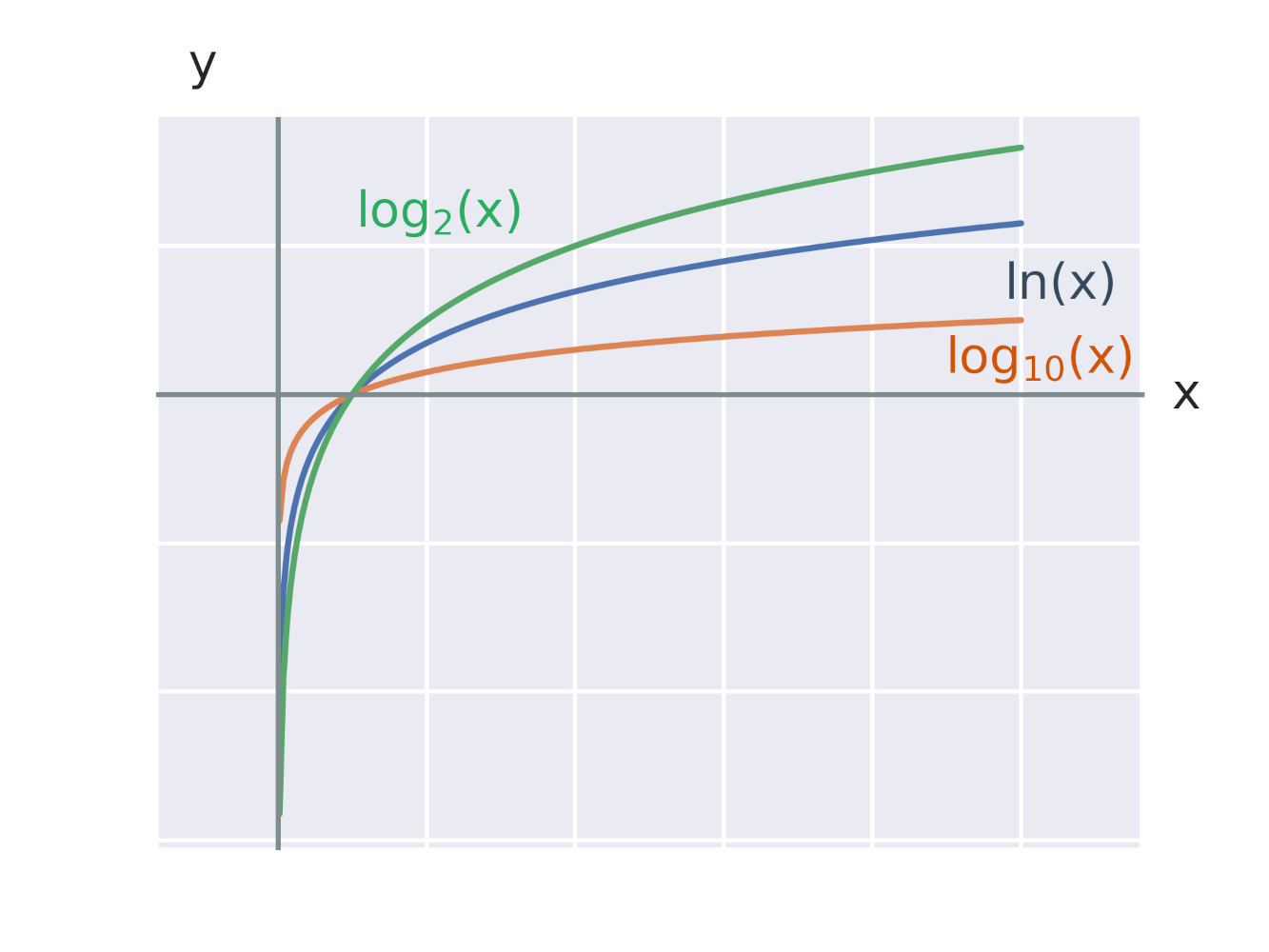
Značenie niektorých význačných logaritmických funkcií:
| funkcia | popis | značenie |
|---|---|---|
| \log_a x | všeobecne logaritmus x so základom a pre nejaké a >0, a\neq 1 | \log_a x |
| \log_e x | prirodzený logaritmus x | t u\ln x, v angl. textoch niekedy \log x |
| \log_{10} x | dekadický logaritmus x | tu \log x, v textoch slovenských aj angl. býva \log x, \log_{10}x |
| \log_2 x | binárny logaritmus x | tu \log_2 x, v textoch niekedy je aj \mathrm{lb}\;x |
Efekt pripočítania konštanty k logaritmickej funkcii
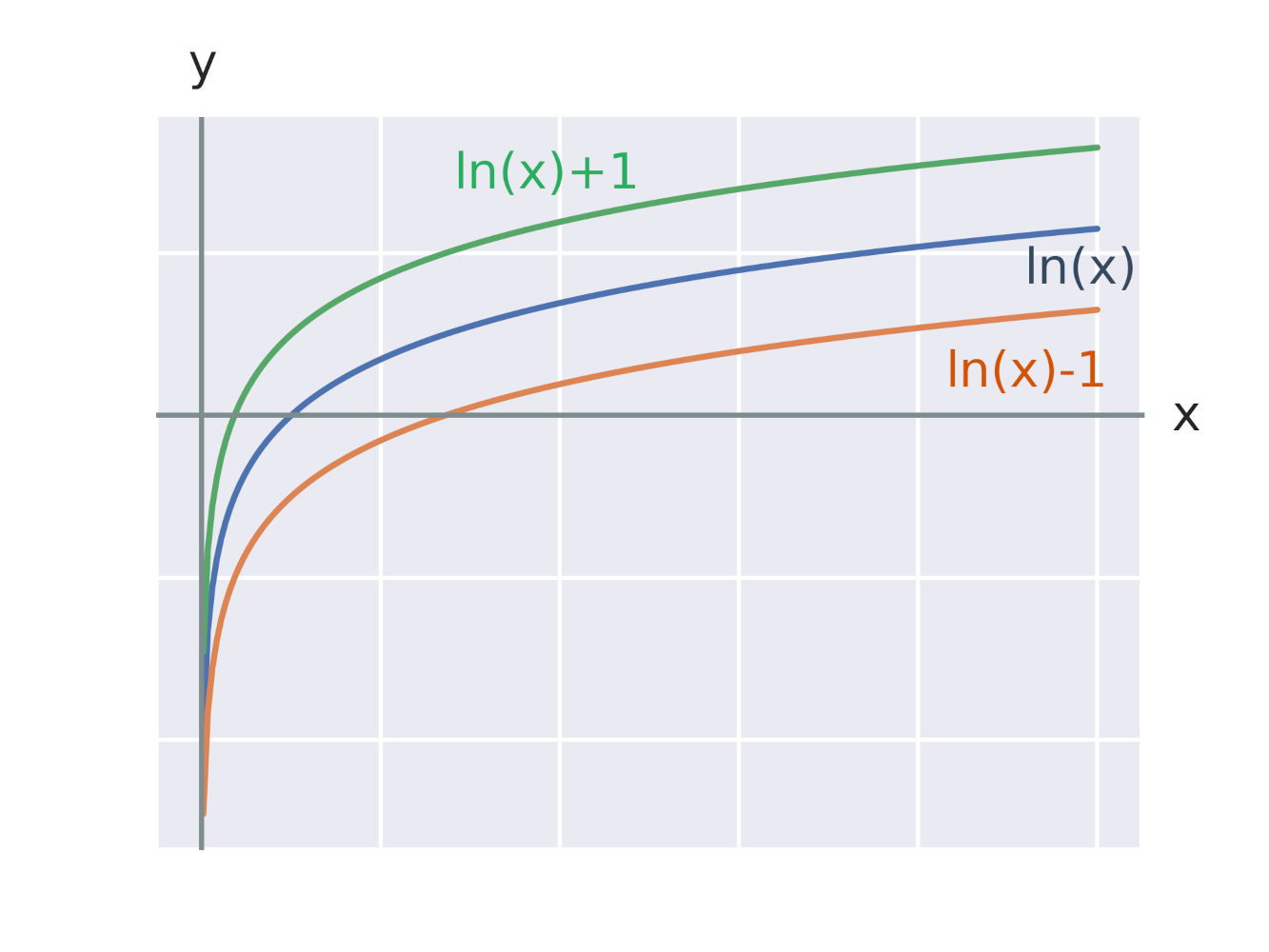
Efekt pripočítania konštanty k argumentu logaritmickej funkcie
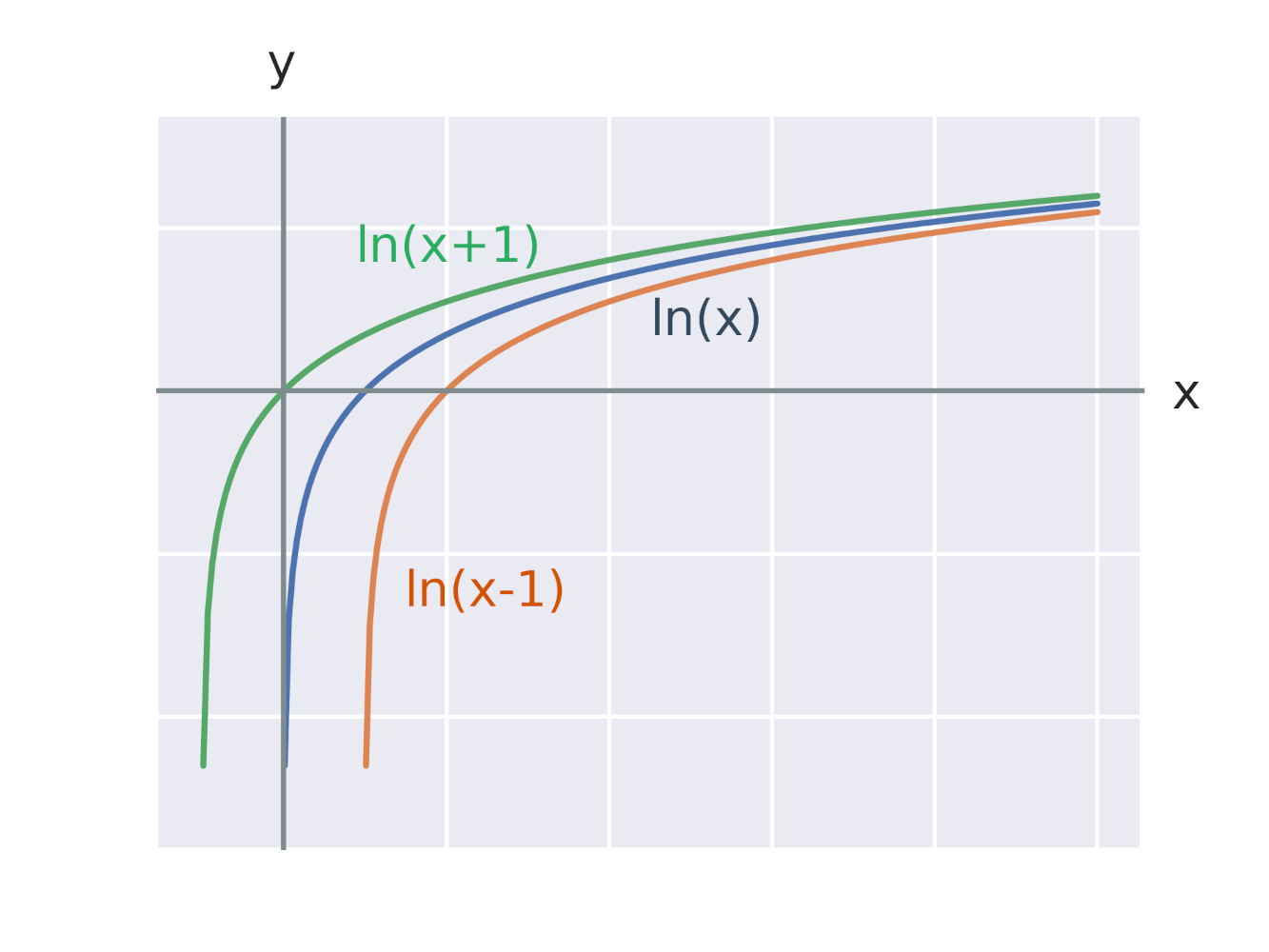
Efekt vynásobenia logaritmickej funkcie konštantou
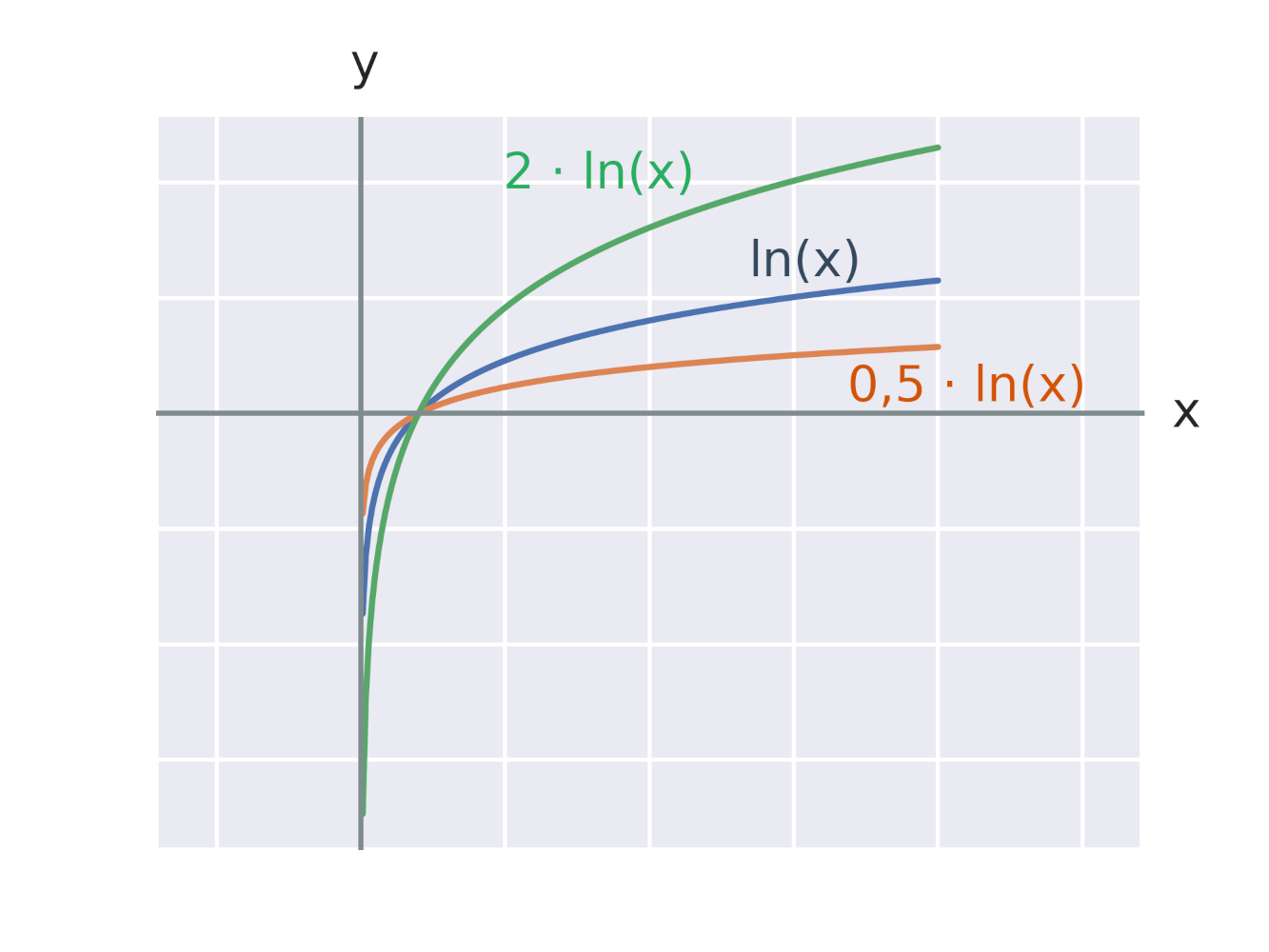
Efekt vynásobenie argumentu logaritmickej funkcie konštantou
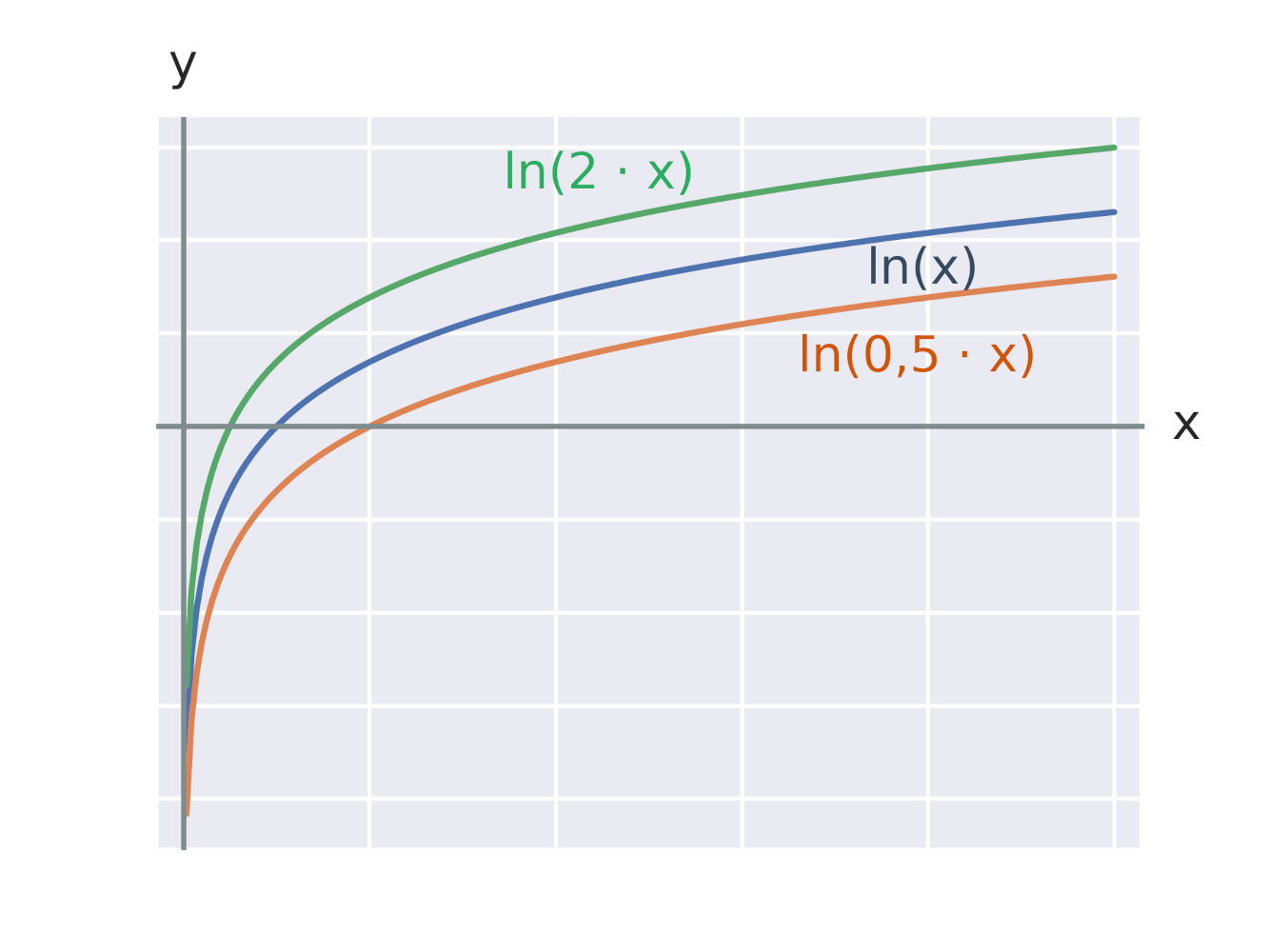
Grafy logaritmických funkcií
Logaritmická funkcia je inverzná k exponenciálnej funkcii s rovnakým základom. Grafy dvoch navzájom inverzných funkcií sú osovo súmerné podľa osi prvého kvadrantu (teda priamky spĺňajúcej x=y).

Graf každej logaritmickej funkcie tvaru y=\log_a x prechádza bodom [1,0], pretože pre ľubovoľnú konštantu a platí: \log_a 1=0. Na obrázku vidíme grafy logaritmických funkcií s rôznymi základmi 2, e, 10.

Značenie niektorých význačných logaritmických funkcií:
| funkcia | popis | ďalšie možné značenia |
|---|---|---|
| \log_a x | všeobecne logaritmus x so základom a pre nejaké a >0, a\neq 1 | |
| \ln x | prirodzený logaritmus x, teda logaritmus x so základom e | v angl. textoch niekedy \log x |
| \log x | dekadický logaritmus x, teda logaritmus x so základom 10 | \log_{10}x |
| \log_2 x | binárny logaritmus x, teda logaritmus x so základom 2 | niekedy sa objavuje \mathrm{lb}\;x |
Efekt pripočítania konštanty k logaritmickej funkcii

Efekt pripočítania konštanty k argumentu logaritmickej funkcie

Efekt vynásobenia logaritmickej funkcie konštantou

Efekt vynásobenia argumentu logaritmickej funkcie konštantou

Grafy lineárnych nerovníc
Grafom funkcie danej predpisom y= ax+b je priamka. Množinou riešení lineárnej nerovnice budú všetky body [x,y] ležiace v polrovine s hraničnou priamkou y= ax+b. Môže nastať jedna zo štyroch možností:
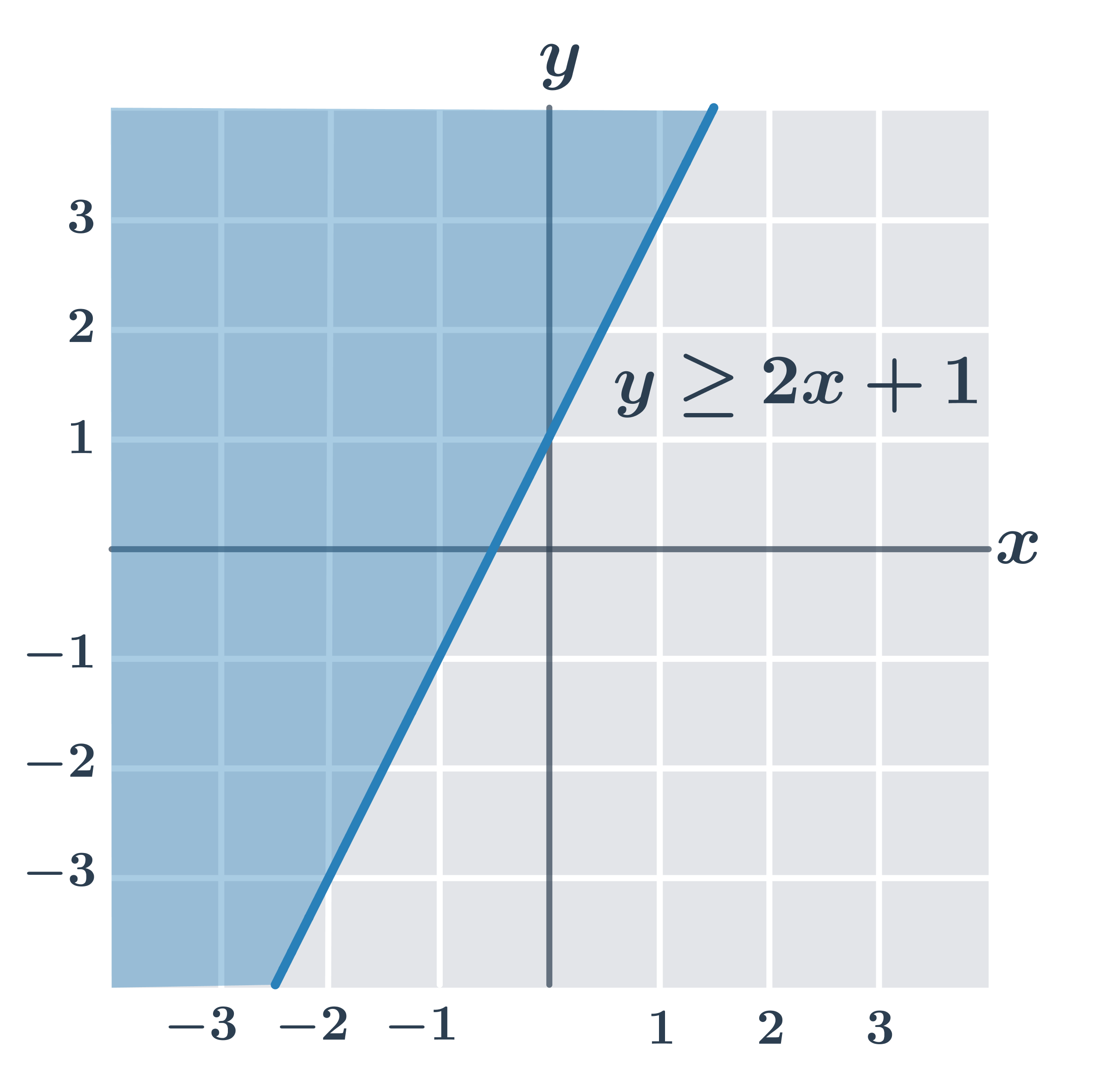
| y\geq ax+b | Nerovnosť spĺňajú všetky body v rovine, ktoré ležia priamo na priamke danej rovnicou y=ax+b alebo „nad“ touto priamkou (so súradnicou y väčšou než ax+b). |
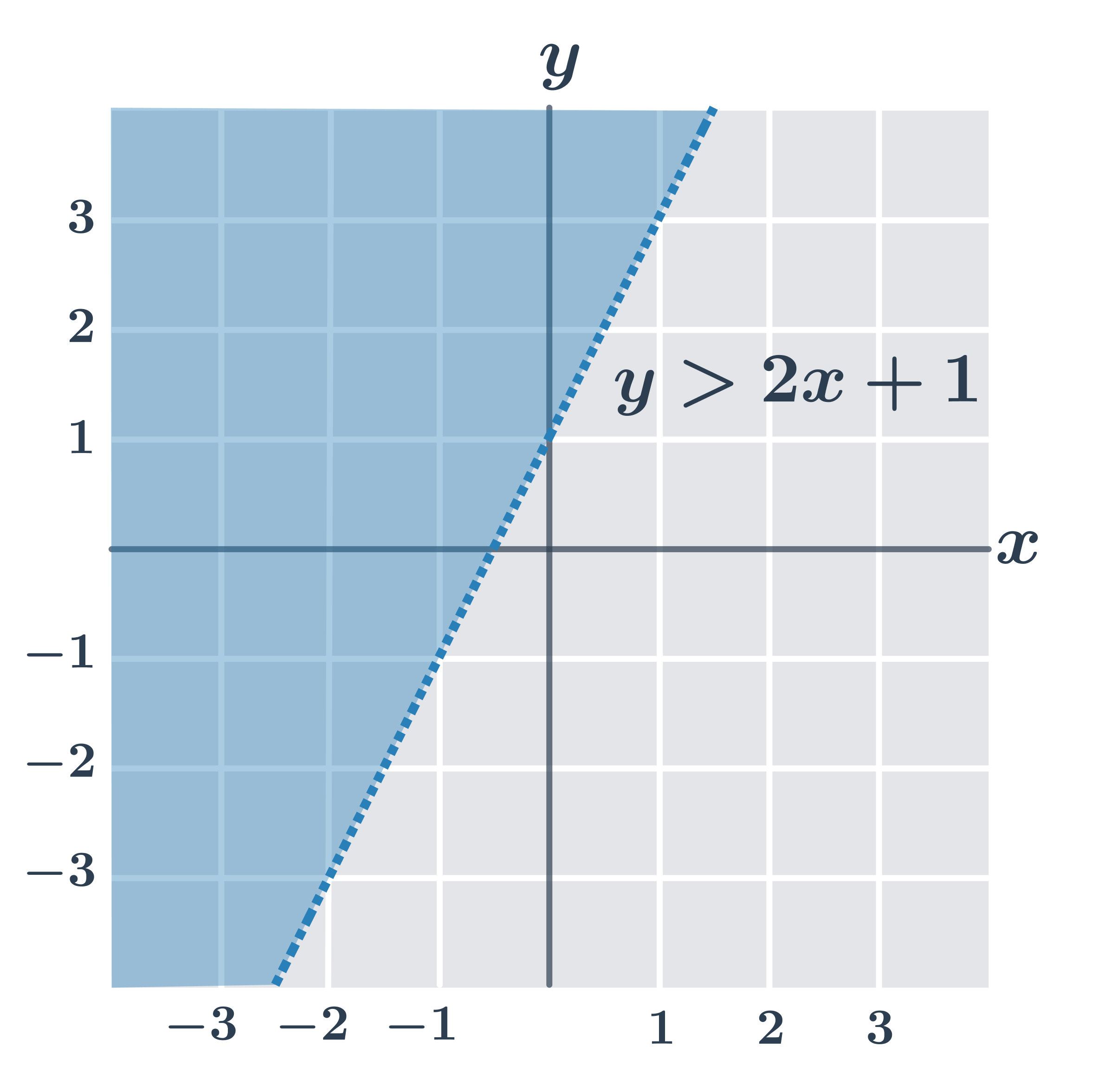
| y \gt ax+b | Nerovnosť spĺňajú všetky body v rovine, ktoré ležia „nad“ priamkou s rovnicou y=ax+b. |
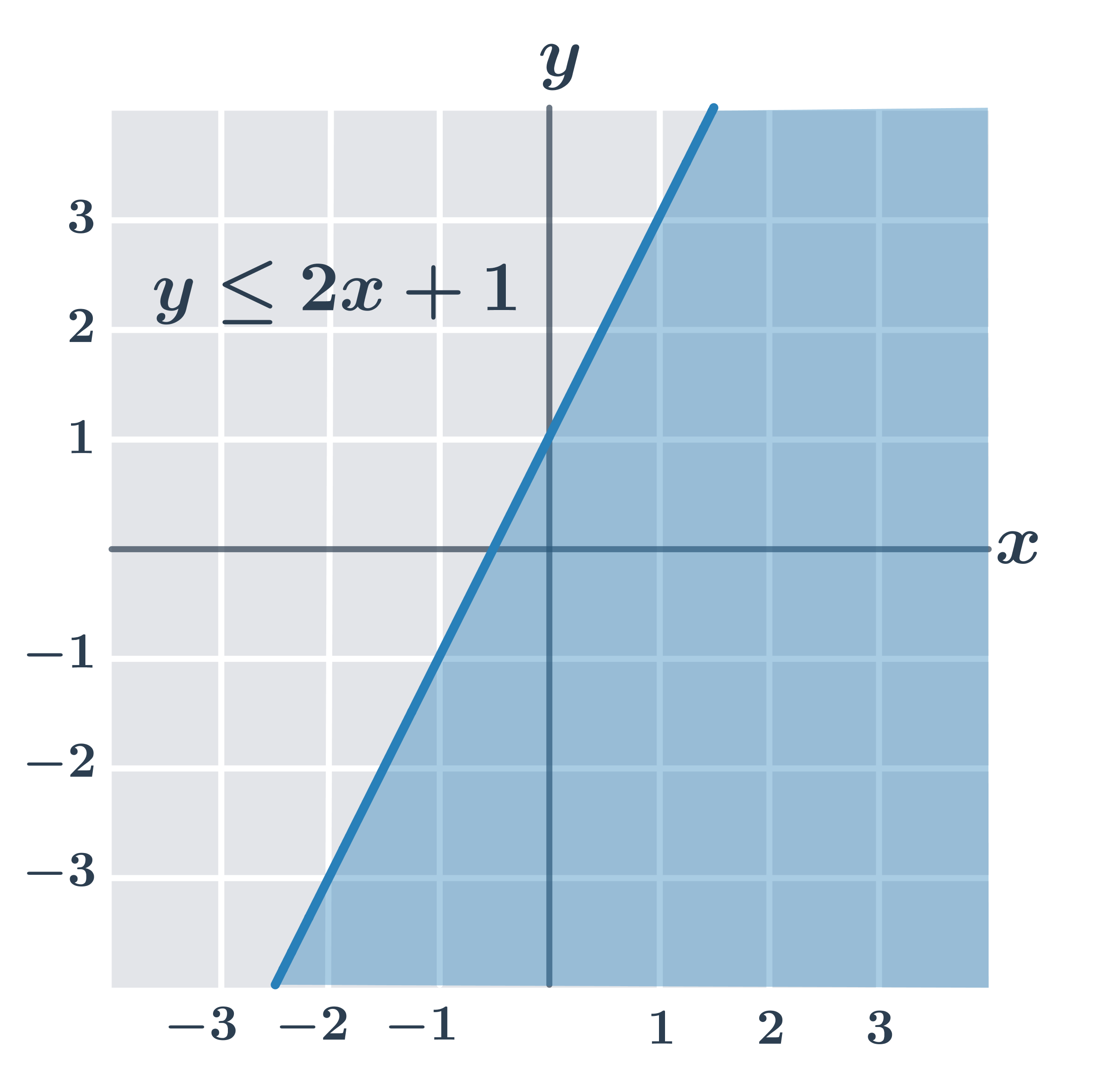
| y\leq ax+b | Nerovnosť spĺňajú všetky body v rovine, ktoré ležia na priamke s rovnici y=ax+b alebo „pod“ touto priamkou (so súradnicou y menšou než ax+b). |
| y \lt ax+b | Nerovnosť spĺňajú všetky body v rovine, ktoré ležia „pod“ priamkou s rovnicou y=ax+b. |
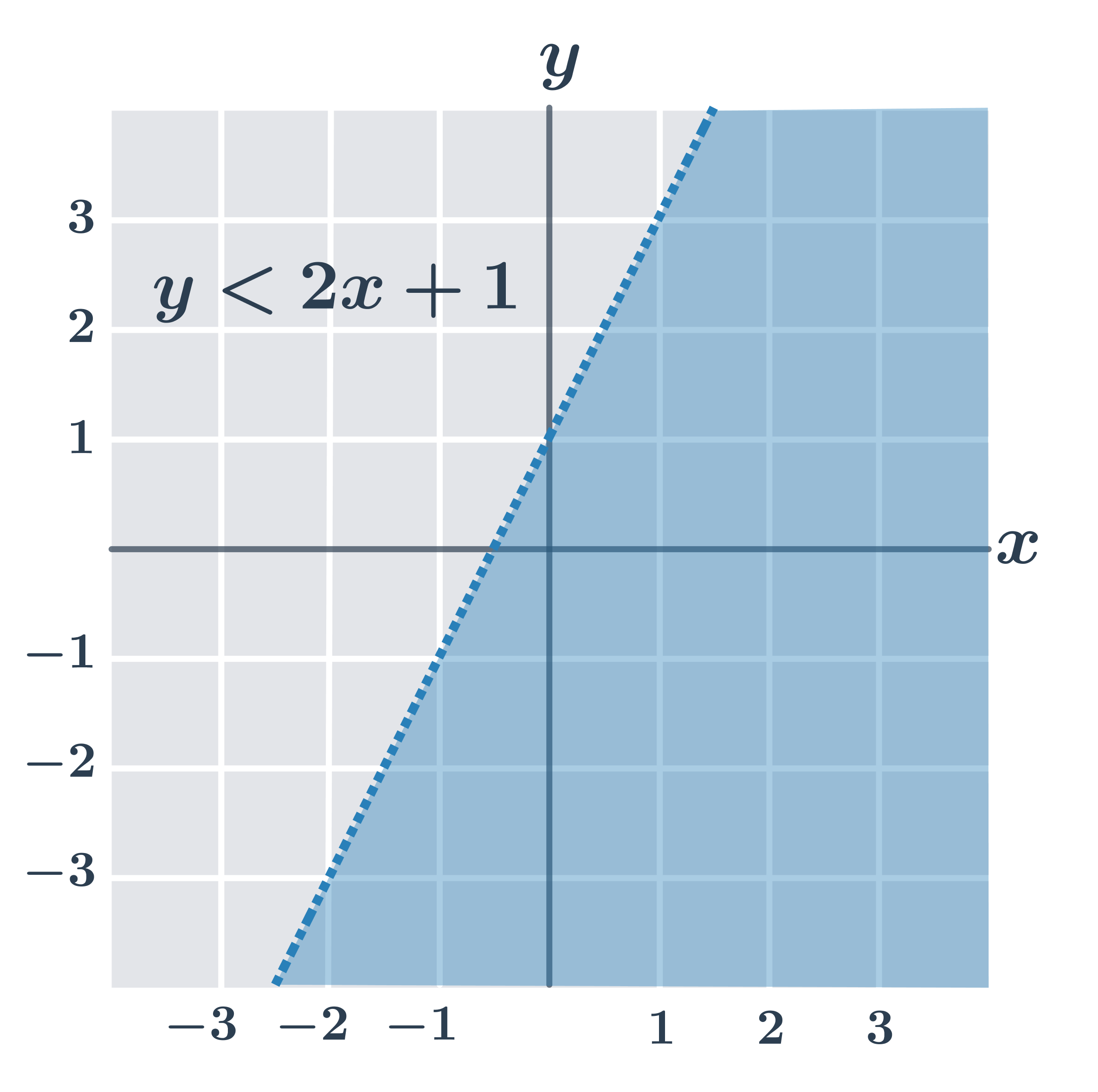
Na obrázkoch sú riešenia všetkých typov lineárnych nerovníc (všimnite si, že ak je v nerovnici iba znamienko \gt alebo \lt, body priamo na hraničnej priamke lineárnu nerovnicu nespĺňajú).
- y\geq 2x+1
- y \gt 2x+1
- y\leq 2x+1
- y \lt 2x+1