Výpis prehľadov
Mocniny, odmocniny, logaritmy
Prechádzate súhrny informácií k určitým témam. Systémy Vieme sa zameriavajú hlavne na ich precvičovanie. K cvičeniam k jednotlivým podtémam sa dostanete pomocou odkazov nižšie.
Podkapitoly
Mocniny, odmocniny, logaritmy
Umocňovanie je opakované násobenie. Napríklad 3^5 = 3\cdot 3\cdot 3\cdot 3\cdot 3 = 243. Odmocňovanie je opačnou operáciou k umocňovaniu. Napríklad druhá odmocnina z 36 je 6 (\sqrt{36}=6), pretože 6^2 = 6\cdot 6 = 36. Mocniny a odmocniny využívame v mnohých oblastiach matematiky, napríklad pri práci s mnohočlenmi, riešení kvadratických rovníc, výpočte obsahu a objemu alebo pri určovaní dĺžok strán v trojuholníku.
Prvým krokom pre zvládnutie tejto témy sú základné mocniny a odmocniny, kde pracujeme s malými, prirodzenými číslami. Pre tieto čísla sa vyplatí sa naučiť základné mocniny a odmocniny naspamäť, pretože na ne často v matematike narazíme.
Ako ďalší krok potrebujeme zvládnuť pracovať s výrazmi s mocninami a odmocninami.
Umocňovanie je možné definovať aj pre záporný mocniteľ. Tento spôsob umocňovania sa využíva na vedecký zápis čísel, ktorý nám umožňuje prehľadne pracovať s veľmi veľkými alebo veľmi malými číslami, vďaka čomu má hojné využitie vo fyzike.
Umocňovanie a odmocňovanie môžeme prirodzene používať aj v spojitosti so zlomkami a desatinnými číslami.
HoreMocniny sú skráteným zápisom opakujúceho sa násobenia. Príklady:
- 3^2 = 3\cdot 3 = 9
- 2^3 = 2\cdot 2 \cdot 2= 8
- 5^4 = 5\cdot 5\cdot 5\cdot 5 = 625
Pri umocňovaní záporných čísel je výsledok kladný pre párne mocniny, záporný pro nepárne mocniny.
- (-3)^2 = (-3)\cdot (-3) = 9
- (-3)^3 = (-3)\cdot (-3)\cdot (-3) = -27
- (-3)^4 = (-3)\cdot (-3)\cdot (-3)\cdot (-3) = 81
Nultá mocnina akéhokoľvek čísla je 1 (napr. 5^0=1, 564^0=1). Nula umocnená na ľubovoľné číslo je 0 (napr. 0^3 = 0\cdot 0\cdot 0 = 0). Čo poukazuje na zaujímavú otázku: Čomu sa rovná 0^0?
HoreOdmocniny
Odmocňovanie v matematike je čiastočne inverznou (opačnou) operáciou k umocňovaniu. Druhá odmocnina z čísla x je také nezáporné číslo a, pre ktoré platí a^2 = x. Druhú odmocninu značíme \sqrt{x}. Príklady:
- \sqrt{9} = 3, pretože 3^2 = 9
- \sqrt{25} = 5, pretože 5^2 = 25
- \sqrt{100} = 10, pretože 10^2 = 100
Všeobecne potom n-tá odmocnina z x je také číslo a, pre ktoré platí a^n = x, n-tú odmocninu značíme \sqrt[n]{x}. Príklady:
- \sqrt[3]{125} = 5, pretože 5^3 = 25
- \sqrt[5]{32} = 2, pretože 2^5 = 32
- \sqrt[4]{10 000} = 10, pretože 10^4 = 10 000
Odmocňovanie má aj geometrický význam. Ak máme štvorec s obsahom S, potom má tento štvorec dĺžku strany rovnú druhej odmocnine \sqrt{S}. Ak máme kocku s objemom V, potom má táto kocka dĺžku hrany rovnú tretej odmocnine \sqrt[3]{V}. Odmocniny často využijeme napríklad pri aplikácii Pytagorovej vety.
Graf funkcie odmocnina
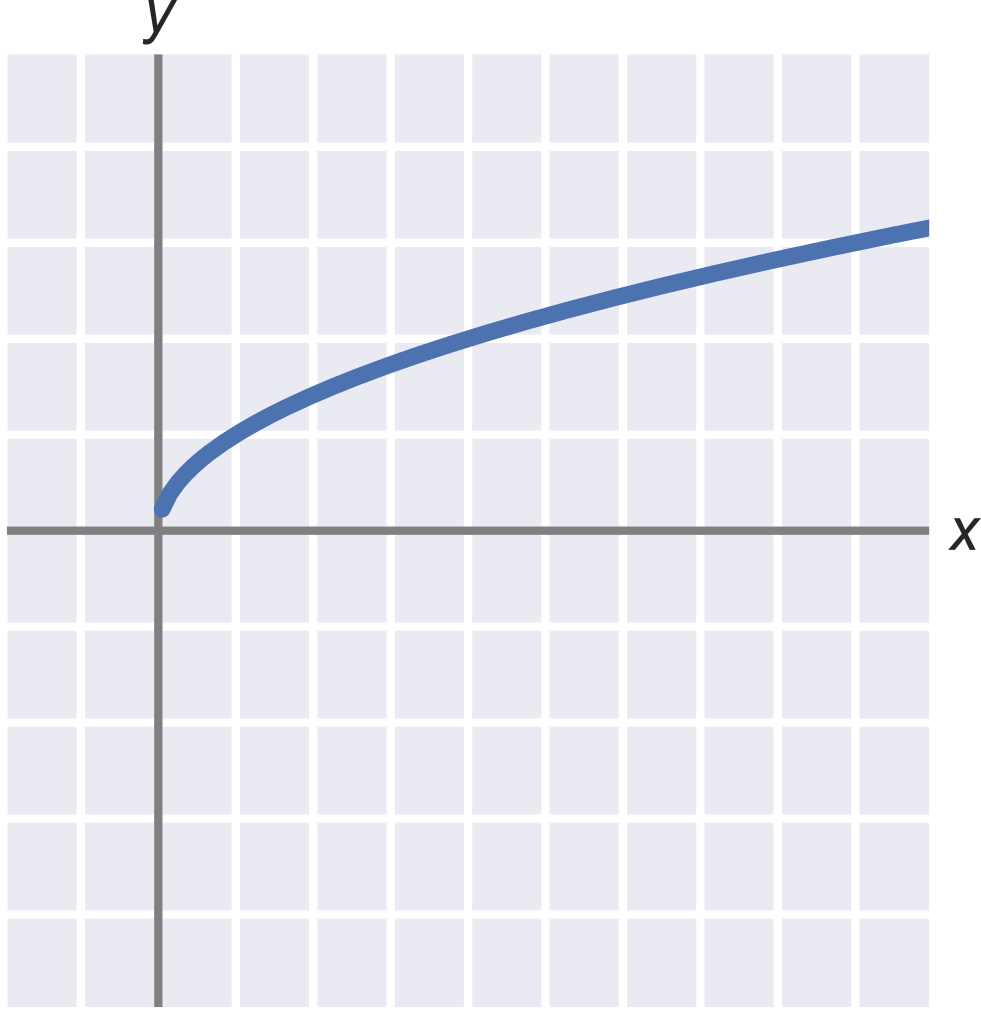
Odmocnina a záporné čísla
Keď hľadáme odmocninu napríklad z 25, tak hľadáme číslo, ktoré po umocnení dá 25. To spĺňa 5\cdot 5, ale tiež (-5)\cdot (-5). Odmocnina je však definovaná ako nezáporné číslo, takže \sqrt{25} = 5.
Druhú odmocninu môžeme počítať len z kladných čísel, pretože akékoľvek číslo umocnené na druhú je kladné. Odmocnina zo záporných čísel nie je definovaná. Alebo vlastne je, ale to musíme zaviesť komplexné čísla (čo je veľmi zaujímavý a užitočný nástroj, ale už trochu pokročilý, takže ho tu nebudeme rozoberať).
Pre bežné reálne čísla môžeme počítať odmocniny zo záporných čísel pre nepárne stupne n. Napríklad:
- \sqrt[3]{-8} = -2, pretože (-2)^3 = -8
- \sqrt[5]{-100 000} = -10, pretože (-10)^5 = -100 000
Výrazy s mocninami a odmocninami
Pre mocniny platia nasledujúce vzťahy:
- x^0 = 1
- x^a \cdot x^b = x^{a+b}
- x^a : x^b = x^{a-b}
- (x^a)^b = x^{a\cdot b}
- (x\cdot y)^a = x^a\cdot y^a
Konkrétne príklady, ktoré názorne ilustrujú, prečo uvedené vzťahy platia:
- 7^3\cdot 7^2 = (7\cdot 7\cdot7) \cdot (7\cdot 7) = 7^{3+2} = 7^5
- 6^4: 6^2 = (6\cdot 6\cdot 6\cdot 6) : (6\cdot 6) = 6^{4-2} = 6^2
- (5^3)^2 = (5\cdot 5\cdot 5)^2 = (5\cdot 5\cdot 5) \cdot (5\cdot 5\cdot 5) = 5^{3\cdot 2} = 5^6
- (7\cdot 8)^3 = (7\cdot 8) \cdot (7\cdot 8) \cdot (7\cdot 8) = (7\cdot 7\cdot 7) \cdot (8\cdot 8\cdot 8) = 7^3 \cdot 8^3
Pre odmocniny platia nasledujúce vzťahy (predpokladáme x, y > 0):
- \sqrt{0} = 0
- \sqrt{1} = 1
- \sqrt{x}\cdot \sqrt{x} = x
- \sqrt{xy} = \sqrt{x} \cdot \sqrt{y}
- \sqrt{\frac{x}{y}} = \frac{\sqrt{x}}{\sqrt{y}}
- \sqrt[n]{x^k} = x^{\frac{k}{n}}
- \sqrt[n]{\sqrt[m]{x}} = \sqrt[n\cdot m]{x}
Príklady:
- \sqrt{24} = \sqrt{4\cdot 6} = \sqrt{4} \cdot \sqrt{6} = 2\sqrt{6}
- \sqrt{3} \cdot \sqrt{3} = (\sqrt{3})^2 = 3
- \sqrt[3]{5^6} = 5^\frac63 = 5^2 = 25
Záporné mocniny
Mocnina so záporným exponentom zodpovedá prevrátenej hodnote príslušnej mocniny s kladným exponentom. Teda x^{-n} = \frac{1}{x^n}. Toto pravidlo je dôsledkom vlastnosti násobenia x^n\cdot x^m = x^{n+m}. Musí teda platiť x^{-n} \cdot x^n = x^{-n+n} = x^0 = 1.
Príklady:
- 2^{-1} = \frac{1}{2} = 0,5
- 2^{-2} = \frac{1}{2^2} = \frac{1}{4} = 0,25
- 10^{-2} = \frac{1}{10^2} = 0,01
- 0,5^{-1} = 2^1 = 2
Vedecký zápis čísel
Vedecký zápis čísel je zápis čísel pomocou súčinu m\cdot 10^n, kde m je reálne číslo (mantisa) a 10^n je mocnina desiatky. Tento zápis čísel je užitočný hlavne pri práci s veľmi veľkými alebo veľmi malými číslami. Napríklad hmotnosť Zeme je približne 5 970 000 000 000 000 000 000 000 kg, čo je ďaleko prehľadnejšie v zápise 5{,}97\cdot 10^{24} kg. Príklady:
| 5 | 5\cdot 10^0 |
| 0,4 | 4\cdot 10^{-1} |
| 8100 | 8{,}1\cdot 10^{3} |
| 0,032 | 3{,}2\cdot 10^{-2} |
| 8 713 000 000 | 8{,}713\cdot 10^{9} |
| 0,000 000 009 52 | 9{,}52\cdot 10^{-9} |

