Výpis prehľadov
Obsah
Podkapitoly
Obsah trojuholníka
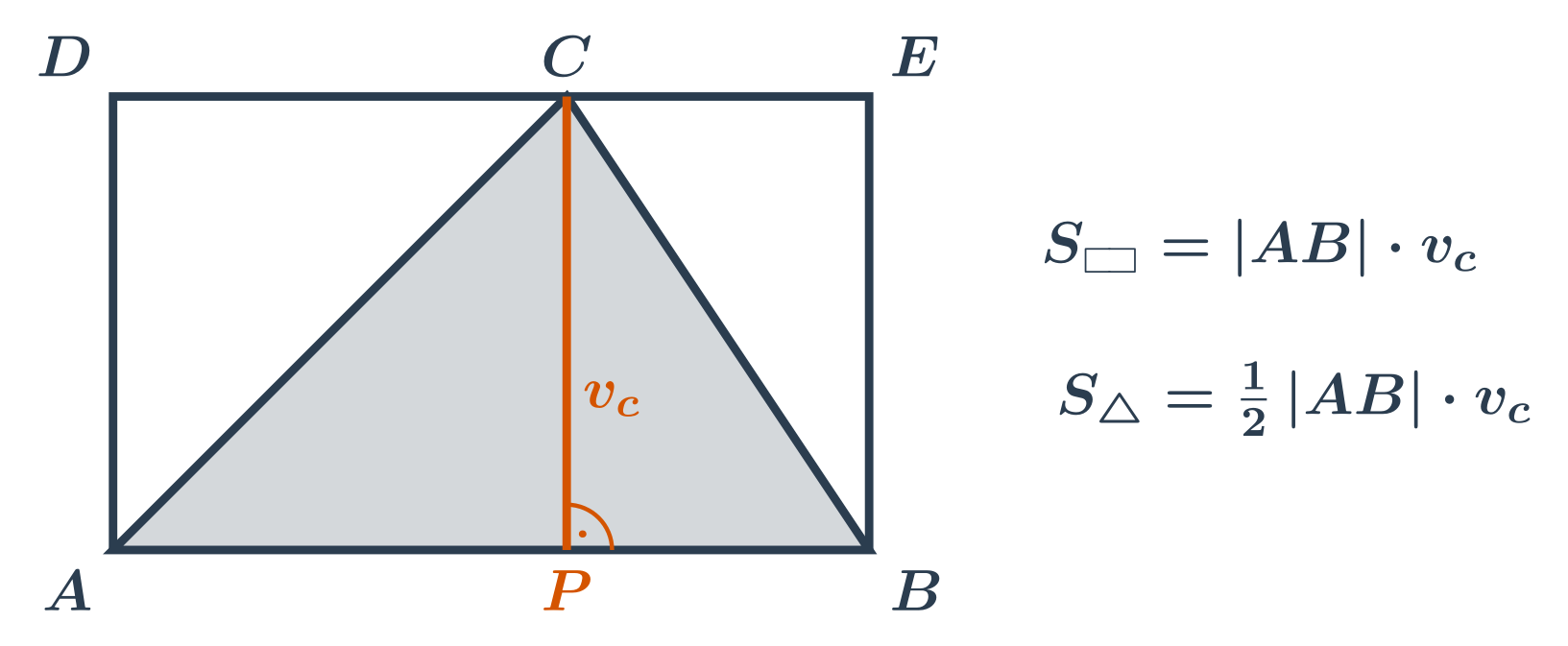
Obsah trojuholníka vypočítame ako súčin dĺžky ľubovoľnej strany trojuholníka a výšky príslušnej k tejto strane, takže: S_{\triangle} = \frac12 \cdot a \cdot v_a = \frac12 \cdot b \cdot v_b = \frac12 \cdot c \cdot v_c
Čo si môžeme predstaviť ako polovicu obsahu obdĺžnika, v ktorom je náš trojuholník takto vpísaný:
Príklady k obsahu:
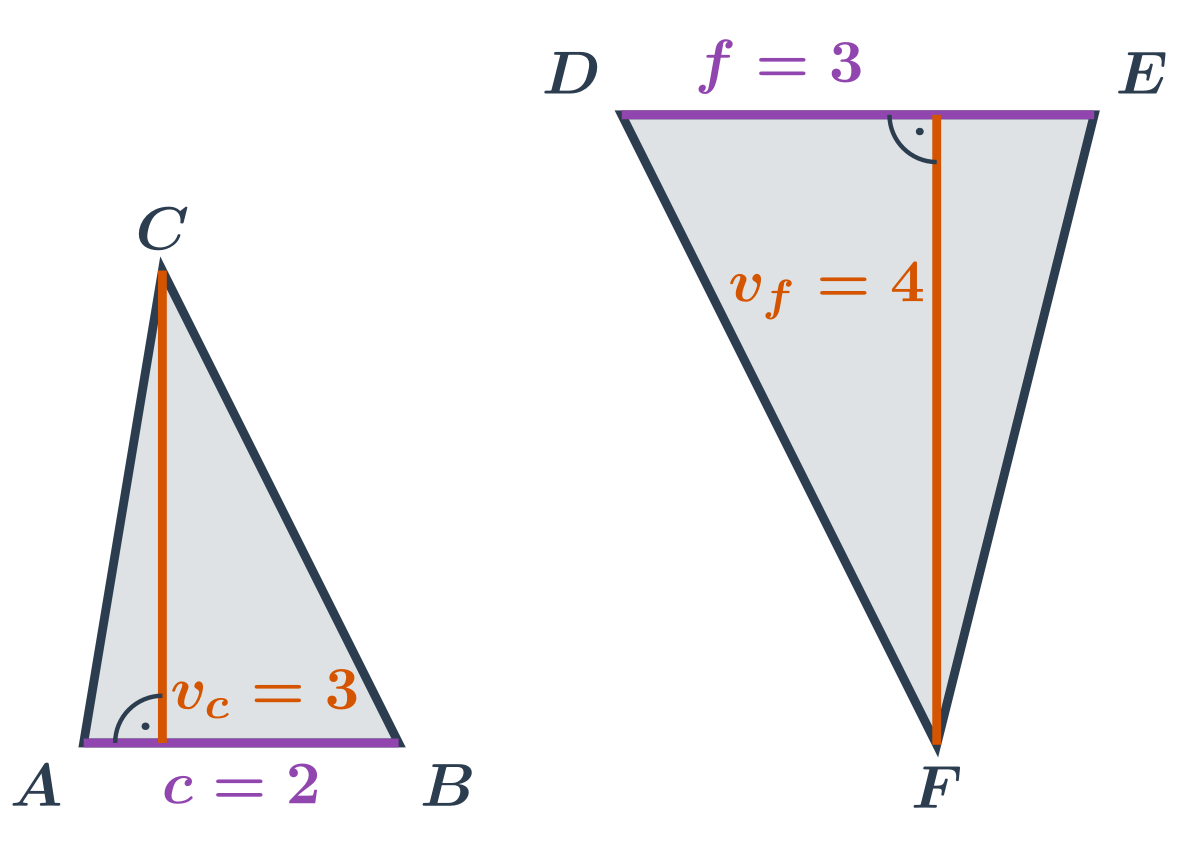
- Trojuholník ABC: Dĺžka strany \left| AB \right| je 2. Veľkosť k nej príslušnej výšky v_c je 3. Obsah trojuholníka ABC je rovný \frac12 \cdot 2 \cdot 3 = 3.
- Trojuholník DEF: Nevadí nám, že trojuholník na náčrtku vyzerá zvláštne natočený. Poznáme dĺžku strany \left| DE \right|, čo je 3. Veľkosť k nej príslušnej výšky v_f je 4. Obsah trojuholníka DEF je rovný \frac12 \cdot 3 \cdot 4 = 6.
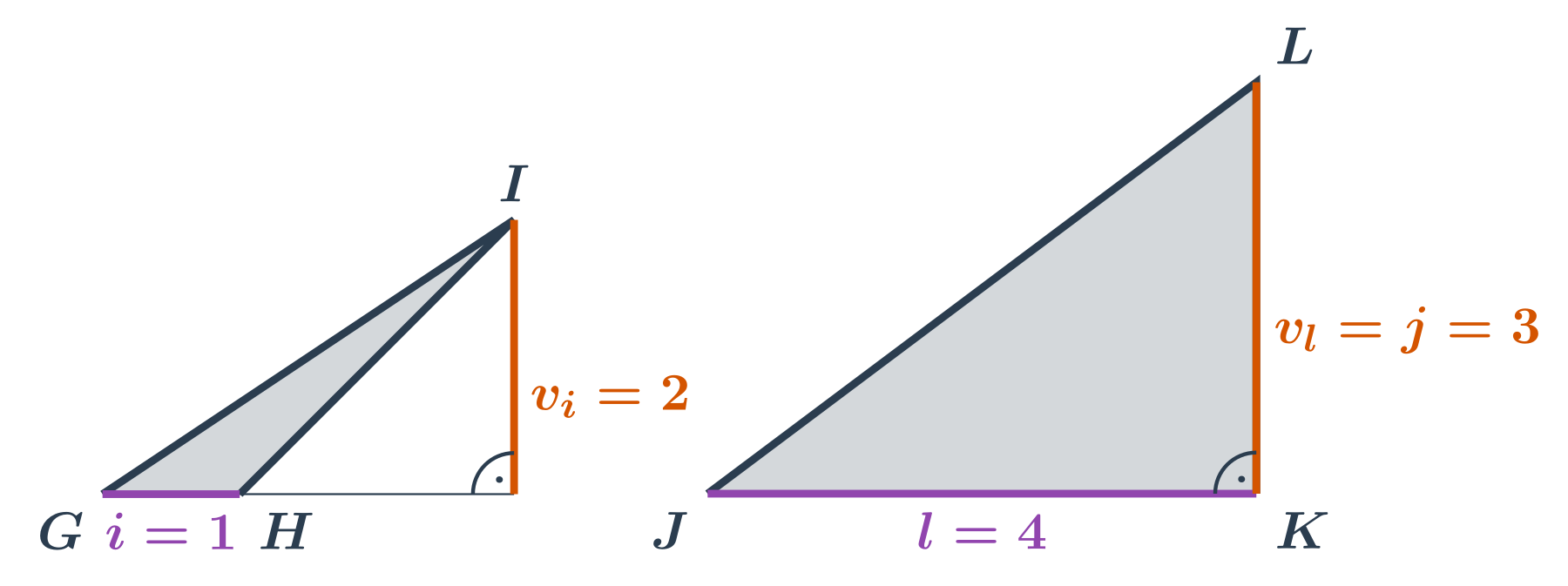
- Trojuholník GHI: Nevadí nám ani keď je päta kolmice, na ktorej leží výška, mimo stranu trojuholníka. Dĺžka strany \left| GH \right| je 1. Veľkosť k nej príslušnej výšky v_i je 2. Obsah trojuholníka GHI je \frac12 \cdot 2 \cdot 1 = 1.
- Trojuholník JKL: S pravouhlým trojuholníkom si tiež poradíme. Dĺžka strany \left| JK \right| je 4. Veľkosť k nej príslušnej výšky v_l je 3 (a je to zároveň aj dĺžka strany KL nášho trojuholníka). Obsah trojuholníka JKL je \frac12 \cdot 4 \cdot 3 = 6.
Obsah štvorca a obdĺžnika
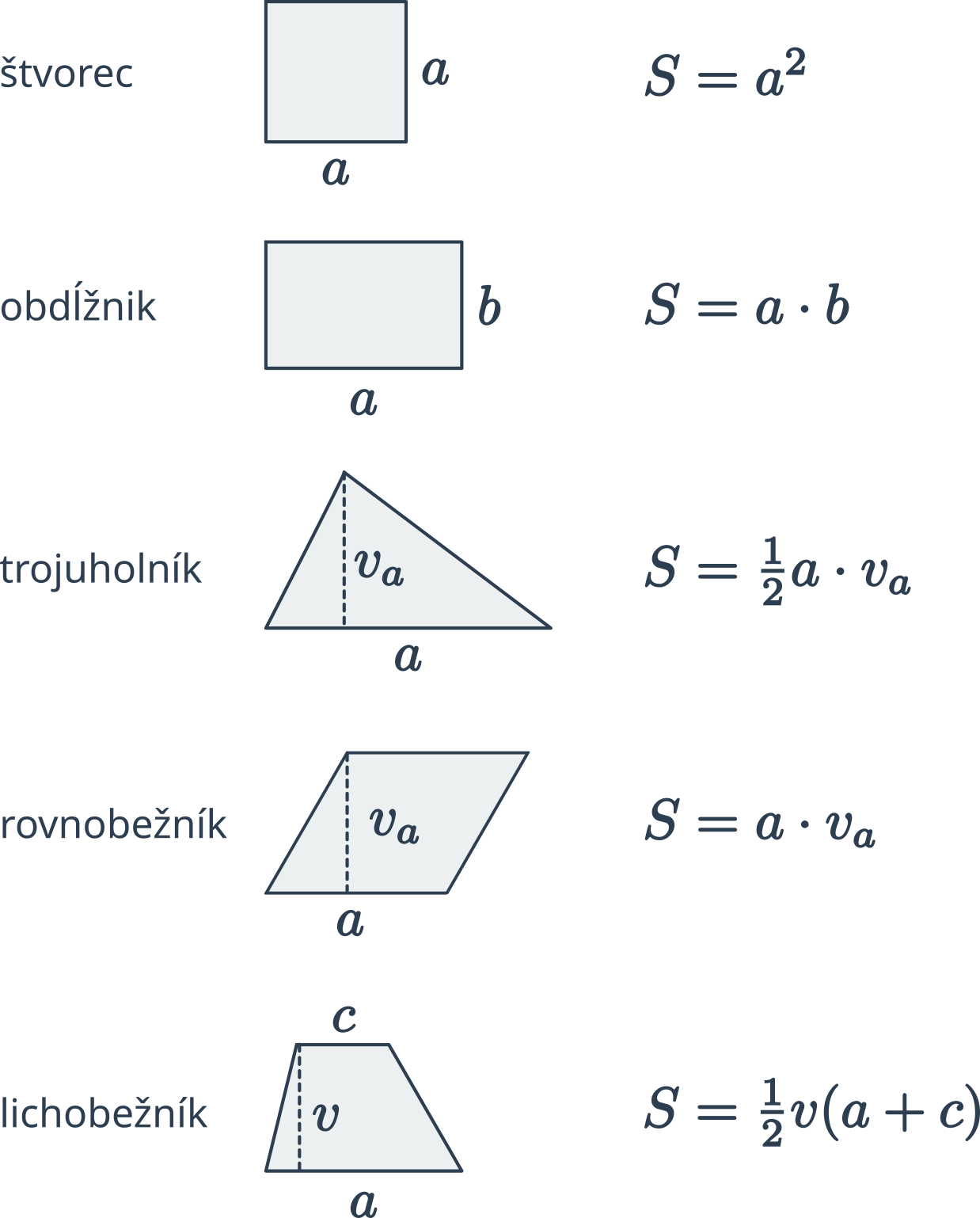
Obsah štvorca so stranou dĺžky a je S=a\cdot a=a^2.
Obsah obdĺžnika so stranami s dĺžkami a,b je rovný S=a\cdot b.
HoreObsah rovnobežníka
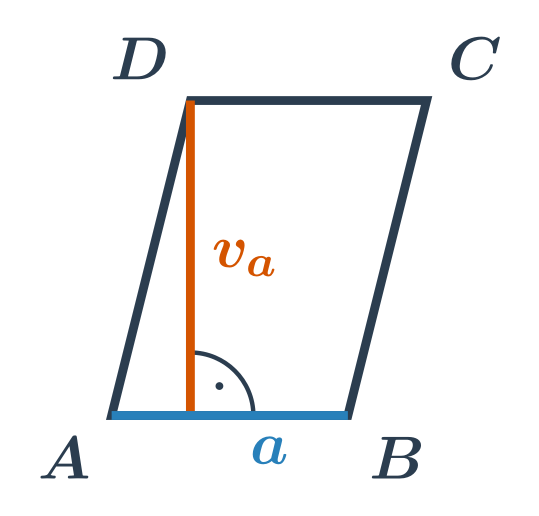
Obsah rovnobežníka, v ktorom k strane s dĺžkou a patrí výška v_a, vypočítame ako S= a\cdot v_a.
Obsah lichobežníka
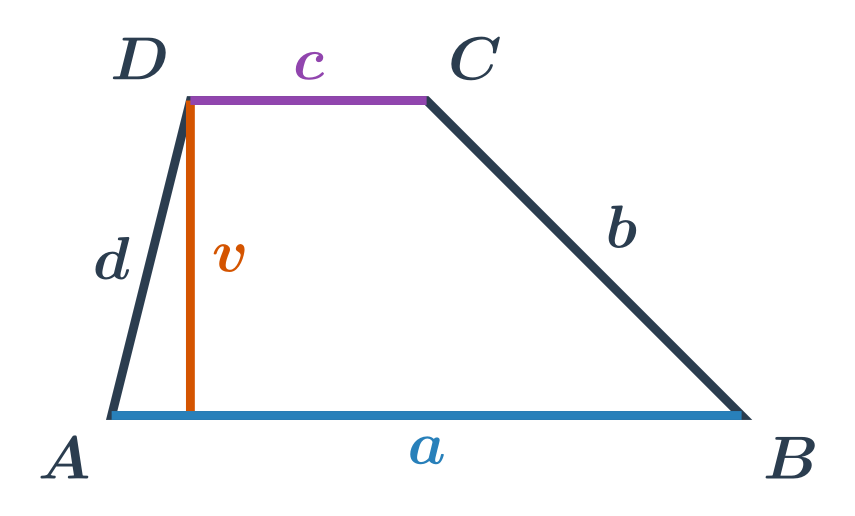
Obsah lichobežníka so základňami s dĺžkami a,c a výškou v vypočítame podľa vzorčeka S=\frac{1}{2} \cdot (a+c) \cdot v.
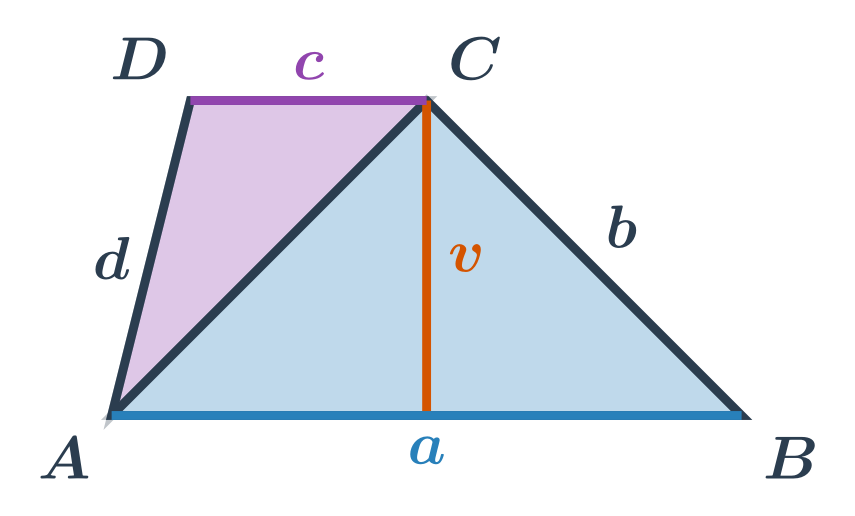
Intuíciu za týmto vzorčekom je vidieť na nasledujúcom obrázku. Obsah lichobežníka je rovný súčtu obsahov dvoch trojuholníkov.
- Prvý trojuholník má výšku v príslušnú k strane dĺžky a. Jeho obsah je S_{ABC}=\frac{1}{2} \cdot a \cdot v.
- Druhý trojuholník má výšku v príslušnú k strane dĺžky c. Jeho obsah je S_{ACD}=\frac{1}{2} \cdot c \cdot v.
Súčet obsahov týchto dvoch trojuholníkov je S = S_{ABC} + S_{ACD} = \frac{1}{2} \cdot a \cdot v + \frac{1}{2} \cdot c \cdot v = \frac{1}{2} \cdot (a+c) \cdot v
Obsah kruhu
Vzorce
Obvod kruhu (aj kružnice) s polomerom r je o=2\pi r. Pre priemer d platí o = \pi d.
Obsah kruhu s polomerom r je S=\pi r^2. Pre priemer d platí S = \frac{1}{4} \pi d^2.
Konštanta \pi sa nazýva tiež Ludolfovo číslo. \pi je iracionálne číslo, čo znamená, že ho nie je možné vyjadriť zlomkom ani zapísať presne v desiatkovej sústave. Približná hodnota \pi je 3,141 592 65.
Pri výpočte obsahu a obvodu kruhu dávame dobrý pozor na to, či vychádzame zo znalosti polomeru alebo priemeru. Zámena priemeru za polomer je častou chybou.
Intuícia
Základnú intuíciu za vzorcami na výpočet obsahu a obvodu kruhu približuje nižšie uvedený obrázok. Žlté štvorce majú obsah r^2. Oranžový štvorec sa skladá zo štyroch žltých štvorcov, takže má obsah 4\cdot r^2. Kruh má „o trochu menší“ obsah než oranžový štvorec, čo zodpovedá tomu, že obsah kruhu je približne 3{,}14 \cdot r^2. Obvod oranžového štvorca je 8\cdot r. Obvod kruhu je zase „o trochu menší“ – je to 2\pi \cdot r \approx 6{,}3 \cdot r.

Príklady
- Majme kruh s polomerom 3 cm. Jeho obvod je 2\pi \cdot 3 \approx 2 \cdot 3{,}14 \cdot 3 \approx 18{,}8 cm. Jeho obsah je \pi \cdot 3^2 \approx 3{,}14\cdot 9 \approx 28,3 cm².
- Kružnica s priemerom 2 cm má obvod \pi \cdot 2 \approx 6,3 cm. Jej vnútro má obsah \frac{1}{4} \pi \cdot 2^2 = \pi \approx 3,14 cm².
- Stredový kruh na futbalovom ihrisku má polomer 9{,}1 metru. Ak ho chceme obísť po jeho okrajovej čiare, prejdeme 2 \pi \cdot 9{,}1 \approx 57 metrov. Ak by sme chceli všetku trávu v kruhu nafarbiť na ružovo, museli by sme nafarbiť \pi \cdot 9{,}1^2 \approx 260 m² trávy.
Obsah kruhového výseku
Obsah kruhového výseku
Obsah kruhového výseku so stredovým uhlom \alpha a polomerom r vypočítame ako: \frac{\alpha}{360^{\circ}} \cdot \pi \cdot r^2
Dĺžka oblúka
Podobne, dĺžku oblúka, ktorý na kružnici s polomerom r a zodpovedá stredovému uhlu \alpha vypočítame ako: \frac{\alpha}{360^{\circ}} \cdot 2 \pi \cdot r
Príklady
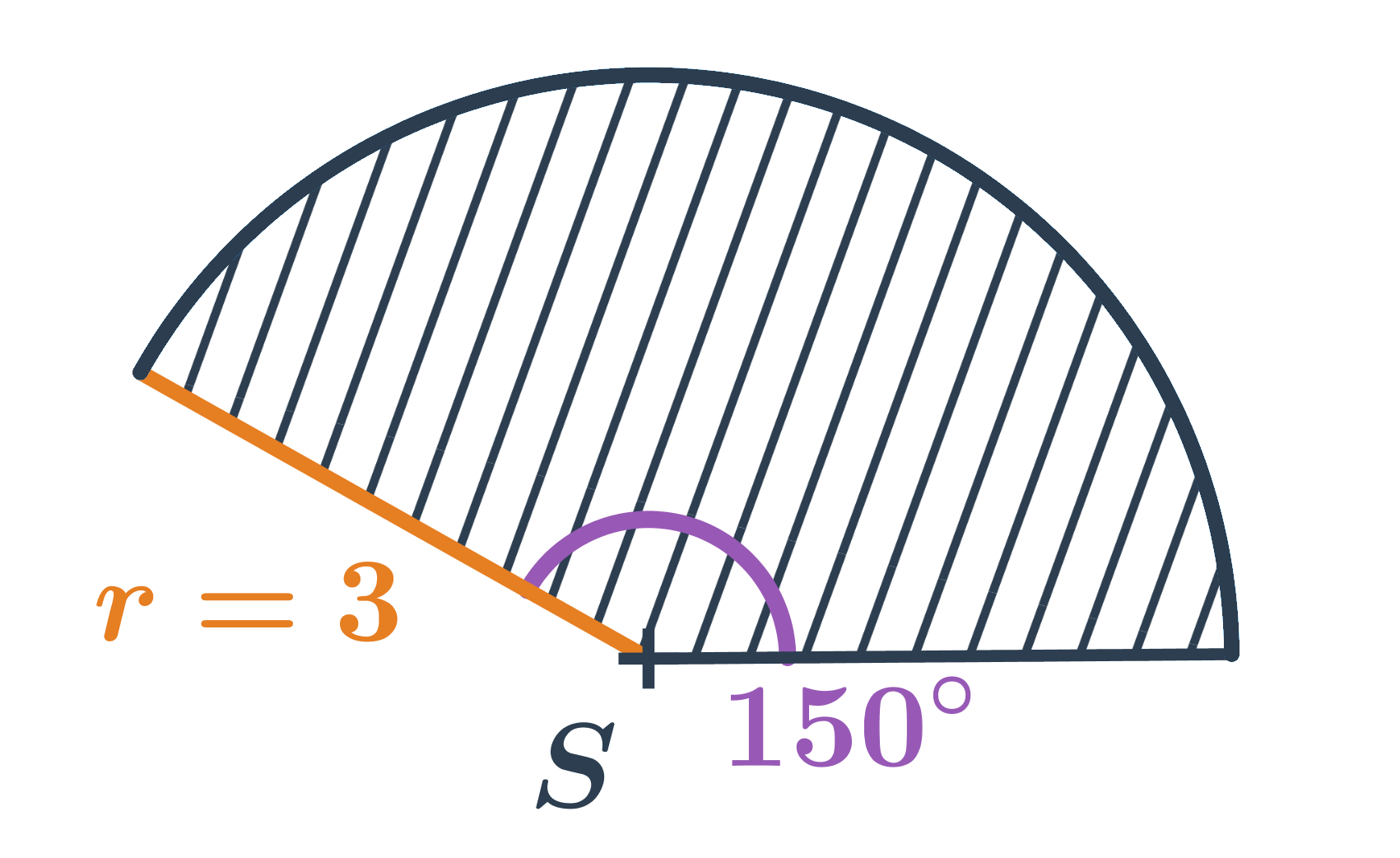
- Kruhový výsek na obrázku má obsah: \frac{150^{\circ}}{360^{\circ}} \cdot \pi \cdot 3^2 = \frac{5}{12} \cdot \pi \cdot 9 = \frac{15}{4} \pi
- Obsah celého kruhu (výseku so stredovým uhlom 360^{\circ}) je: \frac{360^{\circ}}{360^{\circ}} \cdot \pi \cdot r^2 = \pi \cdot r^2
- Dĺžka oblúka na obrázku je: \frac{90^{\circ}}{360^{\circ}} \cdot 2\pi \cdot 3 = \frac{1}{4} \cdot 6 \pi = \frac{3}{2}\pi
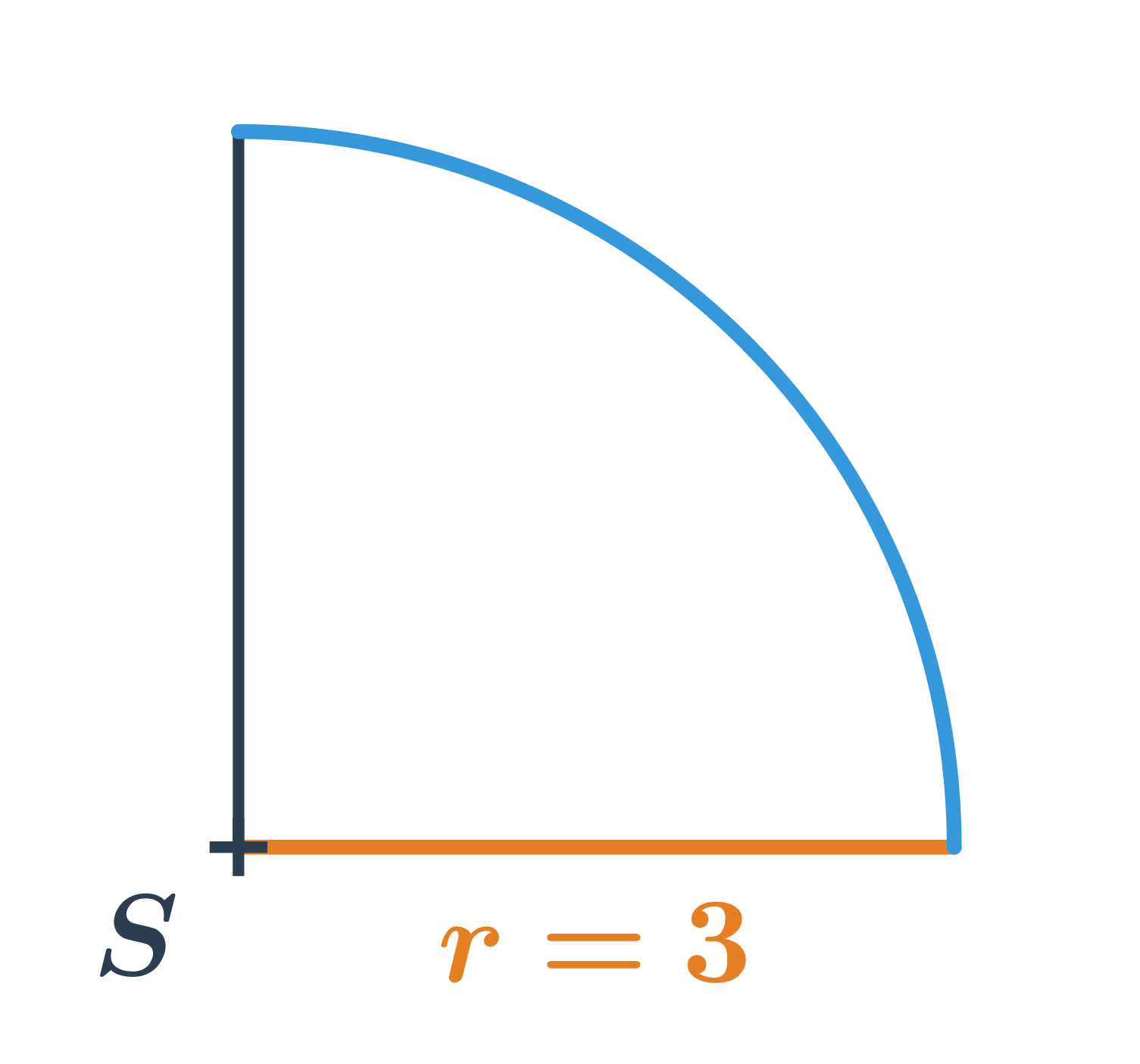
- Dĺžka celej kružnice (teda pre celých 360^{\circ}) je: \frac{360^{\circ}}{360^{\circ}} \cdot 2\pi \cdot r = 2\pi \cdot r
Obsah: mix
| Útvar | Vlastnosti | Obsah |
|---|---|---|
| trojuholník | strana a, príslušná výška v_a | S = \frac12 \cdot a\cdot v_a |
| štvorec | strana a | S = a^2 |
| obdĺžnik | strany a, b | S = a\cdot b |
| rovnobežník | strana a, príslušná výška v_a | S = a\cdot v_a |
| lichobežník | základne a, c, výška v | S = \frac12 \cdot (a+c) \cdot v |