Výpis prehľadov
Priamky
Prechádzate súhrny informácií k určitým témam. Systémy Vieme sa zameriavajú hlavne na ich precvičovanie. K cvičeniam k jednotlivým podtémam sa dostanete pomocou odkazov nižšie.
Podkapitoly
Priamka je jednoznačne určená bodom, ktorý na nej leží, a smerovým vektorom, čo si môžete prakticky vyskúšať v kapitolke Určenie priamky.
V rovine aj v priestore sa dá zapísať priamku ako množinu bodov, ktoré spĺňajú parametrickú rovnicu. V rovine dokážeme pre danú priamku napísať tiež všeobecnú rovnicu (ale v priestore nie).
Ak máme priamku popísanú rovnicou, dokážeme určiť vzájomnú polohu dvoch priamok alebo vzájomnú polohu priamky a bodu výpočtom.
HorePriamky: pojmy
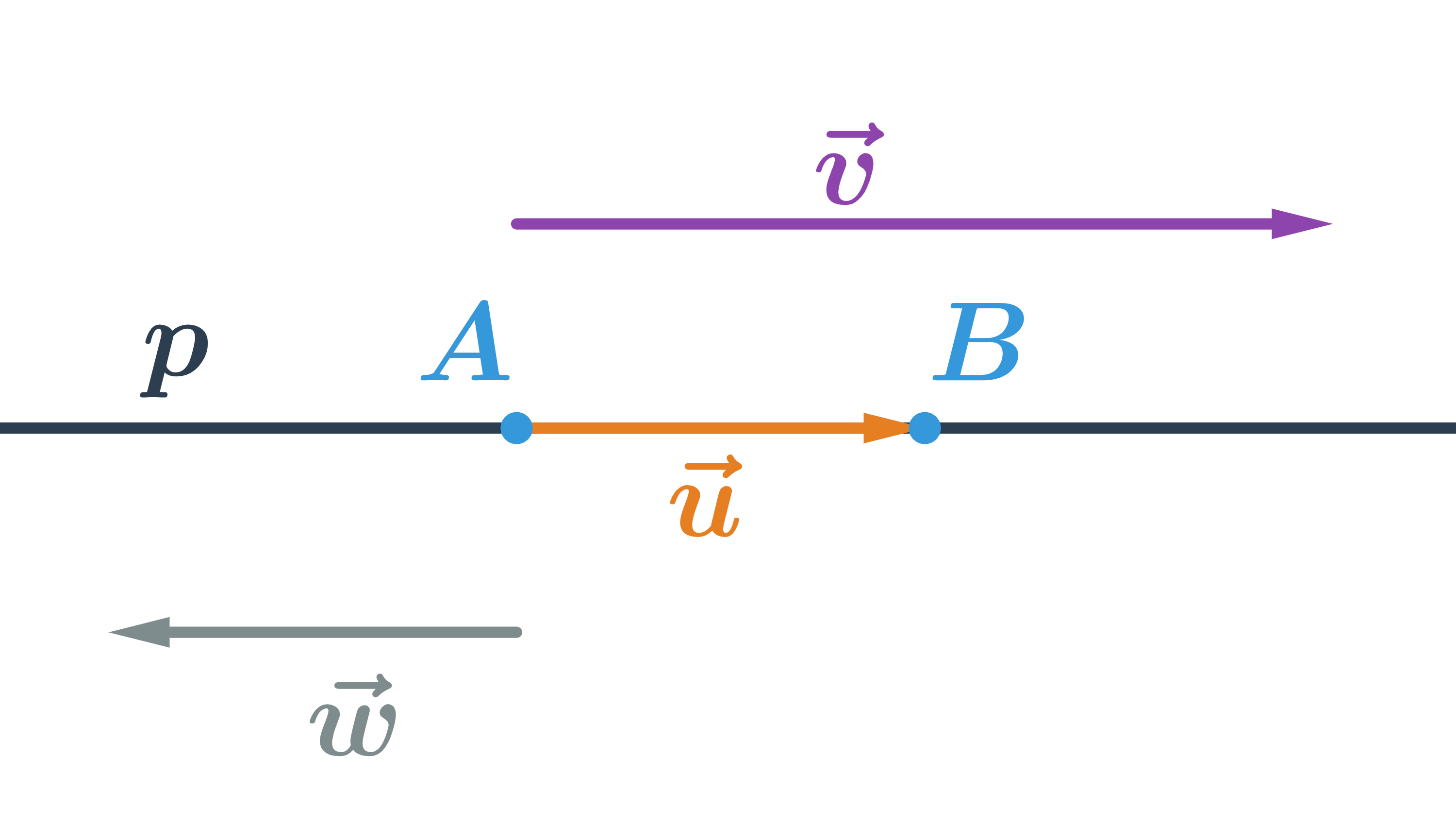
Priamka je jednoznačne určená dvomi bodmi, na obrázku je priamka p určená bodmi A a B. Každý vektor, ktorý je rovnobežný s vektorom \overrightarrow{AB} sa nazýva smerový vektor priamky p. Ktorýkoľvek z vektorov na obrázku je smerový vektor priamky p. K tomu, aby sme určili konkrétnu priamku ešte potrebujeme poznať jeden bod na priamke (priamka p na obrázku je určená bodom A a ktorýmkoľvek z vektorov \vec{u}, \vec{v}, \vec{w}).
Parametrické rovnice priamky
Priamka určená bodom A=[a_1;a_2] a vektorom \vec{u}=(u_1;u_2) má parametrické rovnice tvaru: \begin{array}{rrl}x&=&a_1+t\cdot u_1\\y&=&a_2+t\cdot u_2\\&&t\in\mathbb{R}\end{array} Skrátene môžeme vyjadriť p:X=A+t\vec{u}, číslo t nazývame parameter.
Ako súvisí hodnota parametra t s polohou bodu na priamke
- Priamka p je určená bodom A a vektorom \vec{u}=\overrightarrow{AB}, teda p:X=A+t\vec{u}
- Pre hodnotu t=0 dostaneme: X=A+t\vec{u}=A+0\cdot \vec{u} … bod A
- Pre hodnotu t=1 dostaneme: X=A+t\vec{u}=A+1\cdot \vec {u} … bod B
- Pre hodnotu t=2 dostaneme: X=A+t\vec{u}=A+2\cdot \vec {u} … bod C
- Pre hodnotu t=\frac{1}{2} dostaneme: X=A+t\vec{u}=A+\frac{1}{2}\cdot \vec{u} … bod D (stred úsečky AB)
- Pre hodnotu t=-1 dostaneme: X=A+t\vec{u}=A-1\cdot \vec{u} … bod E
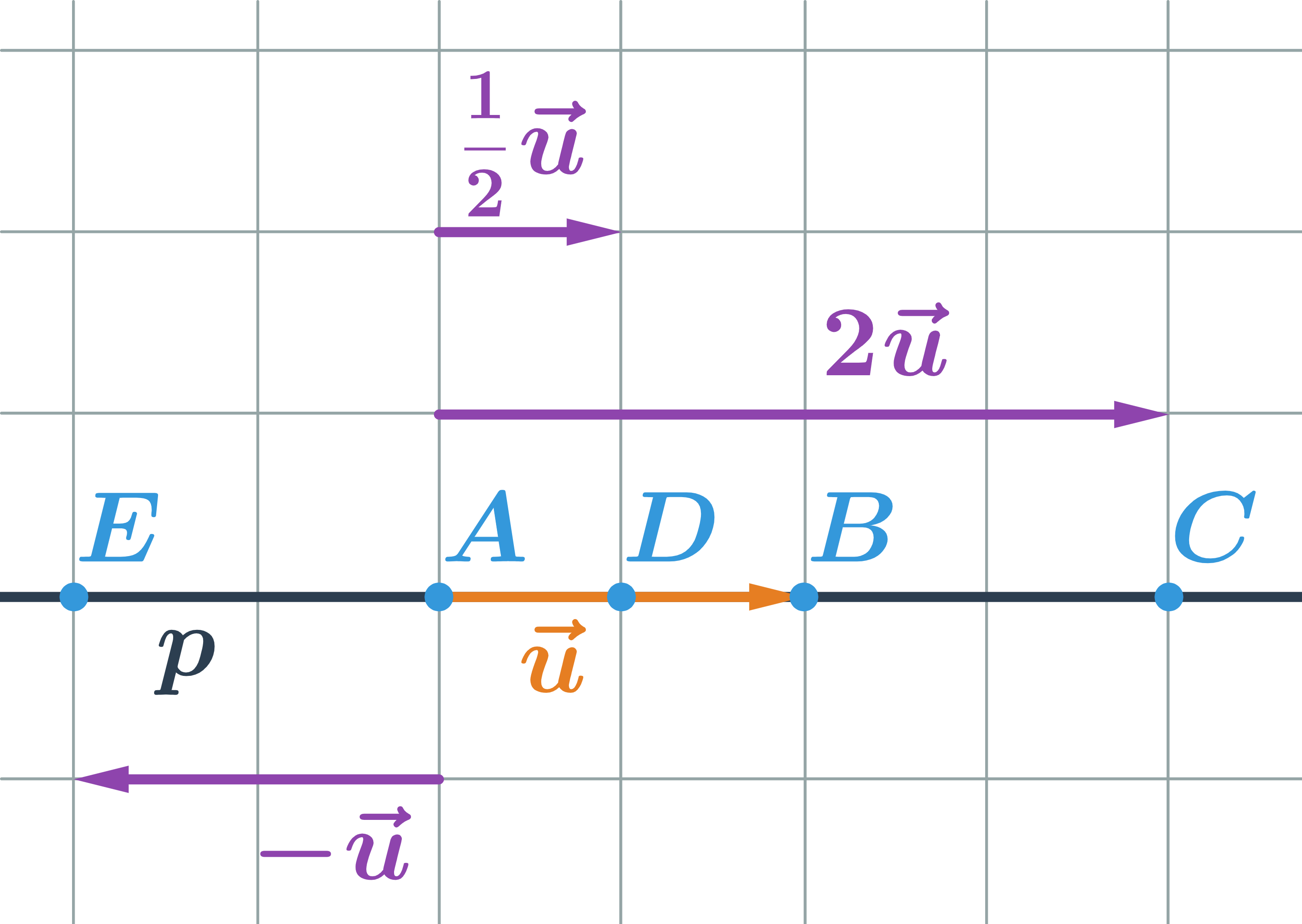
- Každá hodnota parametra určuje jeden bod na priamke, na určenie celej priamky teda potrebujeme všetky reálne čísla, preto píšeme t\in\mathbb{R}.
- Body, ktoré ležia na úsečke AB (teda body ležiace medzi bodmi A a B), vyjadríme parametricky, ak do rovnice X=A+t\vec{u} dosadíme hodnoty parametra t spĺňajúce 0\leq t\leq1.
Všeobecná rovnica priamky
Každý vektor kolmý k priamke p sa nazýva normálový vektor priamky p. Všeobecná rovnica priamky je rovnica v tvare: ax+by+c=0, kde konštanty a a b sú súradnice normálového vektora a c reálne číslo.
Súradnice smerového a normálového vektora priamky p
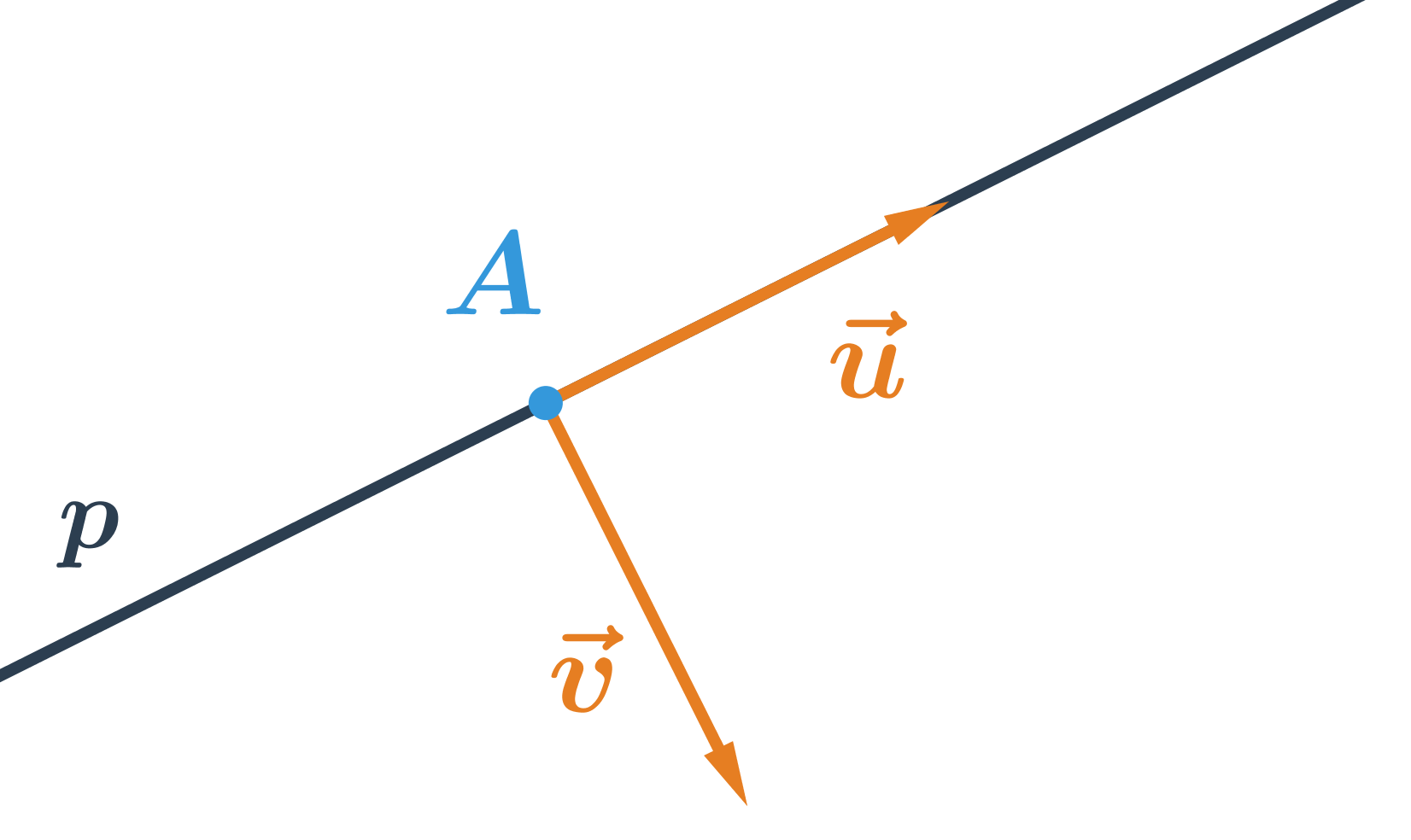
- Pre priamku danú všeobecnou rovnicou ax+by+c=0:
- \vec{v} je normálový vektor priamky p, jeho súradnice sú: \vec{v}=(a;b)
- \vec{u} je smerový vektor priamky p, pretože je to vektor kolmý na vektor \vec{v}=(a;b), jeho súradnice sú: \vec{u}=(-b;a)
- Pre priamku danú parametricky: \begin{array}{rrl}x&=&a_1+t\cdot u_1\\y&=&a_2+t\cdot u_2\\&&t\in\mathbb{R}\end{array}
- \vec{u} je smerový vektor priamky p, jeho súradnice sú: \vec{u}=(u_1;u_2)
- \vec{v} je normálový vektor priamky p, pretože je to vektor kolmý na vektor \vec{u}=(u_1;u_2), jeho súradnice sú: \vec{v}=(-u_2;u_1)
Všeobecná rovnica priamky rovnobežnej s osou x
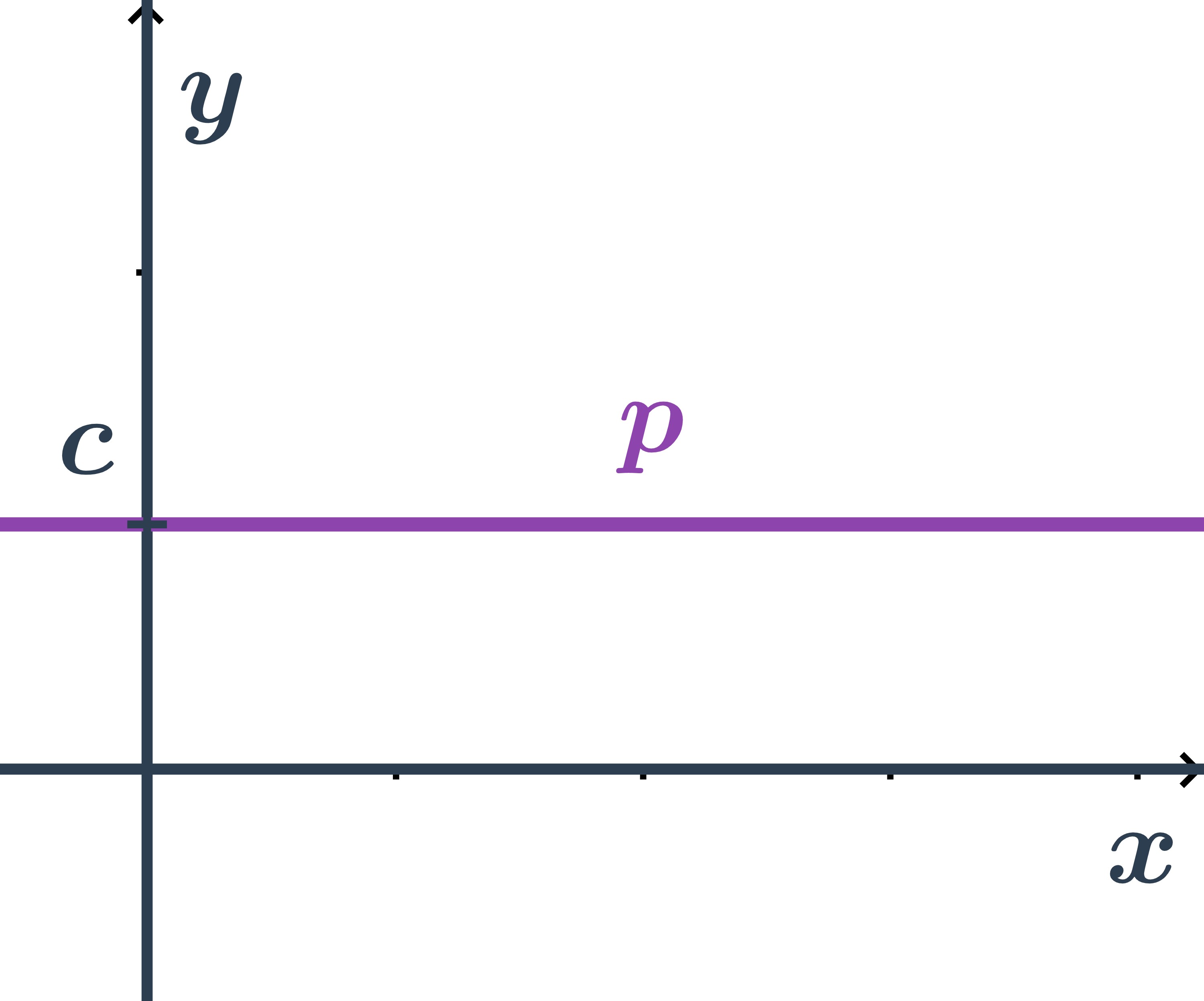
- Pre všetky body ležiace na priamke je druhá súradnica rovnaká a to: y=c
- Teda priamka má všeobecnú rovnicu: y-c=0
Všeobecná rovnica priamky rovnobežnej s osou y
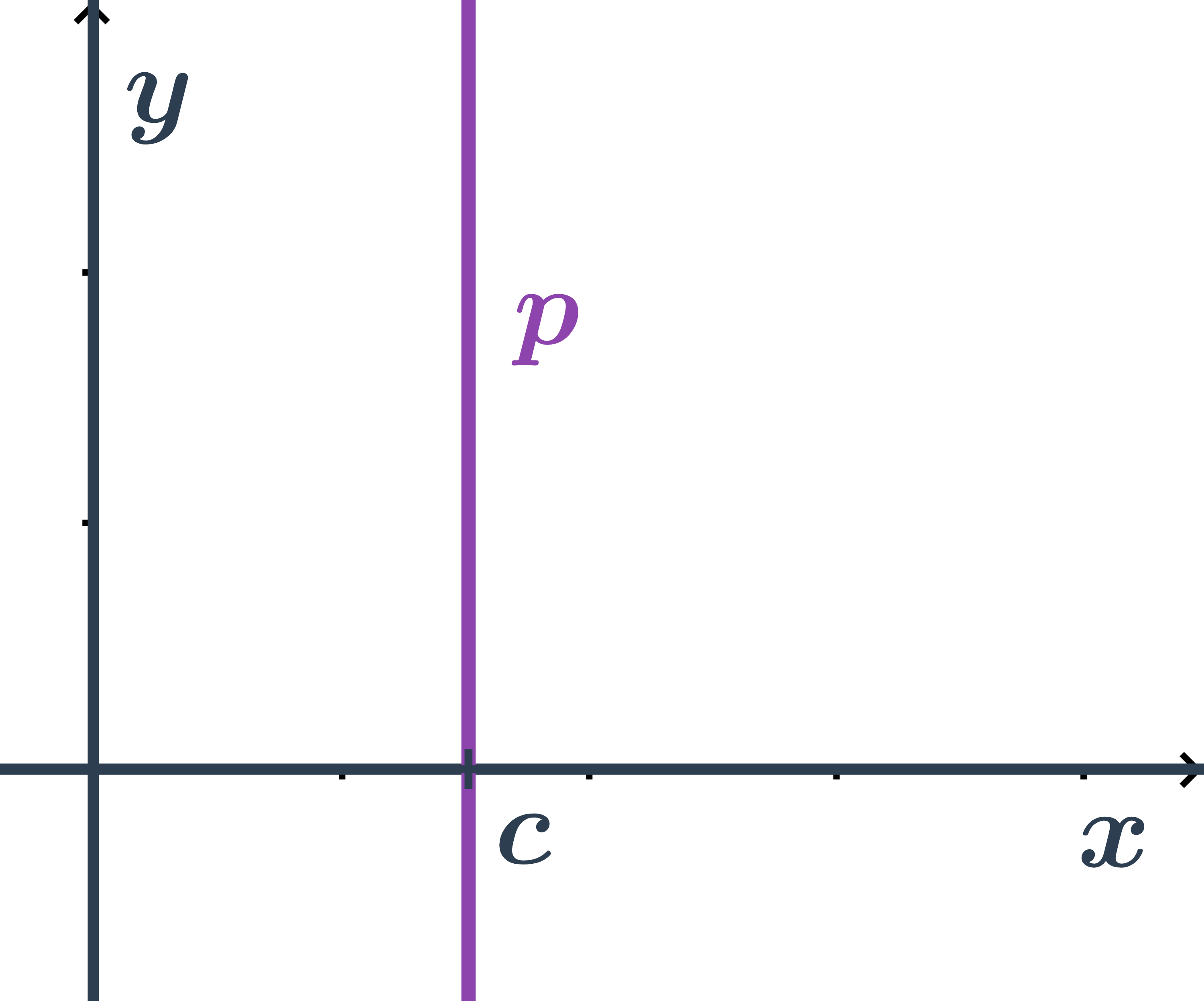
- Pre všetky body ležiace na priamke je prvá súradnica rovnaká a to: x=c
- Teda priamka má všeobecnú rovnicu: x-c=0
Bod a priamka
Bod M=[m_1;m_2] leží na priamke, ak jeho súradnice vyhovujú rovnici priamky. Ak je priamka daná všeobecnou rovnicou ax+by+c=0, pre súradnice bodu, ktorý leží na priamke platí: a\cdot m_1+b\cdot m_2+c=0. Ak je priamka daná parametricky, po dosiahnutí súradníc bodu vychádza z oboch rovníc rovnaká hodnota parametra t. (Viac o vzájomnej polohe bodu a priamky.)
Všeobecná rovnica priamky, ktorá prechádza počiatkom
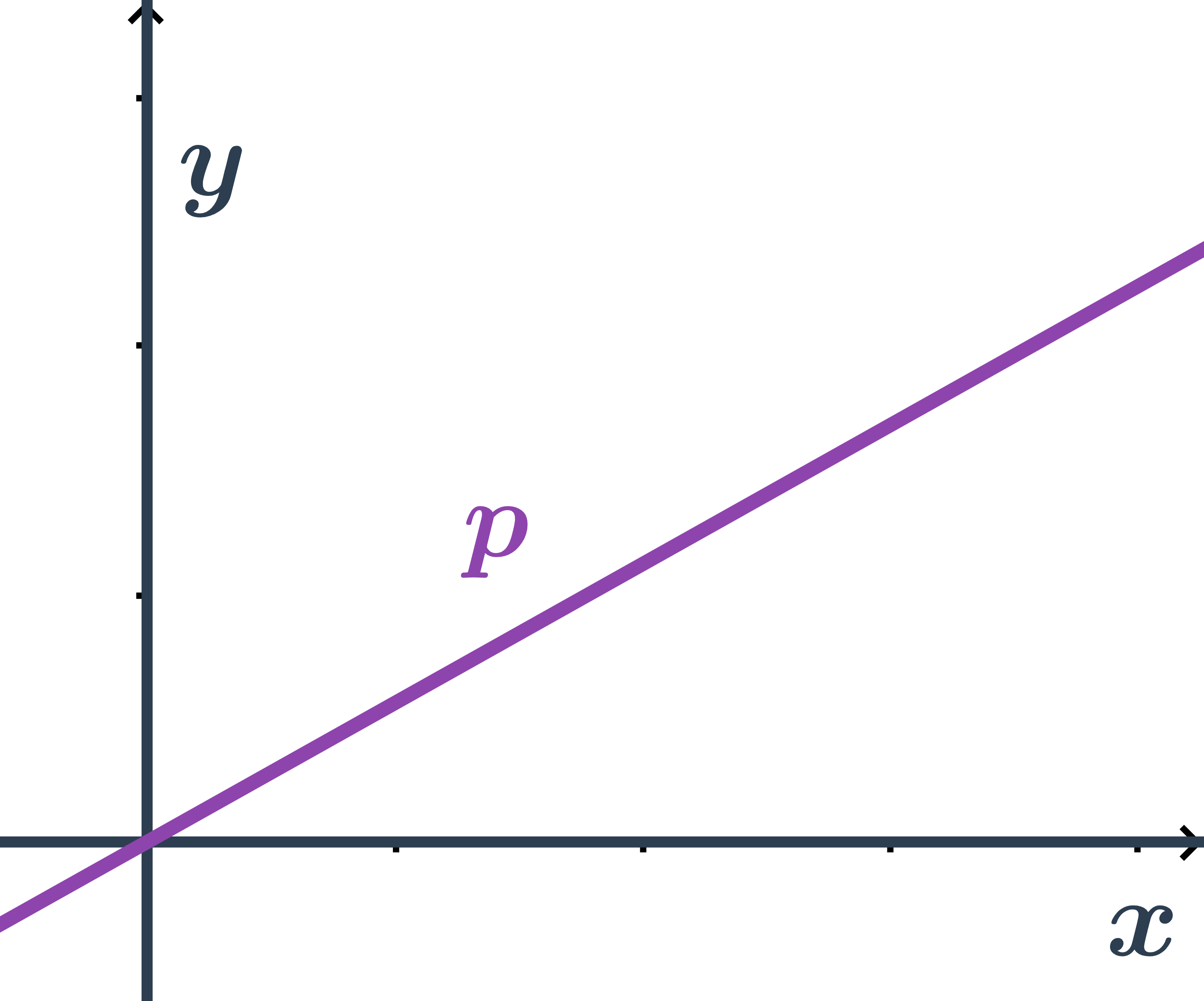
- Priamka prechádza bodom O=[0;0], teda súradnice počiatku spĺňajú jej všeobecnú rovnicu ax+by+c=0.
- Dosadíme súradnice bodu O a skúsime zistiť nejaké informácie o konštantách a,b,c.
- a\cdot0+b\cdot0+c=0\Leftrightarrow c=0
- Preto má priamka, ktorá prechádza počiatkom, všeobecnú rovnicu ax+by=0.
Dve priamky
Priamky rovnobežné majú rovnaký smer, teda ich smerové vektory sú kolineárne. Normálové vektory dvoch rovnobežných priamok sú tiež kolineárne. V špeciálnom prípade môžu byť priamky totožné.
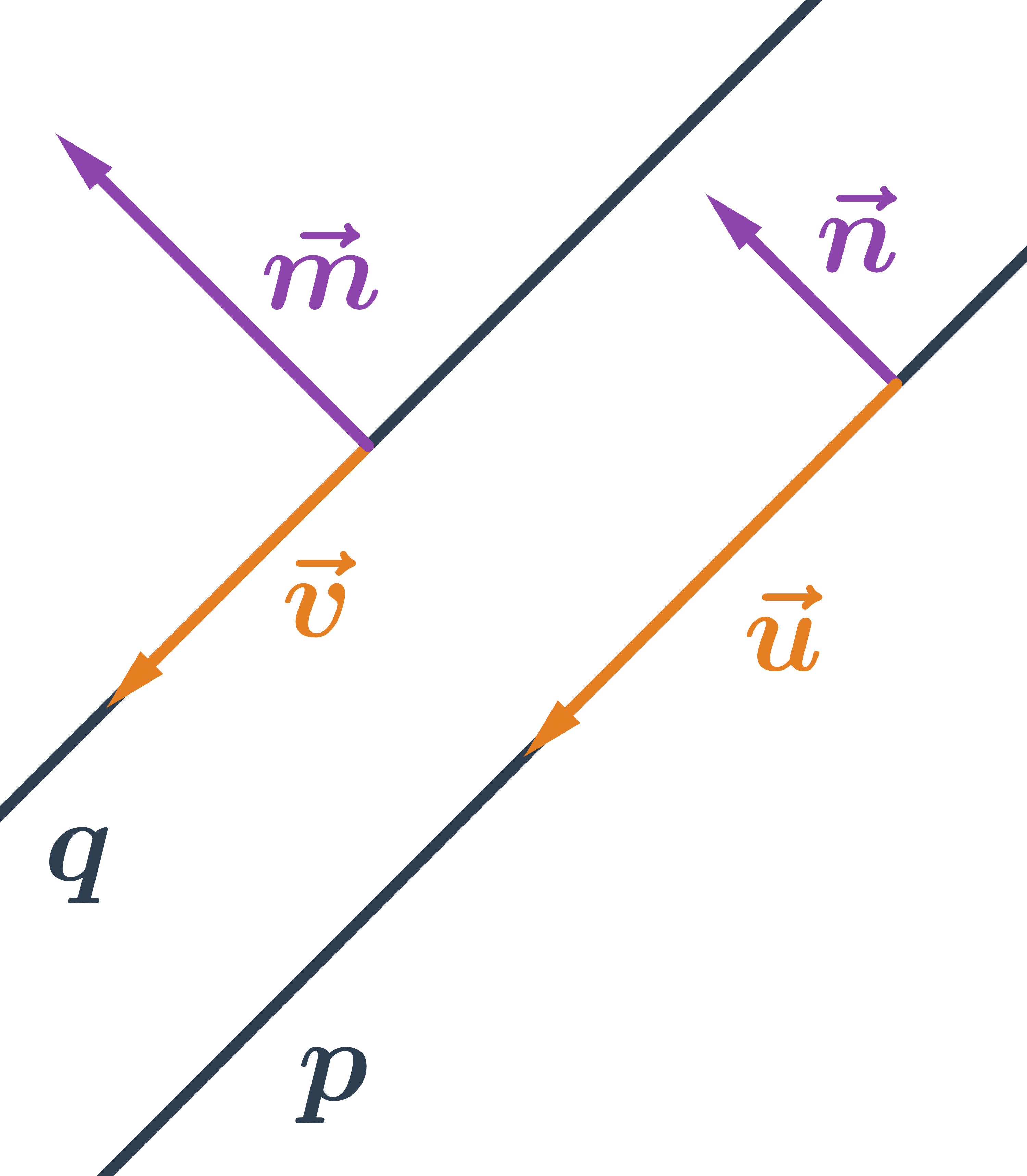
Priamky rôznobežné majú jeden spoločný bod, tento bod musí spĺňať rovnice oboch priamok. Ich smerové vektory nie sú kolineárne, normálové vektory tiež nie sú kolineárne.
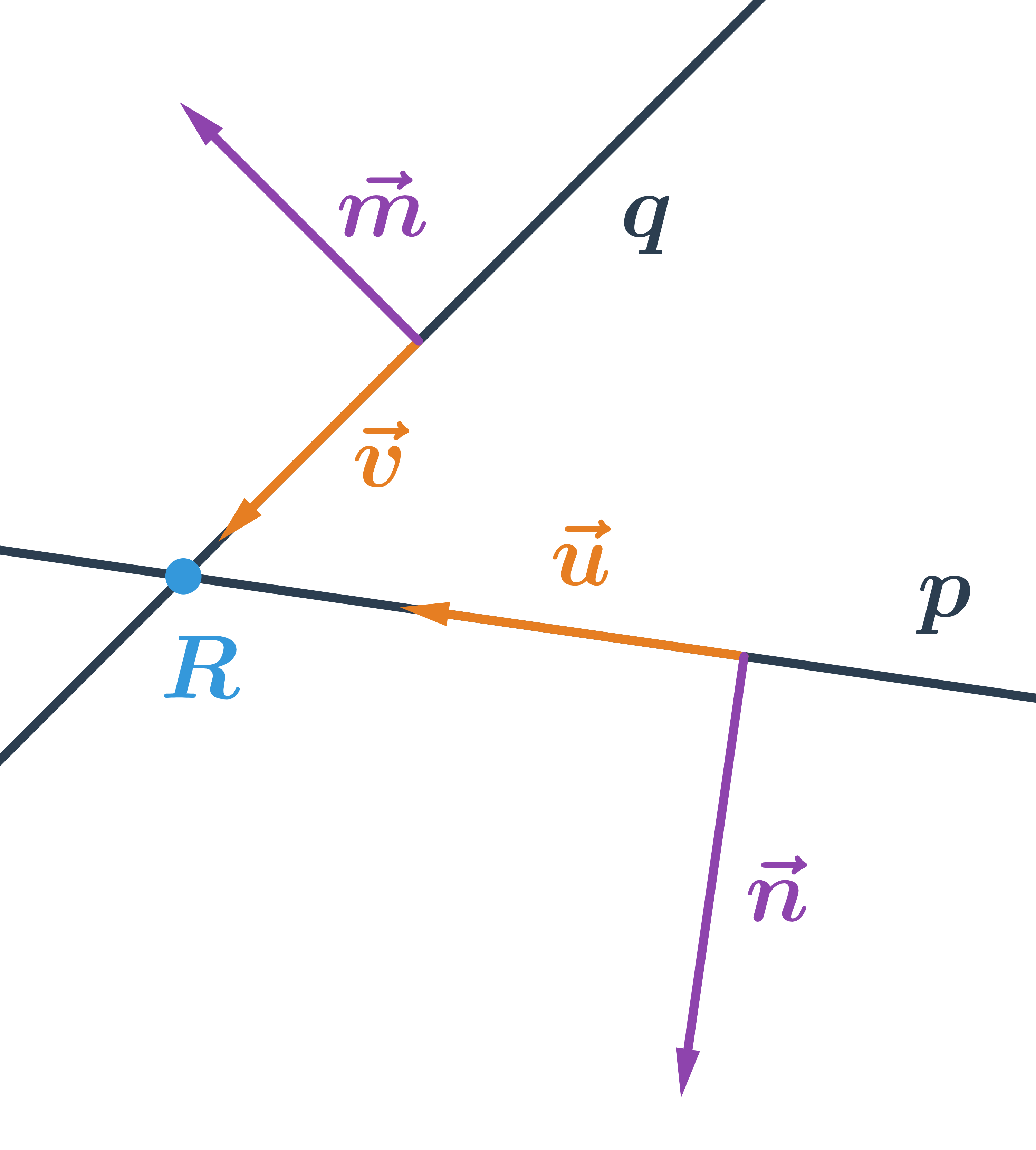
Viac o vzájomnej polohe dvoch priamok.
Priamka v priestore
Priamku v priestore nie je možné vyjadriť všeobecnou rovnicou. Parametrickú rovnicu priamky v priestore určíme podobne ako v rovine na základe znalosti súradníc smerového vektora a jedného bodu na priamke.
HoreUrčenie priamky
Priamka je väčšinou určená bodom a vektorom, prípadne dvomi bodmi.
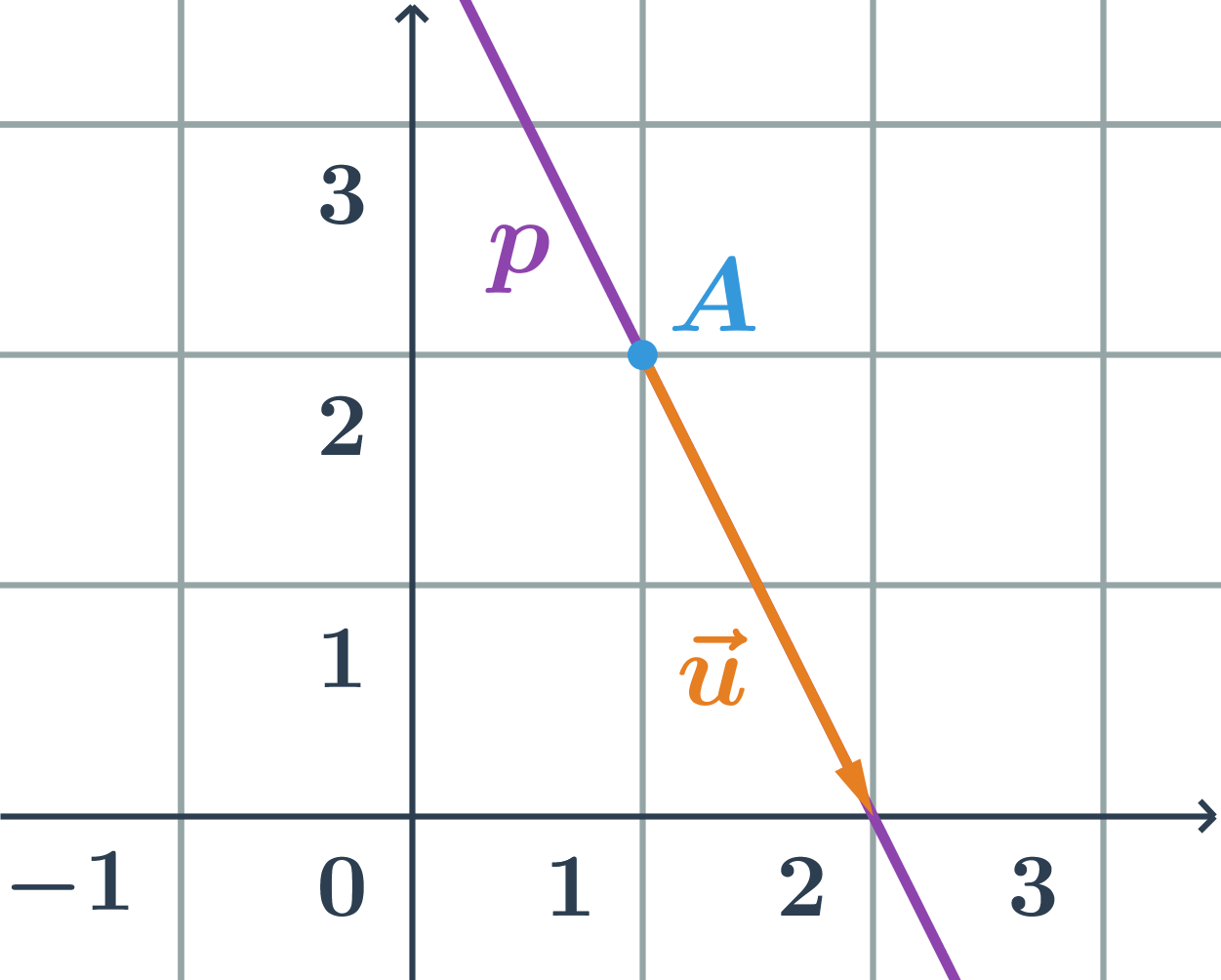
Priamka p na obrázku je určená napríklad:
- bodom A=[1;2], ktorý na nej leží a smerovým vektorom \vec{u}=(1;-2)
- alebo dvomi rôznymi bodmi [1;2] a [2;0], ktoré na nej ležia
Parametrické rovnice priamky v rovine
Priamka určená bodom A=[a_1;a_2] a smerovým vektorom \vec{u}=(u_1;u_2) má parametrické rovnice tvaru:
\begin{array}{rrl}x&=&a_1+t\cdot u_1\\y&=&a_2+t\cdot u_2\\&&t\in\mathbb{R}\end{array}
Skrátene môžeme vyjadriť p:X=A+t\vec{u}, číslo t nazývame parameter. Ak poznáme dva body A, B ležiace na priamke, smerový vektor je napríklad \vec{u}=\overrightarrow{AB}.
Parametrické rovnice priamky p určenej bodmi A=[1;2] a B=[3;1]
- priamka p je určená bodom A a smerovým vektorom \vec{u}=\overrightarrow{AB}=B-A=(2;-1)
- parametrické rovnice priamky p: \begin{array}{rrl}x&=&1+2t\\y&=&2-t\\&&t\in\mathbb{R}\end{array}
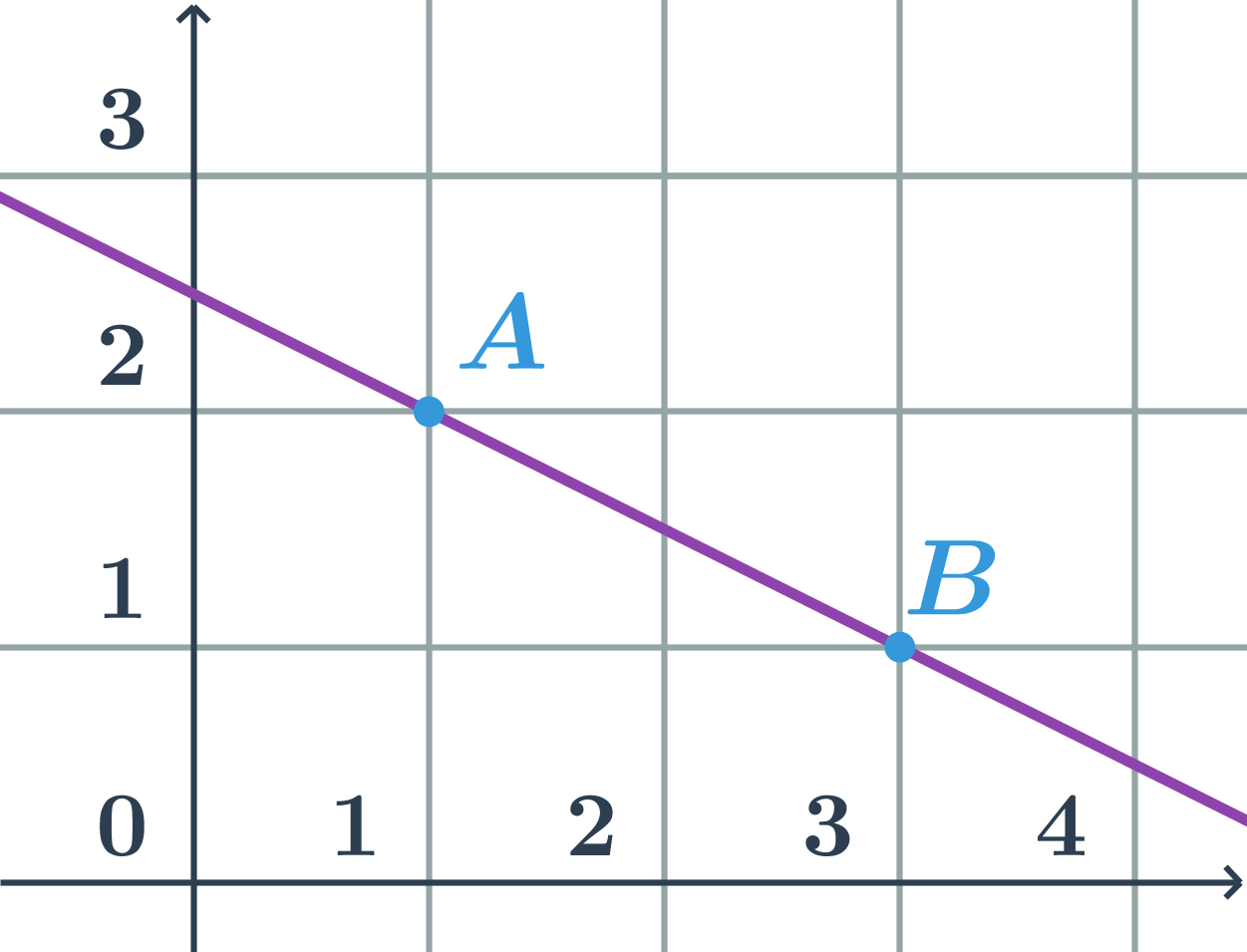
Rôzne parametrické rovnice priamky na obrázku
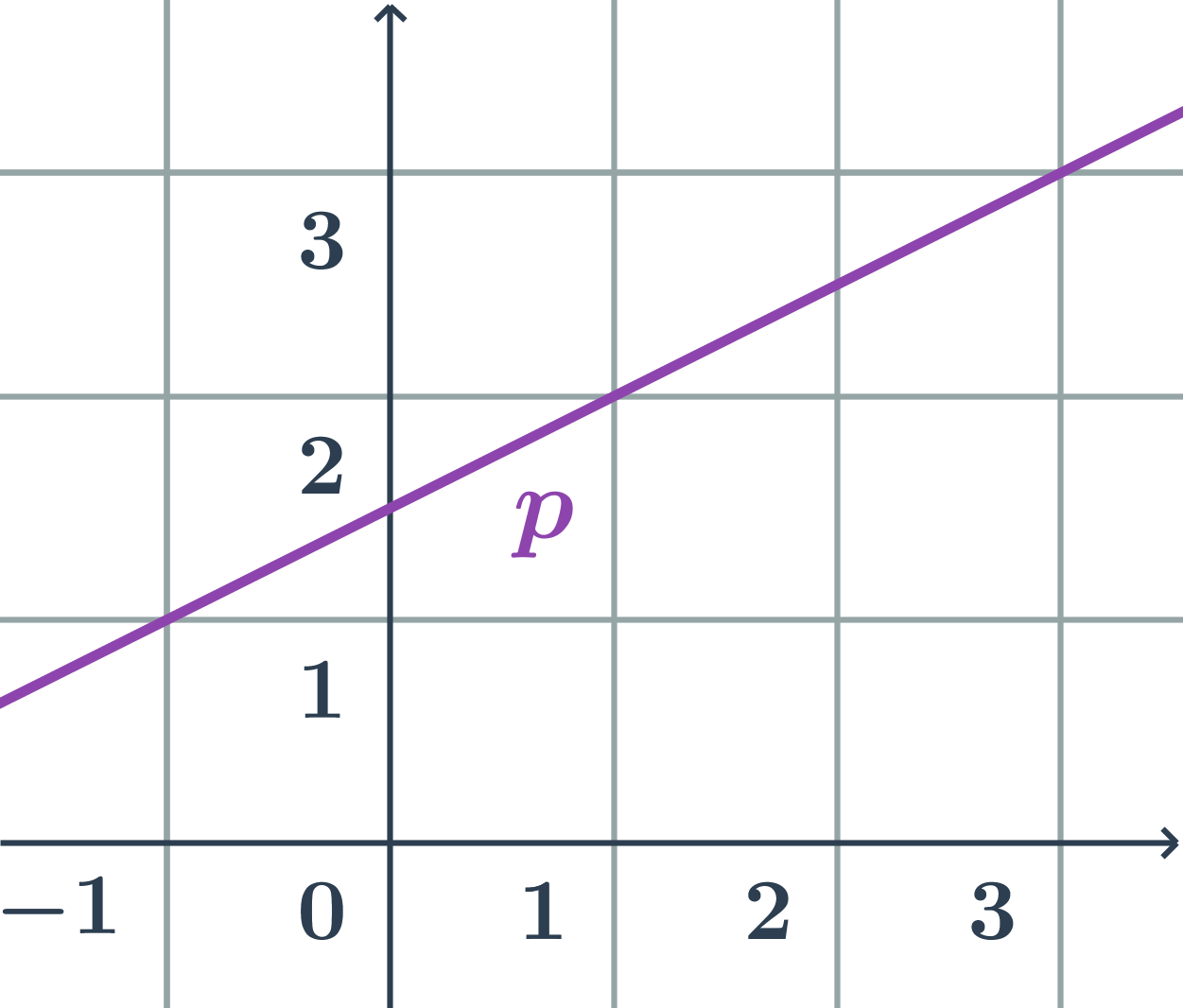
Určíme súradnice smerového vektora a jedného bodu na priamke:
- napríklad: \vec{u}=(2;1), A=[1;2]
- parametrické rovnice priamky p: \begin{array}{rrl}x&=&1+2t\\y&=&2+t\\&&t\in\mathbb{R}\end{array}
Ďalšia možnosť parametrického vyjadrenia:
- \vec{v}=(-4;-2), B=[3;3]
- parametrické rovnice priamky p: \begin{array}{rrl}x&=&3-4t\\y&=&3-2t\\&&t\in\mathbb{R}\end{array}
Na určenie parametrických rovníc môžeme vybrať ktorýkoľvek bod ležiaci na priamke a akýkoľvek zápis súradníc smerového vektora, možností ako parametricky vyjadriť danú priamku je teda nekonečne veľa.
Všeobecná rovnica priamky v rovine
Všeobecná rovnica priamky v rovine má tvar: ax+by+c=0, kde konštanty a a b sú súradnice normálového vektora a c reálne číslo. Normálový vektor \vec{n}=(a;b) je vektor kolmý na danú priamku, teda aj kolmý na smerový vektor priamky.
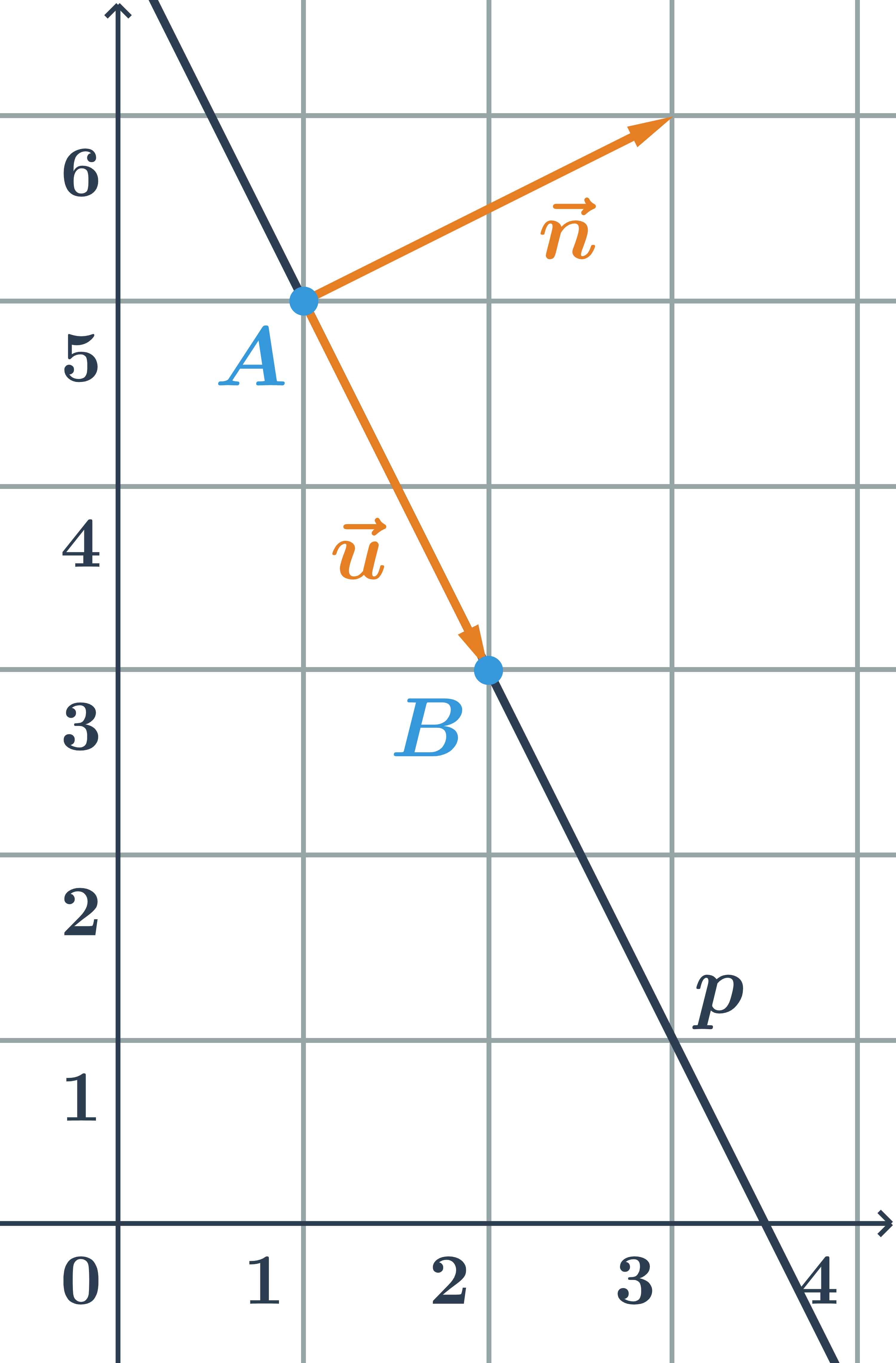
Všeobecná rovnica priamky p určené body A=[1;5] a B=[2;3]
- Priamka p je určená bodom A a smerovým vektorom \vec{u}=\overrightarrow{AB}=B-A=(1;-2).
- Normálový vektor je kolmý na vektor \vec{u}=(1;-2), teda napríklad vektor \vec{n}=(2;1).
- Súradnice normálového vektoru sú konštanty a a b vo všeobecnej rovnici priamky. Všeobecná rovnica má tvar: 2x+y+c=0
- Konštantu c dopočítame dosadením súradníc bodu A=[1;5] :
- 2\cdot1+5+c=0\Rightarrow c=-7
- Všeobecná rovnica priamky p je: 2x+y-7=0
Všeobecná rovnica priamky danej parametricky
Určite všeobecnú rovnicu priamky p, ktorá je daná nasledujúcou parametrickou sústavou rovníc: \begin{array}{rrl}x&=&1+2t\\y&=&4+6t\\&&t\in\mathbb{R}\end{array}
- Priamka p je určená bodom A=[1;4] a smerovým vektorom \vec{u}=(2;6).
- Súradnice smerového vektora môžeme upraviť na tvar: \vec{u}=(1;3).
- Normálový vektor je kolmý na vektor \vec{u}=(1;3), teda napríklad vektor \vec{n}=(3;-1).
- Súradnice normálového vektora sú konštanty a a b vo všeobecnej rovnici priamky. Všeobecná rovnica má tvar: 3x-y+c=0
- Konštantu c dopočítame dosadením súradníc bodu A=[1;4] :
- 3\cdot1-4+c=0\Rightarrow c=1
- Všeobecná rovnica priamky p je: 3x-y+1=0
Parametrické vyjadrenie priamky danej všeobecnou rovnicou
Určite parametrické vyjadrenie priamky p, ktorá má všeobecnú rovnicu: 3x-2y+4=0.
- Priamka p má normálový vektor \vec{n}=(3;-2).
- Smerový vektor je kolmý na vektor \vec{n}=(3;-2), teda napríklad vektor \vec{u}=(2;3).
- Určíme jeden bod na priamke p : jednu súradnicu môžeme zvoliť, napríklad x=0, druhú súradnicu dopočítame: 3\cdot0-2y+4=0\Rightarrow y=2
- Zo všeobecnej rovnice sme teda zistili, že na priamke leží bod A=[0;2].
- Parametrické vyjadrenie priamky p je: \begin{array}{rrl}x&=&0+3t\\y&=&2-2t\\&&t\in\mathbb{R}\end{array}
Smernicový tvar rovnice priamky
Každú priamku p, ktorá nie je rovnobežná s osou y môžeme vyjadriť v tvare: y=kx+q, kde k,q\in\mathbb{R}.
Tento tvar sa nazýva smernicový tvar rovnice priamky.
Konštanta k sa nazýva smernica a jej hodnota je tangens uhla, ktorý zviera priamka p s kladnou časťou osi x, teda: k=\tan \varphi.
Konštanta q určuje priesečník priamky p s osou y, súradnice priesečníka sú: P=[0;q]. Pre priamku, ktorá prechádza počiatkom je q=0, teda smernicový tvar jej rovnice je: y=kx.
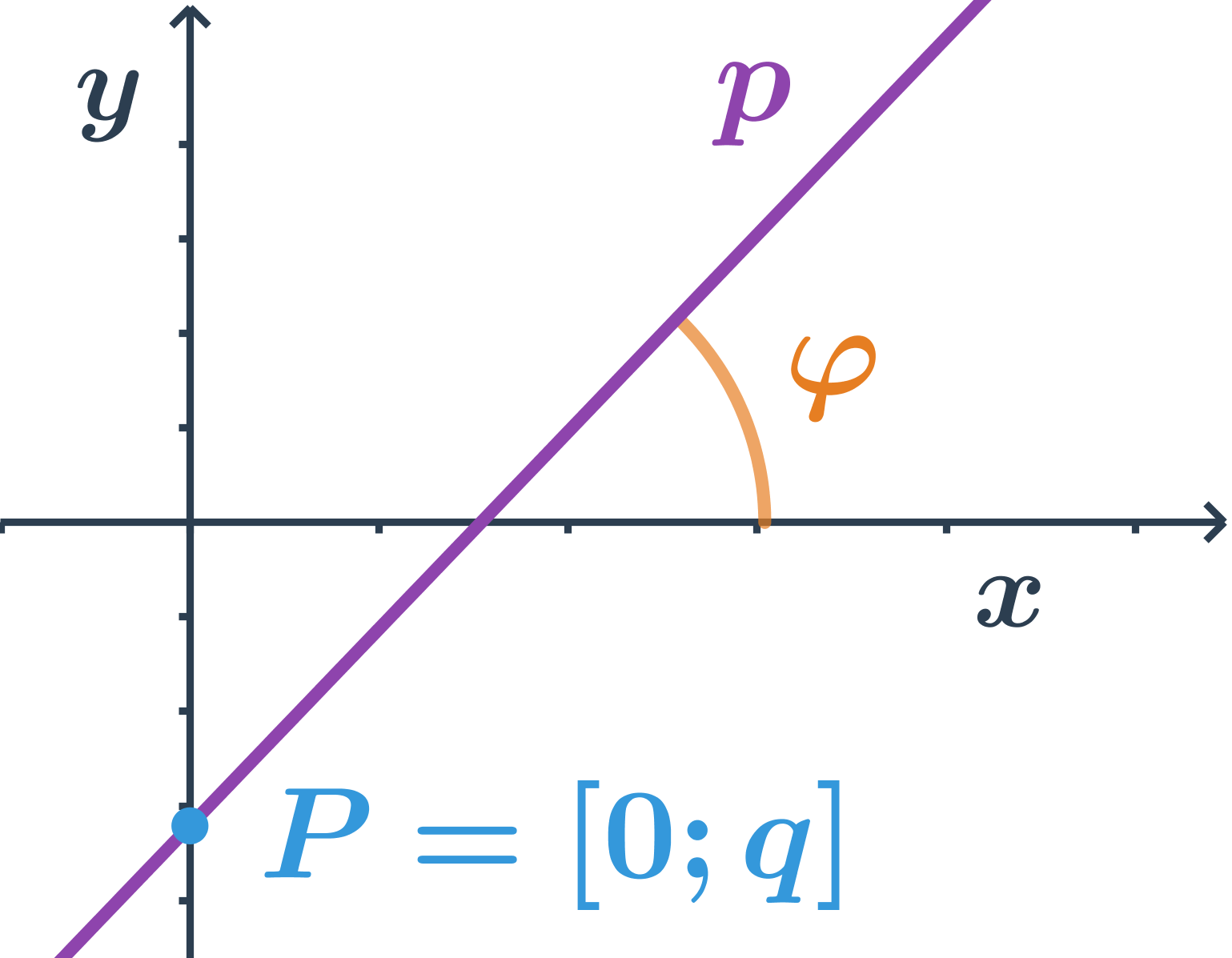
Smernica priamky, ktorá má smerový vektor \vec{u}=(u_1;u_2) je podiel súradnic smerového vektora:
k=\tan \varphi=\frac{u_2}{u_1}
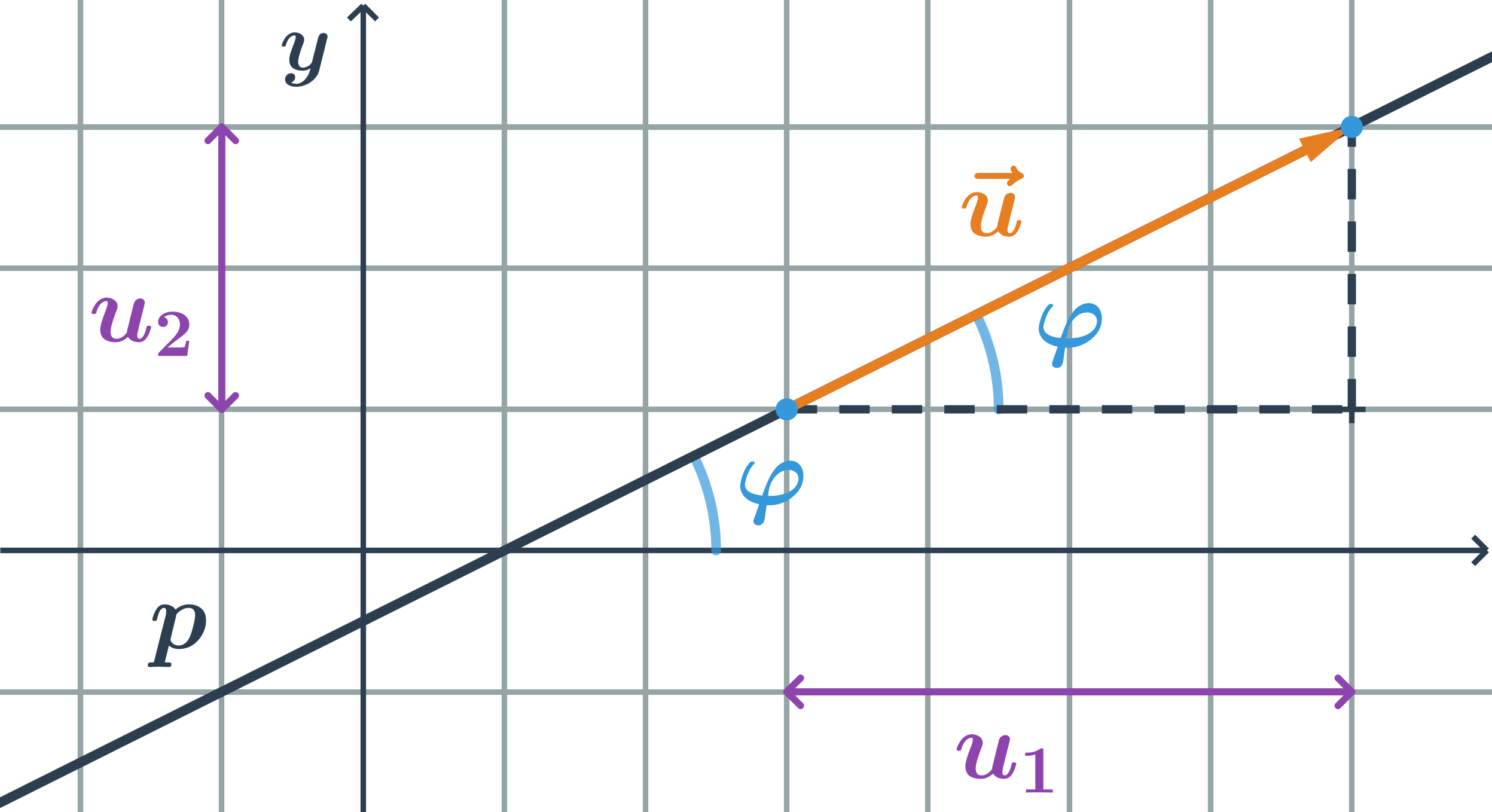
Rôzne hodnoty smernice
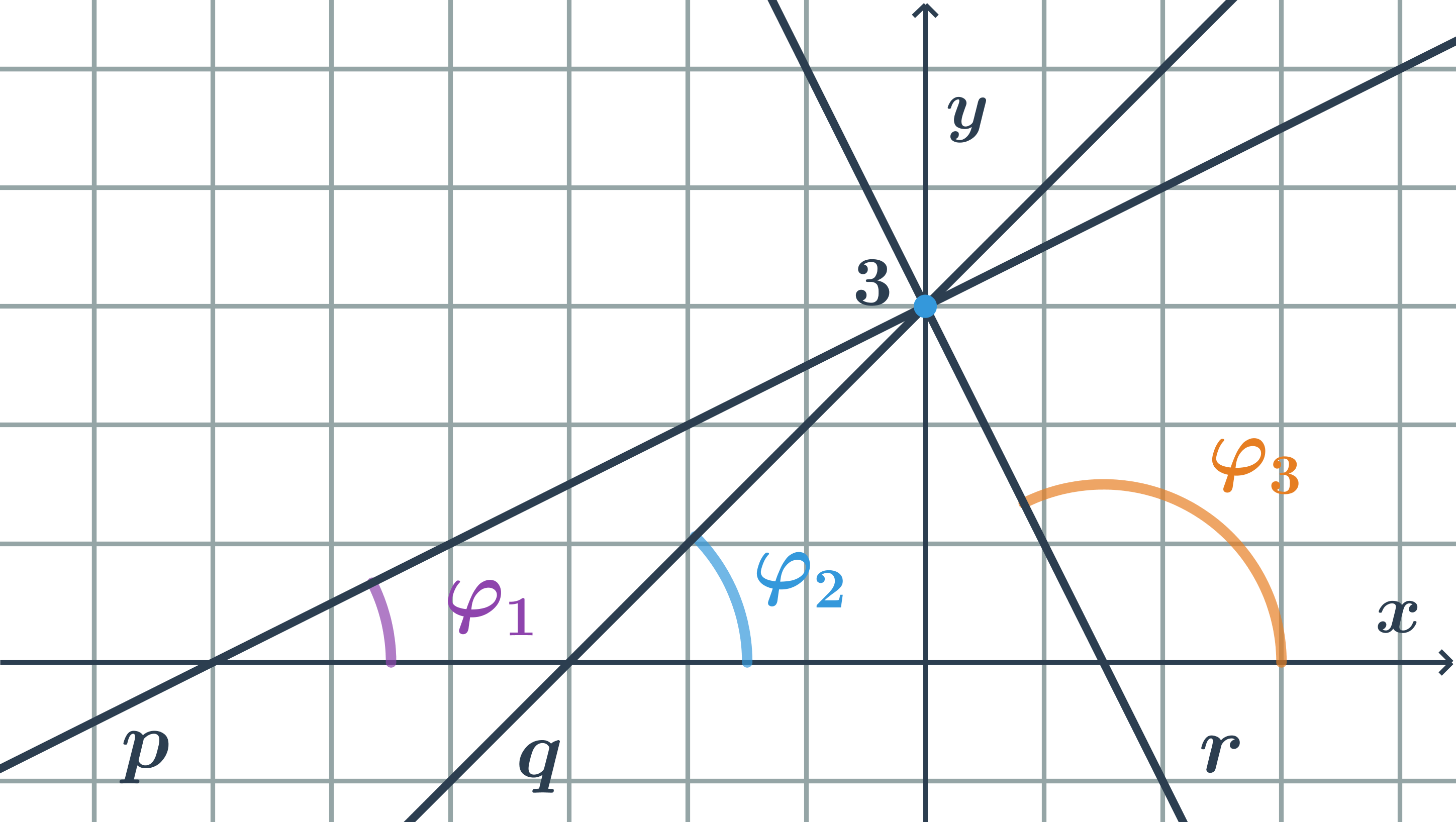
- Smernica priamky p: k_1=\tan \varphi_1=\frac{1}{2}
- Smernica priamky q: k_2=\tan \varphi_2=\frac{1}{1}=1
- Smernica priamky r: k_3=\tan \varphi_3=\frac{2}{1}=2
- Čím väčšia odchýlka od kladnej časti osi x, tým väčšia hodnota smernice k.
- Priamka rovnobežná s osou x zviera s kladnou časťou osi x uhol 0^\circ a teda jej smernica je \tan 0^\circ=0.
- Priamka rovnobežná s osou y zviera s kladnou časťou osi x uhol 90^\circ a pre túto hodnotu funkcie tangens nie je definovaná, preto nemôžeme určiť smernicu.
Smernicový tvar priamky z obrázka
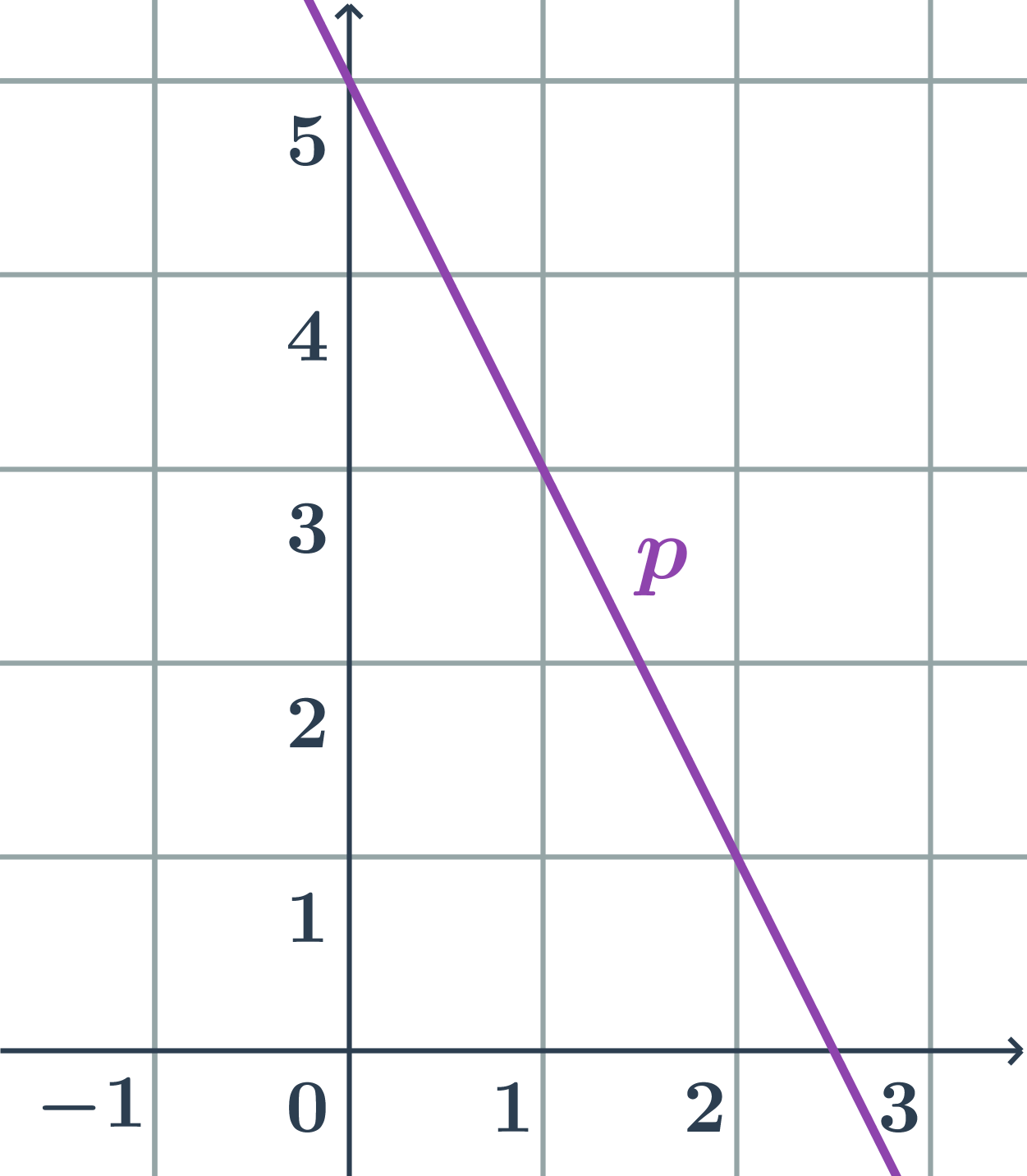
Hľadáme smernicový tvar rovnice priamky: y=kx+q.
- Pre nájdenie konštánt k a q určíme smerový vektor priamky p a priesečník s osou y.
- smerový vektor priamky: \vec{u}=(1;-2)
- smernica: k=\tan \varphi=\frac{u_2}{u_1}=\frac{-2}{1}=-2
- priesečník priamky s osou y: P=[0;5]
- konštanta q=y_P=5
- priamka na obrázku má smernicový tvar y=-2x+5
Dve priamky
Dve rovnobežné priamky zvierajú s kladnou časťou osi x rovnaký uhol, majú teda rovnakú smernicu.
Pre dve na seba kolmé priamky platí:
- priamka p má smerový vektor \vec{u}=(u_1;u_2) a teda smernicu: k=\frac{u_2}{u_1}
- každá priamka na ňu kolmá má smerový vektor (-u_2;u_1) a teda smernicu: \frac{-u_2}{u_1}=-\frac{1}{k}
Vzájomná poloha priamok v rovine
Vzájomnú polohu dvoch priamok môžeme ľahko určiť, ak poznáme súradnice ich smerových, prípadne normálových vektorov. Rovnobežne priamky majú rovnaký smer, teda ich smerové vektory sú kolineárne. Normálové vektory dvoch rovnobežných priamok sú tiež kolineárne. V špeciálnom prípade môžu byť priamky totožné. Rôznobežné priamky majú jeden spoločný bod, tento bod musí spĺňať rovnice oboch priamok. Ich smerové vektory nie sú kolineárne, normálové vektory tiež nie sú kolineárne.
Rovnobežky zadané parametrickými rovnicami
Určite vzájomnú polohu dvoch priamok p, q zadaných parametricky:
p: \begin{array}{rrl}x&=&-3+3t\\y&=&\hspace{0.25cm}2+t\\&&\hspace{0.25cm}t\in\mathbb{R}\end{array} \hspace{0.5cm}q: \begin{array}{rrl}x&=&1-3s\\y&=&2-s\\&&s\in\mathbb{R}\end{array}
- smerový vektor priamky p:\hspace{0.25cm}\vec{u}=(3;1)
- smerový vektor priamky q:\hspace{0.25cm}\vec{v}=(-3;-1)
- Priamky p a q sú rovnobežné, pretože ich smerové vektory sú kolineárne.
- Overíme, že priamky nie sú totožné. Stačí určiť, či bod, ktorý leží na jednej priamke neleží na priamke druhej.
- Na priamke p leží napríklad bod A=[-3;2].
- Overíme, že tento bod neleží na priamke q dosadením súradníc bodu A do rovníc priamky q: \begin{array}{rrl}-3&=&1-3s \Rightarrow s=\frac{4}{3}\\2&=&2-\hspace{0.15cm}s\Rightarrow s=0\end{array}
- Vyšli rôzne hodnoty parametra s, takže bod A neleží na q \Rightarrow priamky nie sú totožné
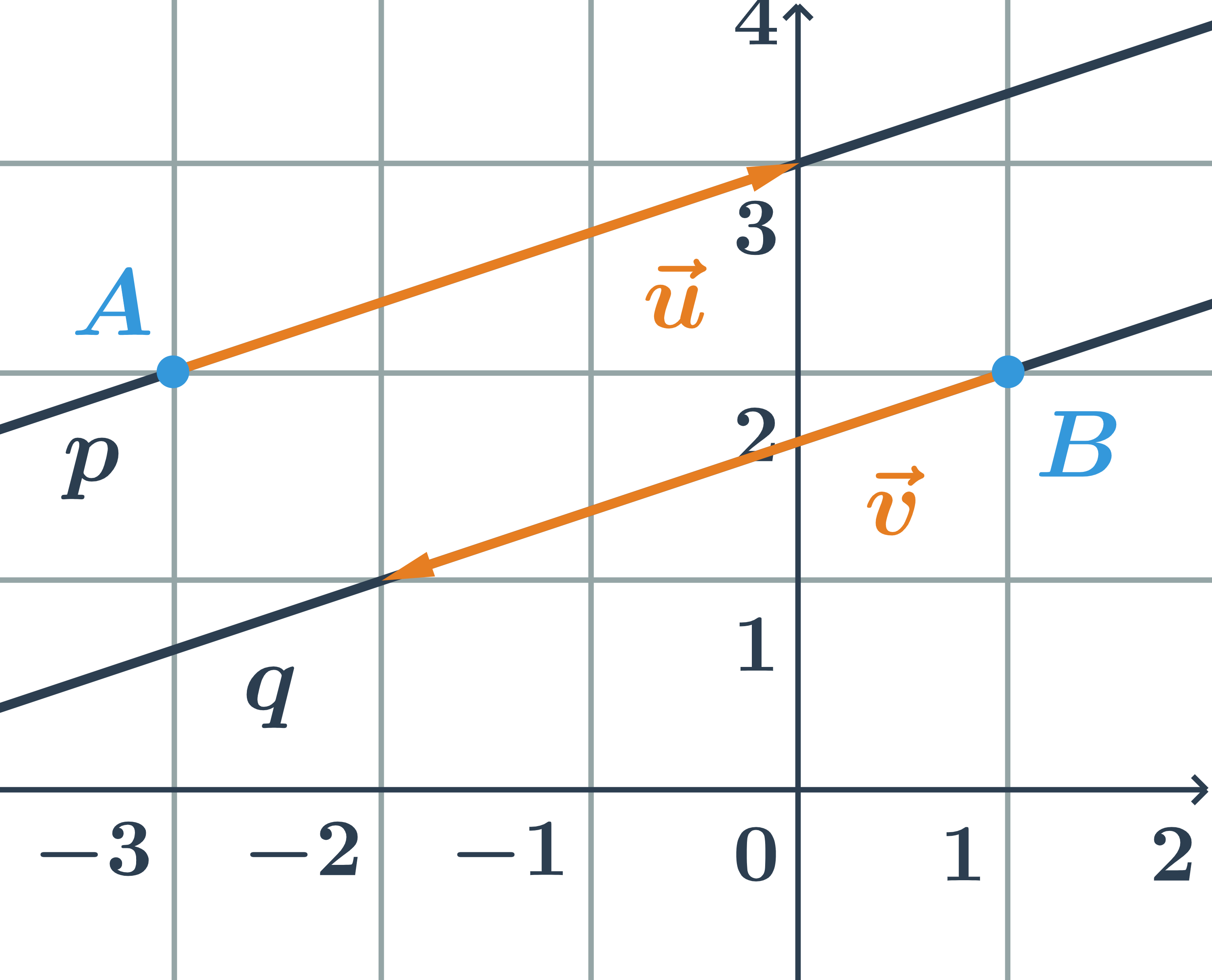
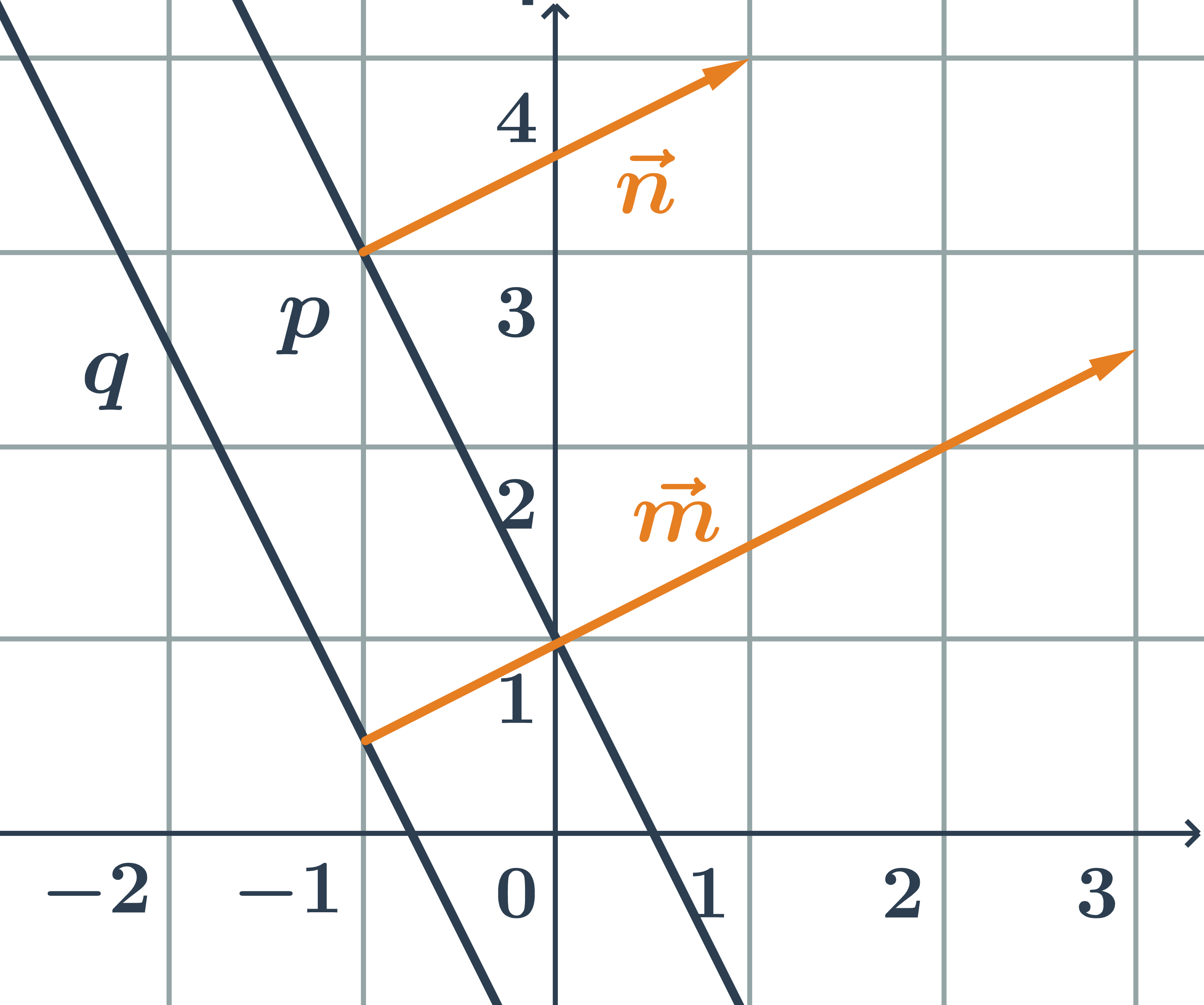
Rovnobežky zadané všeobecnými rovnicami
Určite vzájomnú polohu dvoch priamok daných všeobecnými rovnicami p: 2x+y-1=0 a q:4x+2y+3=0.
- normálový vektor priamky p:\hspace{0.25cm}\vec{n}=(2;1)
- normálový vektor priamky q:\hspace{0.25cm}\vec{m}=(4;2)
- Priamky p a q sú rovnobežné, pretože ich normálové vektory sú kolineárne.
- Overíme, že priamky nie sú totožné. Stačí určiť, či bod, ktorý leží na jednej priamke neleží na priamke druhej.
- Na priamke p leží napríklad bod A=[0;1].
- Overíme, či A leží na p dosadením súradníc bodu A do rovnice priamky p: 4\cdot0+2\cdot1+3\neq 0
- A nespĺňa rovnicu, takže neleží na priamke q \Rightarrow priamky nie sú totožné
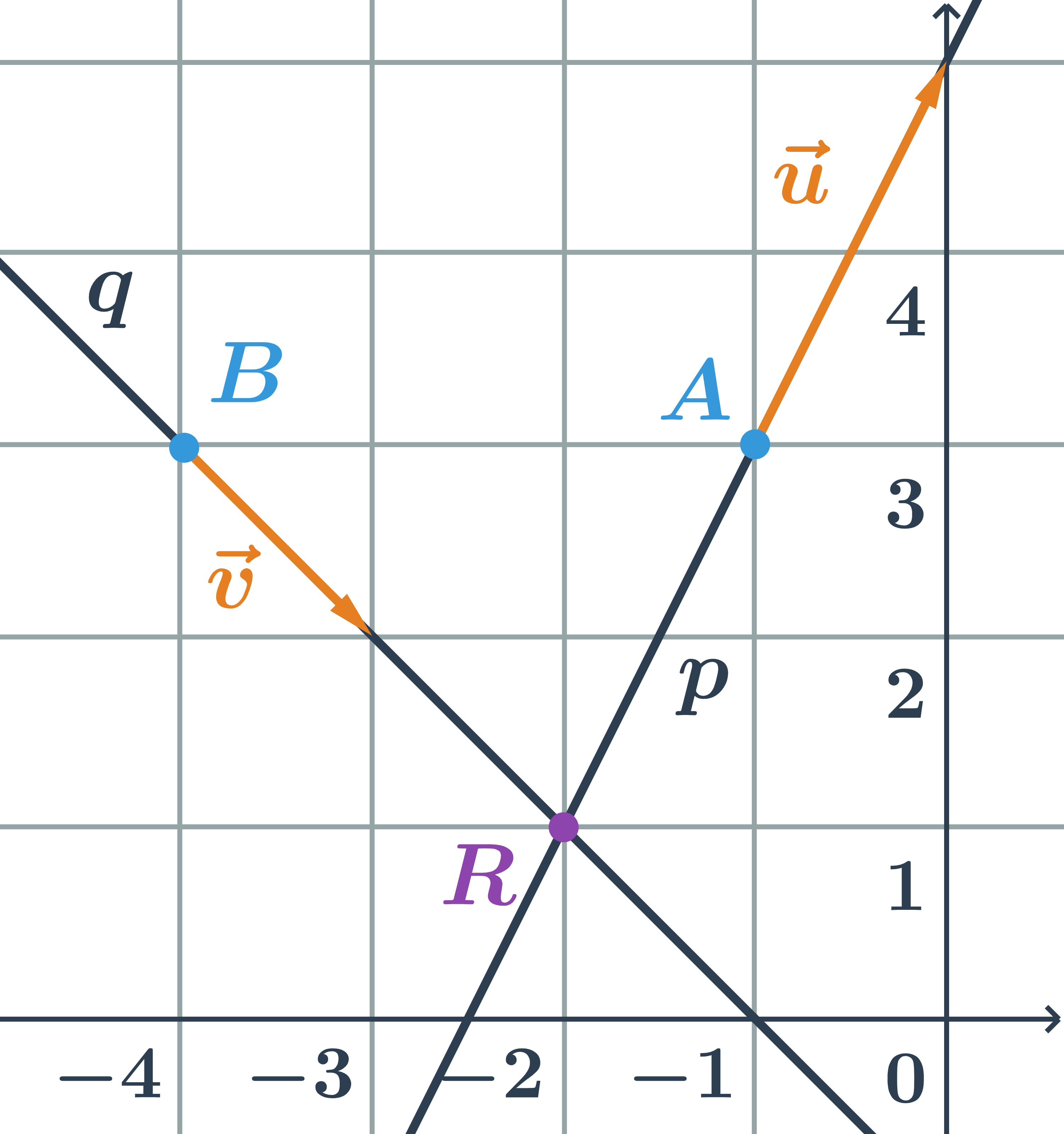
Rôznobežky zadané parametrickými rovnicami
Určite vzájomnú polohu priamok p, q zadaných parametricky:
p: \begin{array}{rrl}x&=&-1+t\\y&=&\hspace{0.25cm}3+2t\\&&\hspace{0.25cm}t\in\mathbb{R}\end{array} \hspace{0.5cm}q: \begin{array}{rrl}x&=&-4+s\\y&=&\hspace{0.25cm}3-s\\&&\hspace{0.25cm}s\in\mathbb{R}\end{array}
- smerový vektor priamky p:\hspace{0.25cm}\vec{u}=(1;2)
- smerový vektor priamky q:\hspace{0.25cm}\vec{v}=(1;-1)
- Priamky p a q sú rôznobežné, pretože ich smerové vektory nie sú kolineárne.
Priesečník priamok spĺňa rovnice oboch priamok, teda každú z jeho súradníc je možné vyjadriť dvomi spôsobmi, dostávame nasledujúcu sústavu rovníc: \begin{array}{lrr}-1+t&=&-4+s\\\hspace{0.25cm}3+2t&=&3-s\end{array}
- Sústavu môžeme vyriešiť sčítaním oboch rovníc: 2+3t=-1\Rightarrow3+3t=0\Rightarrow t=-1
- Výsledný parameter t dosadíme do parametrických rovníc ktorejkoľvek z priamok a dostaneme súradnice x,y priesečníka.
Priesečník priamok p a q je bod R=[-2;1].
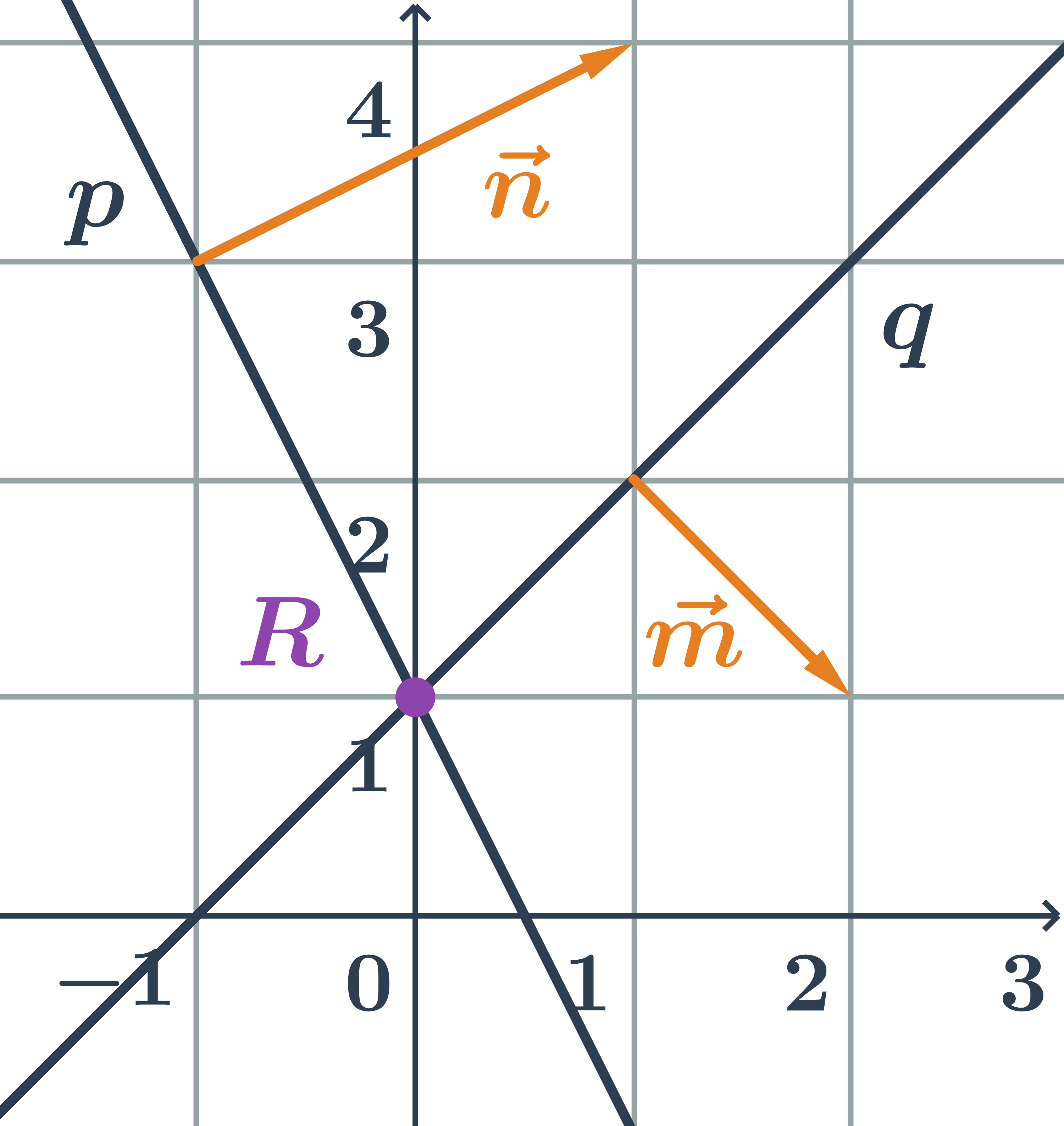
Rôznobežky zadané všeobecnými rovnicami
Určíme vzájomnú polohu dvoch priamok zadaných všeobecnými rovnicami p: 2x+y-1=0 a q:x-y+1=0.
- normálový vektor priamky p:\hspace{0.25cm}\vec{n}=(2;1)
- normálový vektor priamky q:\hspace{0.25cm}\vec{m}=(1;-1)
- Priamky p a q sú rôznobežné, pretože ich normálové vektory nie sú kolineárne.
- Priesečník priamok spĺňa rovnice oboch priamok, teda jeho súradnice sú riešením sústavy: \begin{array}{rrr}2x+y-1&=&0\\x-y+1&=&0\end{array}
- Môžeme vyriešiť sčítaním oboch rovníc: 3x=0\Rightarrow x=0
- Priesečník priamok p a q je bod R=[0;1]
Priamka daná všeobecnou rovnicou a druhá parametricky – prvý príklad
Určite vzájomnú polohu priamok p,q zadaných takto:
\hspace{0.25cm}p: 2x-y+3=0\hspace{0.25cm} \hspace{0.5cm}q: \begin{array}{rrl}x&=&3-2t\\y&=&2-4t\\&&t\in\mathbb{R}\end{array}
- normálový vektor priamky p:\hspace{0.25cm}\vec{n}=(2;-1)
- smerový vektor priamky q:\hspace{0.25cm}\vec{v}=(-2;-4)
- Priamky p a q sú rovnobežné, pretože ich smerové vektory sú kolineárne. Preto je normálový vektor jednej priamky kolmý na smerový vektor druhej priamky.
- Overíme, že priamky nie sú totožné: stačí určiť, či bod, ktorý leží na jednej priamke neleží na priamke druhej.
- Na priamke q leží napríklad bod B=[3;2].
- Na priamke p tento bod neleží, čo zistíme dosadením súradníc bodu B do rovnice priamky: 2\cdot3-2+3\neq 0
- Bod B nespĺňa rovnicu, takže neleží na priamke p \Rightarrow priamky nie sú totožné
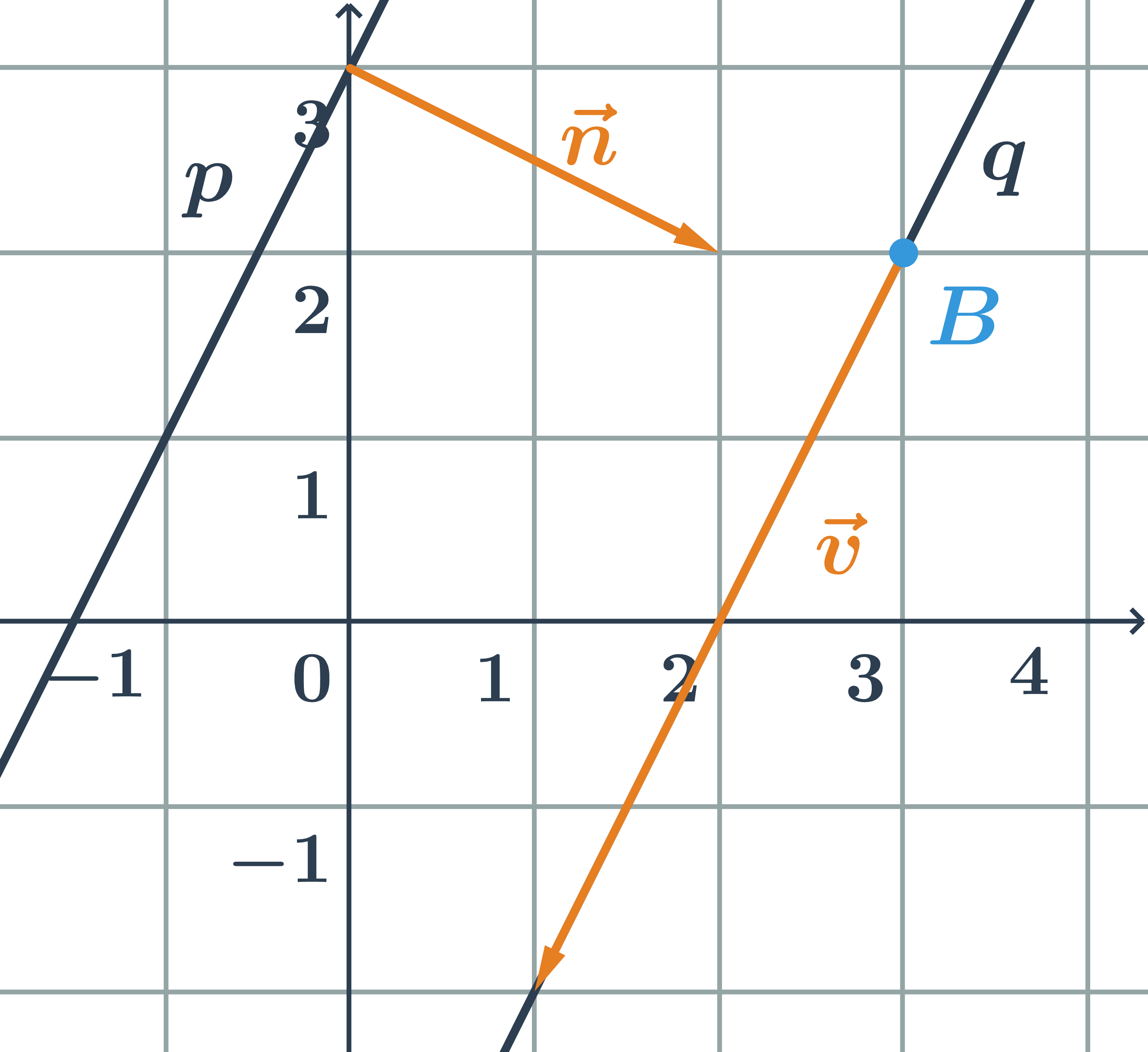
Priamka daná všeobecnou rovnicou a druhá parametricky – druhý príklad
Určite vzájomnú polohu priamok p,q zadaných:
\hspace{0.25cm}p: x-3y+3=0\hspace{0.25cm} \hspace{0.5cm}q: \begin{array}{rrl}x&=&\hspace{0.28cm}1+t\\y&=&-2+2t\\&&\hspace{0.28cm}t\in\mathbb{R}\end{array}
- normálový vektor priamky p:\hspace{0.25cm}\vec{n}=(1;-3)
- smerový vektor priamky q:\hspace{0.25cm}\vec{v}=(1;2)
- Priamky p a q sú rôznobežné, pretože ich smerové vektory nie sú kolineárne. Vyplýva z toho, že normálový vektor jednej priamky nie je kolmý na smerový vektoru druhej priamky.
- Priesečník priamok spĺňa rovnice oboch priamok, teda jeho súradnice nájdeme tak, že parametrické vyjadrenie priamky q dosadíme do všeobecnej rovnice priamky p: \begin{array}{rrl}(1+t)-3(-2+2t)+3&=&0\\1+t+6-6t+3&=&0\\10-5t&=&0\\t&=&2\end{array}
- Priesečník priamok p a q je bod R=[3;2]
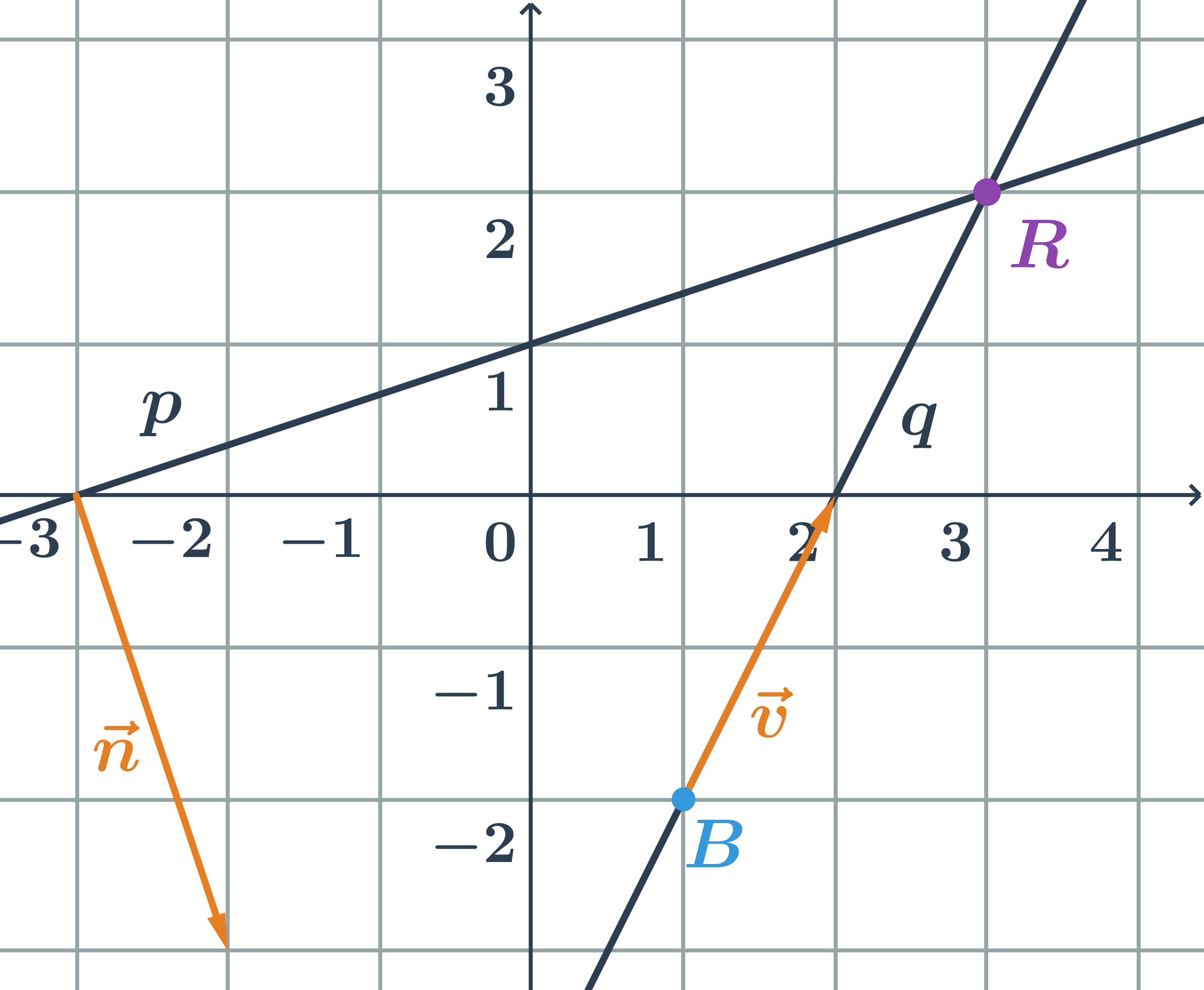
Súvislosť počtu spoločných bodov priamok s počtom riešení sústavy rovníc
Na určenie spoločného bodu (bodov) dvoch priamok, vždy riešime sústavu rovníc. Táto sústava môže mať:
- jedno riešenie – priamky sú rôznobežné
- žiadne riešenie – priamky sú rovnobežné
- nekonečne veľa riešení – priamky sú totožné
Počet spoločných bodov – prvý príklad
Hľadáme priesečník(y) priamok p,q zadaných ako: \hspace{0.25cm}p: x-3y+3=0\hspace{0.25cm} a \hspace{0.25cm}q: \begin{array}{rrl}x&=&\hspace{0.28cm}1+t\\y&=&-2+2t\end{array}
- Dosadíme parametrické vyjadrenie do všeobecnej rovnice a riešime sústavu rovníc:
\begin{array}{rrl}(1+t)-3(-2+2t)+3&=&0\\1+t+6-6t+3&=&0\\10-5t&=&0\\t&=&2\end{array}
- Jedno riešenie \Rightarrow rôznobežné priamky
Počet spoločných bodov – druhý príklad
Hľadáme priesečník(y) priamok p,q zadaných ako: \hspace{0.25cm}p: 2x-y+3=0\hspace{0.25cm} a \hspace{0.25cm}q: \begin{array}{rrl}x&=&3-2t\\y&=&2-4t\end{array}
- Dosadíme parametrické vyjadrenie do všeobecnej rovnice a riešime sústavu rovníc:
\begin{array}{rrl}2(3-2t)-(2-4t)+3&=&0\\6-4t-2+4t+3&=&0\\7&=&0\end{array}
- Žiadne riešenie \Rightarrow rôzne rovnobežné priamky
Počet spoločných bodov – tretí príklad
Hľadáme priesečník(y) priamok p,q zadaných ako: \hspace{0.25cm}p: 2x-y+3=0\hspace{0.25cm} a \hspace{0.25cm}q: \begin{array}{rrl}x&=&3+t\\y&=&9+2t\end{array}
- Dosadíme parametrické vyjadrenie do všeobecnej rovnice a riešime sústavu rovníc:
\begin{array}{rrl}2(3+t)-(9+2t)+3&=&0\\6+2t-9-2t+3&=&0\\0&=&0\end{array}
- Nekonečne veľa riešení \Rightarrow totožné priamky
Vzájomná poloha priamky a bodu v rovine
Bod leží na priamke, ak jeho súradnice vyhovujú rovnici priamky.
- Ak je priamka daná všeobecnou rovnicou, po dosadení súradníc bodu, ktorý na priamke leží do rovnice priamky nastane rovnosť.
- Ak je priamka daná parametricky, po dosadení súradníc bodu vychádza z oboch rovníc rovnaká hodnota parametra t.
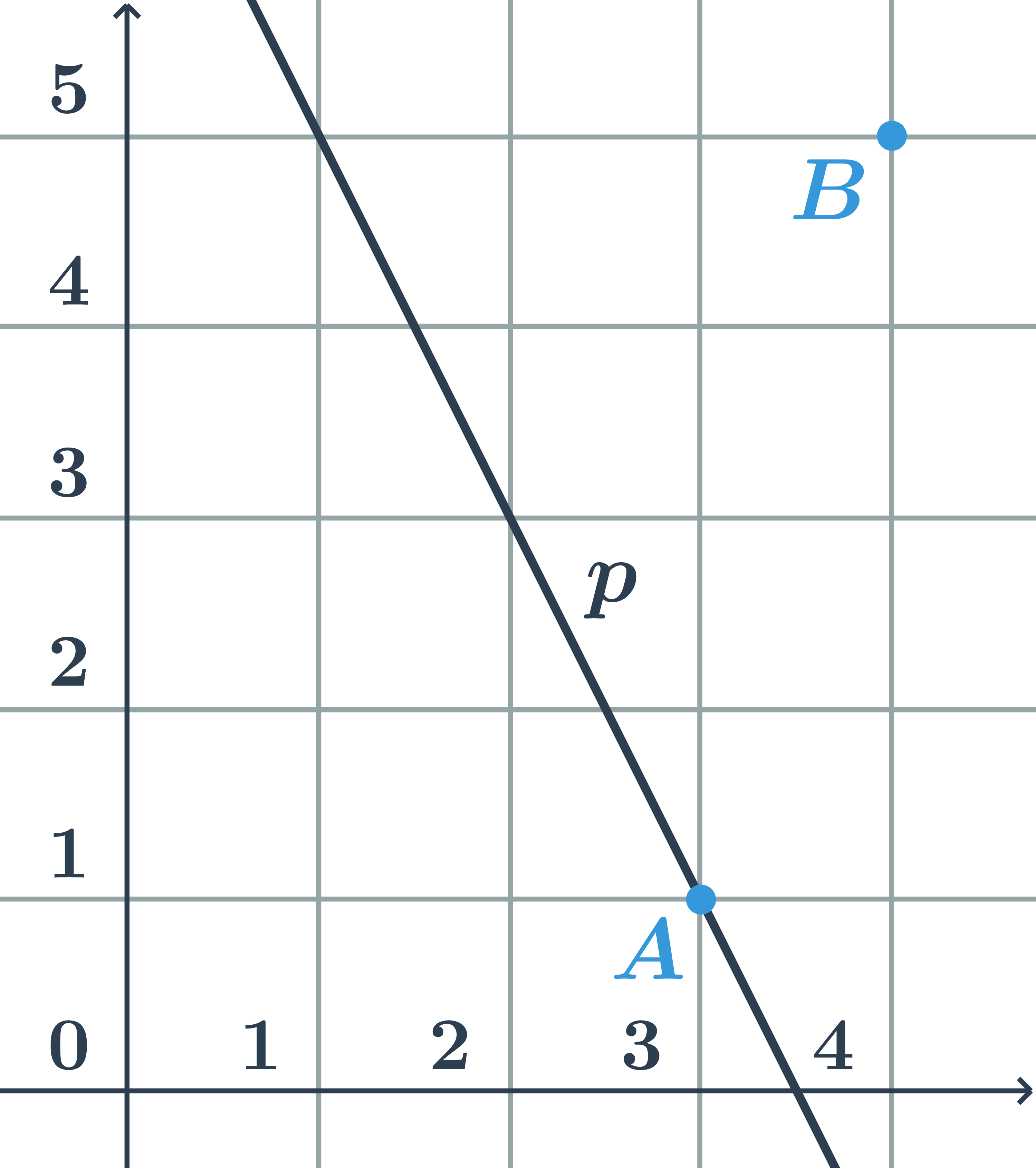
Bod a priamka daná všeobecnou rovnicou
Určite, či body A=[2;3] a B=[-1;2] ležia na priamke p:2x-3y+5=0.
- Do rovnice priamky dosadíme súradnice bodu A=[2;3]:
- 2\cdot 2-3\cdot3+5=0\Rightarrow bod A leží na priamke p
- Do rovnice priamky dosadíme súradnice bodu B=[-1;2]:
- 2\cdot (-1)-3\cdot2+5=-3\Rightarrow bod B neleží na priamke p
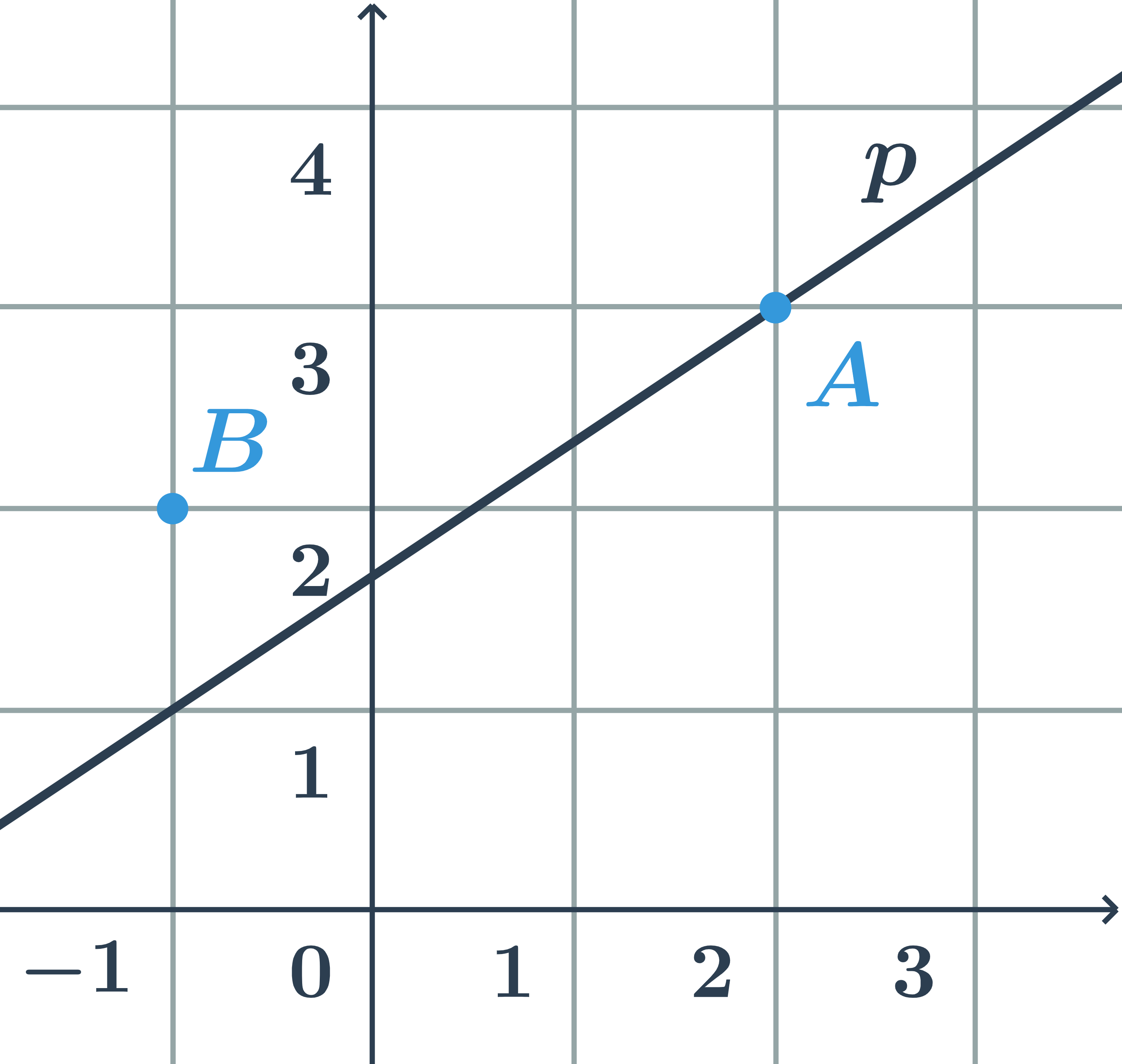
Bod a priamka daná parametricky
Určite, či body A=[3;1] a B=[4;4] ležia na priamke p danej parametricky: \begin{array}{rrl}x&=&2-t\\y&=&3+2t\\&&t\in\mathbb{R}\end{array}
- Do rovníc priamky dosadíme súradnice bodu A=[3;1]:
\begin{array}{rrrr}3&=&2-t&\Rightarrow t=-1\\1&=&3+2t&\Rightarrow t=-1\end{array} \Rightarrow bod A leží na priamke p
- Do rovnice priamky dosadíme súradnice bodu B=[4;5]:
\begin{array}{rrrl}4&=&2-t&\Rightarrow t=-2\\5&=&3+2t&\Rightarrow t=1\end{array}\Rightarrow bod B neleží na priamke p


 Slovenčina
Slovenčina Angličtina
Angličtina Informatika
Informatika Vieme to
Vieme to Nemčina
Nemčina Biológia
Biológia Zemepis
Zemepis Chémia
Chémia Fyzika
Fyzika