Slovenčina
Angličtina
Informatika
Vieme to
Nemčina
Biológia
Zemepis
Chémia
Fyzika
Aritmetika
Zlomky, percentá, desatinné čísla
Geometria
Elementárna algebra
Funkcie
Jednotky, miery
Diskrétna matematika
Finančná gramotnosť
Rozhodovačka
Pexeso
Krok za krokom
Počítanie
Grafár
Porozumenie
Označovanie
Presúvanie
Mriežkovaná
Rozdeľovačka
Pokazená kalkulačka
Roboti
Strieľačka
Príšerky
Preteky
Územia
Tipovačka
Tímovka
Môj účet
Odhlásiť saVýpis prehľadov
Roviny
Prechádzate súhrny informácií k určitým témam. Systémy Vieme sa zameriavajú hlavne na ich precvičovanie. K cvičeniam k jednotlivým podtémam sa dostanete pomocou odkazov nižšie.
Podkapitoly
Rovina je určená tromi bodmi, ktoré neležia na jednej priamke. Z predchádzajúcich kapitol už vieme, že dvojica bodov určuje priamku, prípadne vektor, preto je veľa ďalších spôsobov, ako určiť rovinu:
- bodom a priamkou
- dvomi rôznobežnými priamkami
- dvomi rovnobežnými priamkami
- bodom a dvomi vektormi
V priestore je možné zapísať rovinu ako množinu bodov, ktoré spĺňajú parametrickú rovnicu alebo všeobecnú rovnicu.
Ak máme rovinu popísanú rovnicou, dokážeme určiť vzájomnú polohu roviny a bodu výpočtom.
HoreRoviny: pojmy
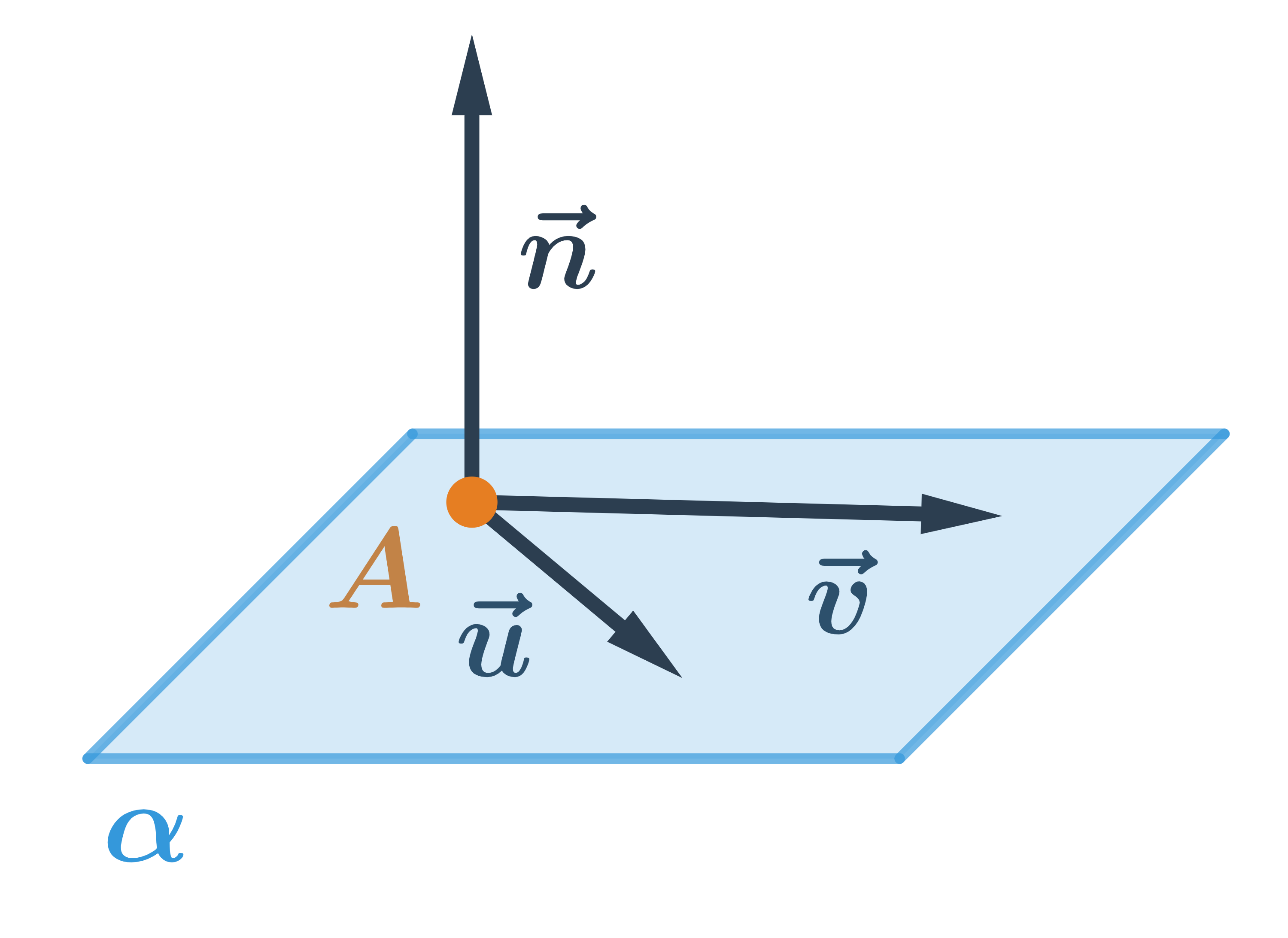
Priamka je jednoznačne určená bodom a dvomi vektormi, ktoré nie sú kolineárne. Na obrázku je rovina \alpha určená bodom A a vektormi \vec{u}, \vec{v}. Každý vektor, ktorý je kolmý na rovinu \alpha sa nazýva normálový vektor roviny \alpha. Na obrázku je normálový vektor \vec{n}.
Parametrické rovnice roviny
Rovina určená bodom A=[a_1;a_2;a_3] a vektormi \vec{u}=(u_1;u_2;u_3) a \vec{v}=(v_1;v_2;v_3) má parametrické rovnice tvaru:
\begin{array}{rrl}x&=&a_1+t\cdot u_1+s\cdot v_1\\y&=&a_2+t\cdot u_2+s\cdot v_2\\z&=&a_3+t\cdot u_3+s\cdot v_3\\&&t,s\in\mathbb{R}\end{array}
Skrátene môžeme vyjadriť \alpha:X=A+t\vec{u}+s\vec{v}, kde t, s nazývame parametrami.
Všeobecná rovnica roviny
Všeobecná rovnica roviny je v tvare ax+by+cz+d=0, kde konštanty a, b, c sú súradnice normálového vektora a d reálne číslo.
Všeobecná rovnica roviny rovnobežnej s osami x a y
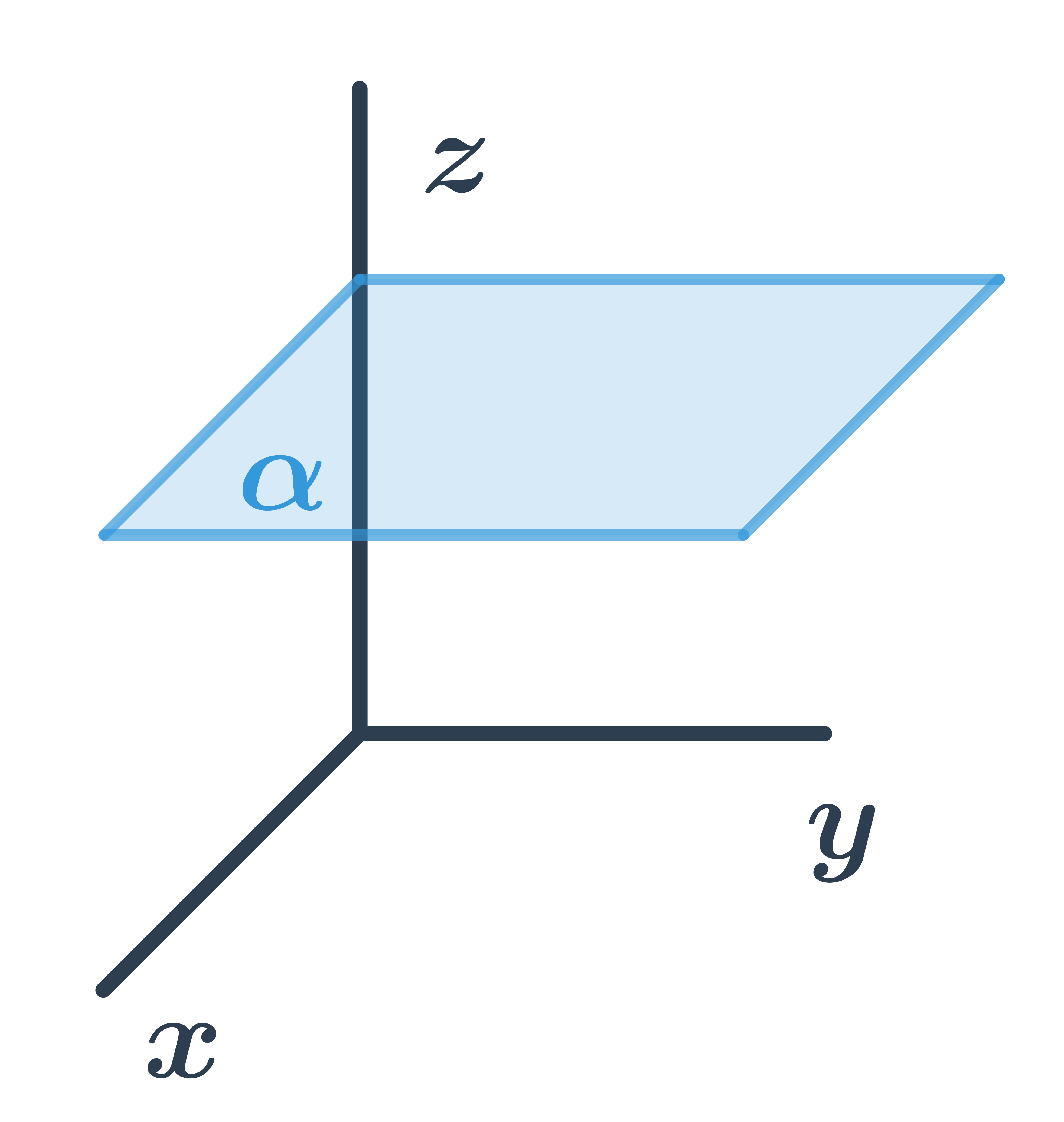
Pre všetky body ležiace v rovine je tretia súradnica rovnaká, teda rovina má všeobecnú rovnicu: z+d=0.
Všeobecná rovnica roviny rovnobežnej s osami x a z
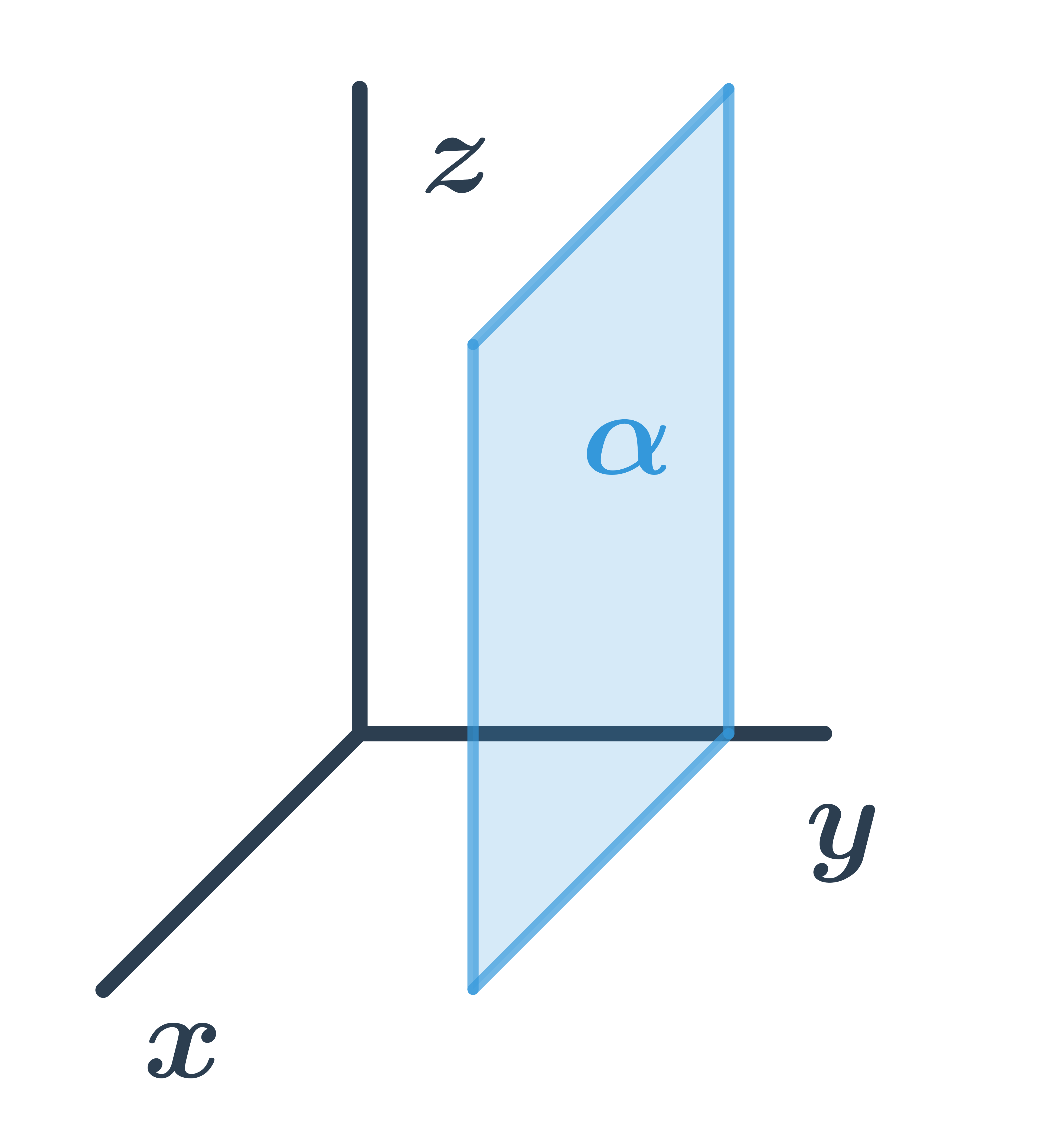
Pre všetky body ležiace v rovine je druhá súradnica rovnaká, teda rovina má všeobecnú rovnicu: y+d=0.
Všeobecná rovnica roviny rovnobežnej s osami y a z
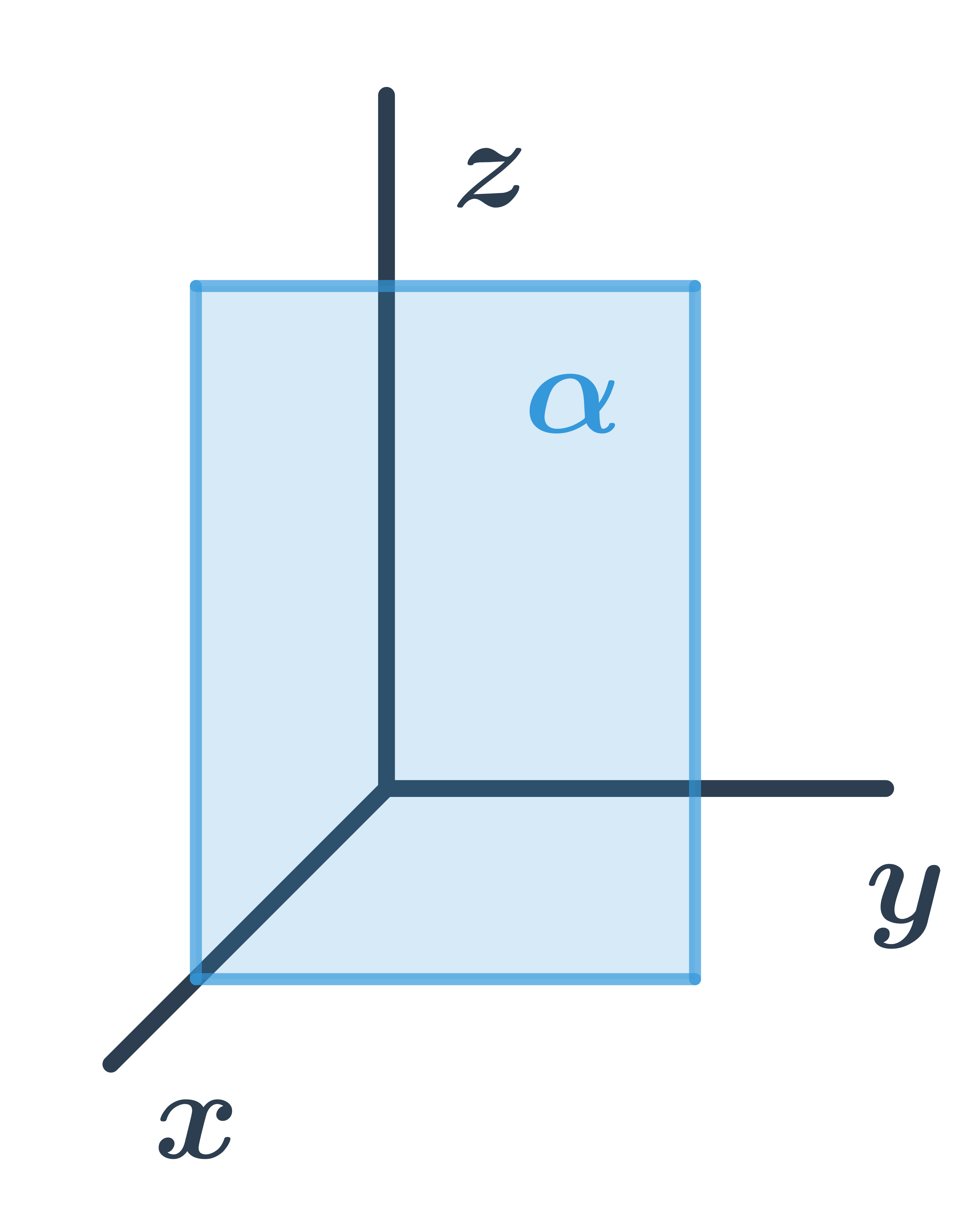
Pre všetky body ležiace v rovine je prvá súradnica rovnaká, teda rovina má všeobecnú rovnicu: z+d=0.
Bod a rovina
Bod M=[m_1;m_2;m_3] leží v rovine, ak jeho súradnice vyhovujú rovnici roviny.
- Ak je rovina daná všeobecnou rovnicou ax+by+cz+d=0, pre súradnice bodu, ktorý leží na priamke platí: a\cdot m_1+b\cdot m_2+c\cdot m_3+d=0
- Ak je rovina daná parametricky, po dosadení súradníc bodu do parametrických rovníc dostaneme sústavu troch rovníc pre dve neznáme t, s, ktorá má presne jedno riešenie (dvojicu reálnych čísel).
Všeobecná rovnica roviny, ktorá prechádza počiatkom
- Rovina prechádza bodom O=[0;0;0], musí teda platiť: a\cdot0+b\cdot0+c\cdot0+d=0\Rightarrow d=0.
- Rovina, ktorá prechádza počiatkom má všeobecnú rovnicu: ax+by+cz=0.
Dve rovnobežné roviny
Normálové vektory dvoch rovnobežných rovín \alpha: a_1x+b_1y+c_1z+d_1=0 a \beta: a_2x+b_2y+c_2z+d_2=0 sú kolineárne, teda súradnice jedného vektora sú k-násobok súradníc druhého vektora. Pre konštanty vo všeobecných rovniciach musí platiť:
\begin{array}{rll}a_2&=&k\cdot a_1\\ b_2&=&k\cdot b_1\\c_2&=&k\cdot c_1\\&&k\in\mathbb{R}\end{array}
Ak by platilo i d_2=k\cdot d_1 roviny sú totožné.
HoreParametrická rovnica roviny
Na určenie parametrických rovníc roviny potrebujeme poznať súradnice jedného bodu a dvoch nekolineárnych vektorov v rovine \alpha. Rovina určená bodom A=[a_1;a_2;a_3] a vektormi \vec{u}=(u_1;u_2;u_3) a \vec{v}=(v_1;v_2;v_3) má parametrické rovnice tvaru:
\begin{array}{rrl}x&=&a_1+t\cdot u_1+s\cdot v_1\\y&=&a_2+t\cdot u_2+s\cdot v_2\\z&=&a_3+t\cdot u_3+s\cdot v_3\\&&t,s\in\mathbb{R}\end{array}
Skrátene môžeme vyjadriť \alpha:X=A+t\vec{u}+s\vec{v}, kde t,s \in \mathbb{R} sú parametre.
Parametrické rovnice roviny určenej tromi bodmi
Určite parametrické rovnice roviny \alpha určenej body A=[3;2;1], B=[1;3;4], C=[2;-3;3].
- rovina \alpha je určená bodom A a vektormi \vec{u}=\overrightarrow{AB}, \vec{v}=\overrightarrow{AC}:
- \vec{u}=\overrightarrow{AB}=B-A=(-2;1;3)
- \vec{v}=\overrightarrow{AC}=C-A=(-1;-5;2)
- parametrické rovnice roviny \alpha sú:
\begin{array}{rrl}x&=&3-2t-s\\y&=&2+t-5s\\z&=&1+3t+2s\\&&t,s\in\mathbb{R}\end{array}
Parametrické rovnice roviny určenej bodom a dvomi vektormi
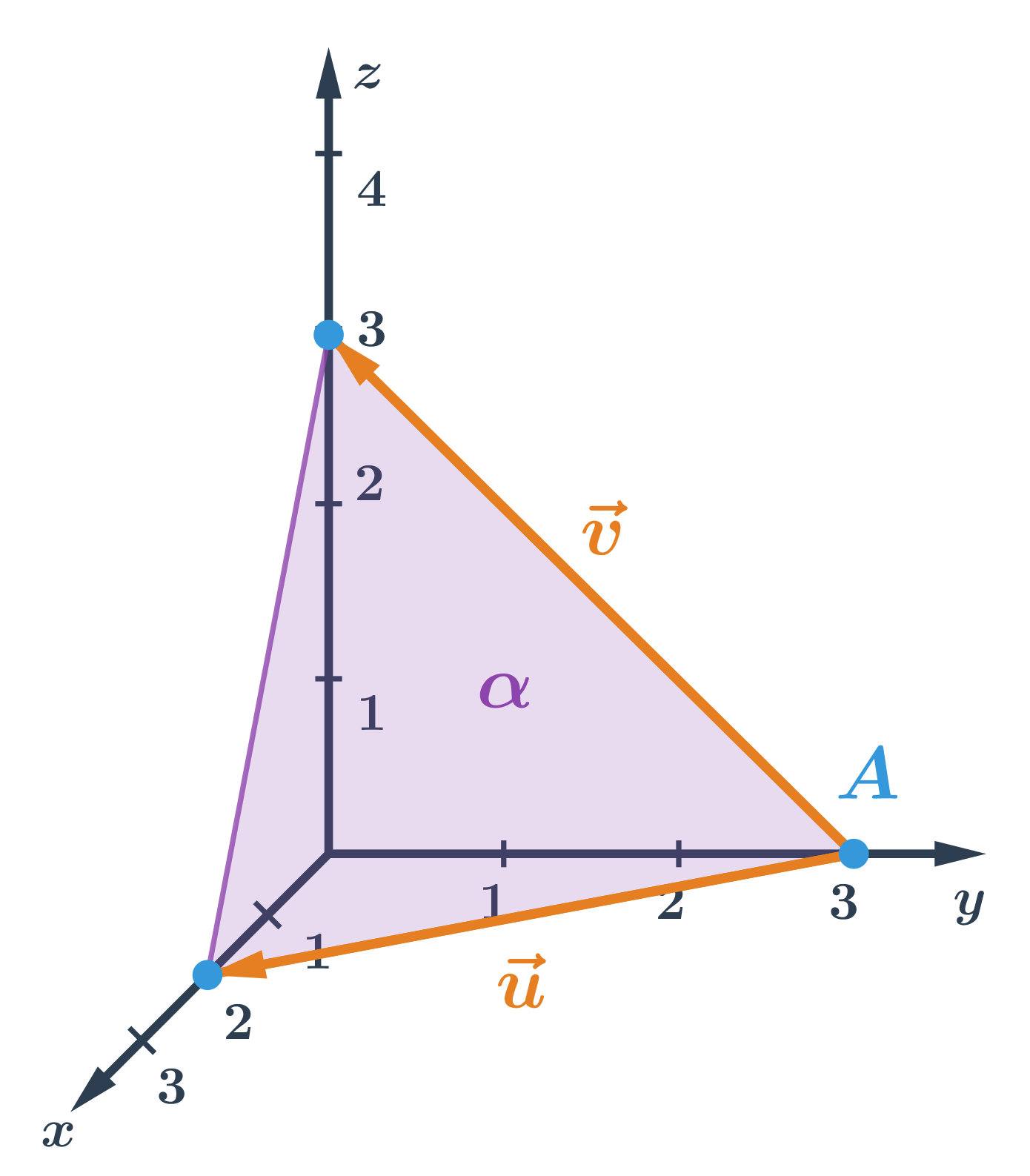
- rovina \alpha je určená bodom A a vektormi \vec{u}, \vec{v}
- súradnice určíme z obrázka:
- A=[0;3;0],
- \vec{u}=(2;-3;0),
- \vec{v}=(0;-3;3)
- parametrické rovnice roviny \alpha sú:
\begin{array}{rrl}x&=&2t\\y&=&3-3t-3s\\z&=&3s\\&&t,s\in\mathbb{R}\end{array}
Parametrické rovnice roviny určenej rôznobežkami p a q
Určite parametrické rovnice roviny určenej dvomi rôznobežkami s nasledujúcimi parametrickými rovnicami:
p:\begin{array}{rrl}x&=&2+3t\\y&=&1+2t\\z&=&4-4t\\&&t\in\mathbb{R}\end{array}, q:\begin{array}{rrl}x&=&2+4s\\y&=&1-2s\\z&=&4-5s\\&&s\in\mathbb{R}\end{array}
- rovina \alpha je určená spoločným bodom rôznobežiek a smerovými vektormi priamok p a q
- spoločný bod rôznobežiek: R=[2;1;4],
- smerový vektor priamky p:\vec{u}=(3;2;4),
- smerový vektor priamky q:\vec{v}=(4;-2;-5)
- parametrické rovnice roviny \alpha sú:
\begin{array}{rrl}x&=&2+3t+4s\\y&=&1+2t-2s\\z&=&4-4t-5s\\&&t,s\in\mathbb{R}\end{array}
Všeobecná rovnica roviny
Všeobecná rovnica roviny má tvar ax+by+cz+d=0, kde konštanty a, b, c sú súradnice normálového vektora a d reálne číslo. Normálový vektor \vec{n}=(a;b;c) je vektor kolmý na danú rovinu.
Všeobecná rovnica roviny určenej bodom a normálovým vektorom
Určite všeobecnú rovnicu roviny \alpha určenej bodom A=[-3;1;2] a normálovým vektorom \vec{n}=(2;3;-4).
- Súradnice normálového vektora sú konštanty a, b, c vo všeobecnej rovnici roviny, preto všeobecná rovnica bude mať tvar: 2x+3y-4z+d=0
- Konštantu d určíme dosadením súradníc bodu A=[-3;1;2] do všeobecnej rovnice: 2\cdot(-3)+3\cdot1-4\cdot 2+d=0\Rightarrow -11+d=0\Rightarrow d=11
- Všeobecná rovnica roviny \alpha je: 2x+3y-4z+11=0
Všeobecná rovnica roviny danej bodom a rovnobežnej s inou rovinou
Všeobecná rovnica roviny \alpha, ktorá prechádza bodom A=[2;3;1] a je rovnobežná s rovinou \beta:3x+y+4z+1=0.
- Dve rovnobežné roviny majú rovnaký normálový vektor, súradnice normálového vektoru sú súradnice a, b, c vo všeobecnej rovnici roviny.
- Preto všeobecná rovnica hľadanej roviny \alpha bude mať tvar: 3x+y+4z+d=0
- Konštantu d určíme dosadením súradníc bodu A=[2;3;1] do všeobecnej rovnice: 3\cdot2+3+4\cdot 1+d=0\Rightarrow 13+d=0\Rightarrow d=-13
- Všeobecná rovnica roviny \alpha je: 3x+y+4z-13=0
Vzájomná poloha bodu a roviny
Bod leží v rovine, ak jeho súradnice vyhovujú rovnici roviny. Ak je rovina daná všeobecnou rovnicou, po dosiahnutí súradnic bodu do rovnice roviny nastane rovnosť. Ak je rovina daná parametricky, po dosiahnutí súradníc bodu dostaneme sústavu troch rovníc pre dve neznáme, ktorá má presne jedno riešenie.
Bod a rovina daná všeobecnou rovnicou
Určite, či body A=[3;4;2] a B=[1;3;0] ležia v rovine \alpha danej všeobecnou rovnicou 2x-y+3z+1=0.
- Do rovnice roviny dosadíme súradnice bodu A=[3;4;2].
- 2\cdot 3-4+3\cdot2+1=0\Rightarrow9\neq 0, teda bod A neleží v rovine \alpha.
- Do rovnice priamky dosadíme súradnice bodu B=[1;3;0].
- 2\cdot 1-3+3\cdot0+1=0\Rightarrow0=0, teda bod B leží v rovine \alpha.
Bod a rovina daná parametricky
Určite, či body A=[2;3;4] a B=[0;2;2] ležia v rovine \alpha danej parametrickými rovnicami:
\begin{array}{rrl}x&=&1-t+s\\y&=&2+t+s\\z&=&3-t+s\\&&t,s\in\mathbb{R}\end{array}
- Do rovníc roviny dosadíme súradnice bodu A=[1;3;4]: \begin{array}{rrrr}2&=&1-t+s\\3&=&2+t+s\\4&=&3-t+s\\\end{array}
- Z prvých dvoch rovníc určíme hodnoty t a s, dosadením do tretej rovnice zistíme, či sú nájdené hodnoty riešením sústavy a teda či bod leží na priamke:
- prvú a druhú rovnicu sčítame: 5=3+2s\Rightarrow s=1
- hodnotu s=1 dosadíme do prvej rovnice: 1=1-t+1\Rightarrow t=1
- hodnoty s=1 a t=1 dosadíme do tretej rovnice: 4=3-1+1. Táto rovnosť neplatí, teda bod A neleží v rovine \alpha.
- Do rovníc roviny dosadíme súradnice bodu B=[0;-3;2]: \begin{array}{rrrr}0&=&1-t+s\\-3&=&2+t+s\\2&=&3-t+s\\\end{array}
- Z prvých dvoch rovníc určíme hodnoty t a s, dosadením do tretej rovnice zistíme, či sú nájdené hodnoty riešením sústavy a teda či bod leží na priamke:
- prvú a druhú rovnicu sčítame: -3=3+2s\Rightarrow s=-3
- hodnotu s=-3 dosadíme do prvej rovnice: 0=1-t-3\Rightarrow t=-2
- hodnoty s=-3 a t=-2 dosadíme do tretej rovnice: 2=3-(-2)-3. Táto rovnosť platí, teda bod B leží v rovine \alpha.
