Výpis prehľadov
Uhly
Podkapitoly
Uhol je časť roviny vymedzená dvomi polpriamkami. Veľkosť uhla meriame najčastejšie v stupňoch, pričom plný uhol má veľkosť 360°. Uhly využívame v mnohých oblastiach geometrie a majú bohaté praktické využitie vo fyzike, navigácii (azimuty) a v podstate kdekoľvek, kde sa niečo stavia.
Pri práci s uhlami je prvý krok základné rozpoznávanie uhlov – potrebujeme získať základnú predstavu o uhloch a schopnosť odhadnúť veľkosť uhlu podľa obrázka. Ďalší krok je potom znalosť pojmov súvisiacich s uhlami, medzi ktoré patrí napríklad uhol ostrý, tupý, pravý, plný, vrcholový alebo striedavý.
Na získanie zbehlosti v práci s uhlami môže poslúžiť atraktívne cvičenie Korytnačia grafika na Vieme informatiku.
Keď zvládneme základy práce s uhlami, môžeme sa pustiť do práce s uhlami v rovinových objektoch:
HoreUhly v trojuholníku
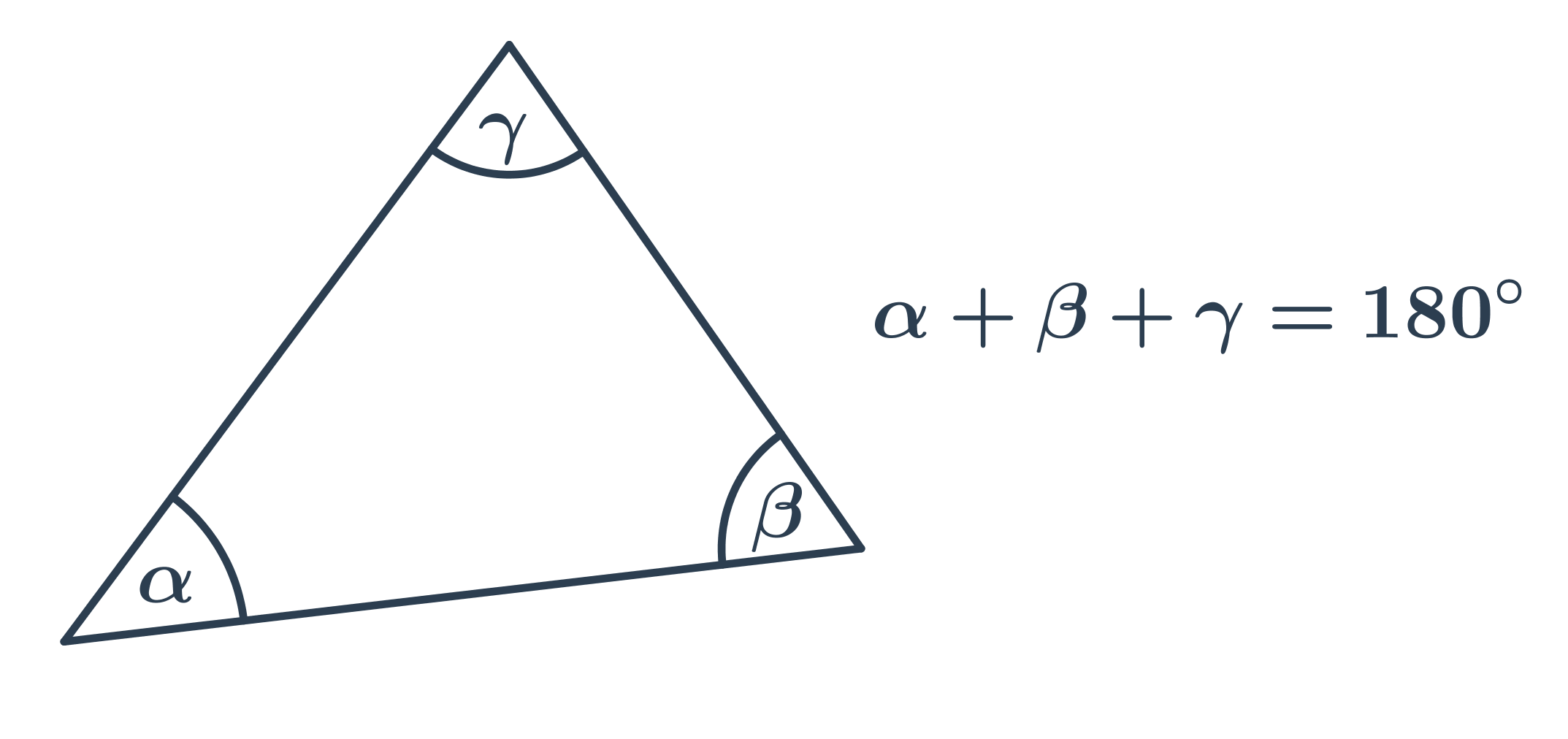
Špeciálne prípady:
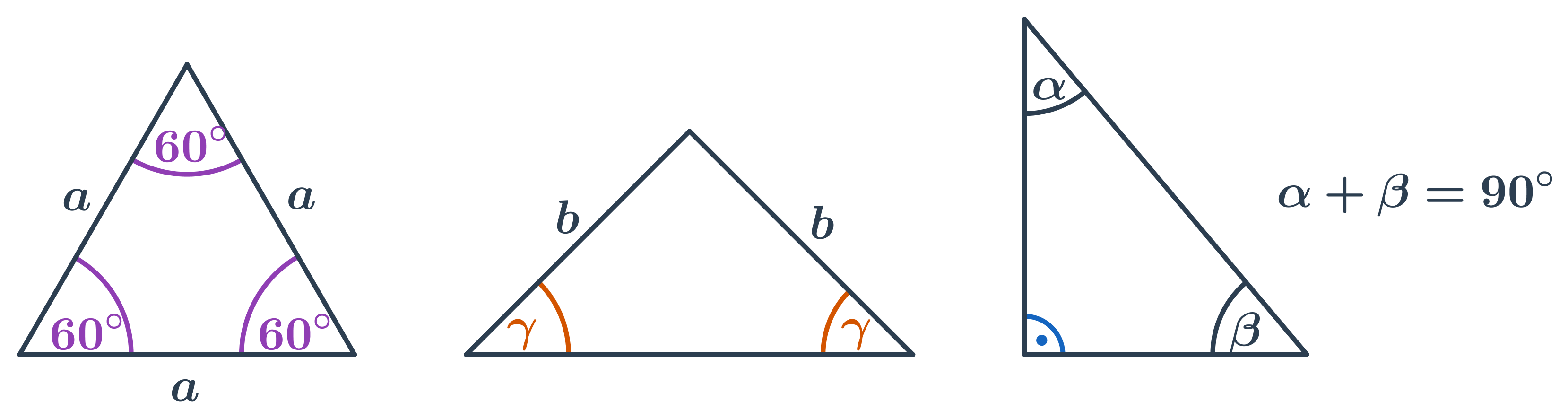
- V rovnostrannom trojuholníku majú všetky vnútorné uhly veľkosť 60°.
- V rovnoramennom trojuholníku sú oba uhly pri základni rovnaké.
- V pravouhlom trojuholníku je veľkosť jedného uhla 90°, súčet veľkostí zvyšných dvoch uhlov je tiež 90°.
Pri výpočte je možné využiť aj vrcholové a vedľajšie uhly.
Príklad: Určite veľkosť oranžového uhla.
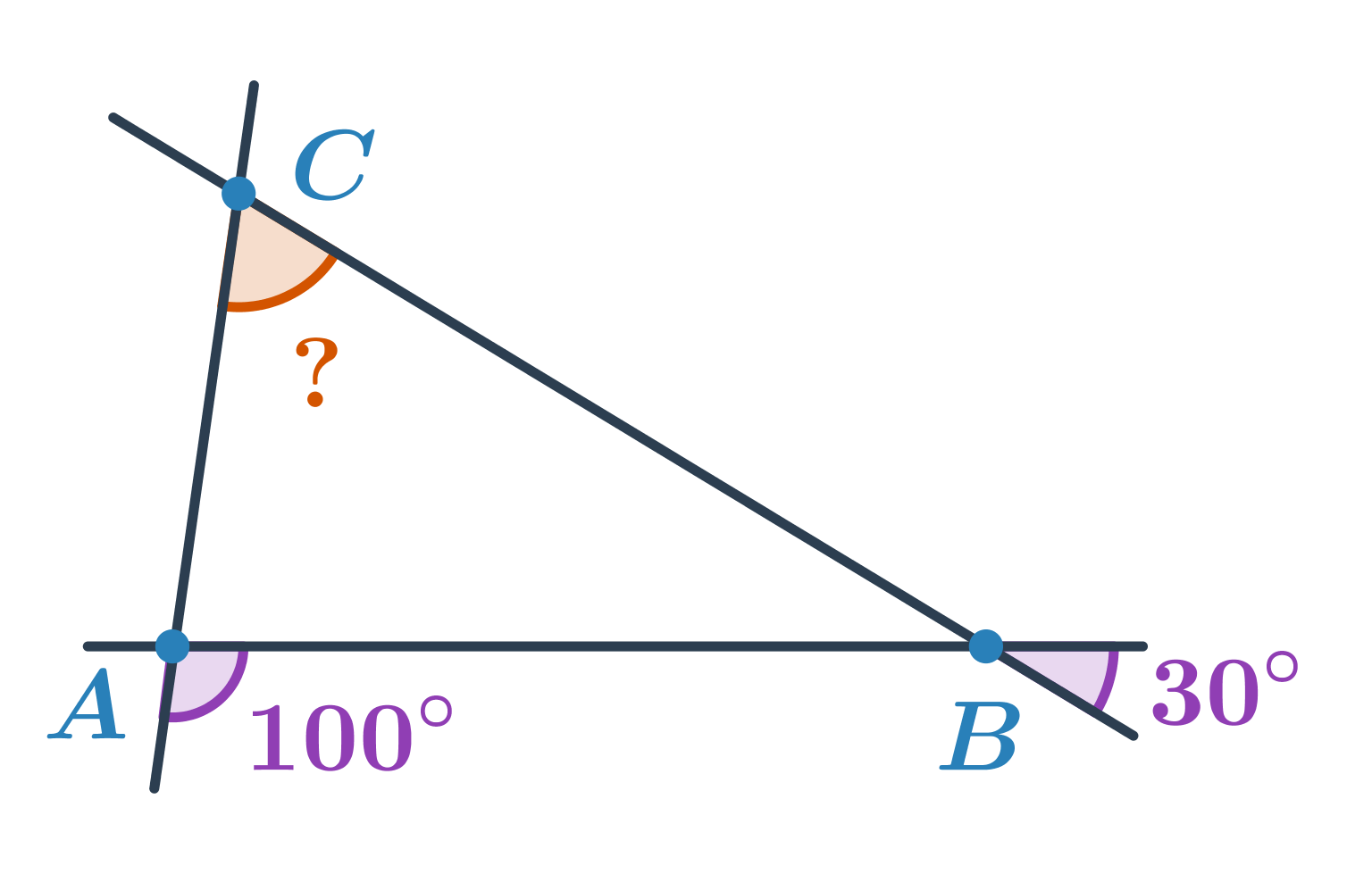
Uhol s vrcholom B tvorí s uhlom s veľkosťou 30° dvojicu vrcholových uhlov. Jeho veľkosť je teda 30°. Uhol pri vrchole A tvorí s uhlom s veľkosťou 100° dvojicu vedľajších uhlov. Jeho veľkosť je teda 180°-100°=80°. Pre veľkosť neznámeho uhla pri vrchole C potom platí: 180°-80°-30°=70°
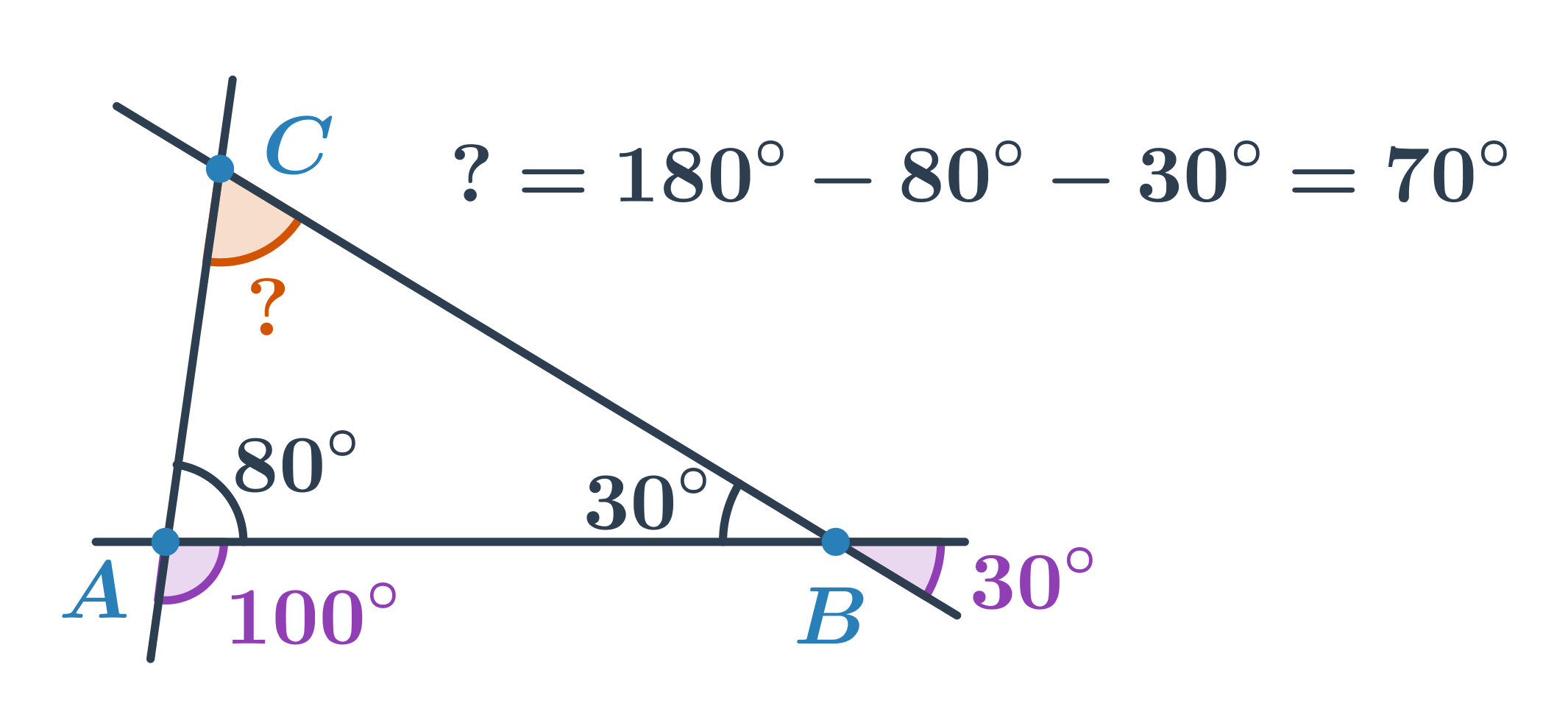
Uhly vo štvoruholníku
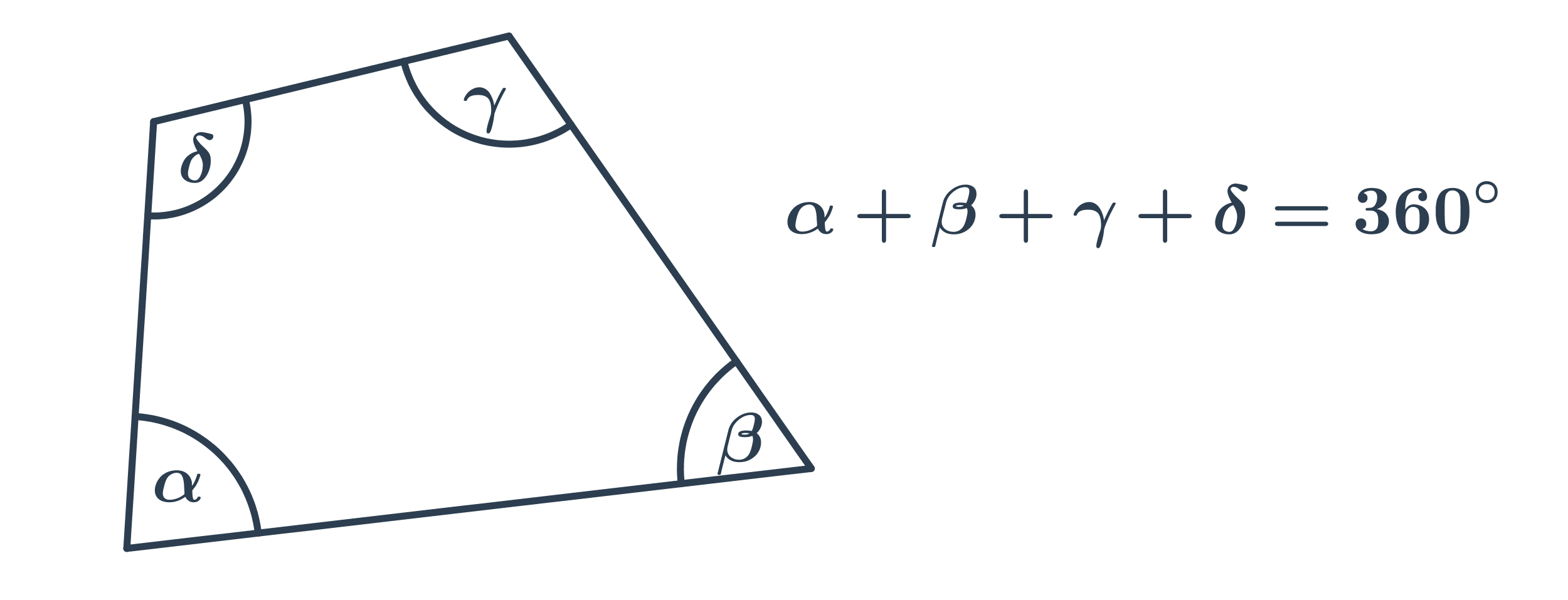
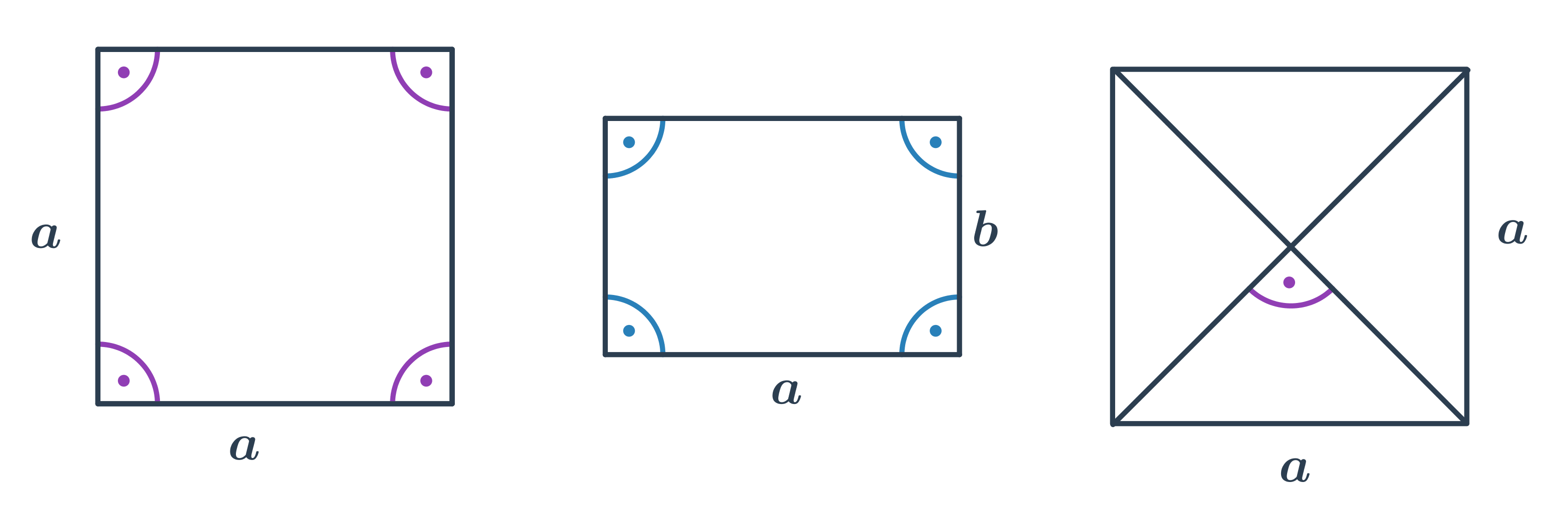
Štvorec, obdĺžnik
- V štvorci aj obdĺžniku je veľkosť všetkých vnútorných uhlov 90°.
- V štvorci zvierajú uhlopriečky uhol s veľkosťou 90°.
Rovnobežník
- Protiľahlé uhly majú rovnakú veľkosť.
- Súčet veľkostí susedných uhlov je 180°.
- Špeciálnym prípadom rovnobežníka je kosoštvorec, ktorého uhlopriečky zvierajú pravý uhol.
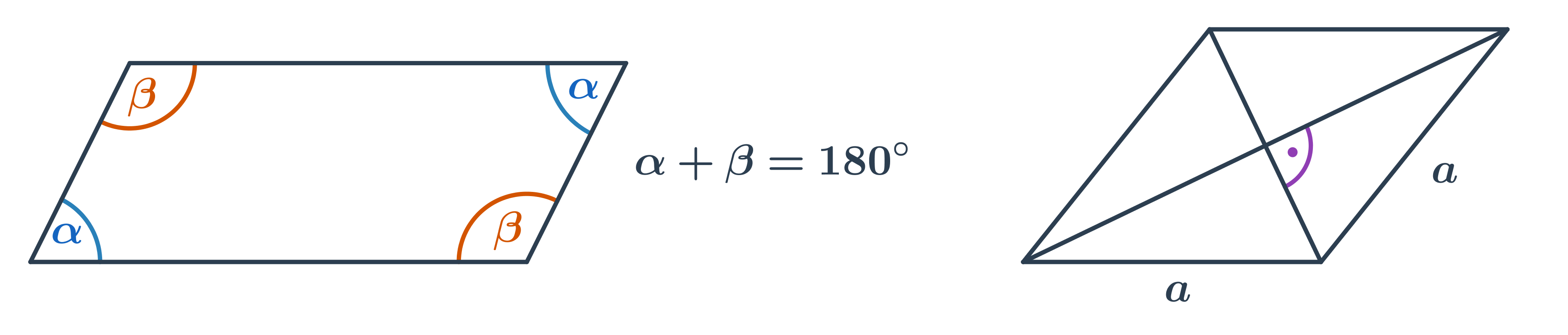
Lichobežník
- Súčet veľkostí vnútorných uhlov pri ramenách je 180°.
- V rovnoramennom lichobežníku sú uhly pri základniach zhodné.
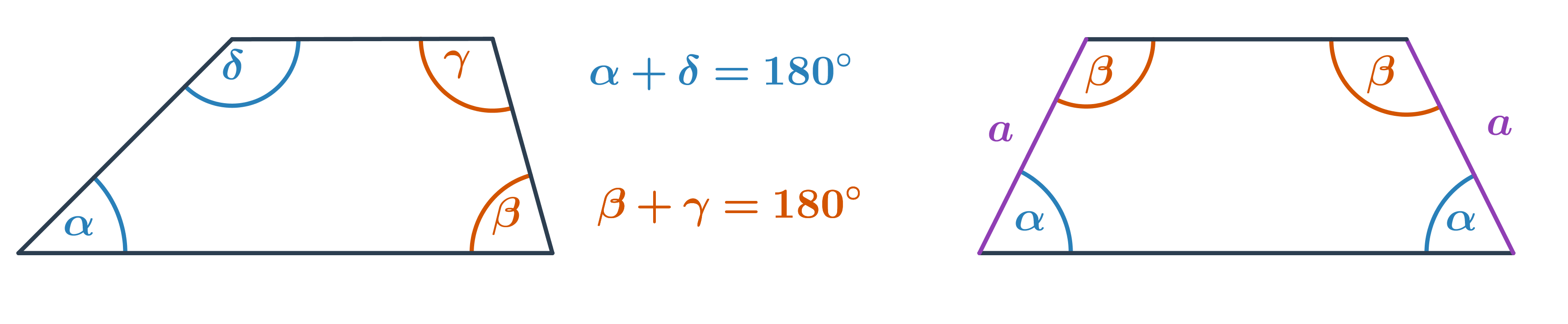
Pri výpočte neznámeho uhla môžeme tiež daný štvoruholník rozdeliť na niekoľko trojuholníkov a tiež je možné využiť aj vrcholové a vedľajšie uhly.
Príklad: Určite veľkosť oranžového uhla v rovnobežníku ABCD.
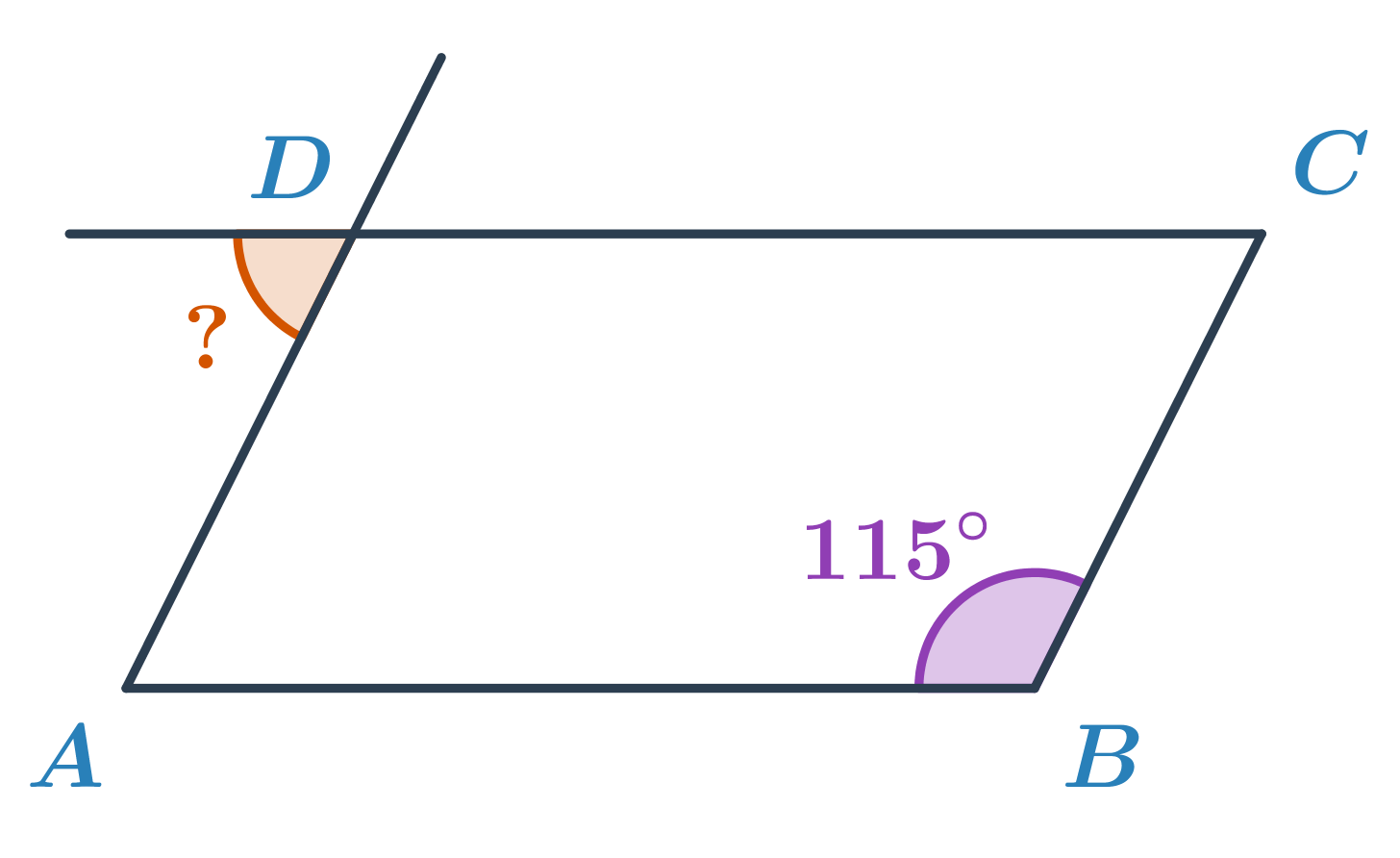
V rovnobežníku majú protiľahlé uhly rovnakú veľkosť, uhol ADC má teda veľkosť 115°. Uhol ADC tvorí s neznámym uhlom dvojicu vedľajších uhlov. Veľkosť neznámeho uhla je teda 180°-115°=65°.
HoreUhly a mnohouholníky
Súčet vnútorných uhlov vo všeobecnom mnohouholníku s n stranami (teda n-uholníku) je 180^\circ\cdot(n-2). Napríklad v päťuholníku je súčet vnútorných uhlov 180^\circ(5-2)=540^\circ. Každý vnútorný uhol potom môže mať inú veľkosť.
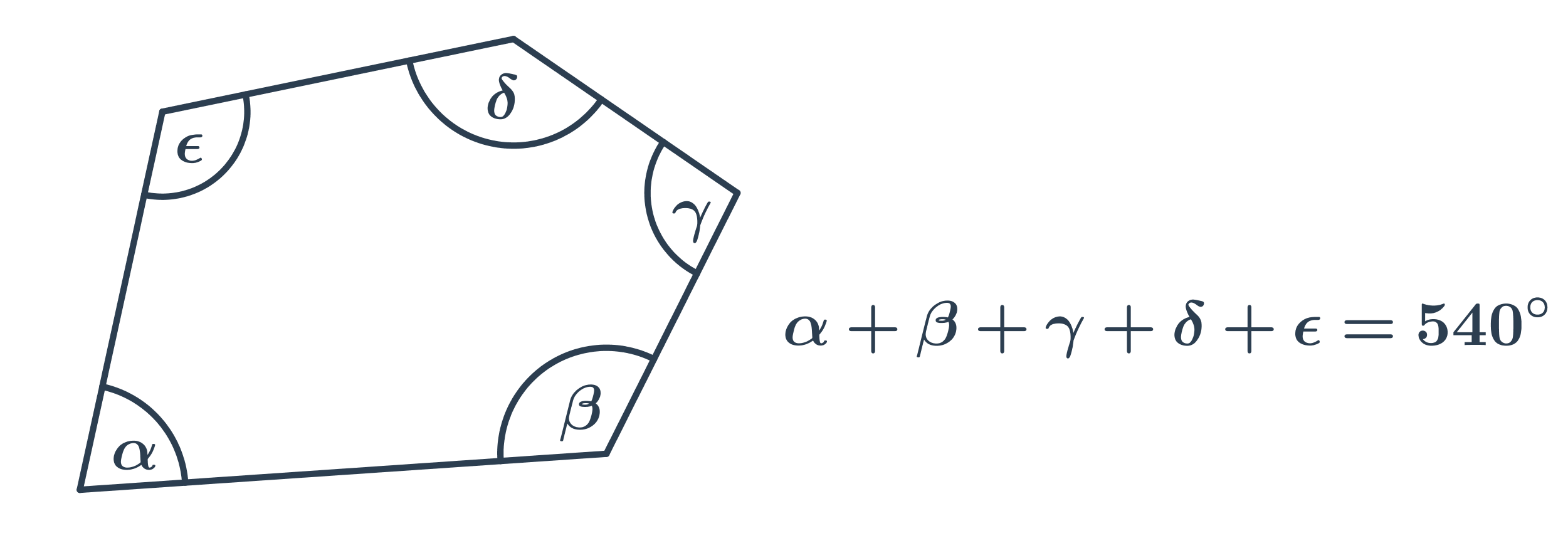
Pravidelné mnohouholníky
- Každý vnútorný uhol v pravidelnom mnohouholníku s n vrcholmi má veľkosť 180^\circ\cdot\frac{n-2}{n}. Napríklad v pravidelnom osemuholníku má každý vnútorný uhol veľkosť 180^\circ\cdot\frac{8-2}{6}=135^\circ.
- Veľkosť stredového uhla pravidelného n-uholníka je \frac{360^\circ}{n}. Napríklad v pravidelnom osemuholníku má každý stredový uhol veľkosť \frac{360^\circ}{8}=45^\circ.
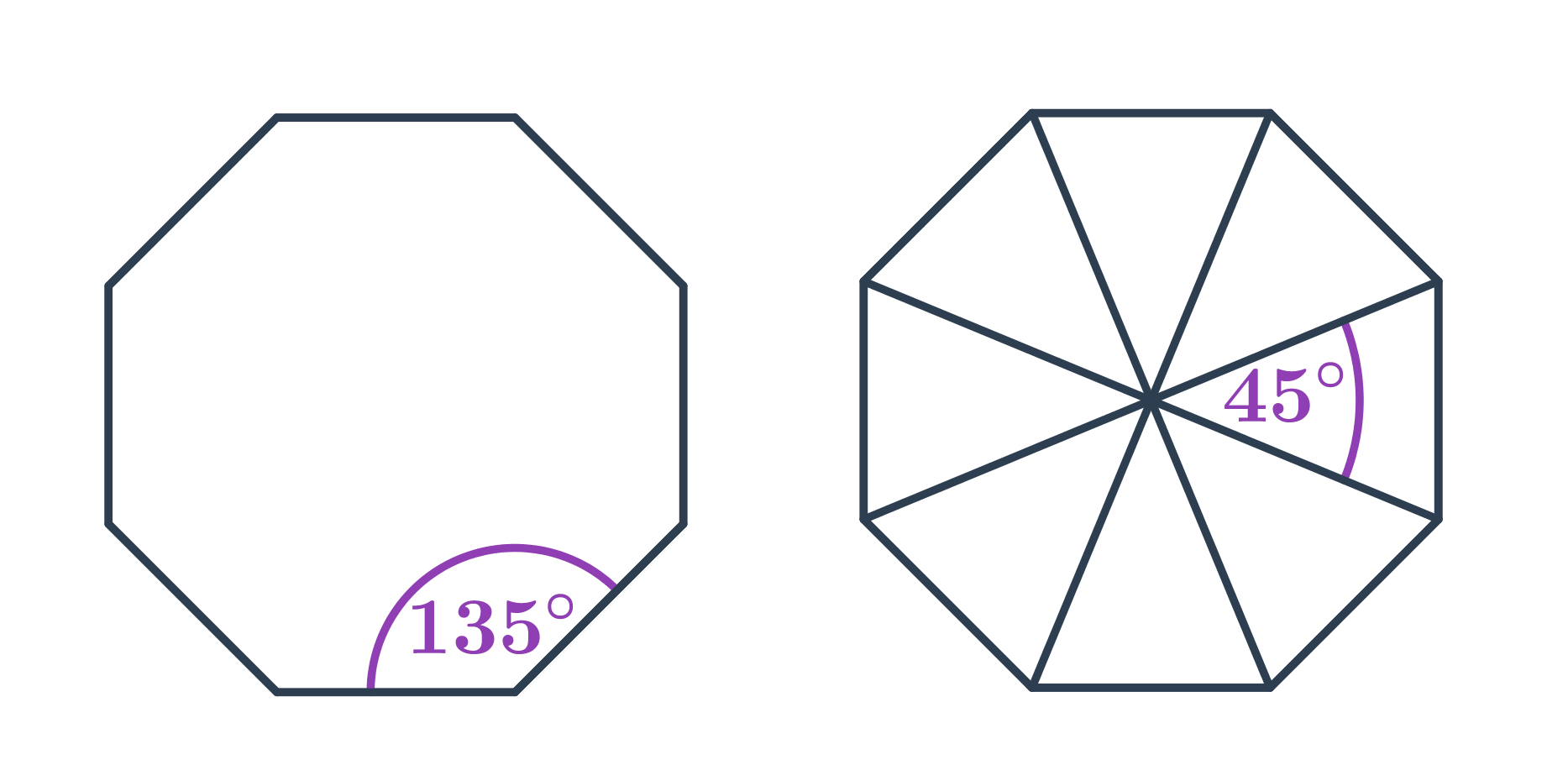
Pri výpočte neznámeho uhla v mnohouholníku je možné využiť aj vrcholových a vedľajších uhlov.
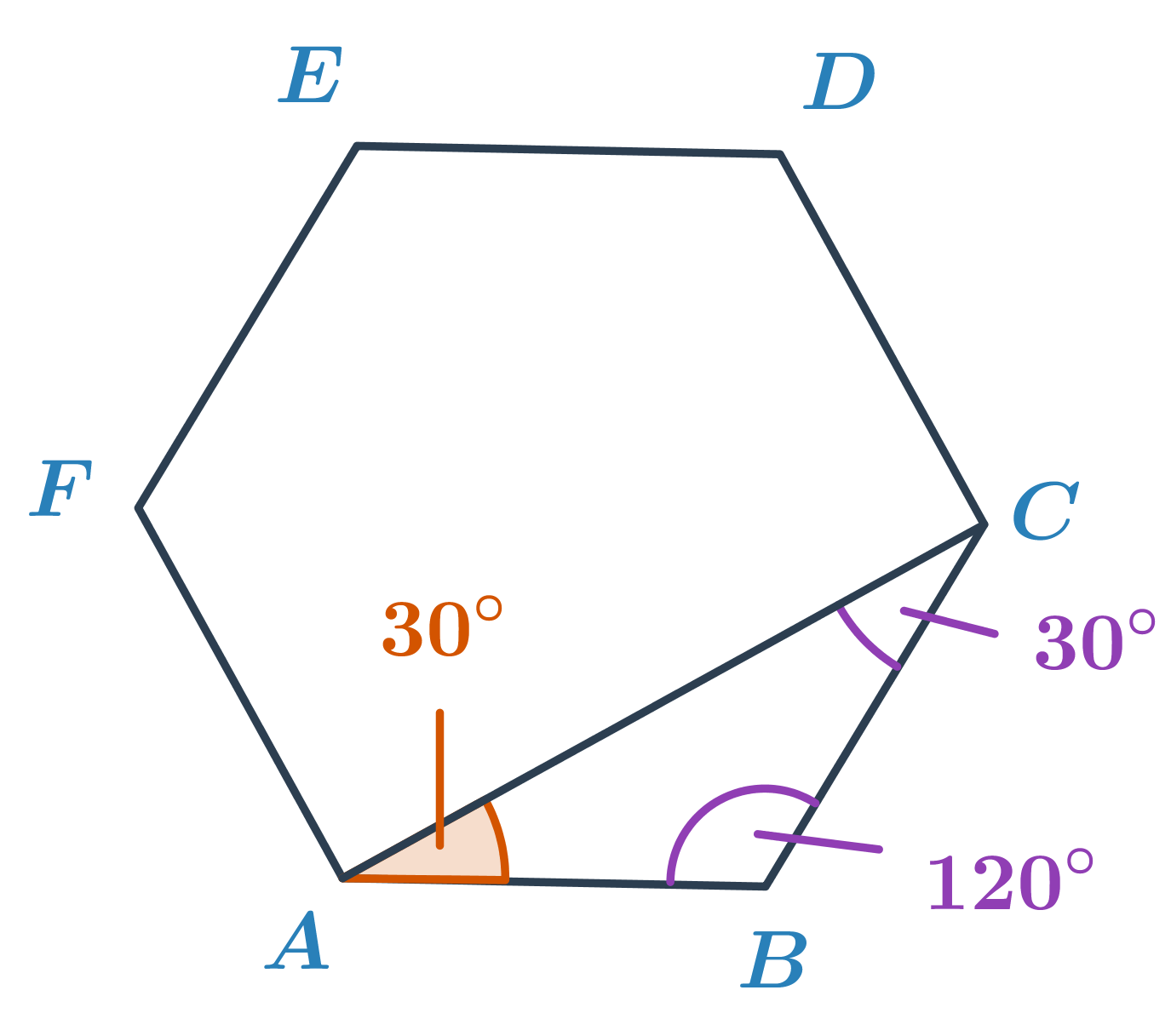
Príklad: Určite veľkosť oranžového uhla v pravidelnom šesťuholníku ABCDEF.
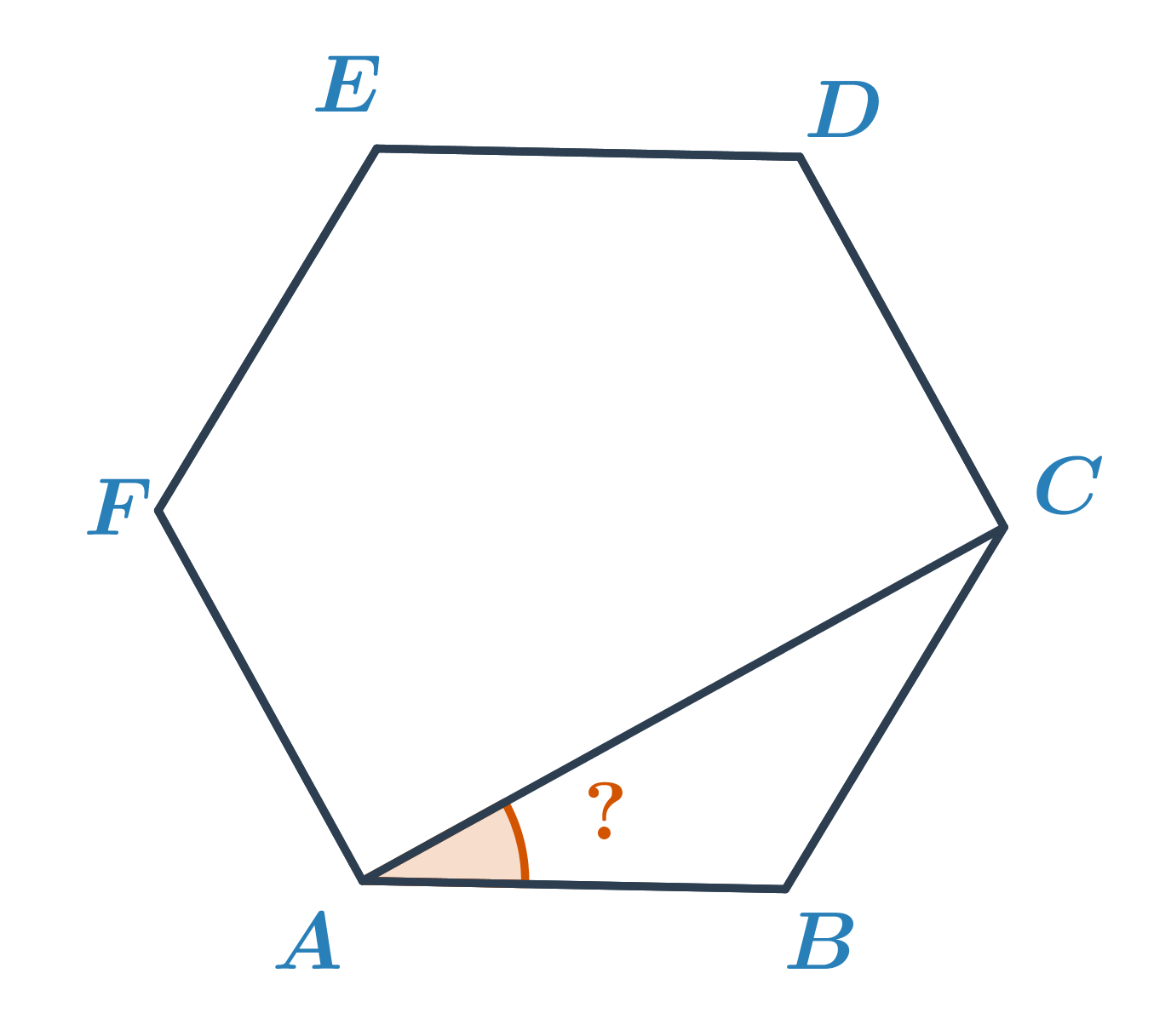
V pravidelnom šesťuholníku má každý uhol rovnakú veľkosť, a to 180^\circ\cdot\frac{6-2}{6}=120^\circ. Uhol ABC má teda veľkosť 120^\circ. Trojuholník ABC je rovnoramenný, uhly pri vrcholoch A a C sú potom zhodné. Ich veľkosť je (180^\circ-120^\circ):2=30^\circ.
Uhly a kružnice
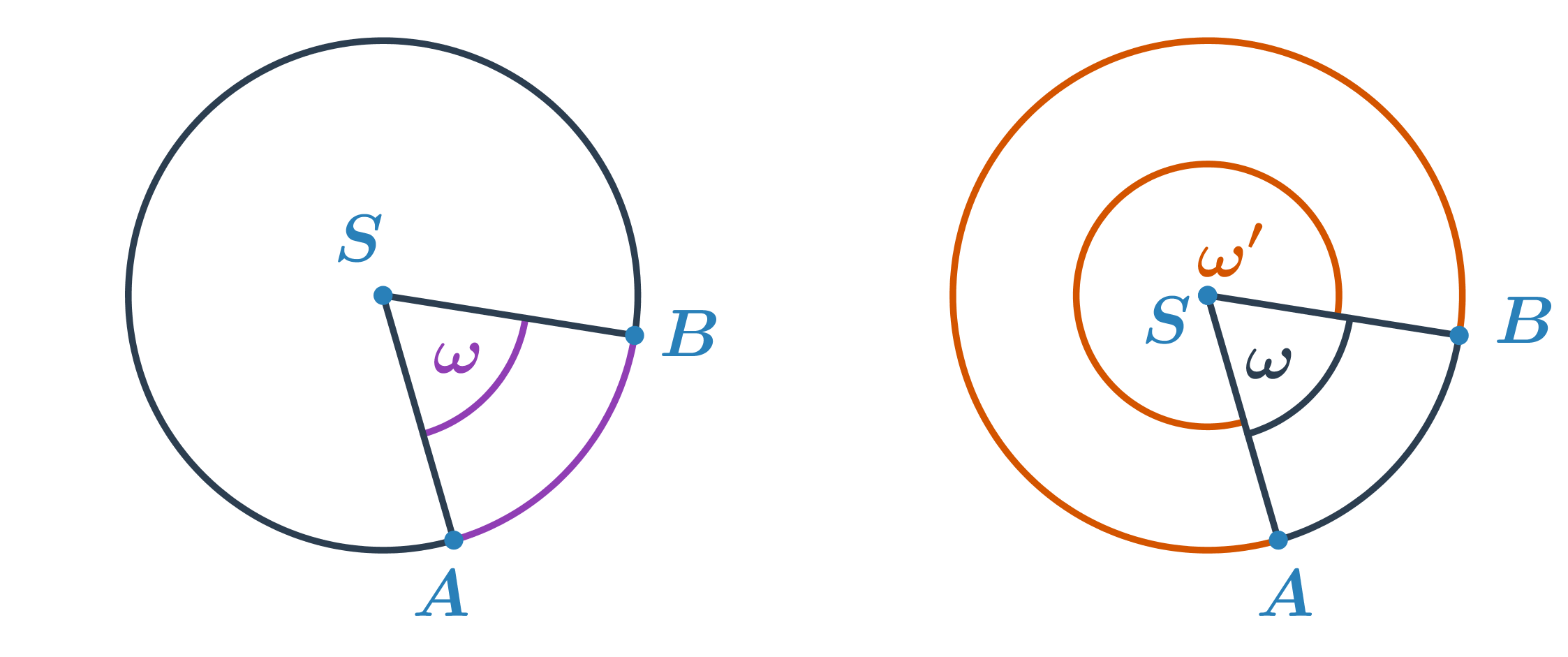
Stredový uhol
- Uhol s vrcholom v strede S kružnice k, ktorého ramená prechádzajú krajnými bodmi A, B oblúka kružnice k.
- Pre každé dva body na kružnici je možné určiť dva stredové uhly. Každý prináleží tomu oblúku, ktorý v danom uhle leží.
Obvodový uhol
- Uhol, ktorého vrchol V leží na kružnici k a jeho ramená prechádzajú bodmi A, B oblúka kružnice k (A \neq V \neq B)
- Všetky obvodové uhly prináležiace oblúku AB s vrcholom V, ktorý na oblúku neleží, majú rovnakú veľkosť.
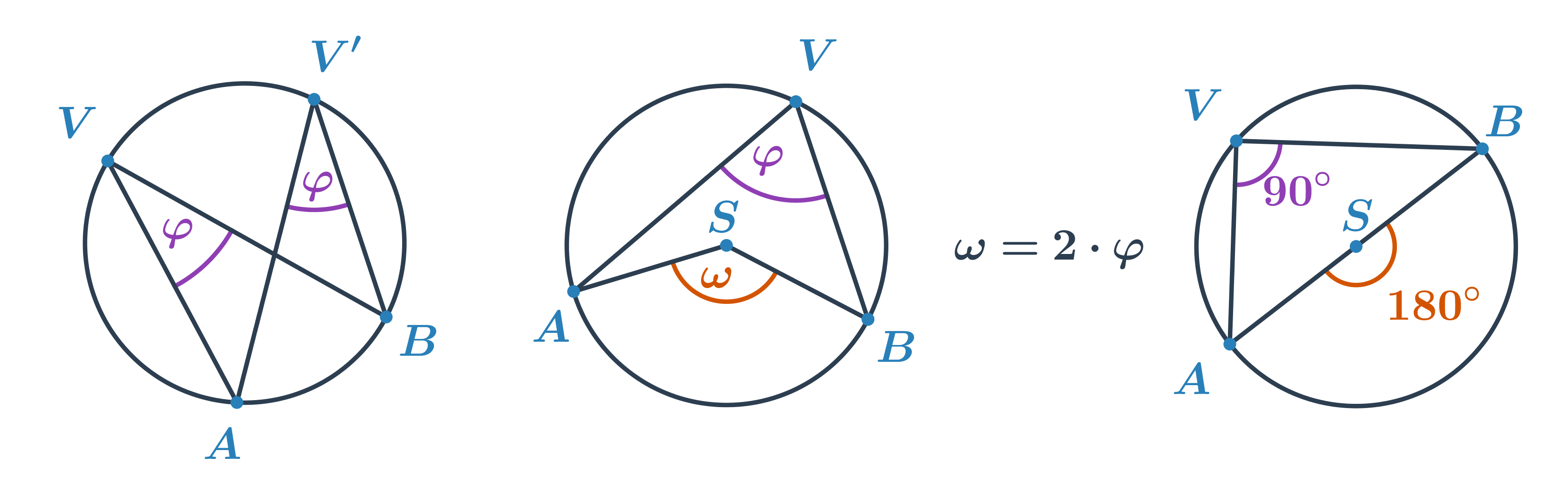
- Veľkosť stredového uhla \omega sa rovná dvojnásobku veľkosti obvodového uhla \varphi príslušného k rovnakému oblúku, \omega = 2\cdot\varphi.
- Tálesova veta: Obvodový uhol nad priemerom kružnice je pravý.
Úsekový uhol
- Uhol, ktorý zviera tetiva AB kružnice k s dotyčnicou t kružnice v bode A alebo B.
- Veľkosť úsekového uhla je rovnaká ako veľkosť obvodového uhla nad oblúkom AB.
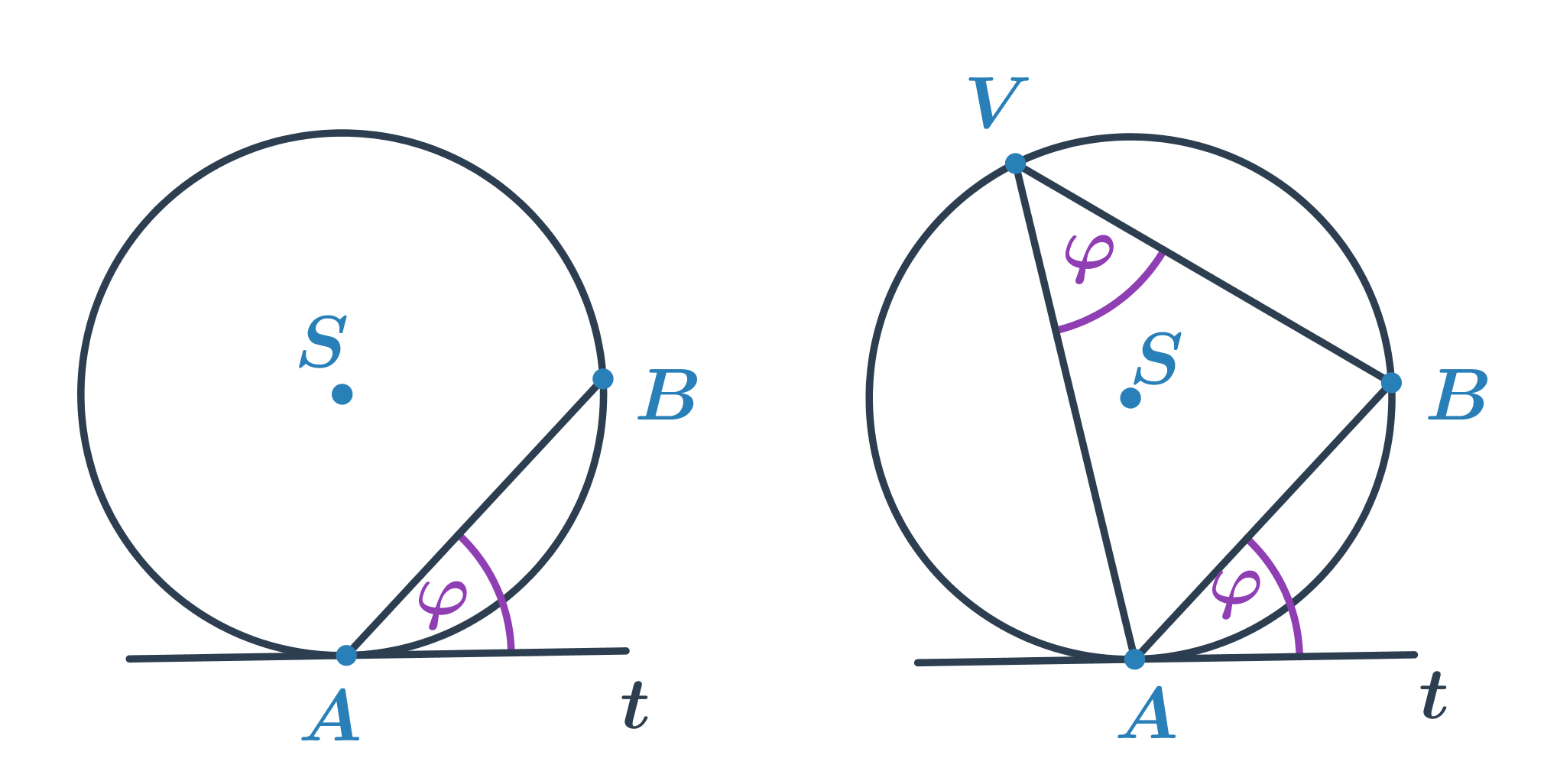
Príklad 1: Určite veľkosť oranžového uhla.
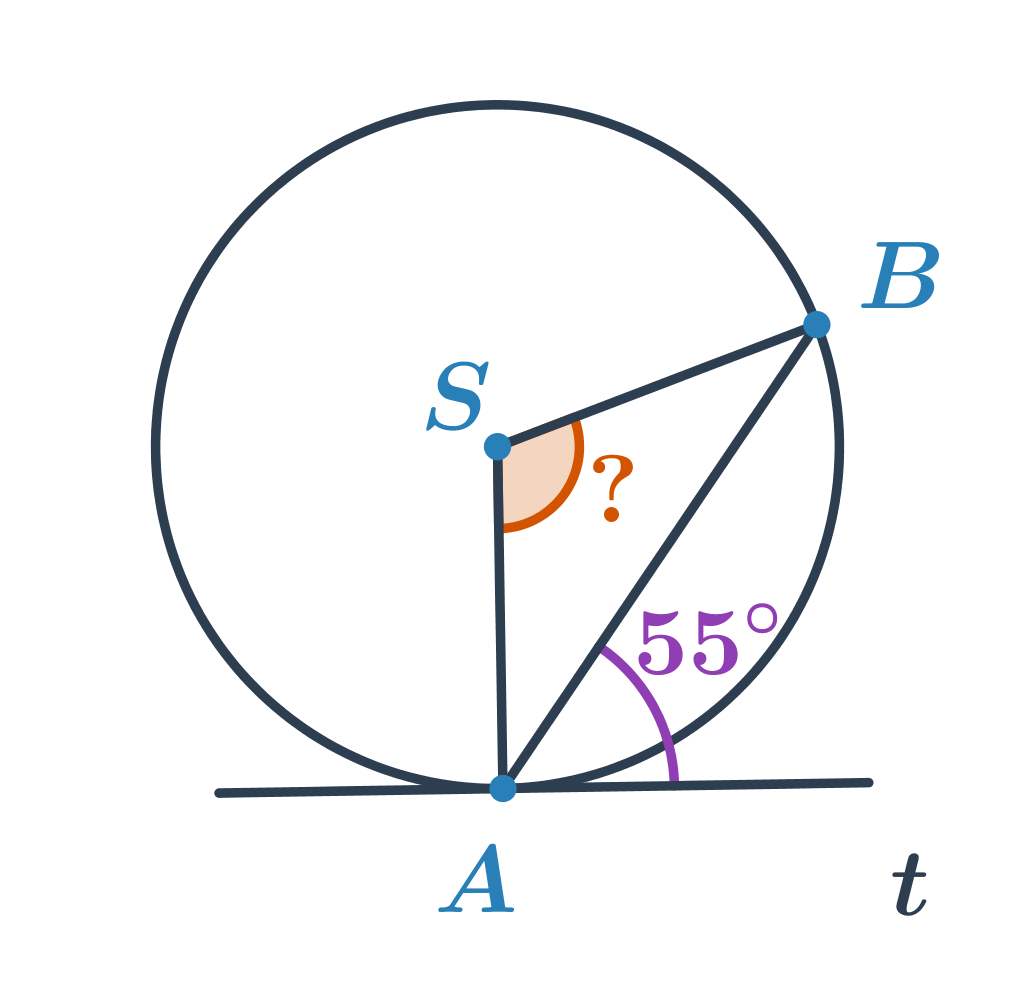
Uhol s veľkosťou 55^\circ je úsekový uhol prináležiaci tetive AB. Vieme, že veľkosti úsekového a príslušného obvodového uhla sú rovnaké, teda 55^\circ. Neznámy uhol je stredový uhol prináležiaci menšiemu oblúku AB. Jeho veľkosť je dvojnásobkom veľkosti obvodového uhla, teda 2\cdot55^\circ=110^\circ.
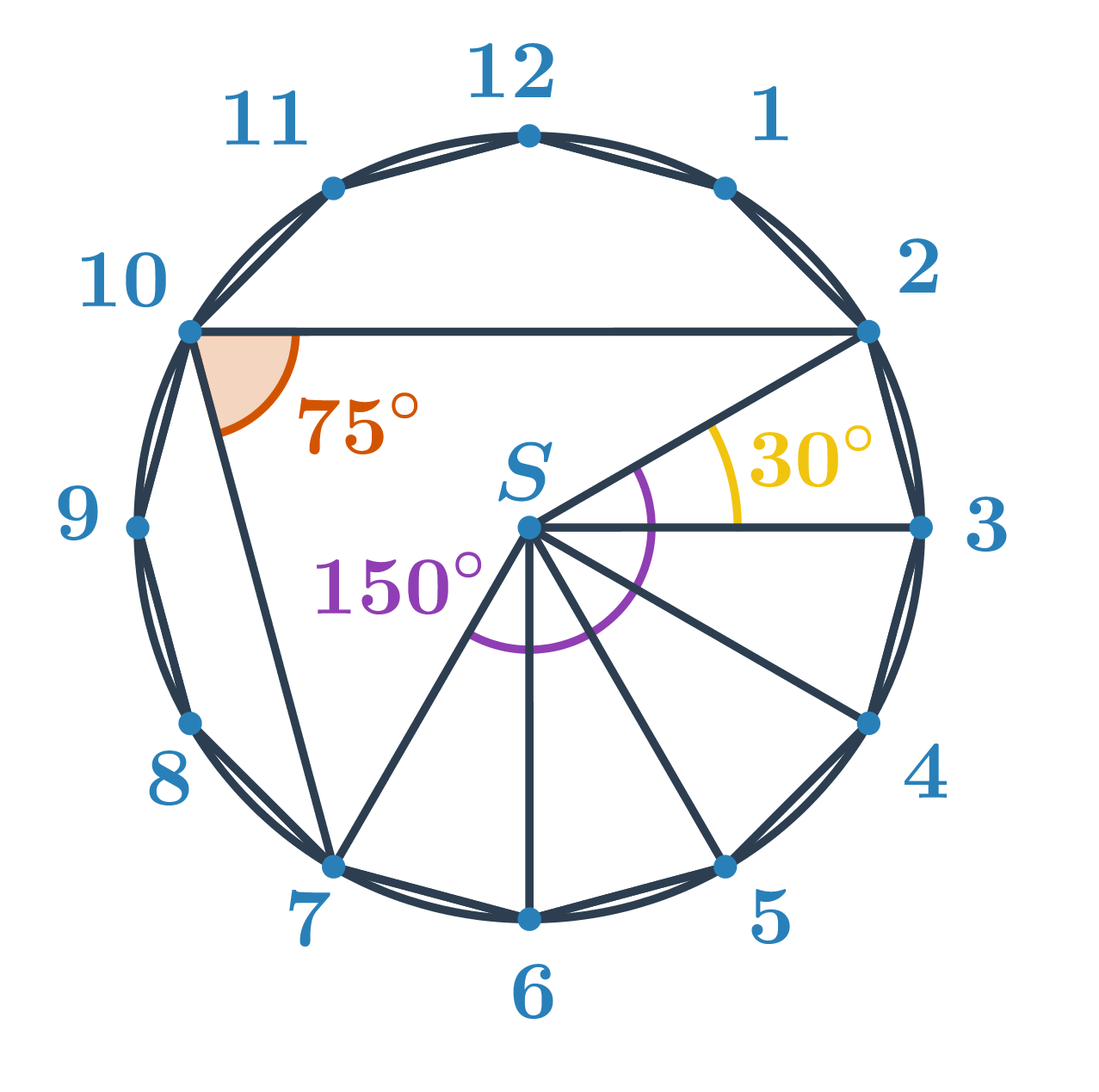
Príklad 2: Určite veľkosť oranžového uhla.
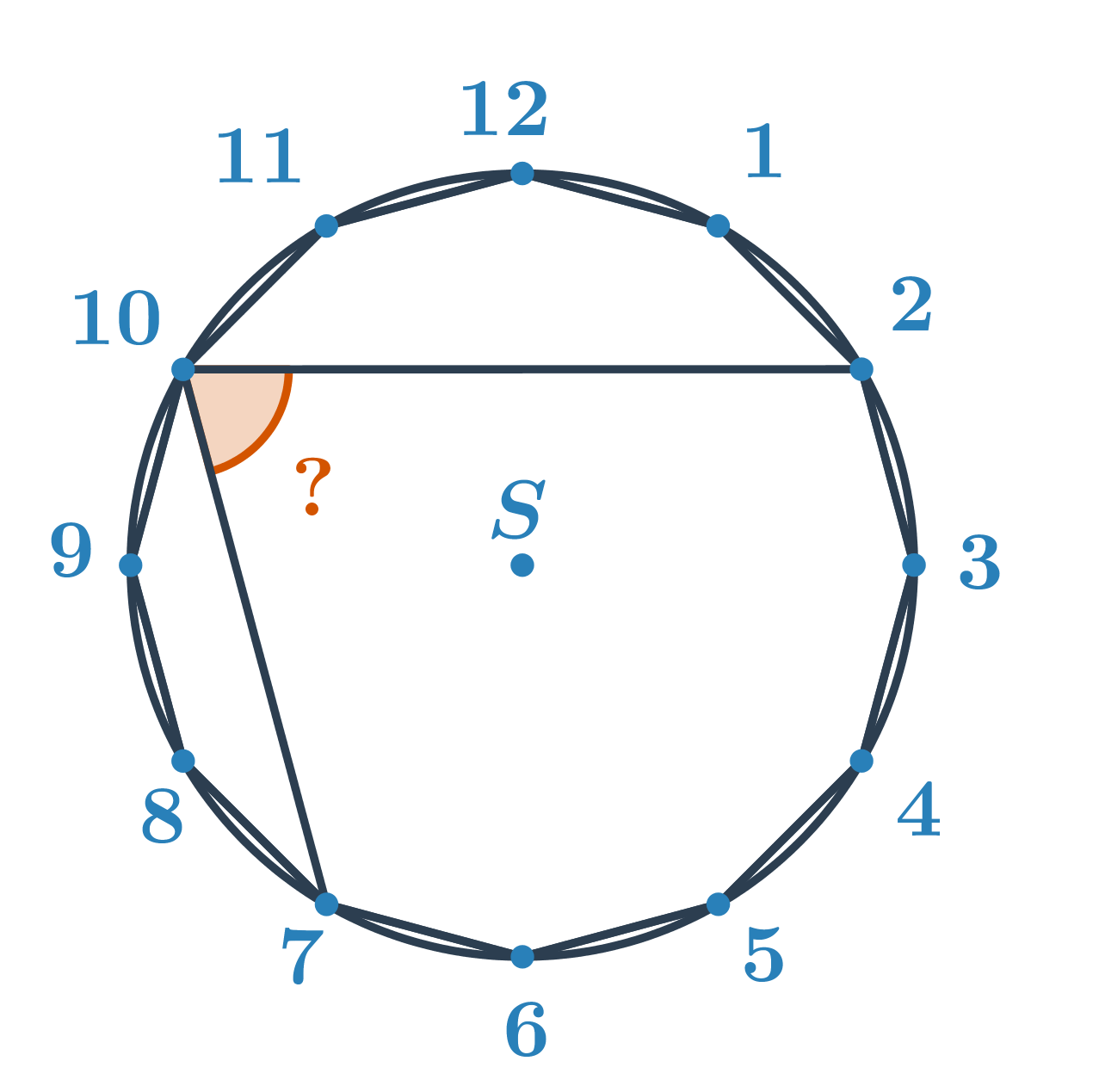
Neznámy uhol je obvodovým uhlom nad menším oblúkom s koncovými bodmi 2 a 7. Určíme veľkosť príslušného stredového uhla. Z kapitoly uhly a mnohouholníky vieme, že veľkosť stredového uhla pravidelného n-uholníka je \frac{360^\circ}{n}. Pre pravidelný dvanásťuholník je teda uhol medzi spojnicami dvoch vedľajších vrcholov a stredu \frac{360^\circ}{12}=30^\circ. Stredový uhol príslušný oblúku 2 a 7 je potom 5\cdot30^\circ=150^\circ. Hľadaný obvodový uhol má polovičnú veľkosť, teda 150^\circ:2=75^\circ.