Uhly a mnohouholníky

Súčet vnútorných uhlov vo všeobecnom mnohouholníku s n stranami (teda n-uholníku) je 180^\circ\cdot(n-2). Napríklad v päťuholníku je súčet vnútorných uhlov 180^\circ(5-2)=540^\circ. Každý vnútorný uhol potom môže mať inú veľkosť.

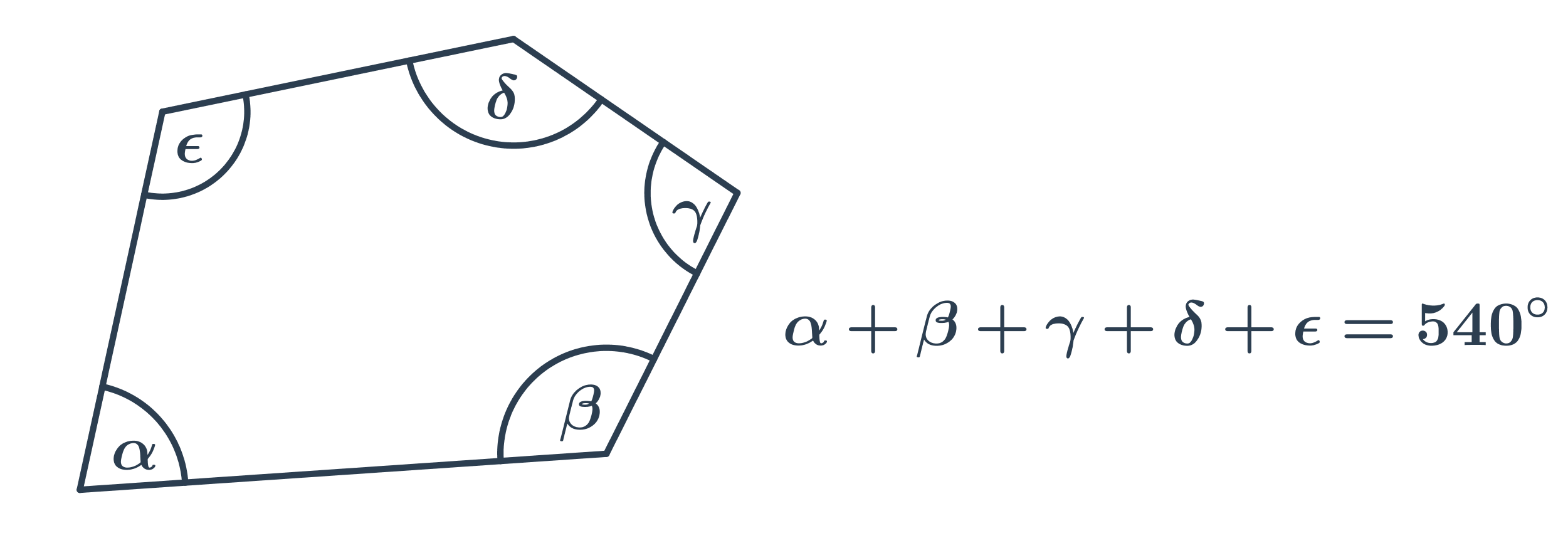
Pravidelné mnohouholníky

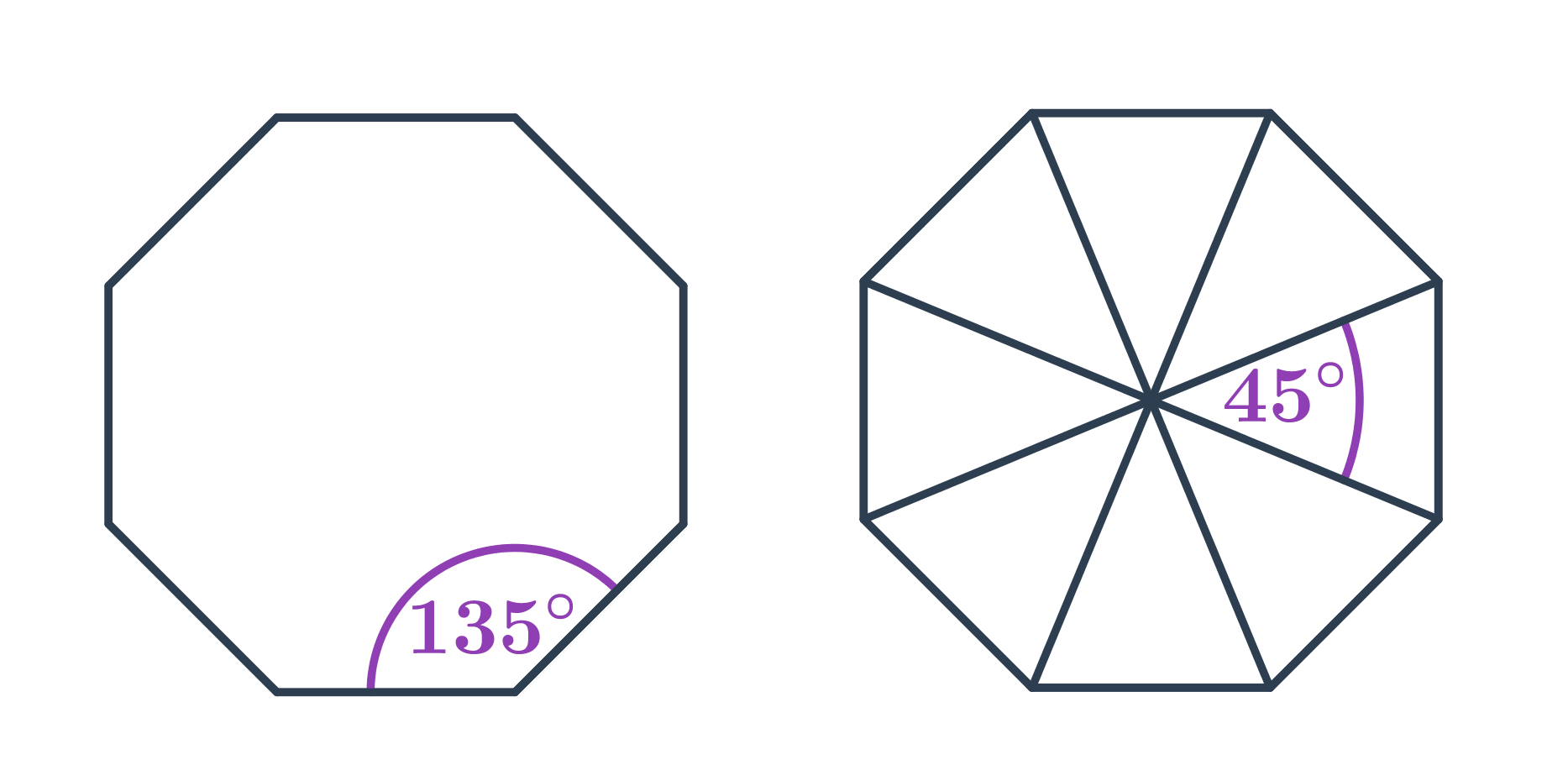
• Každý vnútorný uhol v pravidelnom mnohouholníku s n vrcholmi má veľkosť 180^\circ\cdot\frac{n-2}{n}. Napríklad v pravidelnom osemuholníku má každý vnútorný uhol veľkosť 180^\circ\cdot\frac{8-2}{6}=135^\circ.
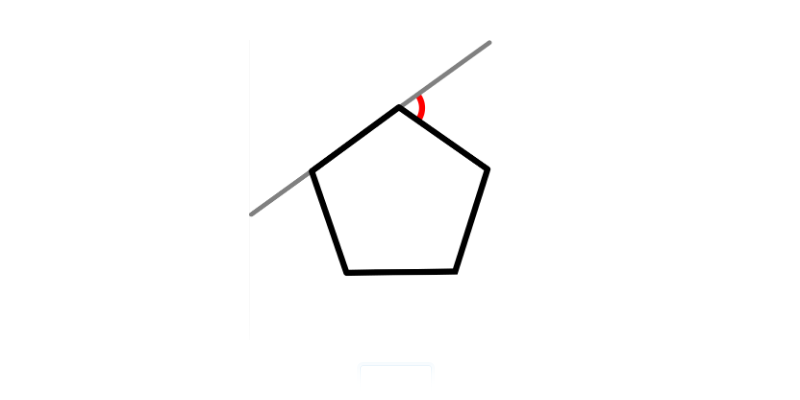
• Veľkosť stredového uhla pravidelného n-uholníka je \frac{360^\circ}{n}. Napríklad v pravidelnom osemuholníku má každý stredový uhol veľkosť \frac{360^\circ}{8}=45^\circ.

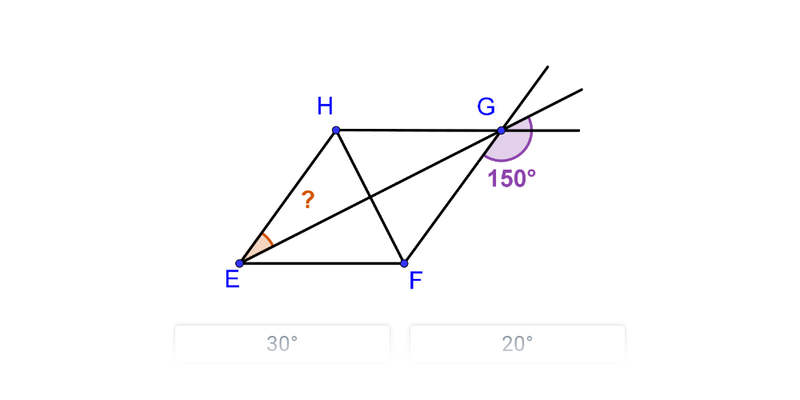
Pri výpočte neznámeho uhla v mnohouholníku je možné využiť aj vrcholových a vedľajších uhlov.

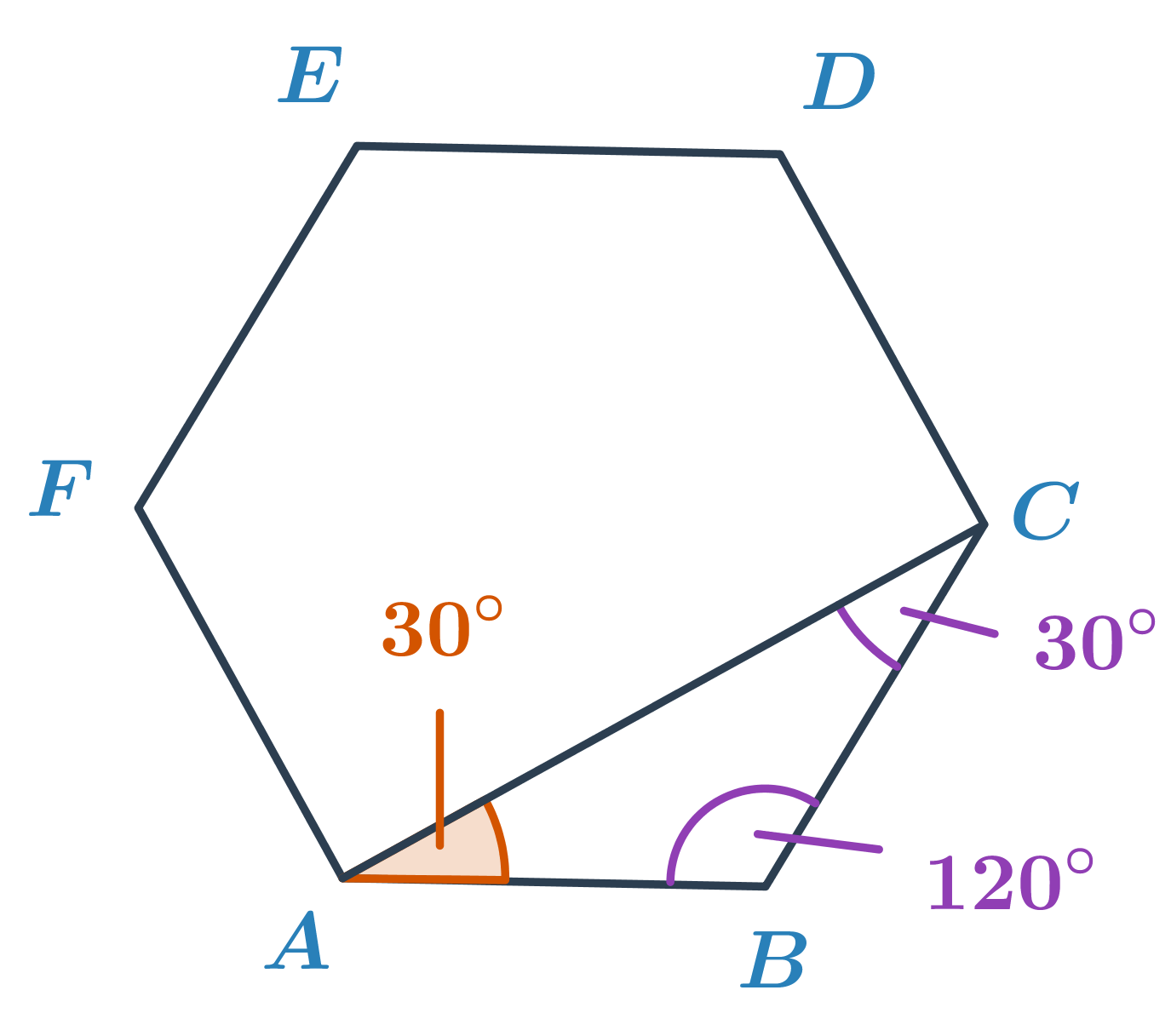
Príklad: Určite veľkosť oranžového uhla v pravidelnom šesťuholníku ABCDEF.

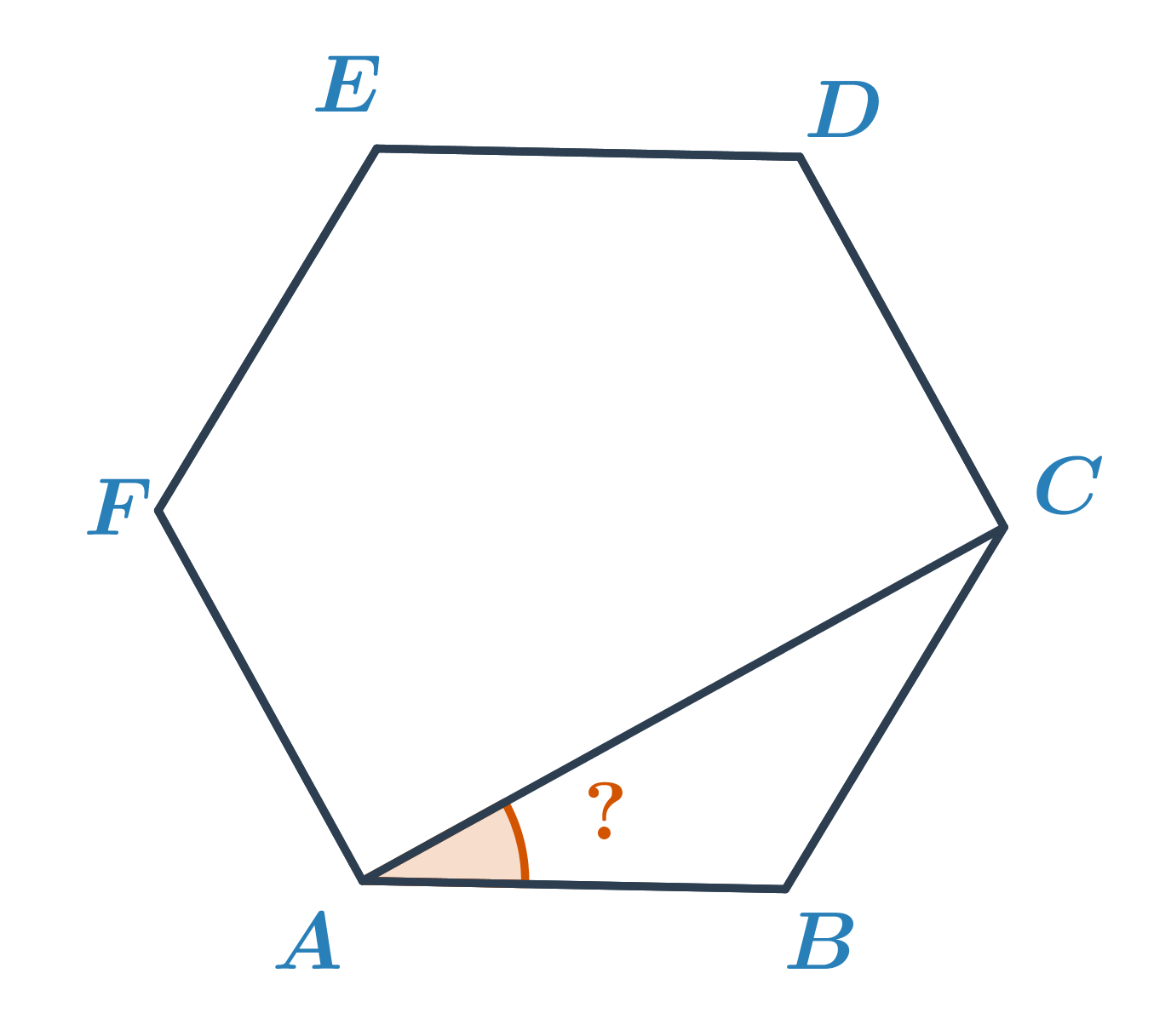
V pravidelnom šesťuholníku má každý uhol rovnakú veľkosť, a to 180^\circ\cdot\frac{6-2}{6}=120^\circ. Uhol ABC má teda veľkosť 120^\circ. Trojuholník ABC je rovnoramenný, uhly pri vrcholoch A a C sú potom zhodné. Ich veľkosť je (180^\circ-120^\circ):2=30^\circ.