Vzorce
Obvod kruhu (aj kružnice) s polomerom r je o=2\pi r. Pre priemer d platí o = \pi d.
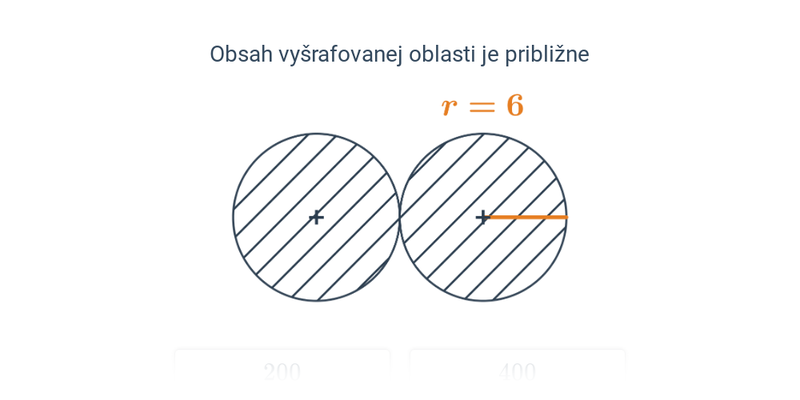
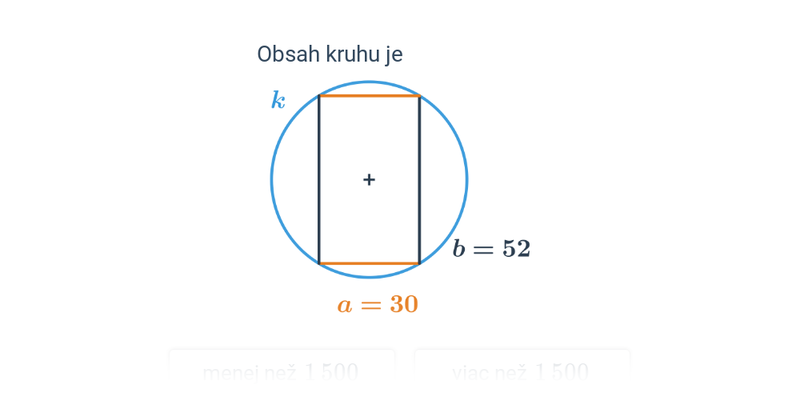
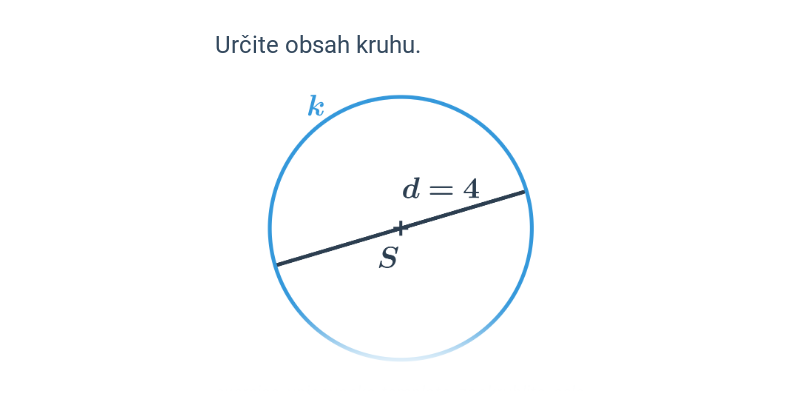
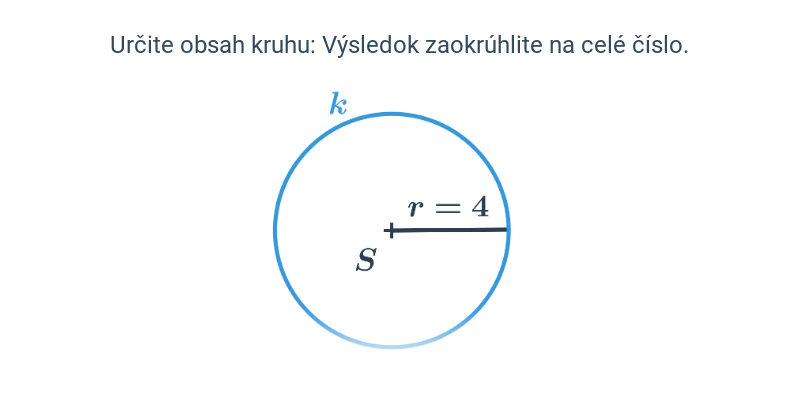
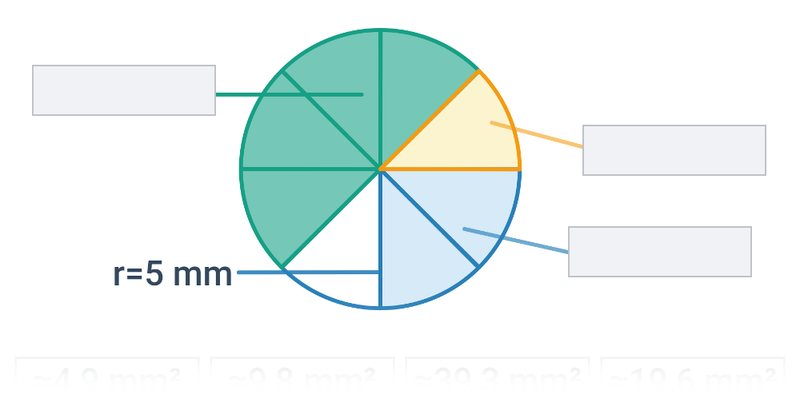
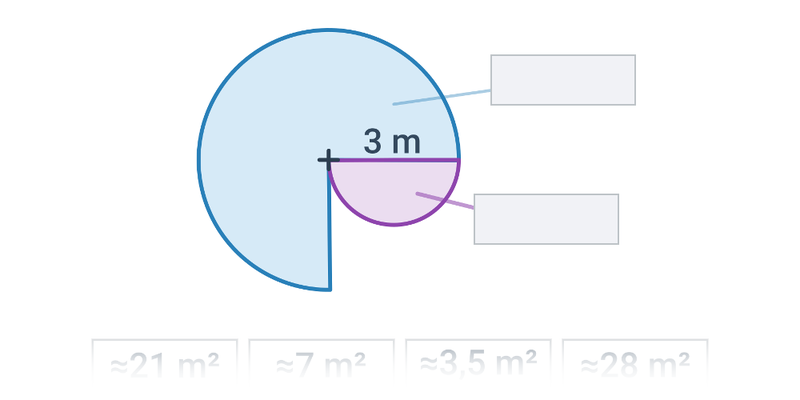
Obsah kruhu s polomerom r je S=\pi r^2. Pre priemer d platí S = \frac{1}{4} \pi d^2.
Konštanta \pi sa nazýva tiež Ludolfovo číslo. \pi je iracionálne číslo, čo znamená, že ho nie je možné vyjadriť zlomkom ani zapísať presne v desiatkovej sústave. Približná hodnota \pi je 3,141 592 65.
Pri výpočte obsahu a obvodu kruhu dávame dobrý pozor na to, či vychádzame zo znalosti polomeru alebo priemeru. Zámena priemeru za polomer je častou chybou.
Intuícia
Základnú intuíciu za vzorcami na výpočet obsahu a obvodu kruhu približuje nižšie uvedený obrázok. Žlté štvorce majú obsah r^2. Oranžový štvorec sa skladá zo štyroch žltých štvorcov, takže má obsah 4\cdot r^2. Kruh má „o trochu menší“ obsah než oranžový štvorec, čo zodpovedá tomu, že obsah kruhu je približne 3{,}14 \cdot r^2. Obvod oranžového štvorca je 8\cdot r. Obvod kruhu je zase „o trochu menší“ – je to 2\pi \cdot r \approx 6{,}3 \cdot r.

Príklady
- Majme kruh s polomerom 3 cm. Jeho obvod je 2\pi \cdot 3 \approx 2 \cdot 3{,}14 \cdot 3 \approx 18{,}8 cm. Jeho obsah je \pi \cdot 3^2 \approx 3{,}14\cdot 9 \approx 28,3 cm².
- Kružnica s priemerom 2 cm má obvod \pi \cdot 2 \approx 6,3 cm. Jej vnútro má obsah \frac{1}{4} \pi \cdot 2^2 = \pi \approx 3,14 cm².
- Stredový kruh na futbalovom ihrisku má polomer 9{,}1 metru. Ak ho chceme obísť po jeho okrajovej čiare, prejdeme 2 \pi \cdot 9{,}1 \approx 57 metrov. Ak by sme chceli všetku trávu v kruhu nafarbiť na ružovo, museli by sme nafarbiť \pi \cdot 9{,}1^2 \approx 260 m² trávy.
Presúvanie
Presúvanie kartičiek na správne miesto. Jednoduché ovládanie, zaujímavé a neotrepané úlohy.

Obsah kruhu (stredné)
Zadaní: 16
Typicky zaberie: 10 min

Obsah kruhu (ťažké)
Zadaní: 16
Typicky zaberie: 12 min


 Slovenčina
Slovenčina Angličtina
Angličtina Informatika
Informatika Vieme to
Vieme to Nemčina
Nemčina Biológia
Biológia Zemepis
Zemepis Chémia
Chémia Fyzika
Fyzika