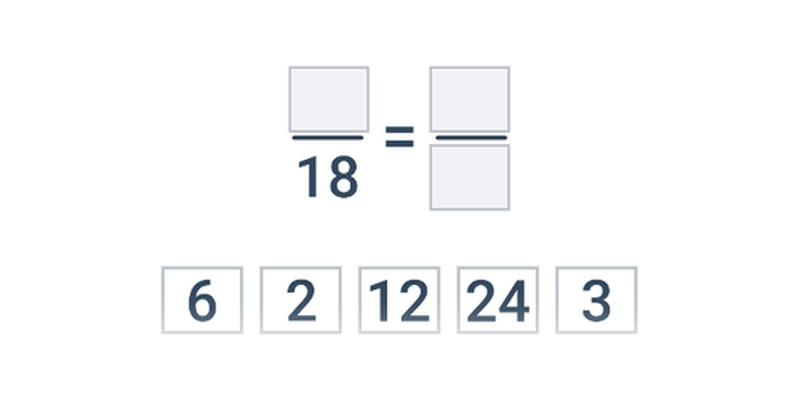
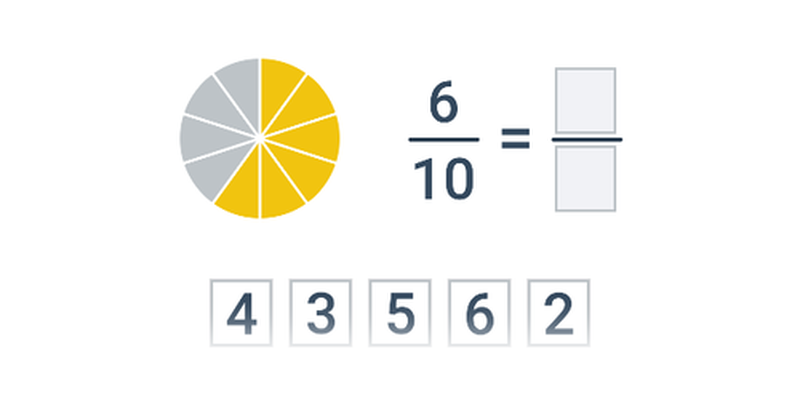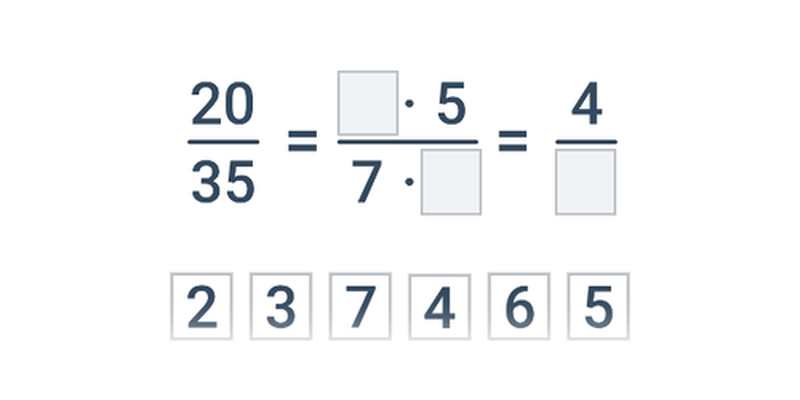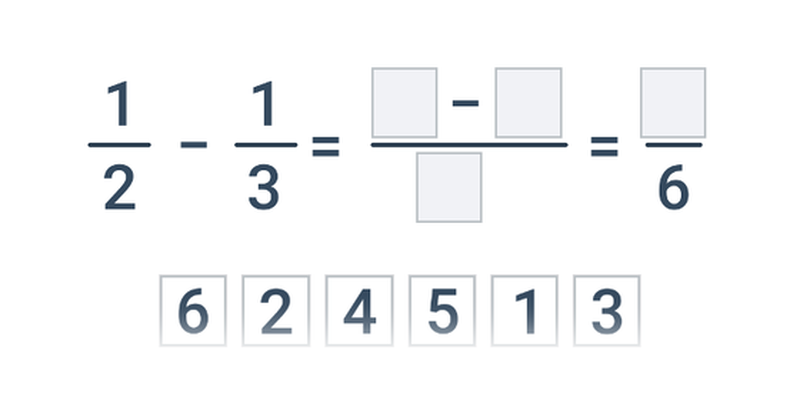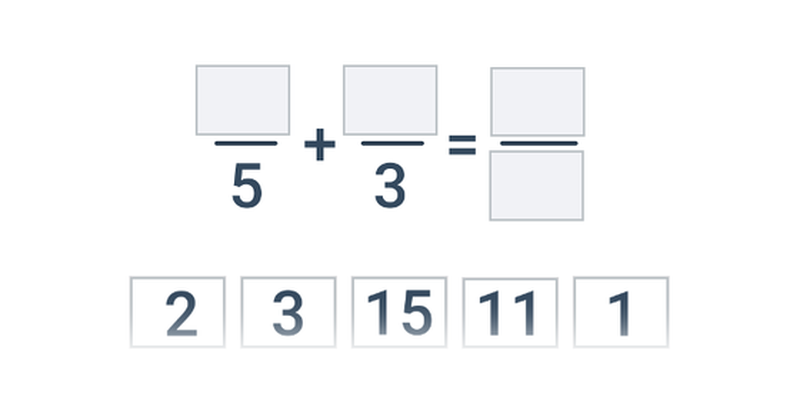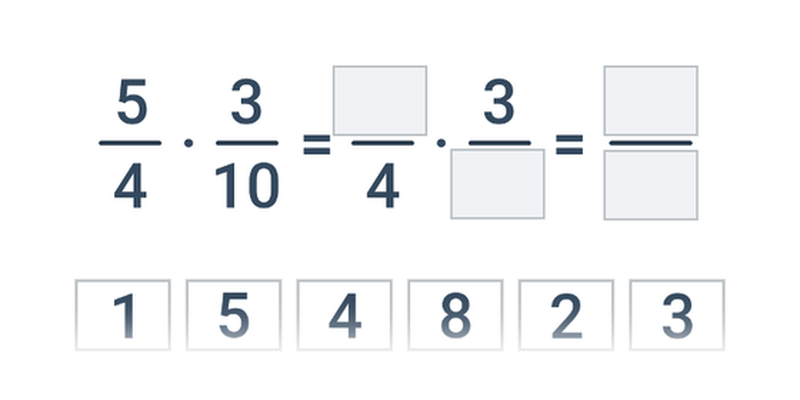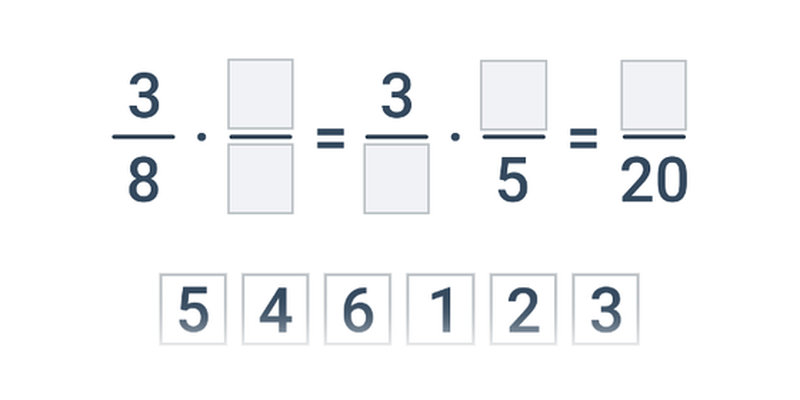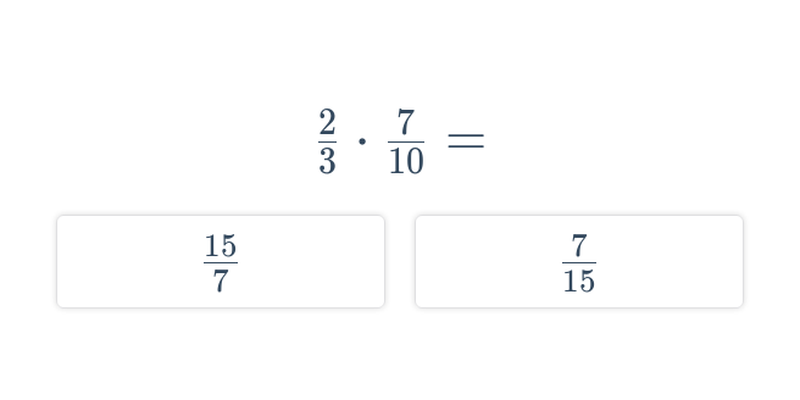Základné výpočty so zlomkami sú nasledujúce:
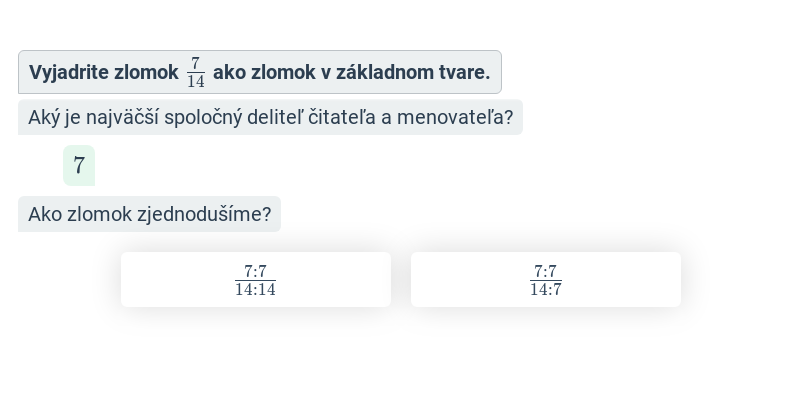
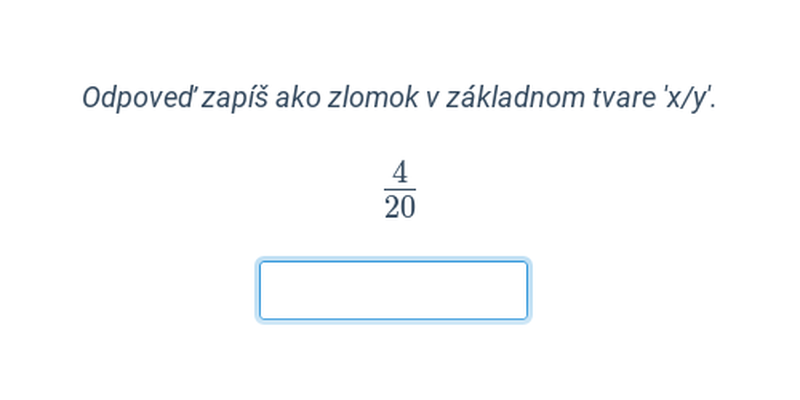
- Zlomky sa krátia tak, že čitateľ aj menovateľ vydelíme ich spoločným deliteľom.
- Zlomok \frac{9}{12} môžeme skrátiť na \frac{3}{4}, pretože čitateľ aj menovateľ majú spoločný deliteľ 3.
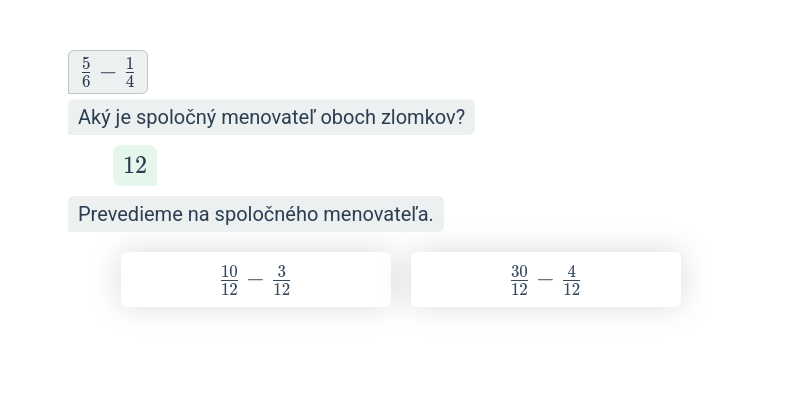
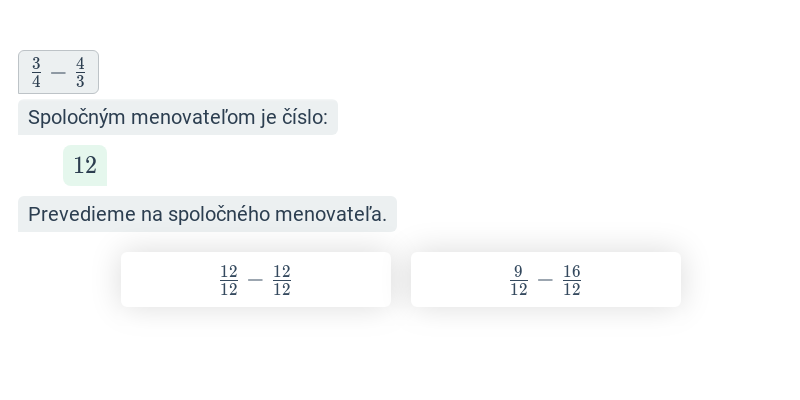
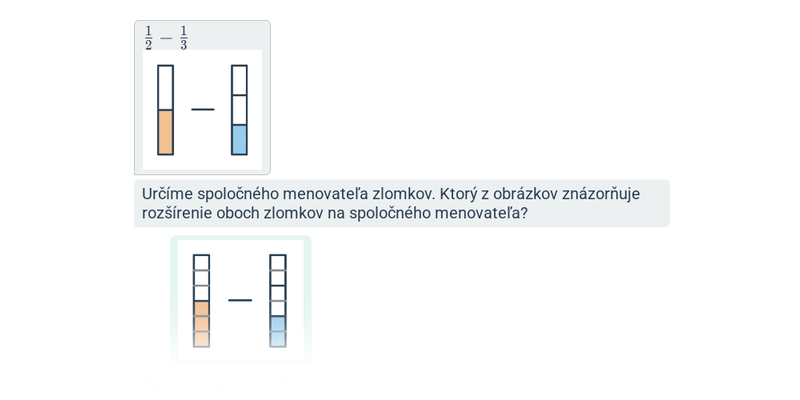
- Pre sčítanie a odčítanie zlomkov je nutné previesť zlomky na spoločný menovateľ.
- \frac{1}{4} + \frac{1}{6} prevedieme na spoločný menovateľ 12 a dostaneme \frac{3}{12} + \frac{2}{12} = \frac{5}{12}.
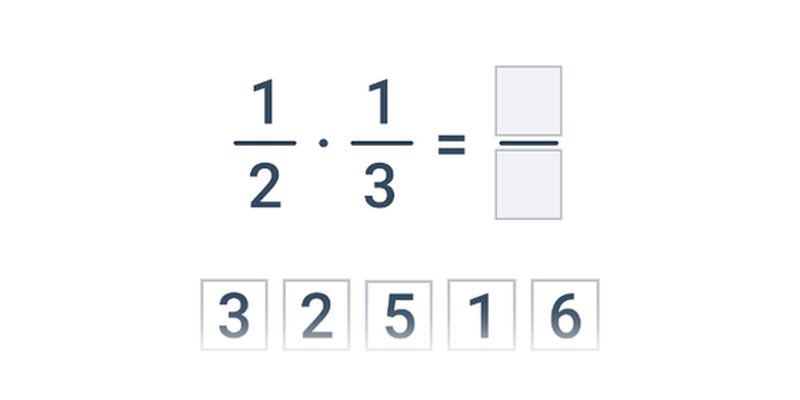
- Násobenie sa vykonáva tak, že vynásobíme čitateľ aj menovateľ medzi sebou.
- \frac{2}{3} \cdot \frac{3}{4} = \frac{6}{12} = \frac{1}{2}
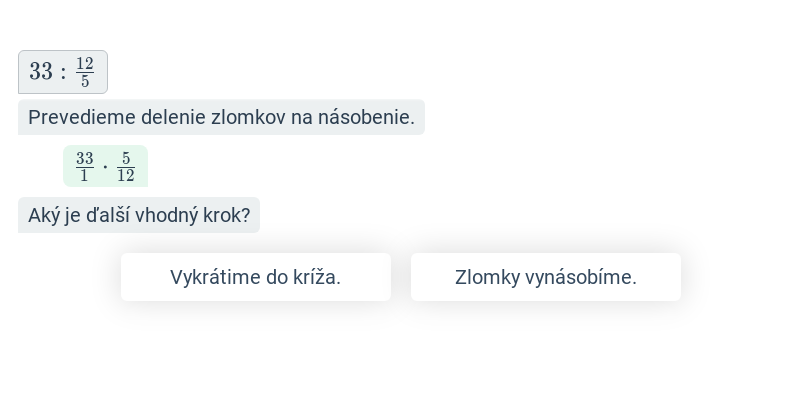
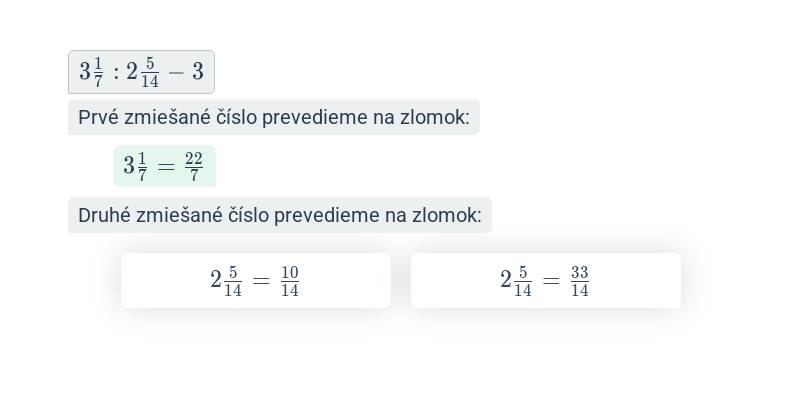
- Delenie sa vykonáva násobením prevráteného zlomku.
- \frac{2}{3} : \frac{3}{4} = \frac{2}{3} \cdot \frac{4}{3} = \frac{8}{9}
- Prevod zlomku na percentá sa vykonáva pomocou násobenia 100.
- \frac{3}{4} = 0{,}75 = 75 \%
- Zlomky prevedieme na desatinné čísla tak, že čitateľ vydelíme menovateľom. Naopak desatinné číslo je možné previesť na zlomok pomocou roznásobenie mocninami desiatky.
- \frac{2}{5} = 2 : 5 = 0{,}4
- 0{,}25 = 0{,}25 \cdot\frac{100}{100} = \frac{25}{100}, čo po skrátení dáva \frac{1}{4}
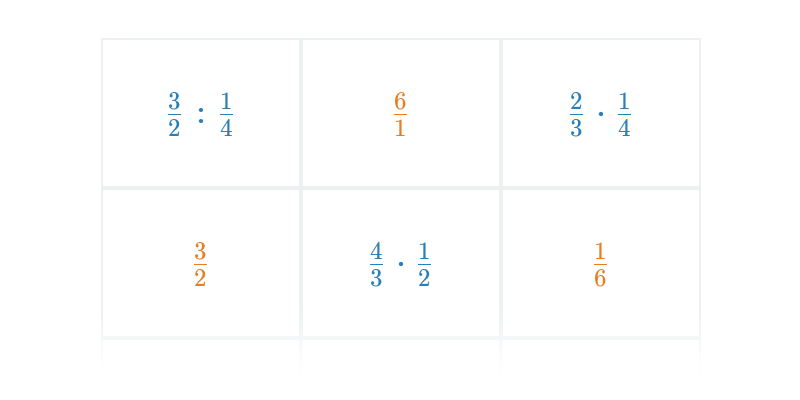
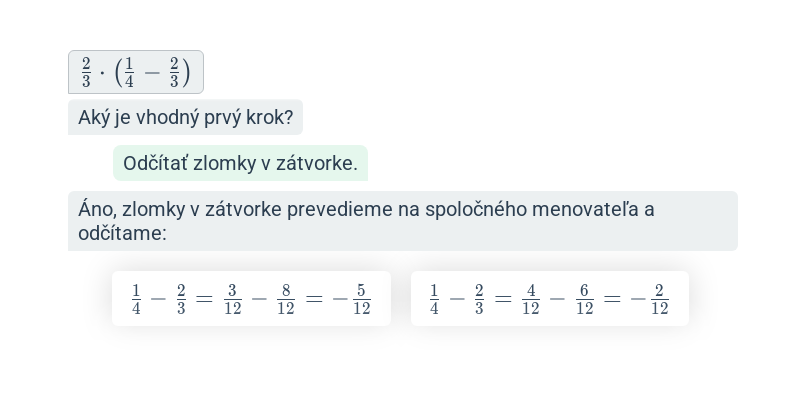
Kombinácie operácií so zlomkami
- Zadania kombinujúce rôzne aritmetické operácie so zlomkami.
Presúvanie
Presúvanie kartičiek na správne miesto. Jednoduché ovládanie, zaujímavé a neotrepané úlohy.
Výpočty so zlomkami
Rozhodovačka
Rýchle precvičovanie výberom z dvoch možností.
Výpočty so zlomkami
Výpočty so zlomkami: mix
Pexeso
Hľadanie dvojíc, ktoré k sebe patria.
Výpočty so zlomkami
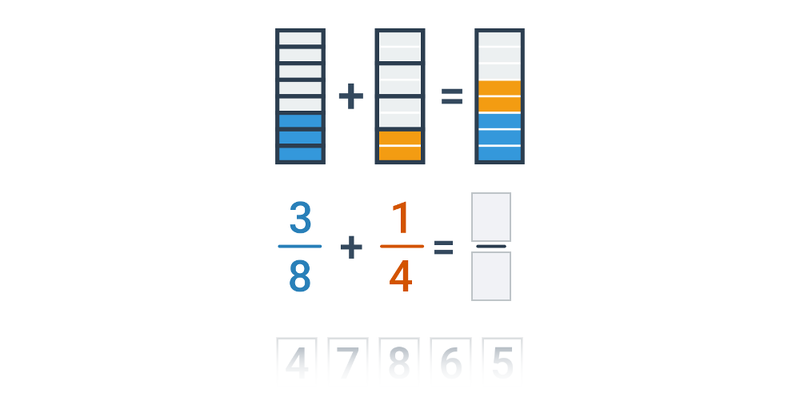
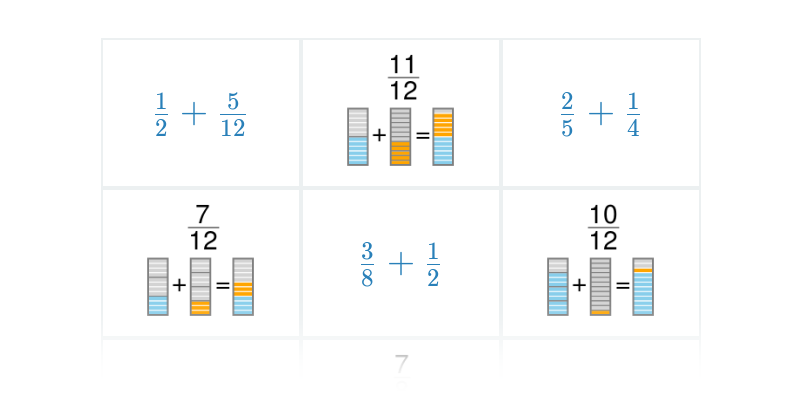
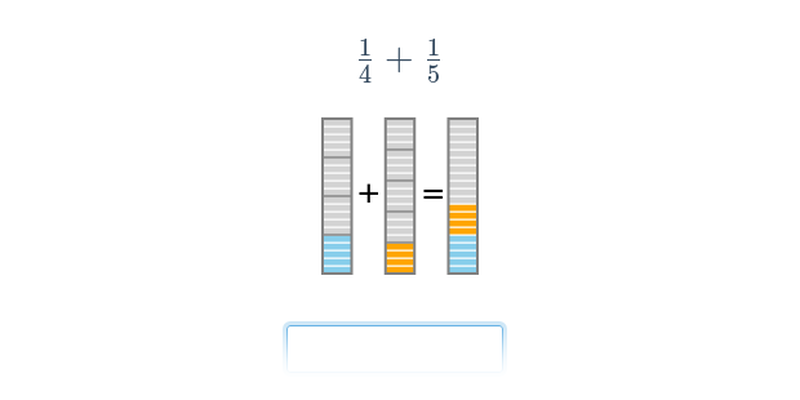
Zlomky: sčítanie obrázkami
Krok za krokom
Doplňovanie jednotlivých krokov v rozsiahlejšom postupe.
Výpočty so zlomkami
Sčítanie a odčítanie zlomkov s obrázkami
Kombinácie operácií so zlomkami
Počítanie
Cvičenie, v ktorom píšete odpoveď na klávesnici.
Výpočty so zlomkami
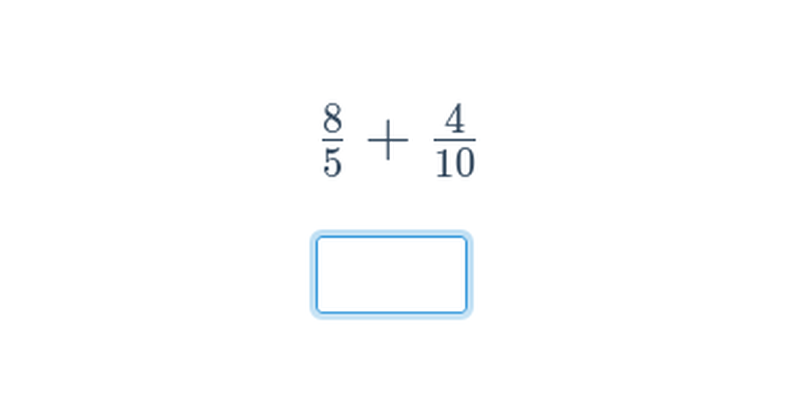
Sčítanie zlomkov s obrázkami
Sčítanie zlomkov s celočíselným výsledkom
Výpočty so zlomkami: mix
Slovné úlohy
Klasické precvičovanie slovných úloh s pestrou ponukou zadaní a vysvetľujúcimi textami.
Výpočty so zlomkami
Výpočty so zlomkami: mix