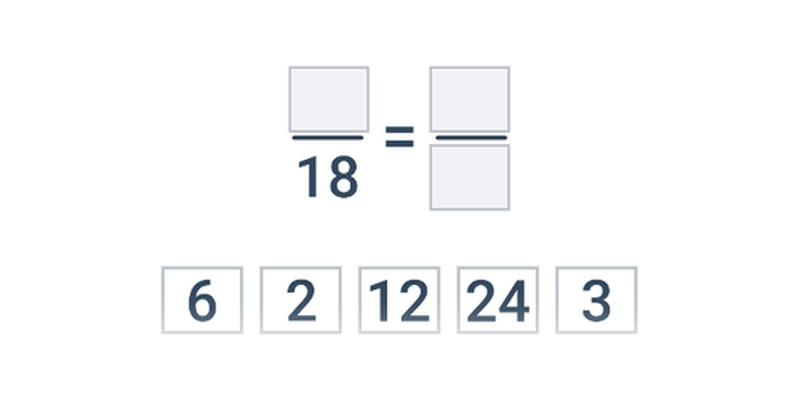
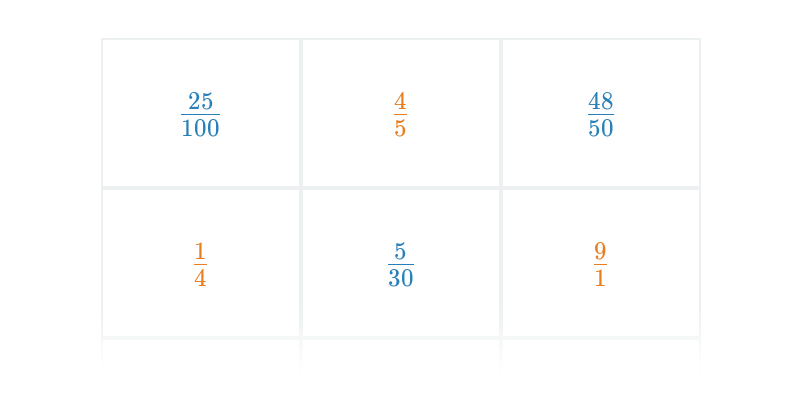
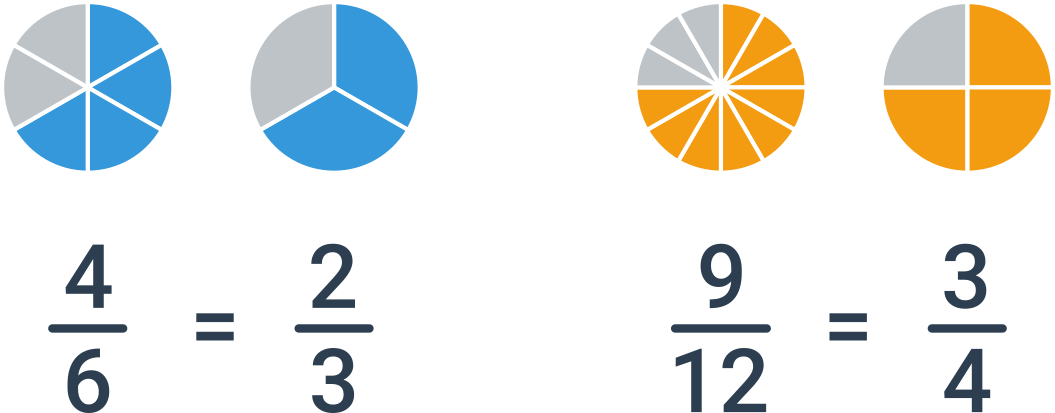
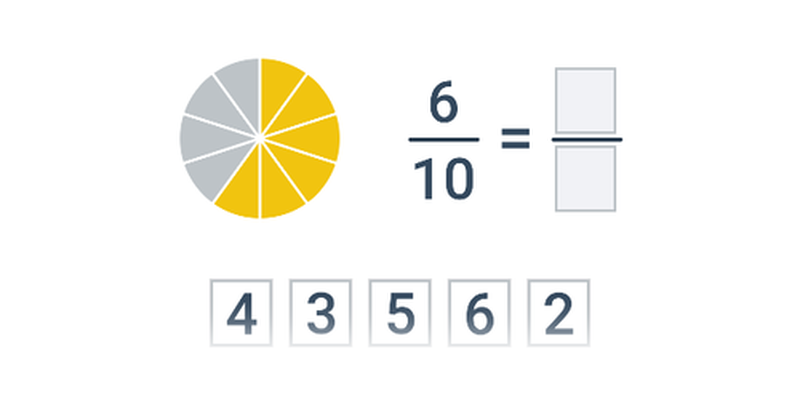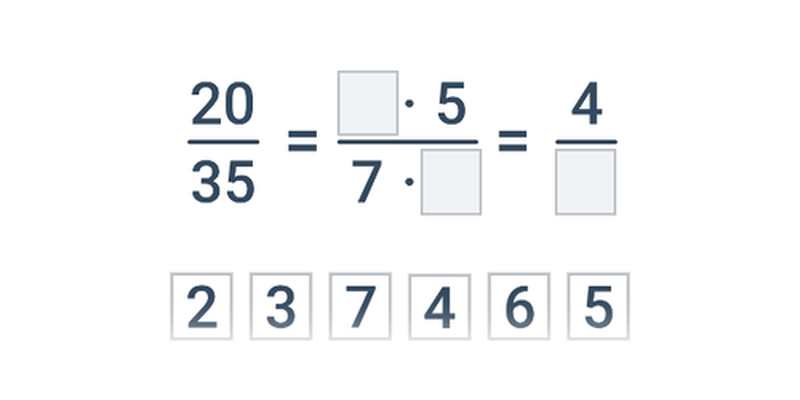Rovnakú hodnotu môžeme vyjadriť mnohými zlomkami, napríklad \frac23 = \frac46 = \frac{10}{15} = \frac{200}{300}. Len jedno možné vyjadrenie však považujeme za základný tvar. Zlomok je v základnom tvare, ak sú čitateľ a menovateľ nesúdeliteľné, nemajú teda žiadny spoločný deliteľ okrem jednotky. V uvedenom príklade je v základnom tvare zlomok \frac23.
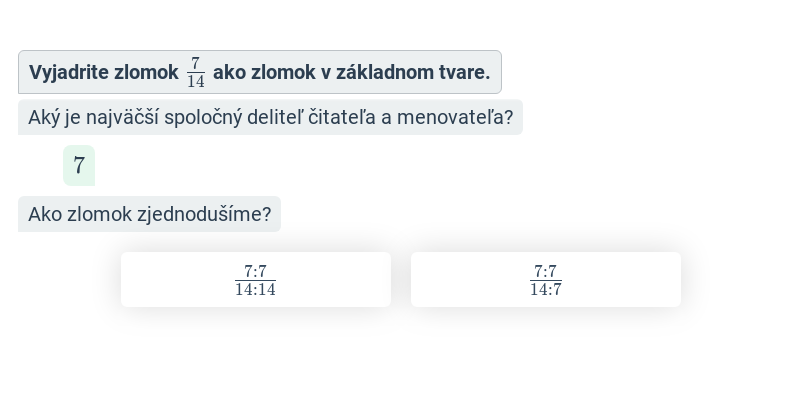
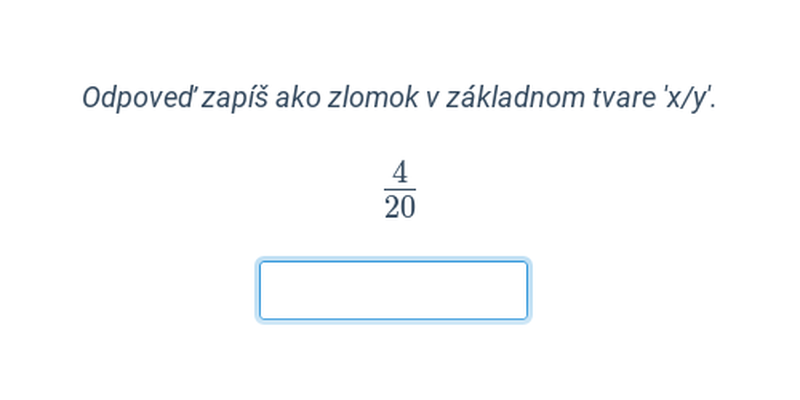
Ako krátenie zlomku sa označuje operácia, kedy čitateľ a menovateľ vydelíme rovnakým, nenulovým číslom. Krátenie zachováva hodnotu zlomku. Ak chceme zlomok previesť do základného tvaru, krátime najväčším spoločným deliteľom čitateľa a menovateľa.
Príklady
Zlomok \frac{15}{28} je v základnom tvare, pretože čísla 15 a 28 nemajú spoločný deliteľ (sú nesúdeliteľné).
Zlomok \frac{25}{30} môžeme krátiť číslom 5, čím dostaneme zlomok \frac{5}{6}, ktorý je v základnom tvare.
Zlomok \frac{12}{18} môžeme krátiť číslom 2, čím dostaneme zlomok \frac{6}{9}. Ak chceme krátiť na základný tvar, nájdeme najväčší spoločný deliteľ čísel 12 a 18, čo je 6. Po krátení číslom 6 dostávame zlomok \frac{2}{3}.
Presúvanie
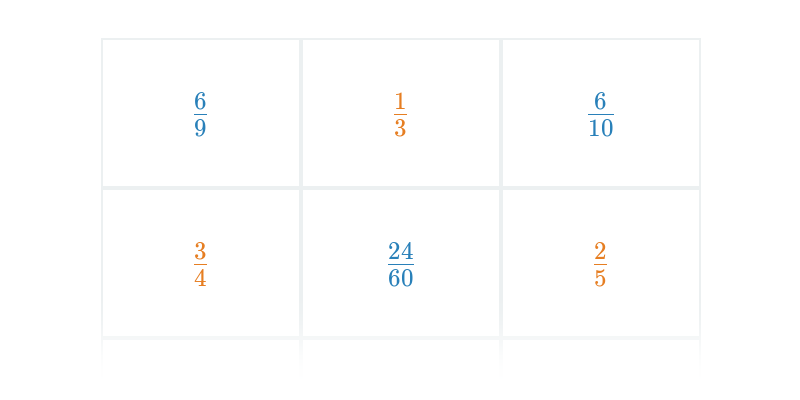
Presúvanie kartičiek na správne miesto. Jednoduché ovládanie, zaujímavé a neotrepané úlohy.
Krok za krokom
Doplňovanie jednotlivých krokov v rozsiahlejšom postupe.