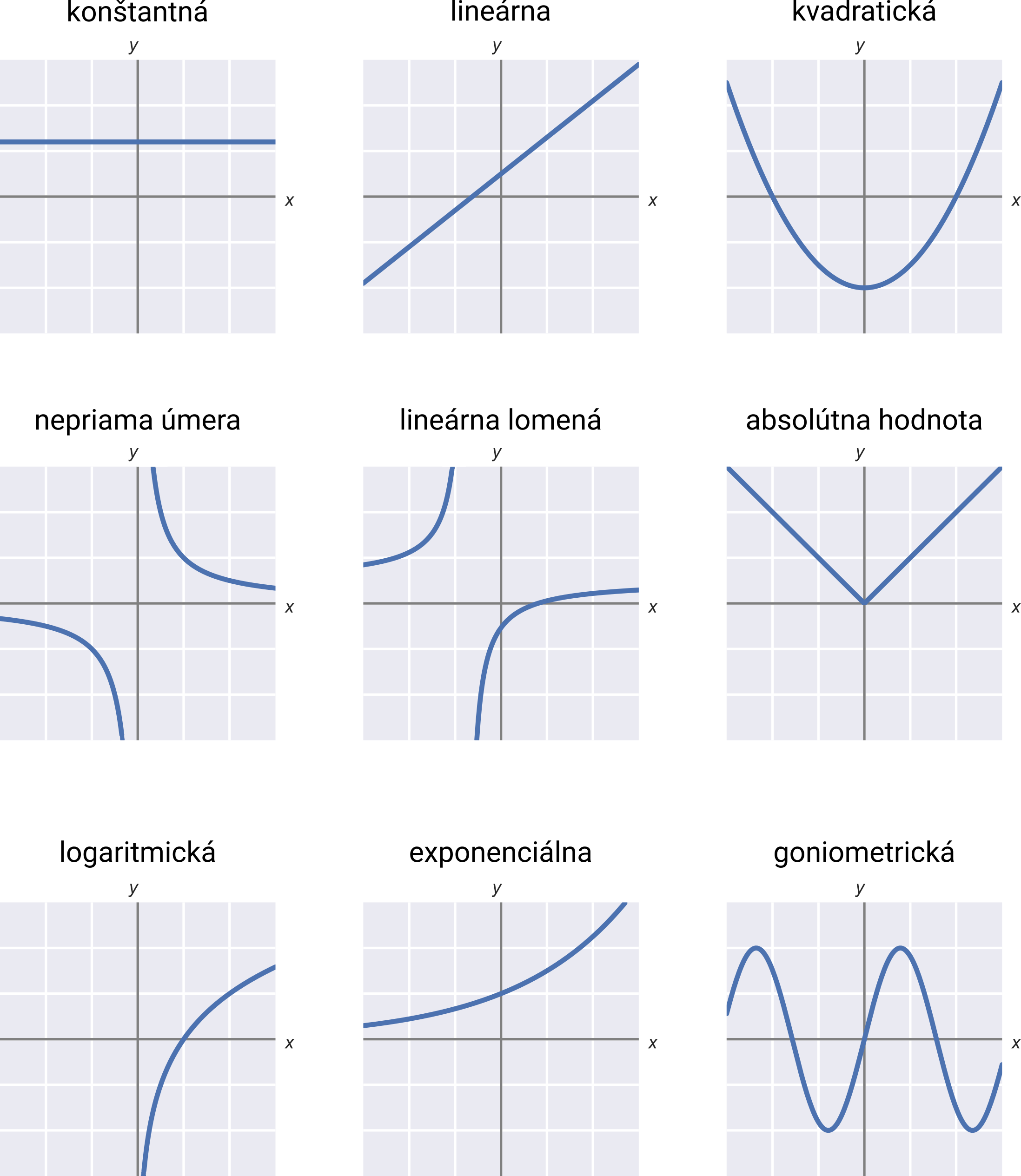
Výpis prehľadov
Funkcie
Podkapitoly
- Funkcie
- Základné typy funkcií
- Vlastnosti funkcií
- Grafy funkcií
- Grafy lineárnych funkcií
- Grafy kvadratických funkcií
- Grafy funkcií s absolútnou hodnotou
- Grafy lineárnych lomených funkcií
- Grafy mocninových funkcií
- Grafy goniometrických funkcií
- Grafy exponenciálnych funkcií
- Grafy logaritmických funkcií
- Grafy lineárnych nerovníc
- Lineárne funkcie
- Vlastnosti lineárnej funkcie
- Lineárne lomené funkcie
- Vlastnosti lineárnej lomenej funkcie
- Kvadratické funkcie
- Vlastnosti kvadratickej funkcie
- Goniometrické funkcie
- Goniometrické funkcie a pravouhlý trojuholník
- Hodnoty goniometrických funkcií
- Goniometrické funkcie: vzťahy a vzorce
- Vlastnosti goniometrických funkcií
- Mocninové funkcie
- Exponenciálne funkcie
- Vlastnosti exponenciálnych funkcií
- Logaritmické funkcie
- Vlastnosti logaritmických funkcií
Funkcia je matematický vzťah, ktorý priraďuje každému vstupu práve jeden výstup. Ako intuitívny príklad funkcie môže poslúžiť „zafarbovač na modro“ – na vstup berie kocku, na výstup dáva kocku zafarbenú na modro. Také poňatie funkcií nájdeme tiež v informatike, kde funkcie pomáhajú definovať rôzne operácie a algoritmy. V matematike väčšinou pracujeme s funkciami nad číslami, kde vzťah medzi vstupom a výstupom popisuje matematický výraz.
Medzi základné typy funkcií, s ktorými sa v matematike stretávame, patria:
| Typ | Príklad |
|---|---|
| Lineárne funkcie | f(x) = 3x + 1 |
| Kvadratické funkcie | f(x) = x^2 - 4x + 3 |
| Goniometrické funkcie | f(x) = \sin(x) |
| Exponenciálne a logaritmické funkcie | f(x) = 2^x |
Téma typy a vlastnosti funkcí sa zaoberá podrobnejším rozlišovaním medzi jednotlivými typmi funkcií a ich vlastnosťami, ako sú periodičnosť alebo ohraničenosť.
Funkcie pre lepšie pochopení často zakresľujeme graficky, čo nám umožňuje lepšie vidieť vzťah medzi vstupom a výstupom. Téma grafy funkcií zastrešuje precvičovanie v tomto stvárnení.
HoreVlastnosti funkcií
Pozn. V rámci zjednodušenia popisu berieme do úvahy len funkcie, ktorých definičný obor tvoria všetky reálne čísla.
Funkcia f sa nazýva párna práve vtedy, keď je pre každé x f(-x) = f(x). Graf párnej funkcie je súmerný podľa osi y. Príklady párnych funkcií: f_1(x) = x^2, f_2(x) = \cos(x), f_3(x) = x^4-3x^2+2.
Funkcia f sa nazýva nepárna práve vtedy, keď je pre každé x f(-x) = -f(x). Graf nepárnej funkcie je súmerný počiatku. Príklady nepárnych funkcií: f_1(x) = 3x, f_2(x) = \sin(x), f_3(x) = x^3-2x.
Funkcia f sa nazýva periodická práve vtedy, keď existuje číslo p != 0 (perióda funkcie) také, že pre každé x platí f(x+p)=f(x). Typickými príkladmi periodických funkcií sú funkcie goniometrické. Naopak napríklad polynómy periodické nie sú (s výnimkou konštantnej funkcie).
Funkcia f sa nazýva zdola ohraničená práve vtedy, keď existuje také číslo k, že pre každé x platí f(x) \geq k. Funkcia f sa nazýva zhora ohraničená, práve keď existuje také číslo k, že pre každé x platí f(x) \leq k. Funkcia f sa nazýva ohraničená, keď je súčasne ohraničená zhora aj zdola. Príklady:
- Funkcia f(x) = \sin(x) je ohraničená.
- Funkcia f(x) = x^2 je ohraničená zdola (pretože \forall x: f(x) \geq 0), ale nie je ohraničená zhora.
- Funkcia f(x) = 2x nie je ohraničená ani zhora, ani zdola.
Funkcia f sa nazýva prostá práve vtedy, keď pre každú dvojicu x_1 \neq x_2 platí f(x_1) \neq f(x_2).
Funkcia f sa nazýva rastúca práve vtedy, keď pre každú dvojicu x_1 \lt x_2 platí f(x_1) \lt f(x_2).
Funkcia f se nazýva klesajúca práve vtedy, keď pre každú dvojicu x_1 > x_2 platí f(x_1) > f(x_2).
HoreGrafy funkcií
Graf funkcie f zadanej predpisom y=f(x) pre všetky x z množiny D(f) je množina bodov v rovine, ktorých karteziánske súradnice x, y spĺňajú nasledujúce podmienky:
- súradnica x je v definičnom obore funkcie f (teda x \in D(f))
- závislosť súradnice y od x je popísaná funkčným predpisom y=f(x) (pre každé x z D(f) je v grafe presne jeden bod, jeho súradnice sú x a f(x))
Príklad: graf, definičný obor, obor hodnôt funkcie
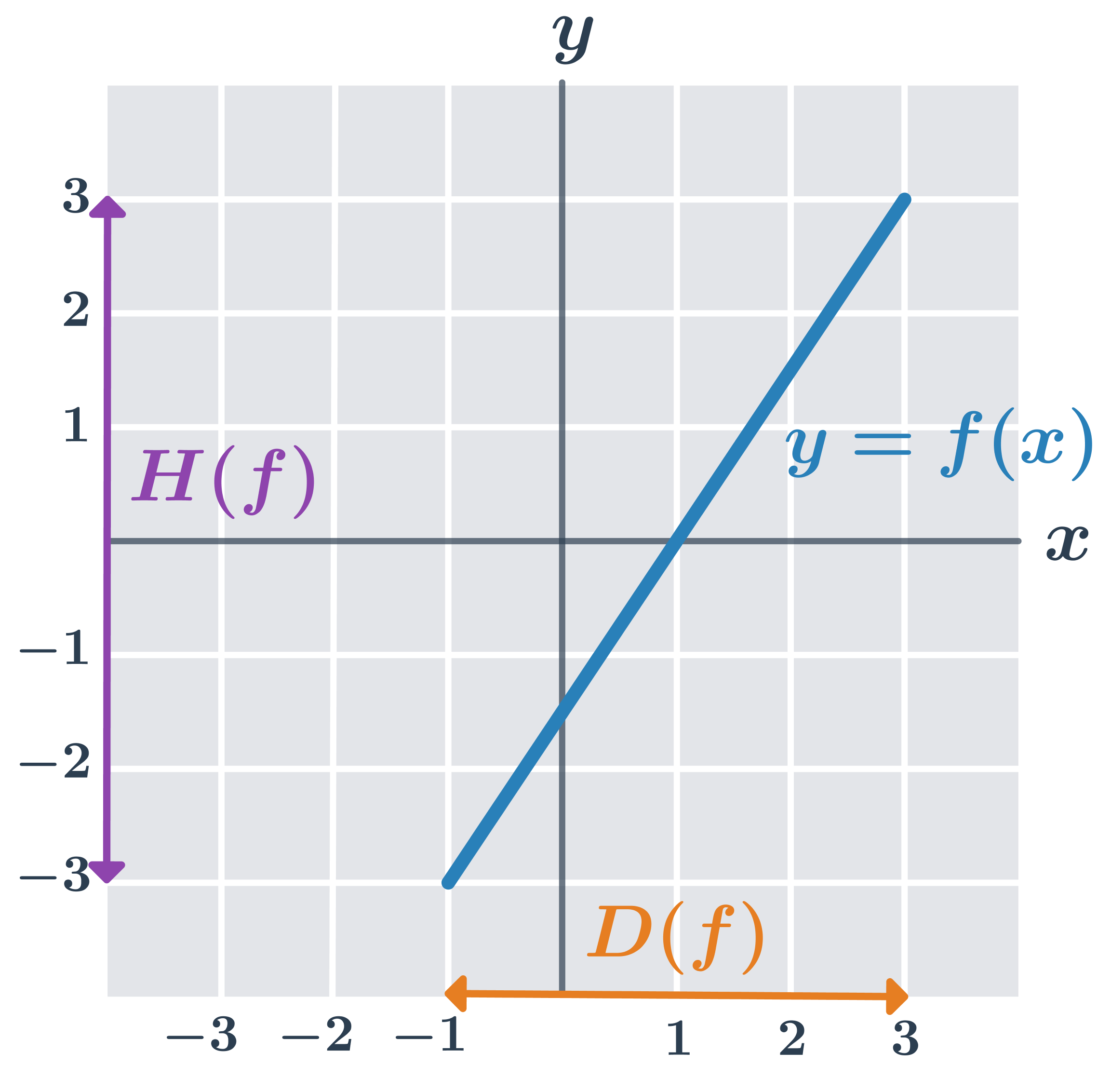
Na obrázku je graf funkcie y=2x-1 pre x\in \langle -1;3\rangle. Definičný obor je vyznačený na osi x, obor hodnôt na osi y.
Grafy lineárnych funkcií
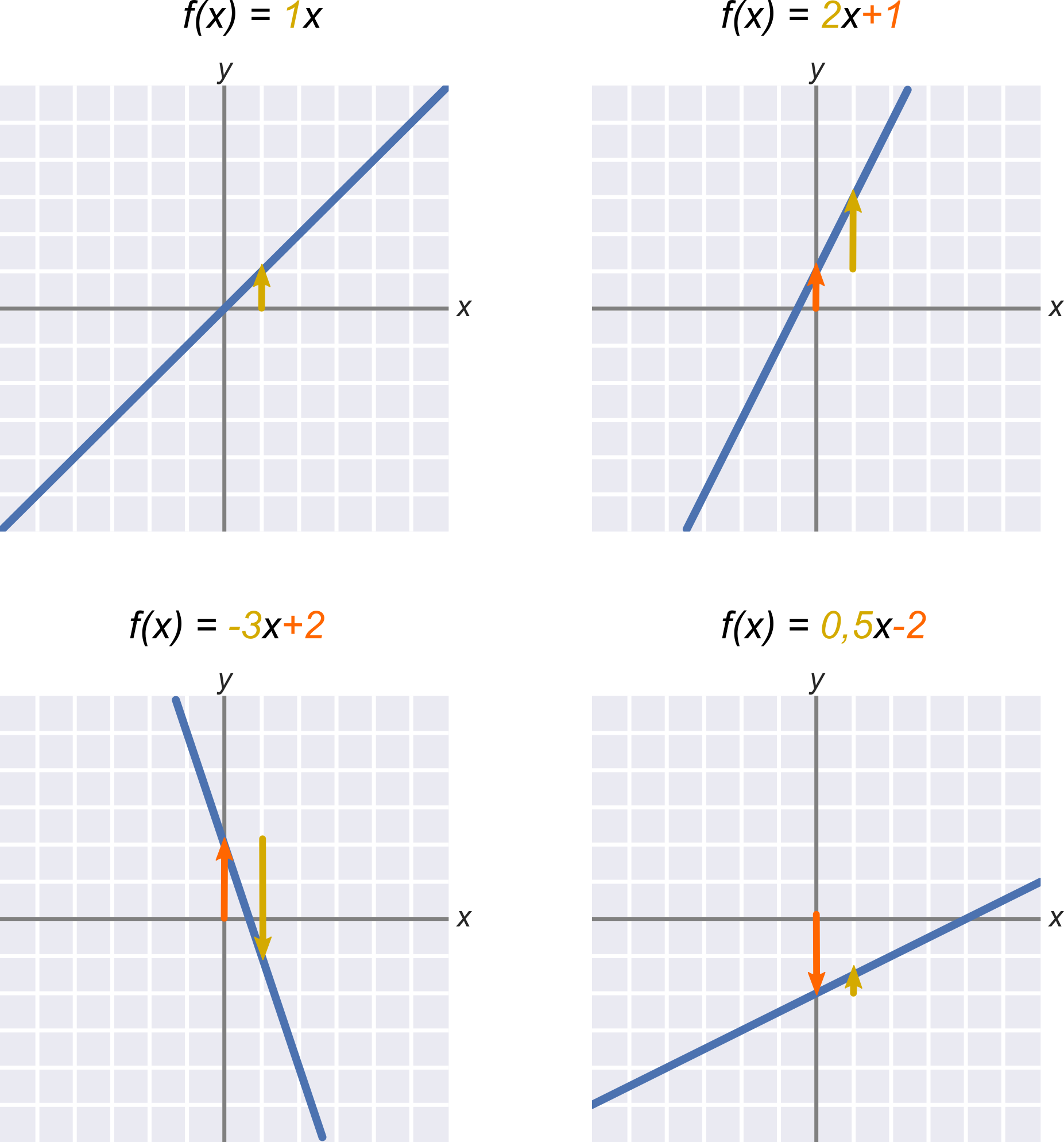
Lineárnu funkciu môžeme vždy zapísať v tvare f(x) = a\cdot x + b, kde a a b sú konštanty. Parameter a je smernica (tiež nazývaná sklon), parameter b je absolútny člen. Grafom lineárnej funkcie je priamka, pričom platí:
- Absolútny člen b udáva „zvislý posun“. Je to priesečník priamky s osou y. V uvedených príkladoch je vyznačený oranžovou farbou.
- Smernica a udáva sklon priamky, čo môžeme vyjadriť ako „o koľko jednotiek na osi y sa priamka posunie za jednu jednotku na osi x“. V uvedených príkladoch je smernica vyznačená žltou farbou.
Dôležité sú znamienka (naznačené v obrázkoch šípkami). Kladný absolútny člen znamená posun hore, záporný absolútny člen znamená posun dole. Kladná smernica znamená stúpajúcu priamku, záporná smernica znamená klesajúcu priamku.
Grafy kvadratických funkcií
Kvadratickú funkciu je možné vyjadriť v tvare f(x) = ax^2 + bx + c, kde a\neq 0. Grafom kvadratickej funkcie je parabola. Tento graf zobrazuje funkciu 0{,}5 x^2 + x - 4:
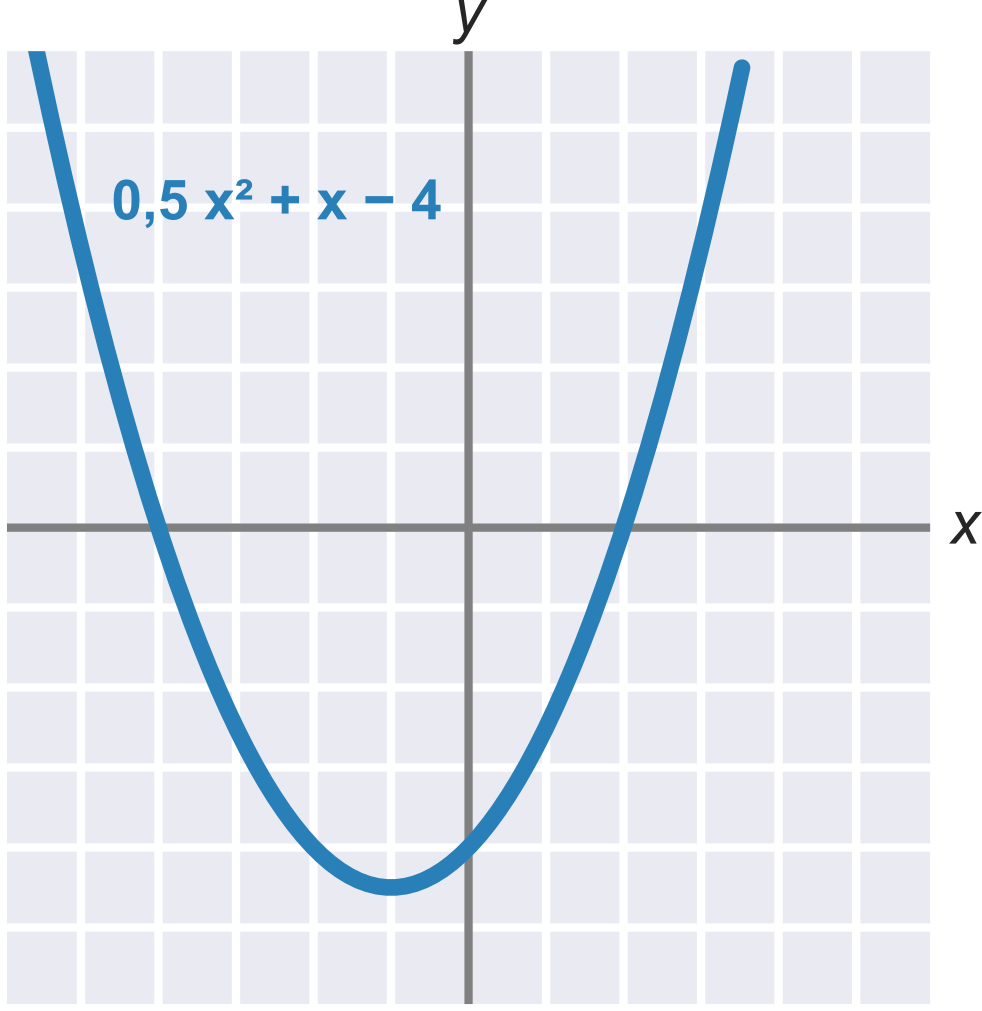
Priesečníky s osou x sú riešenia kvadratickej rovnice ax^2 + bx + c = 0. Pre vyššie uvedený príklad 0{,}5 x^2 + x - 4 sú týmito riešeniami x_1 = -4 a x_2 = 2.
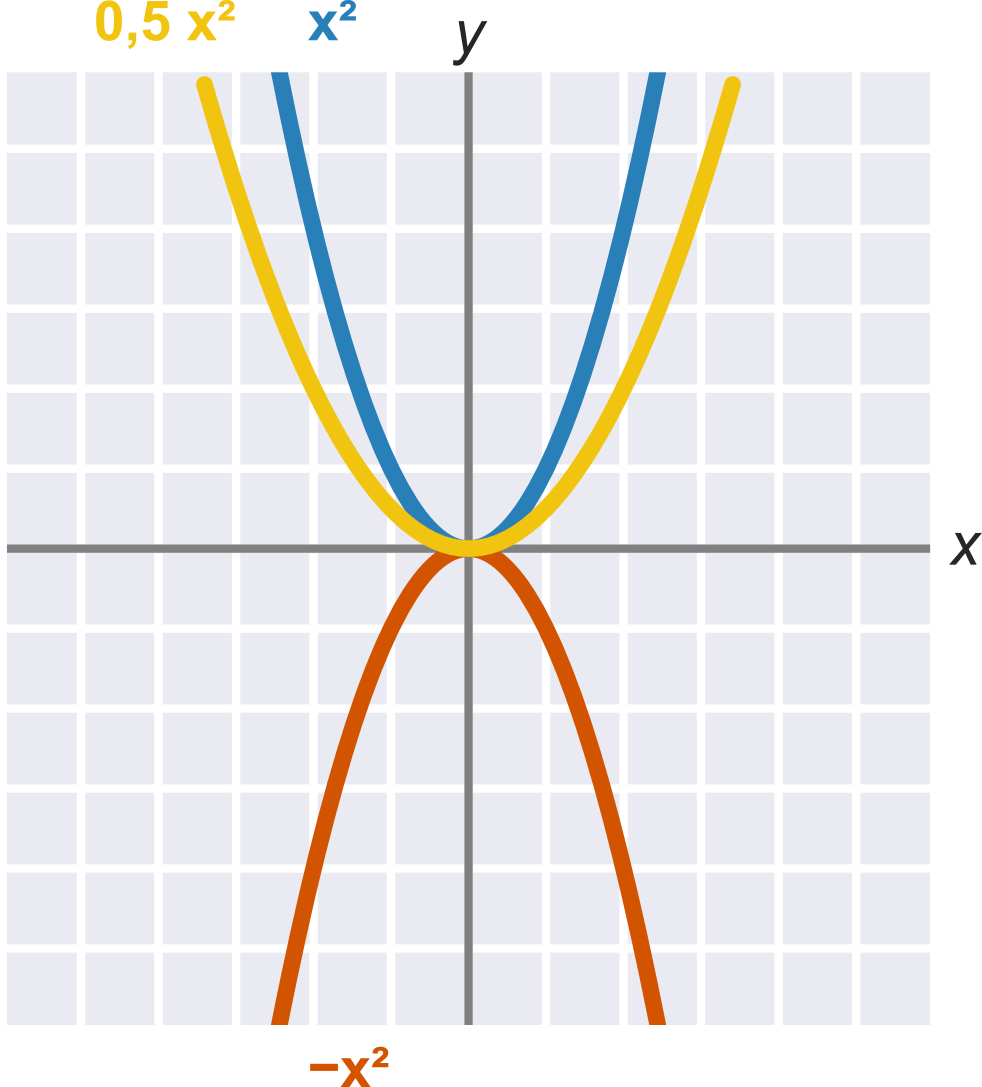
Kvadratický koeficient a ovplyvňuje základnú podobu paraboly:
- Ak je a > 0, „smeruje parabola hore“ (presnejšie: je to zdola ohraničená, konvexná funkcia).
- Ak je a \lt 0, „smeruje parabola dole“ (presnejšie: je to zhora ohraničená, konkávna funkcia).
- Veľkosť kvadratického koeficientu a ovplyvňuje, ako je parabola „široká“.
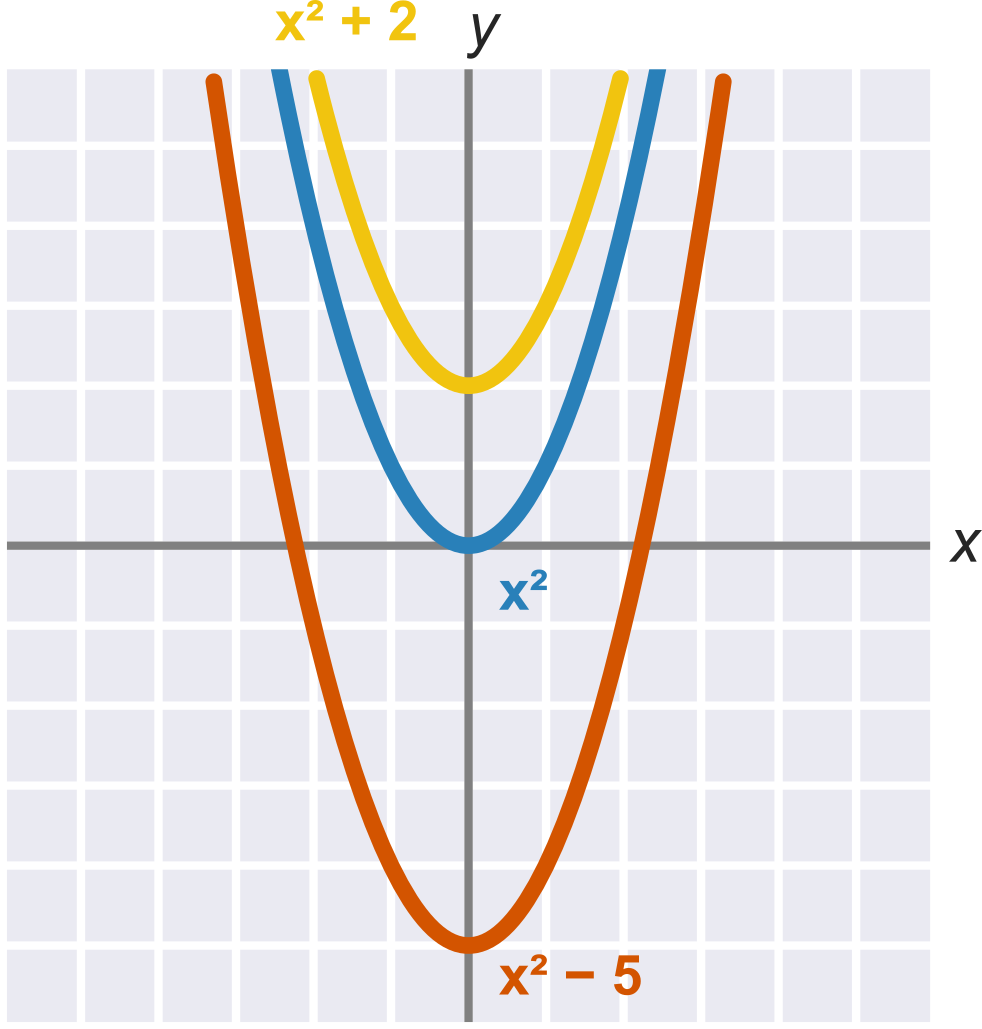
Konštantný člen c ovplyvňuje posun paraboly – udáva priesečník s osou y.
Grafy funkcií s absolútnou hodnotou
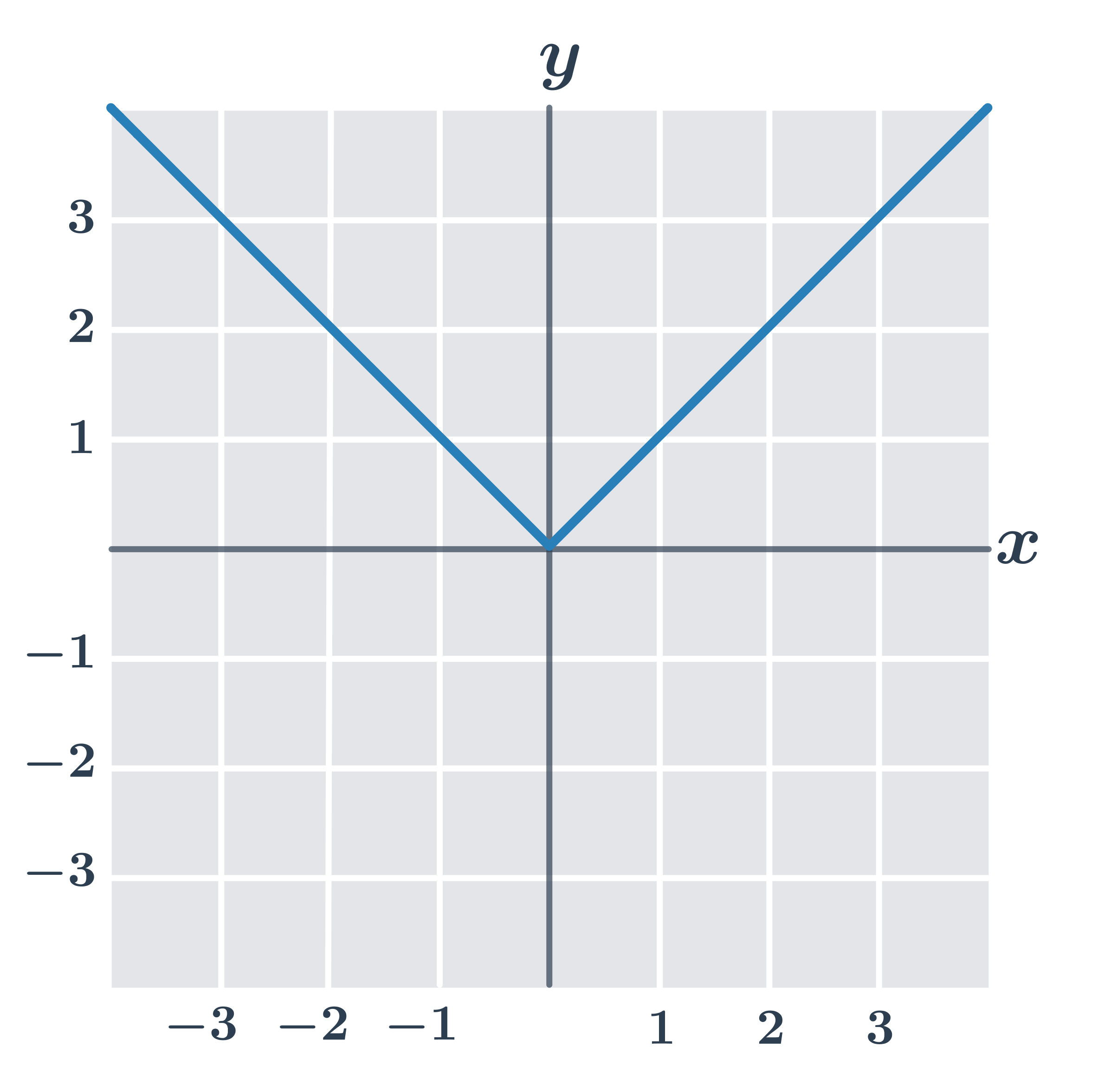
Na obrázku je graf funkcie y=|x|. Tento graf tvoria dve polpriamky s počiatkom v bode [0;0], pretože pre absolútnu hodnotu platí:
- absolútna hodnota kladného čísla je rovná tomuto číslu: |x|=x
- absolútna hodnota záporného čísla je rovná opačnému číslu: |x|=-x
- absolútna hodnota čísla nula je rovná nule: |0|=0
| x \gt 0 | Grafom funkcie y=|x| je polpriamka s počiatkom v bode [0;0] daná rovnicou y=x. |
| x \lt 0 | Grafom funkcie y=|x| je polpriamka s počiatkom v bode [0;0] s rovnicou y=-x. |
| x = 0 | Bod [0;0] je počiatok polpriamok, ktoré vytvoria graf funkcie y=|x|. |
Ak chceme nakresliť graf funkcie y=|f(x)| postupujeme tak, že nakreslíme graf y=f(x) a potom záporné funkčné hodnoty nahradíme opačnými. V oblasti, kde sú funkčné hodnoty záporné, sa teda graf preklopí okolo osi x.
Príklad 1: graf funkcie y=|x-1|
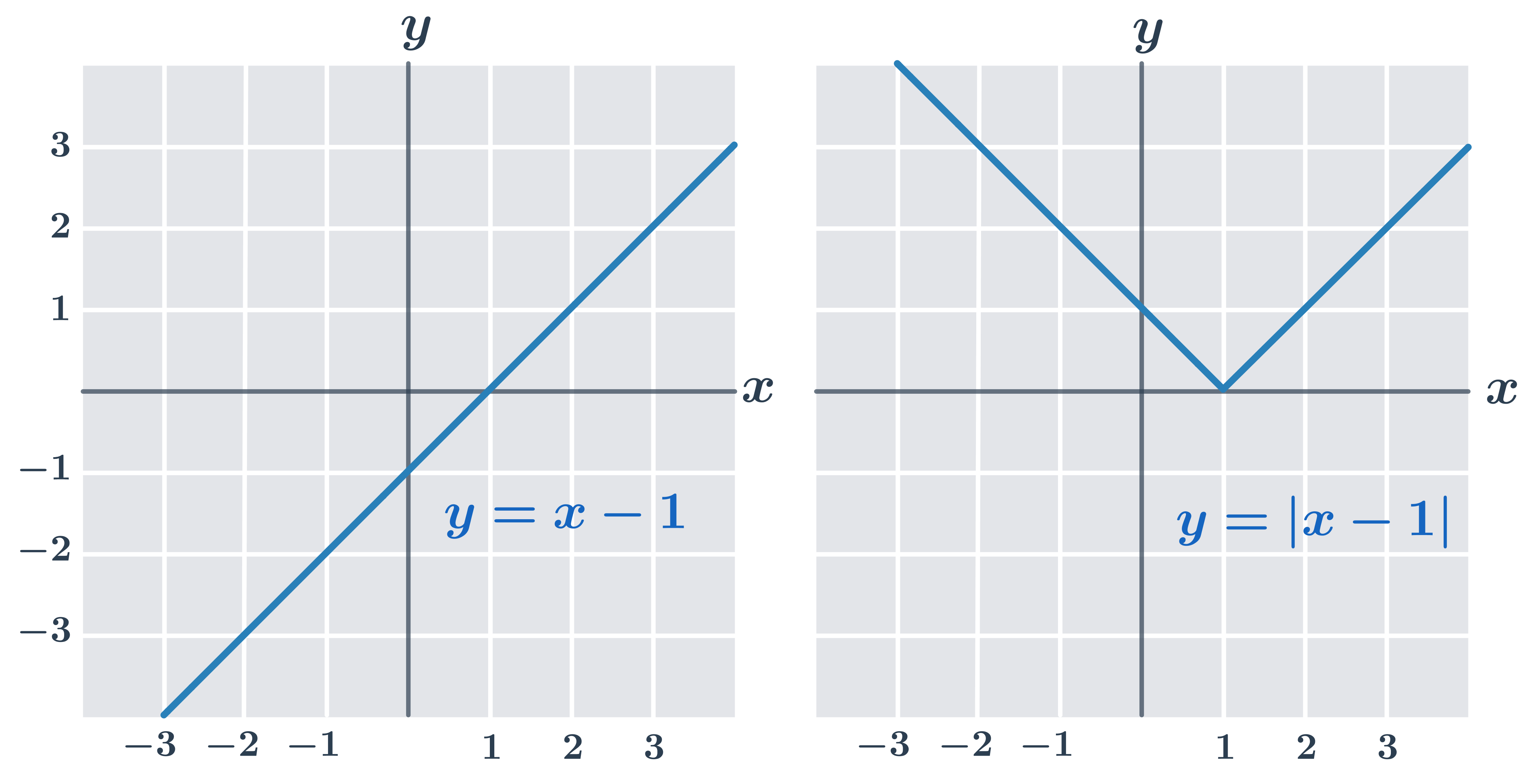
| Pre čísla x \lt 1 má funkcia y=x-1 záporné funkčné hodnoty. |
| Funkcia y=|x-1| má v intervale (-\infty;1) opačné hodnoty než funkcia y=x-1 (graf y=|x-1| je voči grafu y=x-1 v tomto intervale preklopený podľa osi x). |
| V intervale (1;\infty) sú grafy funkcií y=x-1 a y=|x-1| rovnaké. |
Príklad 2: graf funkcie y=|x^2-4|
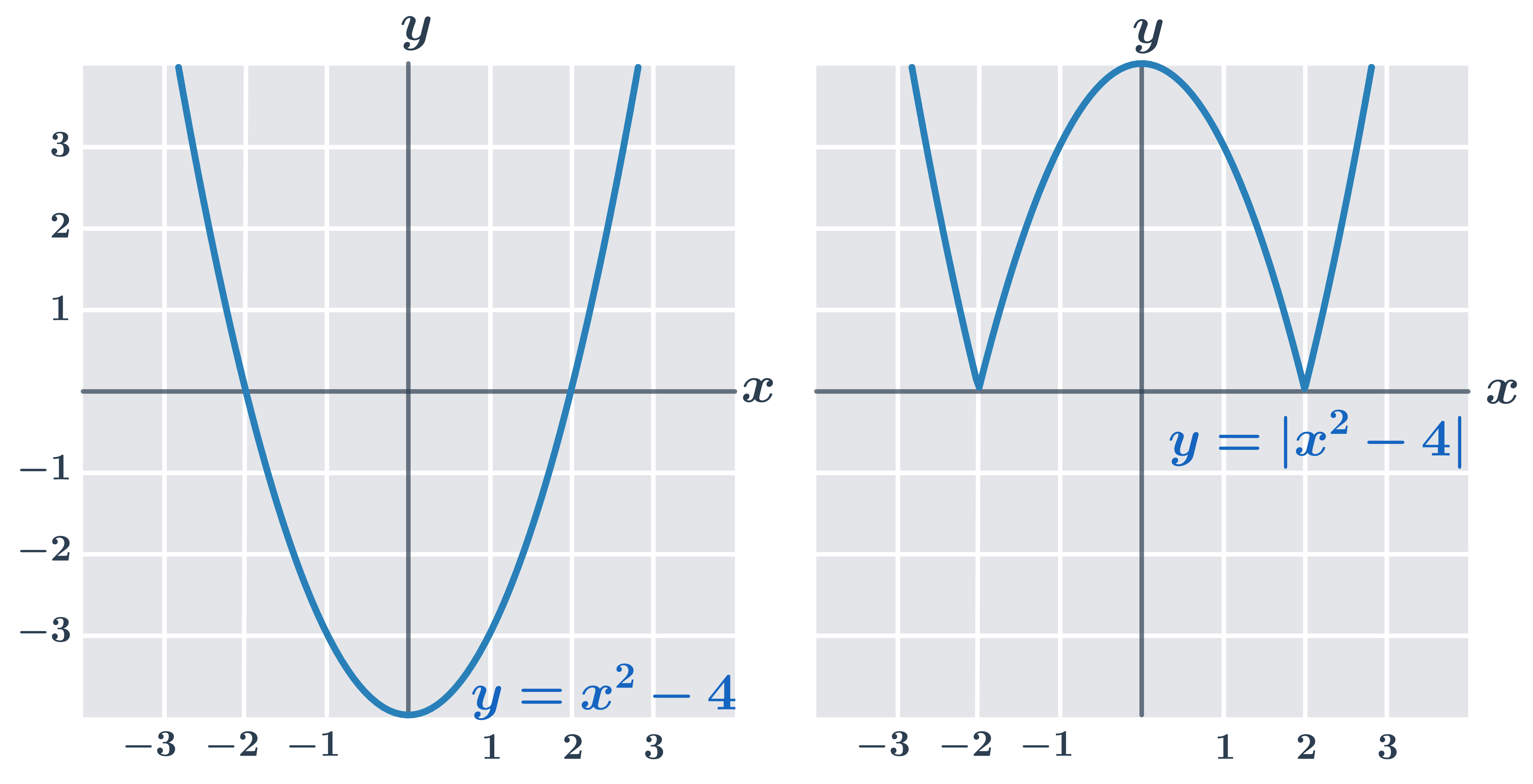
| V intervale (-2;2) má funkcia y=x^2-4 záporné funkčné hodnoty. |
| Funkcia y=|x^2-4| má v intervale (-2;2) opačné hodnoty než funkcia y=x^2-4 (graf je preklopený podľa osi x). |
| V intervaloch (-\infty;-2) a (2;\infty) sú grafy funkcií y=x^2-4 a y=|x^2-4| rovnaké. |
Grafy lineárnych lomených funkcií
Grafom lineárnej lomenej funkcie je hyperbola, ktorá má asymptoty rovnobežné so súradnicovými osami x a y.
Asymptota rovnobežná s osou y prechádza bodom, ktorý nepatrí do definičného oboru a má teda rovnicu: x =-\frac{d}{c}.
Na nájdenie rovnice asymptoty rovnobežnej s osou x vydelíme čitateľa a menovateľa a funkčný predpis y =\frac{ax+b}{cx+d} upravíme na tvar y =\frac{a}{c}+\frac{n}{ax+b}. Asymptota rovnobežná s osou x má rovnicu: y =\frac{a}{c}.
Priesečník grafu s osou x je bod, pre ktorý ax+b=0. V tomto bode je hodnota funkcie nulová, teda čitateľ zlomku \frac{ax+b}{cx+d} je nulový.
Priesečník grafu s osou y je bod, ktorý dostaneme dosadením hodnoty x=0 do funkčného predpisu.
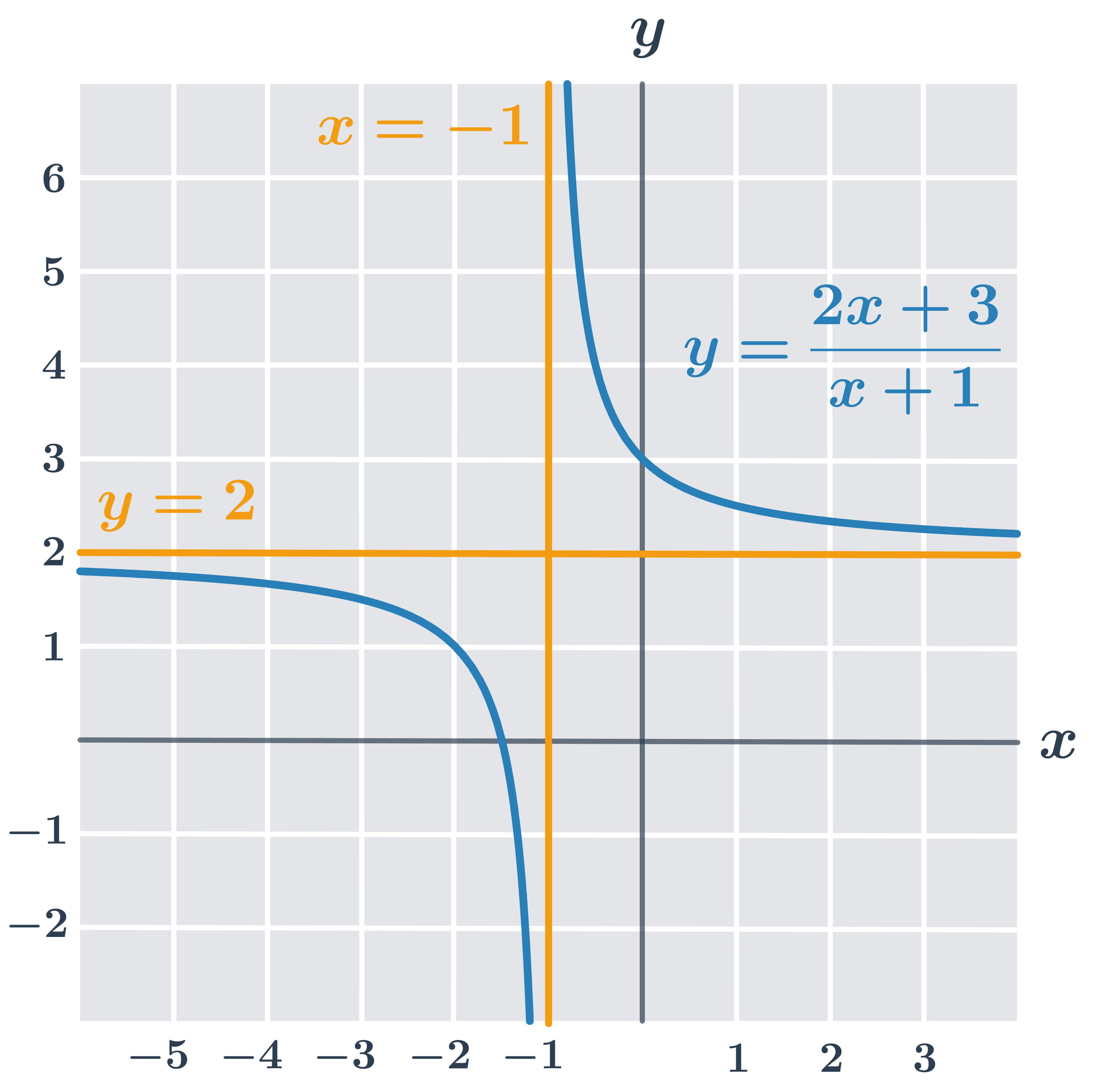
Príklad – funkcia y =\frac{2x+3}{x+1}
Rozoberme si graf funkcie z obrázka vyššie:
- definičný obor D(f)=\R - \{-1\}, pretože x+1\neq0
- asymptota rovnobežná s osou y má rovnicu x =-1 (pre x=-1 nie je funkcia definovaná, toto číslo neleží v jej definičnom obore)
- asymptota rovnobežná s osou x má rovnicu y =2, čo zistíme úpravou funkčného predpisu: y =\frac{2x+3}{x+1}=2+\frac{1}{x+1}
- priesečník grafu s osou x je bod [0;-\frac{3}{2}] (riešenie rovnice: 2x+3=0)
- priesečník grafu s osou y je bod [3;0], dosadením hodnoty x=0 do y =\frac{2x+3}{x+1}
Grafy mocninových funkcií
Grafy základných mocninových funkcií y= x^n
pre párne n – graf je súmerný podľa osi y, D(f)=\R, H(f)=\langle0, \infty)
pre nepárne n – graf je súmerný podľa počiatku, D(f)=\R, H(f)=\R
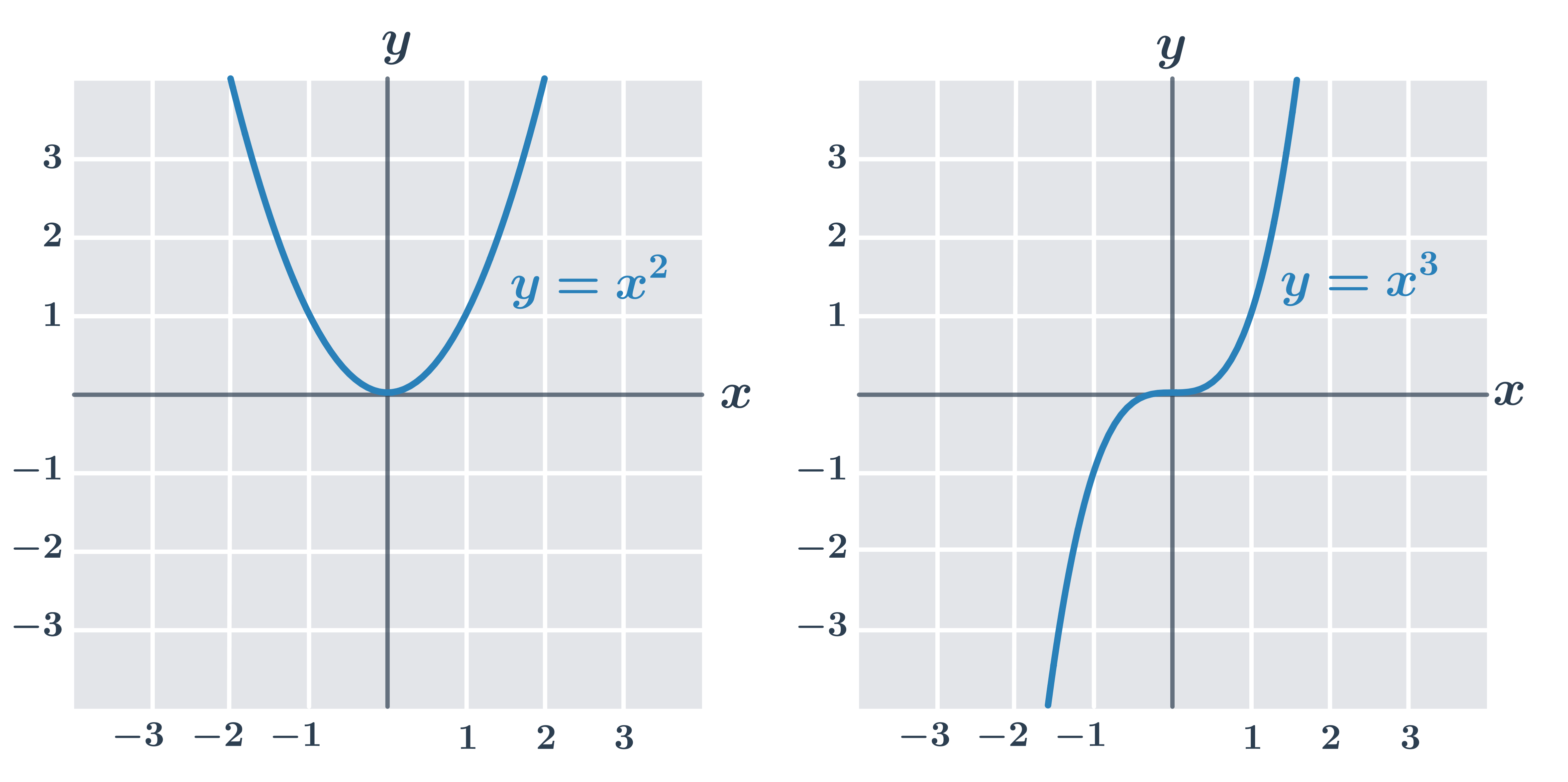
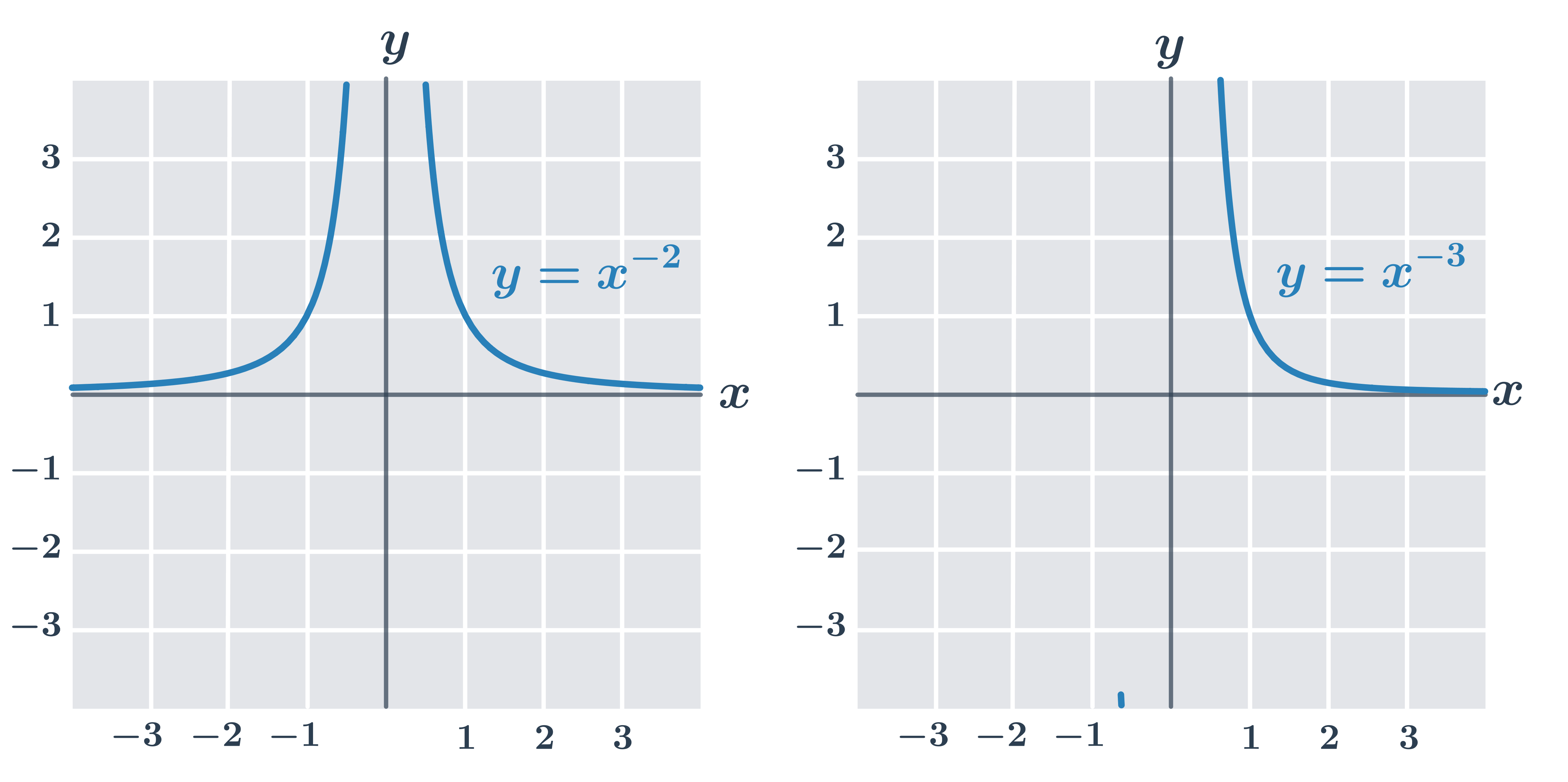
Grafy mocninových funkcií so záporným exponentom y= x^{-n}
pre párne n – graf súmerný podľa osi y, D(f)=\R- \{0\}, H(f)=\langle0, \infty)
pre nepárne n – graf súmerný podľa počiatku, D(f)=\R - \{0\}, H(f)=\R - \{0\}
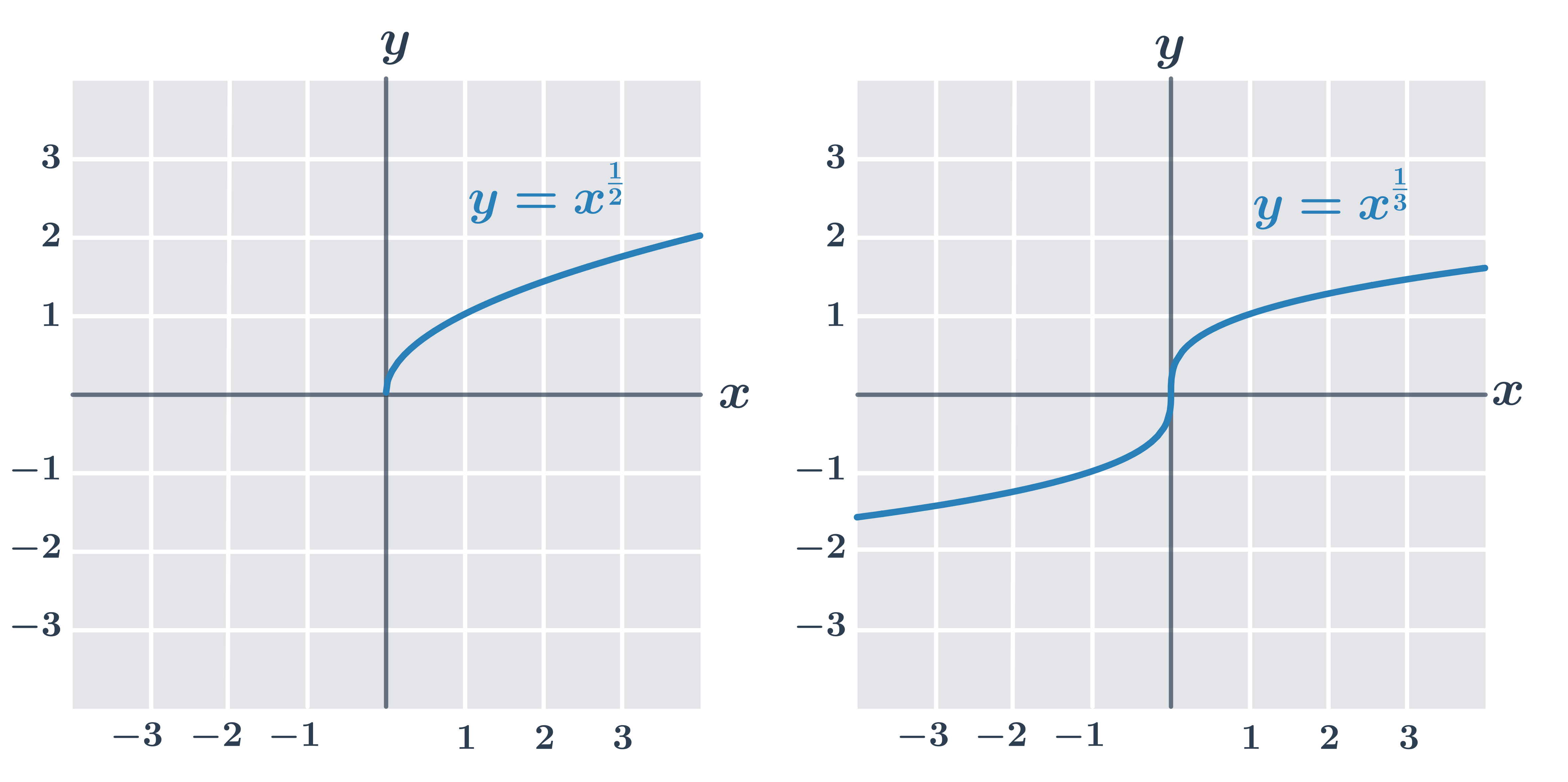
Grafy funkcií y= x^{\frac{1}{n}}:
pre párne n – funkcia y= x^{\frac{1}{n}} definovaná na kladných číslach, D(f)=\langle0, \infty), H(f)=\langle0, \infty)
pre nepárne n – funkcia y=x^n je jednoduchá, preto by sme mohli definovať n-tú odmocninu aj pre záporné čísla, ale často sa všetky n-té odmocniny pre párne aj nepárne n definujú pre jednoduchosť iba na intervale [0,\infty) (napr. ako príprava na prácu s mocninovými funkciami so všeobecnejšími racionálnymi exponentami) .
Poznámka: výpočty s mocninami a odmocninami
Pri výpočtoch s mocninami a odmocninami musíme byť obozretní; veľa pravidiel platí pre nezáporný základ (ak počítame s odmocninami), prípadne kladný základ (nulu môžeme odmocňovať, ale nesmieme deliť nulou). Príklady:
súčin odmocnín je odmocnina súčinu: pre nezáporné čísla ako základy odmocnín pravidlo platí, ak by sme chceli použiť pre záporný základ, nemusia nám v obore reálnych čísel vychádzať zmysluplné veci: \sqrt{-2} nie je definovaná, ale \sqrt{(-2)\cdot(-2)} je \sqrt{4} = 2
racionálne exponenty: malo by x^{\frac{2}{6}} byť to isté ako x^{\frac{1}{3}}? Exponent je „rovnaké racionálne číslo“, ale pre záporné x by vychádzali v prípade týchto dvoch predpisov iné funkčné hodnoty (6. odmocnina zo záporného x nie je definovaná, 6. odmocnina z druhej mocniny záporného čísla je kladná, a 3. odmocnina z x by bola pre záporné x záporná).
racionálne exponenty konkrétnejšie: čomu by sa malo rovnať (-8)^{\frac{2}{6}}? Máme (-8)^{\frac{1}{3}}=-2, ale zároveň \sqrt[6]{(-8)^2} = \sqrt[6]{64} = 2. Môžeme mať problém, keď budeme pravidlá, ktoré platia pre mocniny a odmocniny kladných a nezáporných čísel, skúšať používať aj pre záporné základy.
Vplyv úprav funkčného predpisu na graf mocninovej funkcie
Obrázok ukazuje niekoľko úprav funkcie y= x^3:
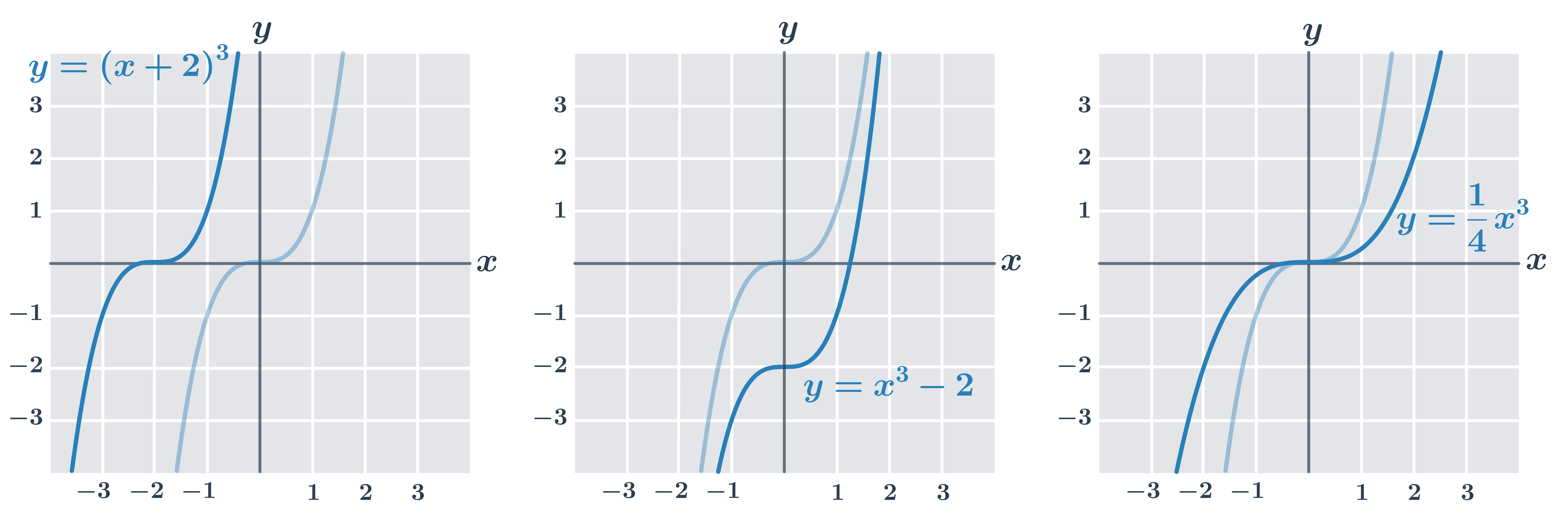
| y= (x+2)^3 | graf je posunutý v smere osi x |
| y=x^3-2 | graf je posunutý v smere osi y |
| y=\frac{1}{4} x^3 | graf bude natiahnutý alebo stlačený v smere osi y (v uvedenom grafe sa funkčné hodnoty zmenšia na štvrtinu, napríklad pre x=2 je hodnota funkcie y=\frac{1}{4} \cdot 2^3=2) |
Grafy goniometrických funkcií
Grafy základných goniometrických funkcií

Dopad úprav funkcie na graf

Obrázok ukazuje grafy niekoľkých úprav funkcie \sin(x).
| \sin(x+1) | graf má posunutú fázu (posun v smere osi x) |
| \sin(x)+1 | graf je posunutý v smere osi y |
| \sin(2x) | funkcia má zmenenú dĺžku periódy |
| 2\sin(x) | funkcia má zmenenú veľkosť amplitúdy |
Grafy exponenciálnych funkcií
Grafy exponenciálnych funkcií
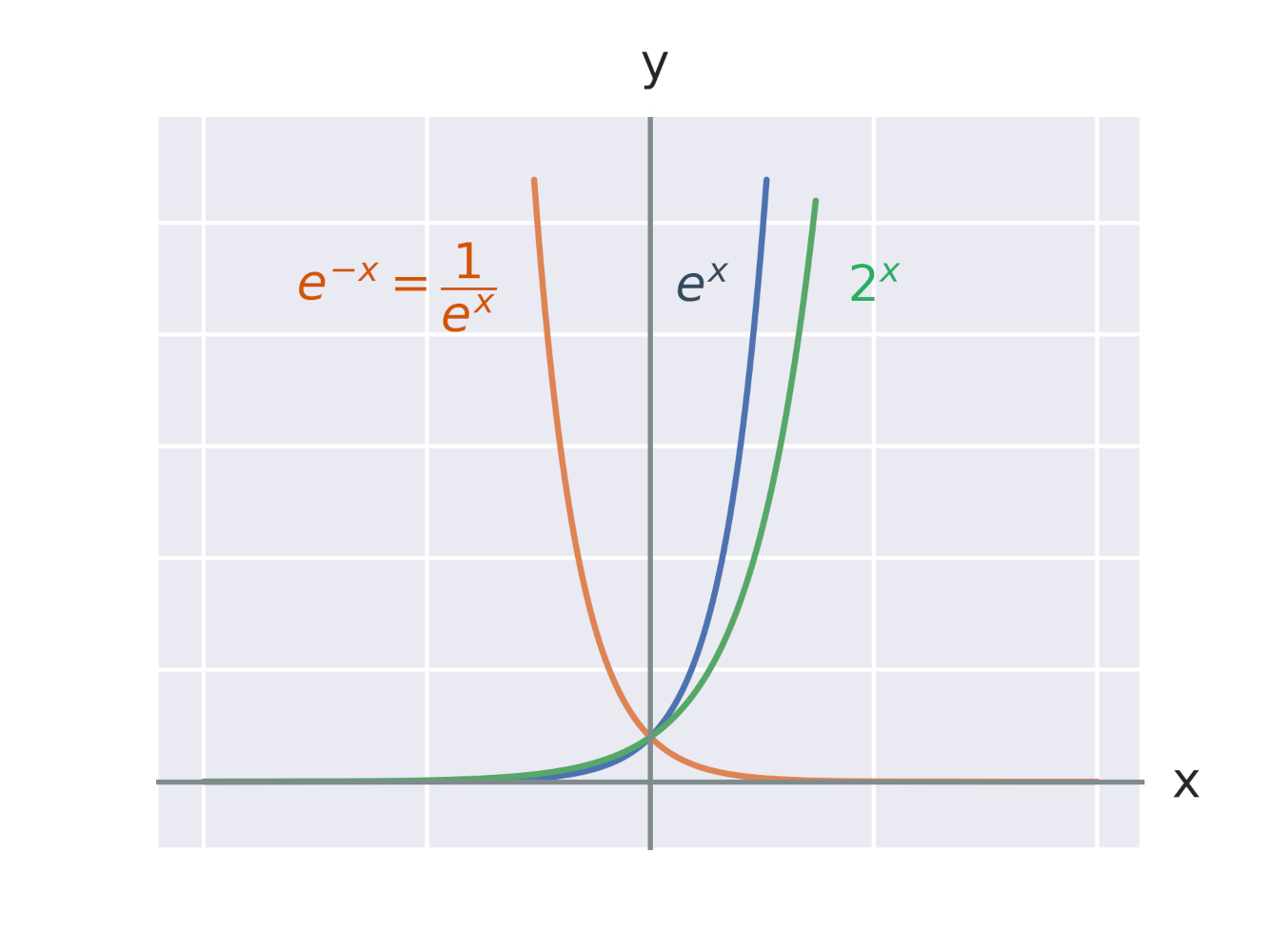
Grafom exponenciálnej funkcie je krivka s názvom exponenciála. Na obrázku sú grafy exponenciálnych funkcií so základmi 2 a e = 2{,}7 182 818 284\ldots. Vidíme tiež, že grafy funkcií e^x a e^{-x} sú spolu súmerné podľa osi y.
Efekt pripočítania konštanty k exponenciálnej funkcii
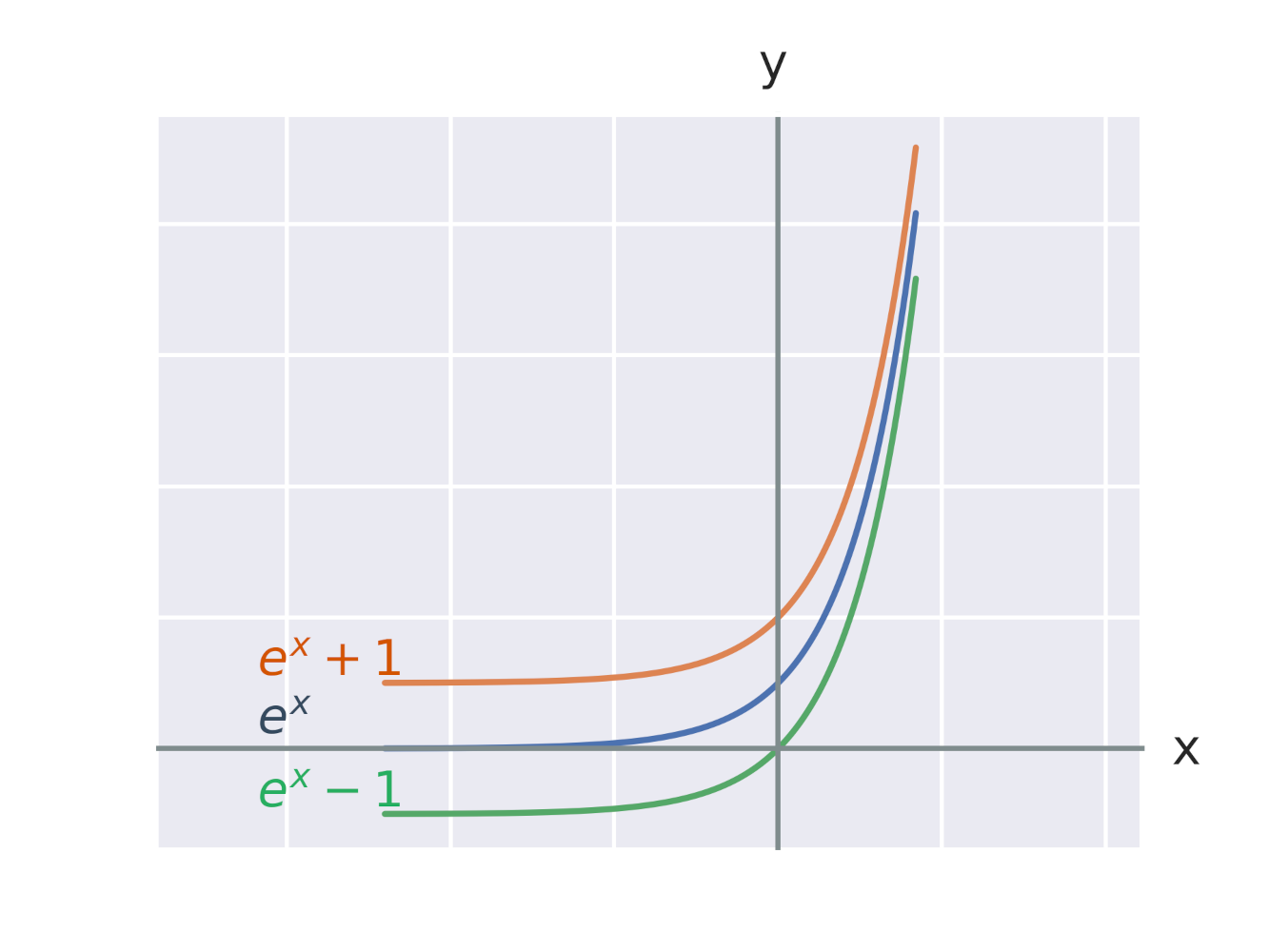
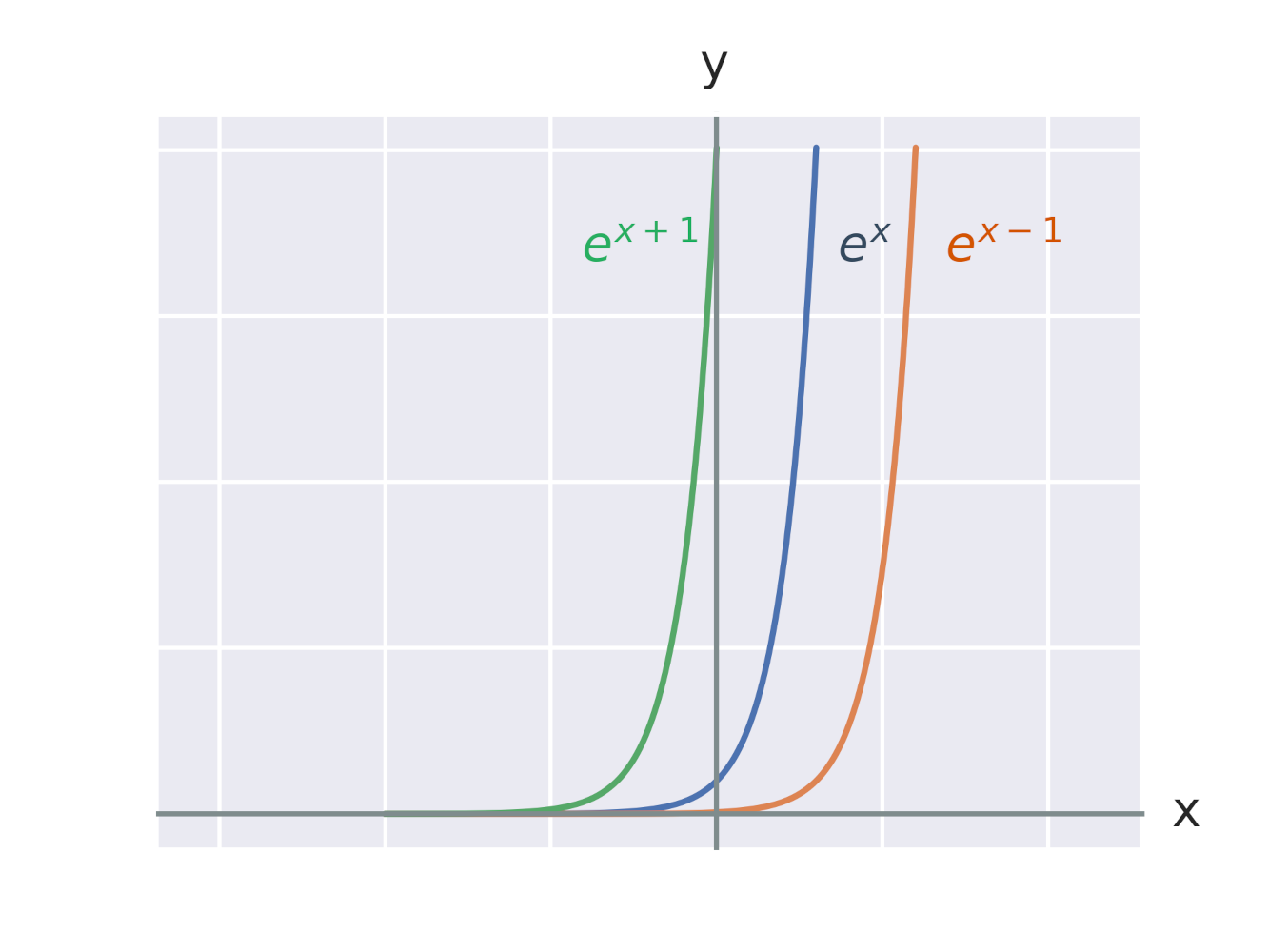
Efekt pripočítania konštanty k exponentu
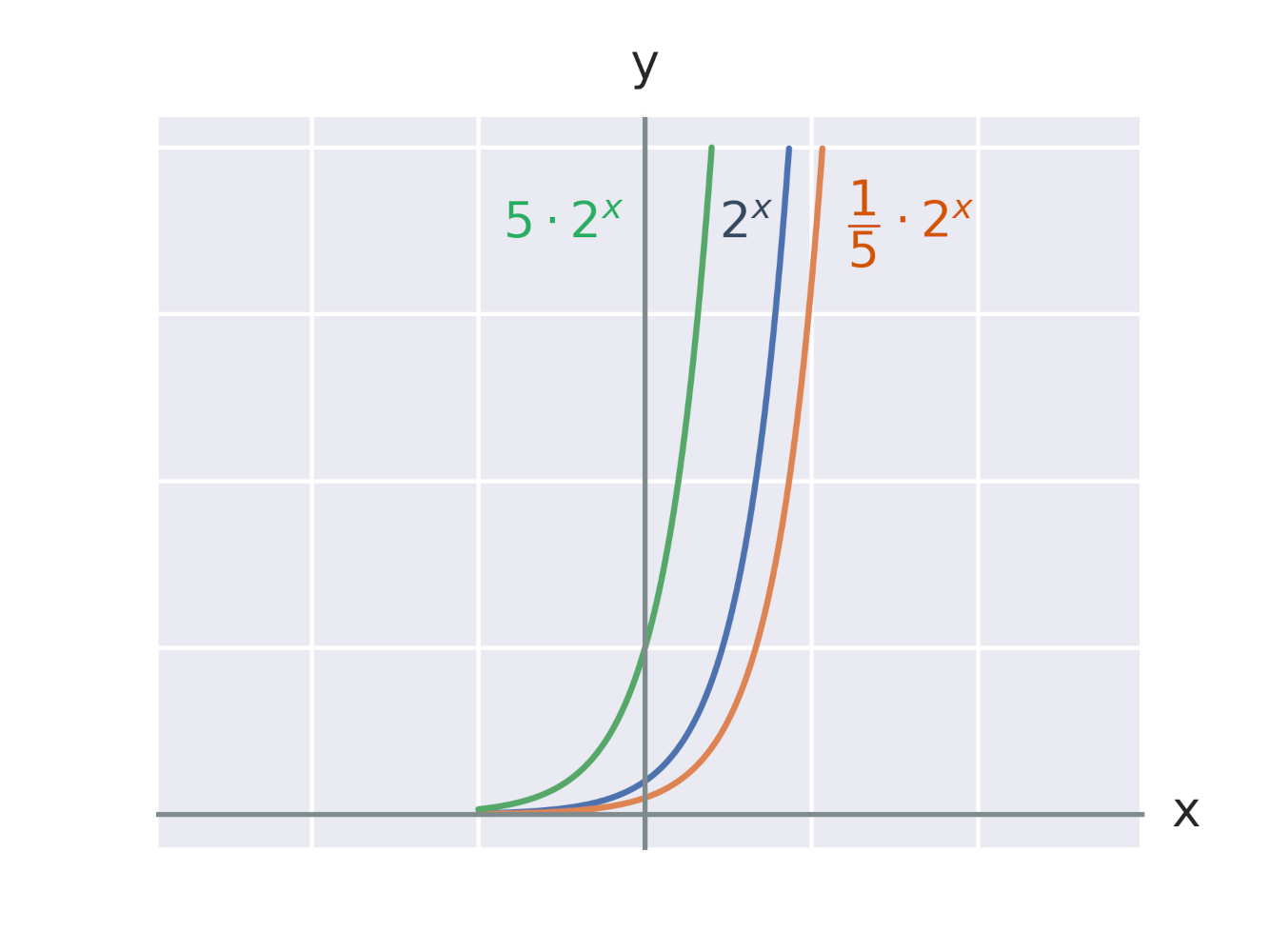
Efekt vynásobenia exponenciálnej funkcie konštantou
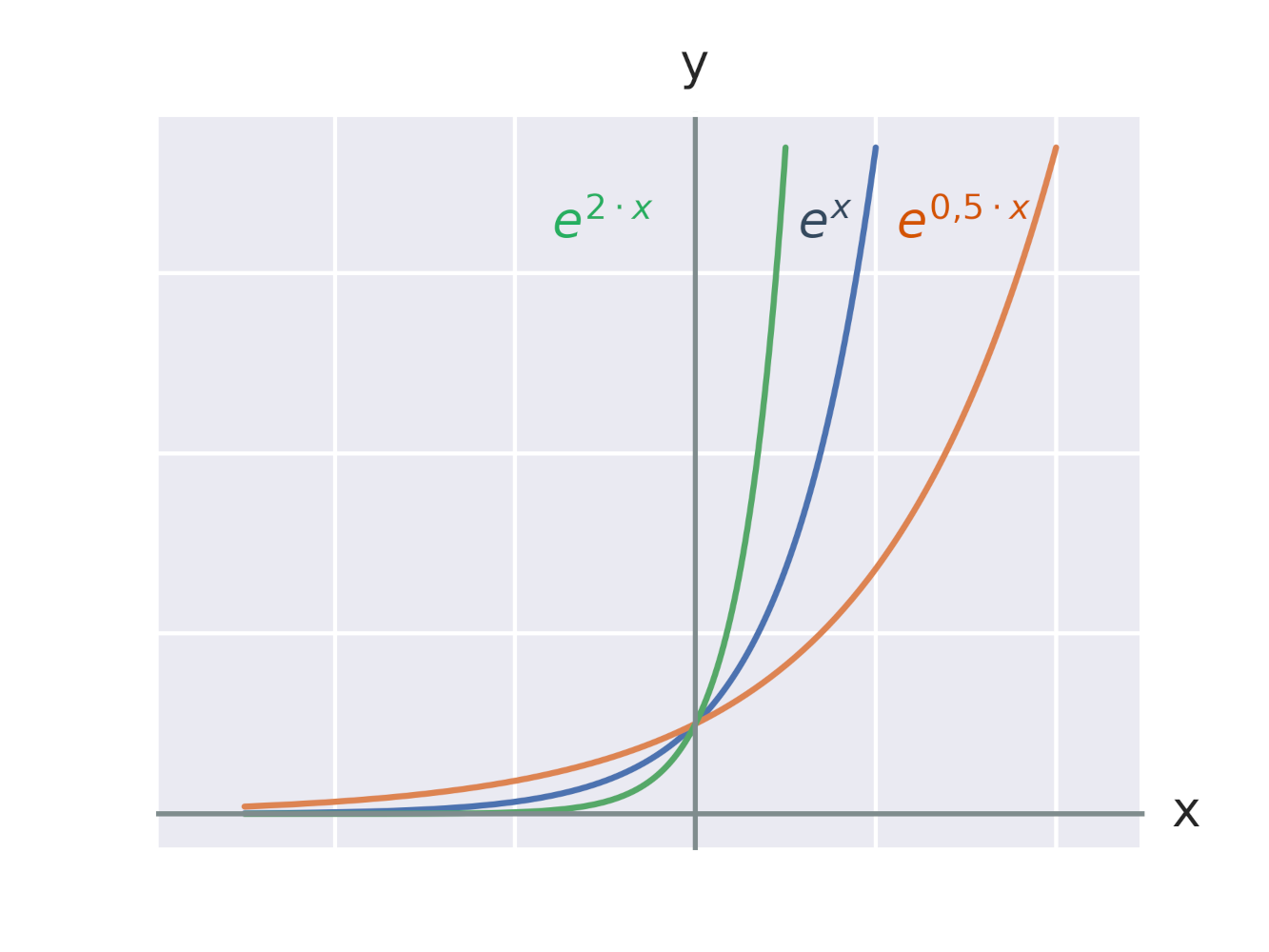
Efekt vynásobenia exponentu konštantou
Grafy logaritmických funkcií
Logaritmická funkcia je inverzná k exponenciálnej funkcii s rovnakým základom. Grafy dvoch navzájom inverzných funkcií sú osovo súmerné podľa osi prvého kvadrantu (teda priamky spĺňajúcej x=y).
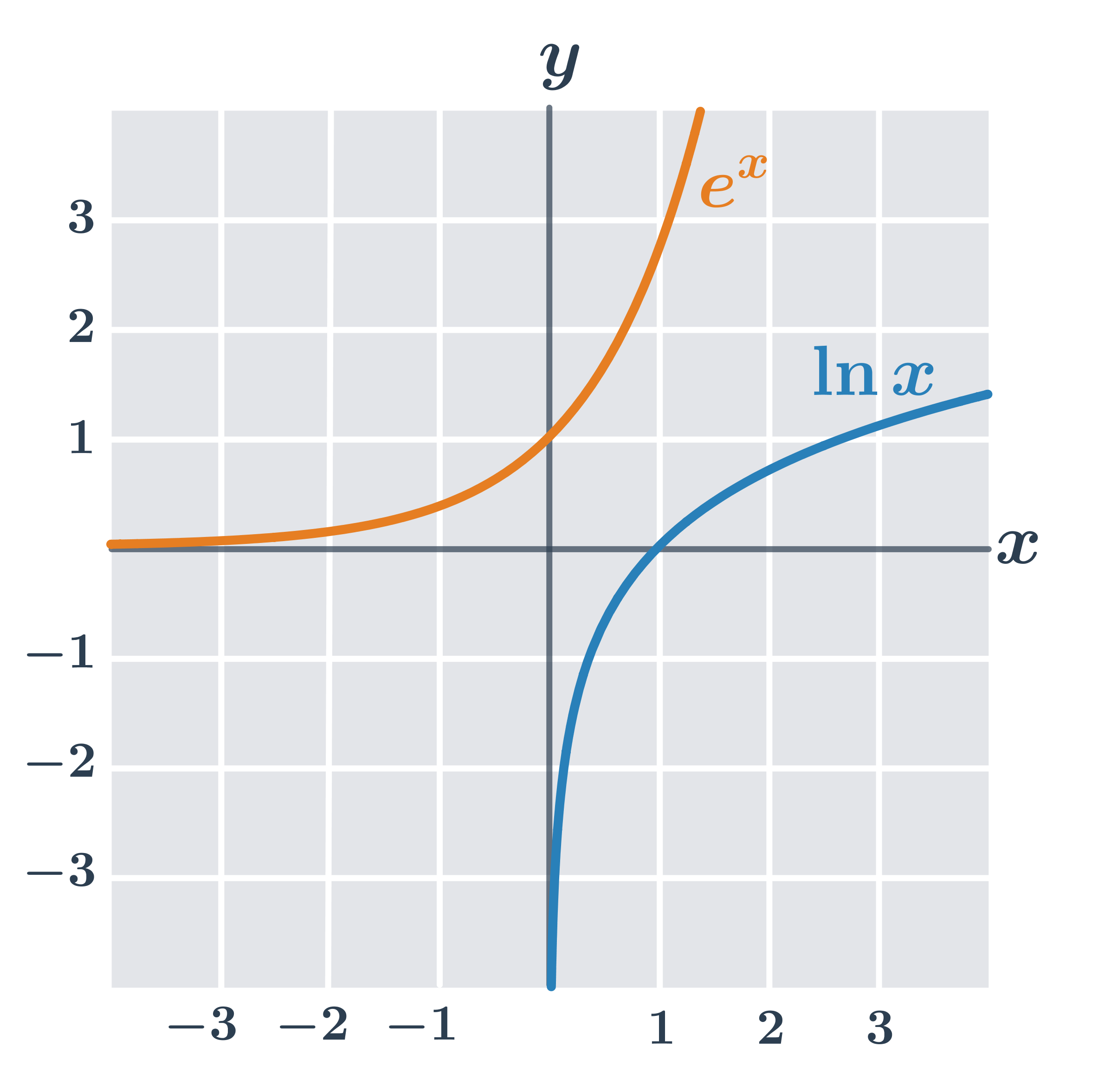
Na obrázku vidíme grafy logaritmických funkcií s rôznymi základmi 2, e, 10.
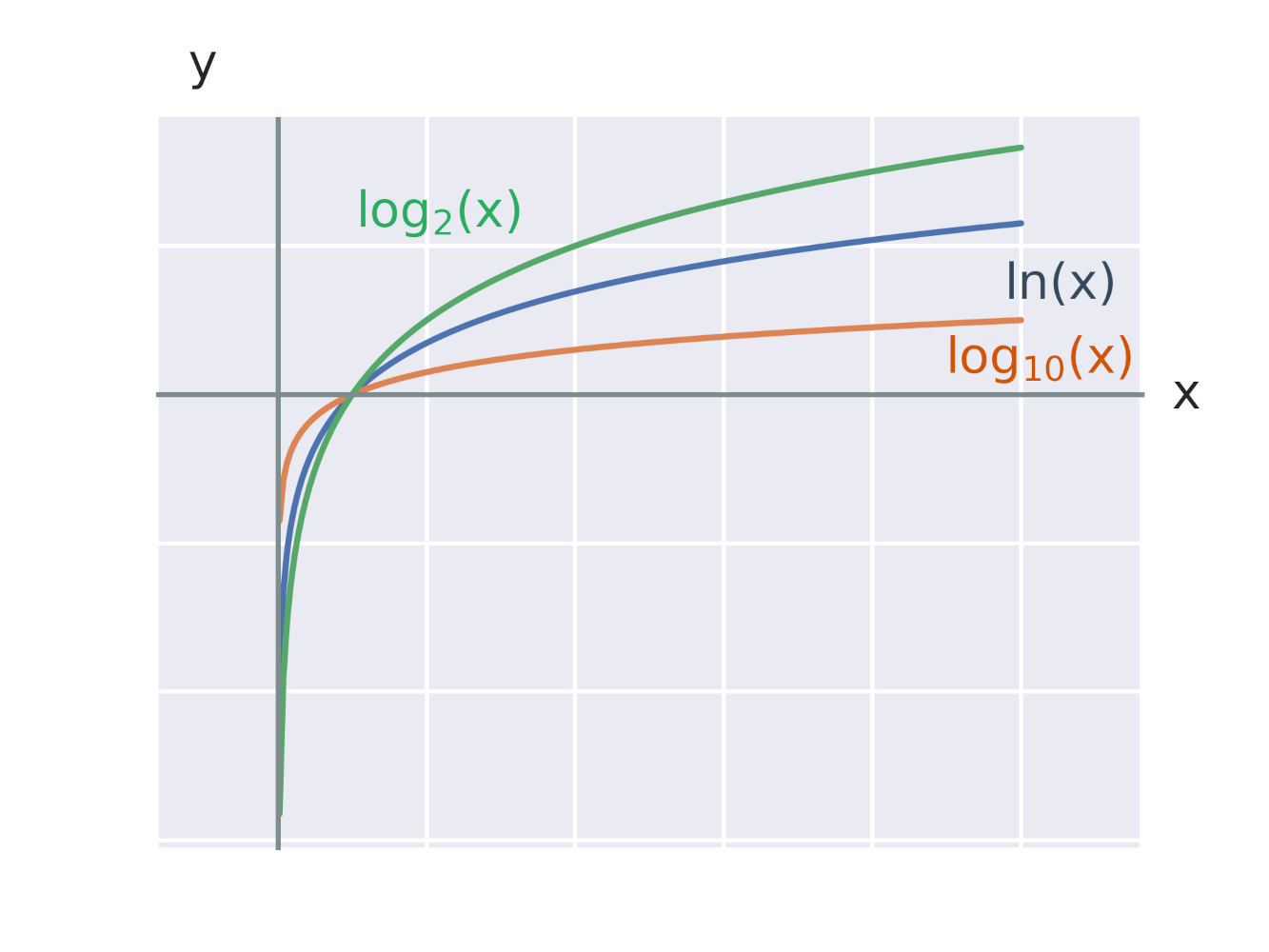
Značenie niektorých význačných logaritmických funkcií:
| funkcia | popis | značenie |
|---|---|---|
| \log_a x | všeobecne logaritmus x so základom a pre nejaké a >0, a\neq 1 | \log_a x |
| \log_e x | prirodzený logaritmus x | t u\ln x, v angl. textoch niekedy \log x |
| \log_{10} x | dekadický logaritmus x | tu \log x, v textoch slovenských aj angl. býva \log x, \log_{10}x |
| \log_2 x | binárny logaritmus x | tu \log_2 x, v textoch niekedy je aj \mathrm{lb}\;x |
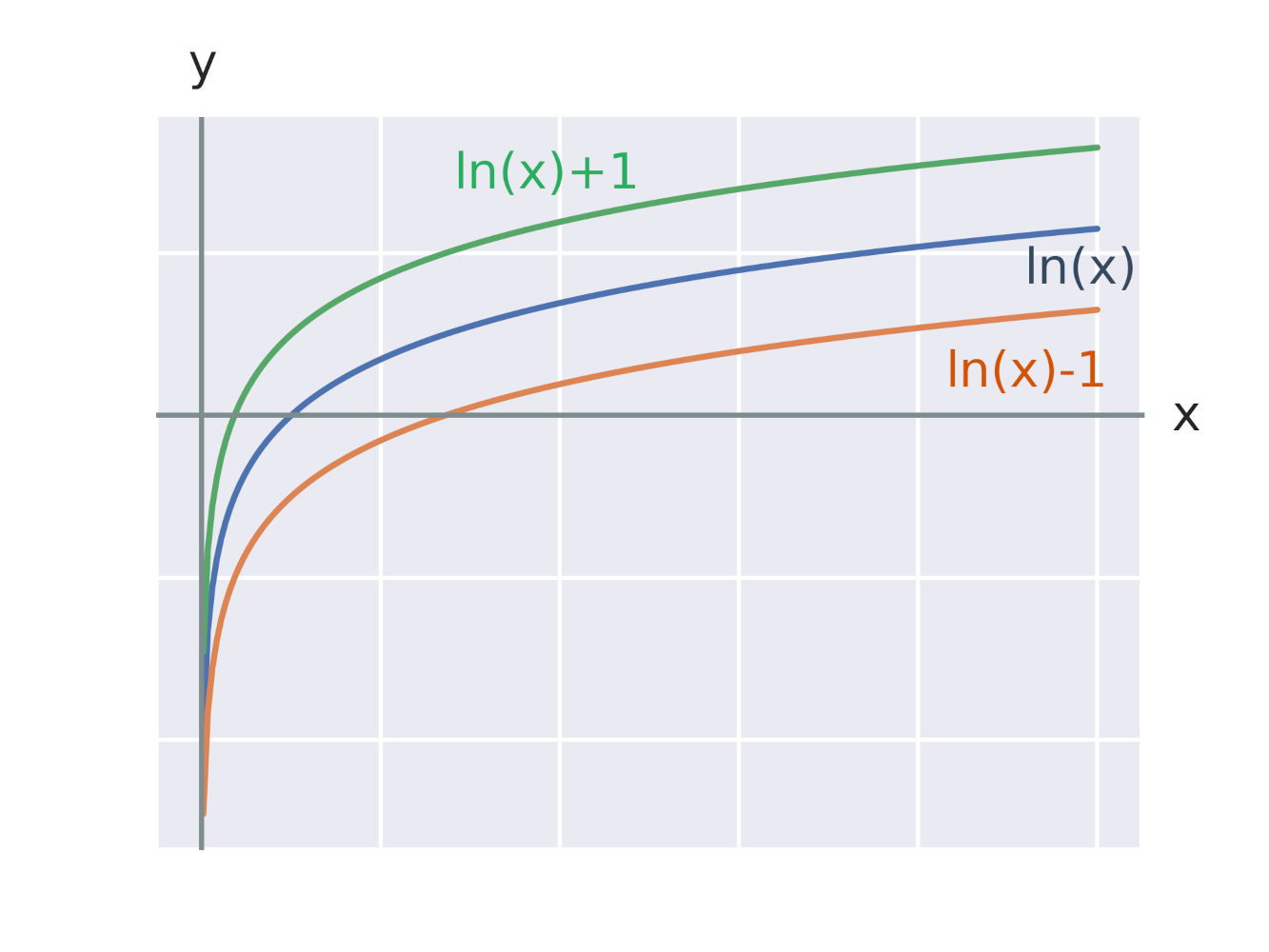
Efekt pripočítania konštanty k logaritmickej funkcii
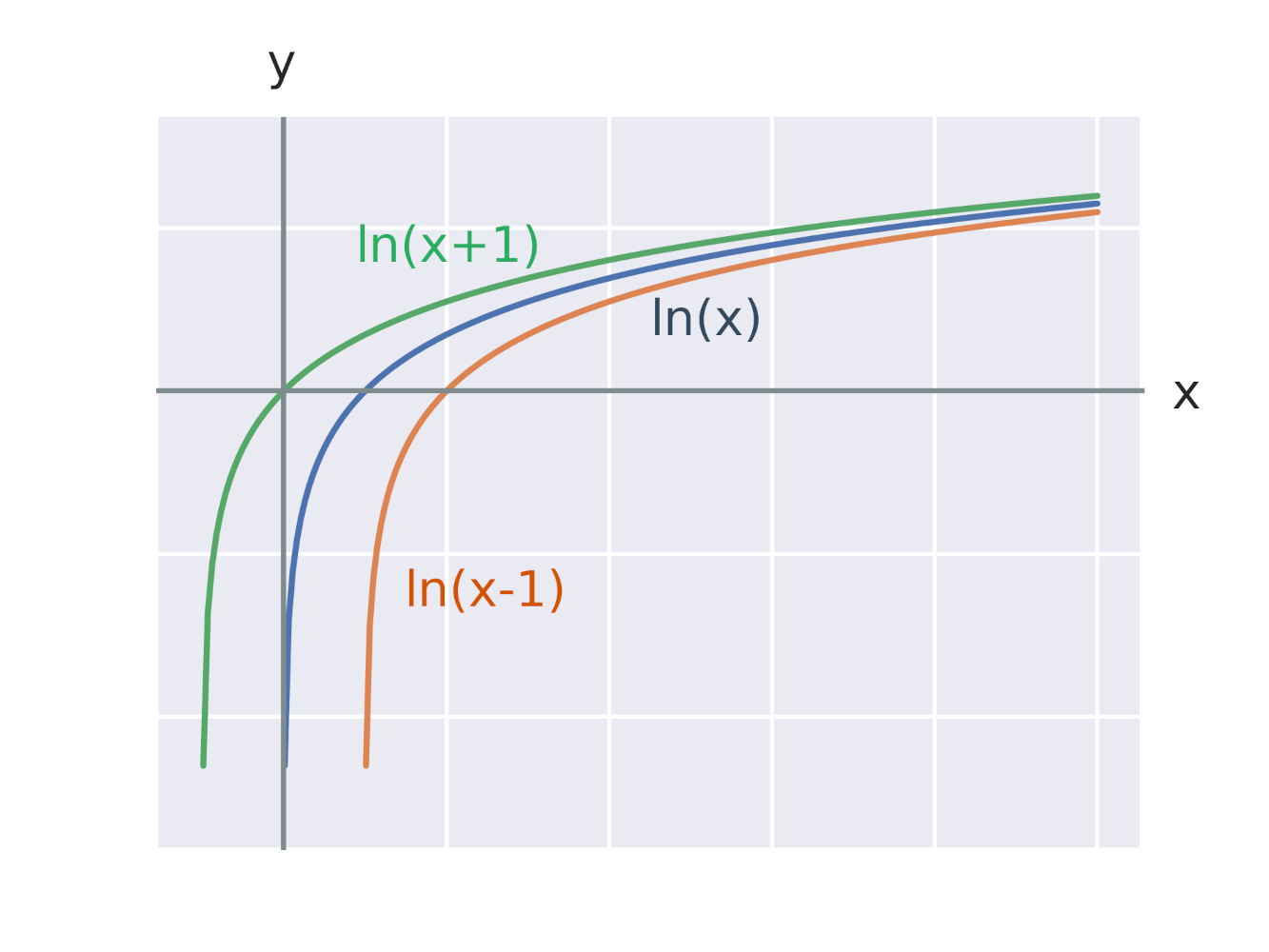
Efekt pripočítania konštanty k argumentu logaritmickej funkcie
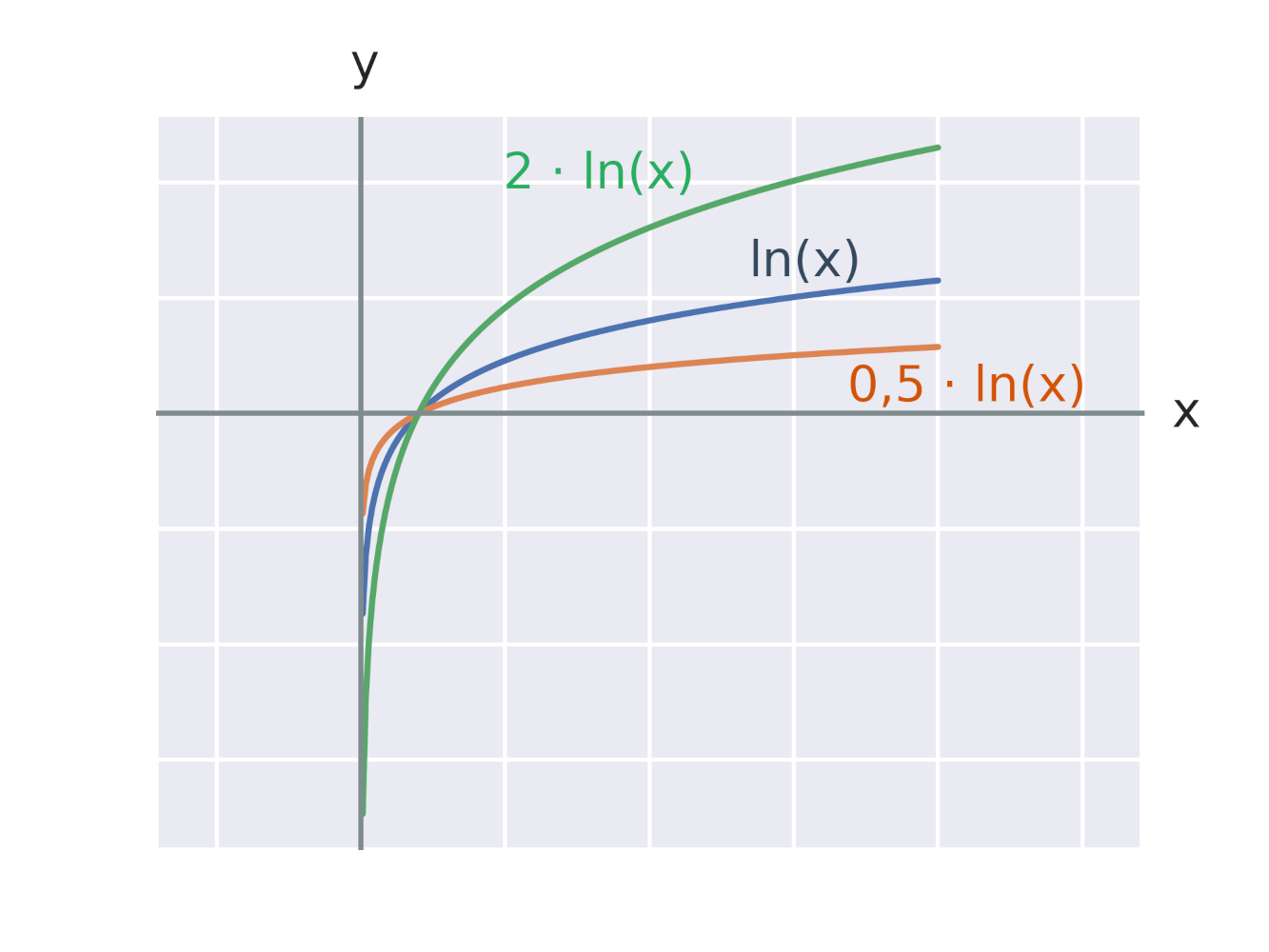
Efekt vynásobenia logaritmickej funkcie konštantou
Efekt vynásobenie argumentu logaritmickej funkcie konštantou
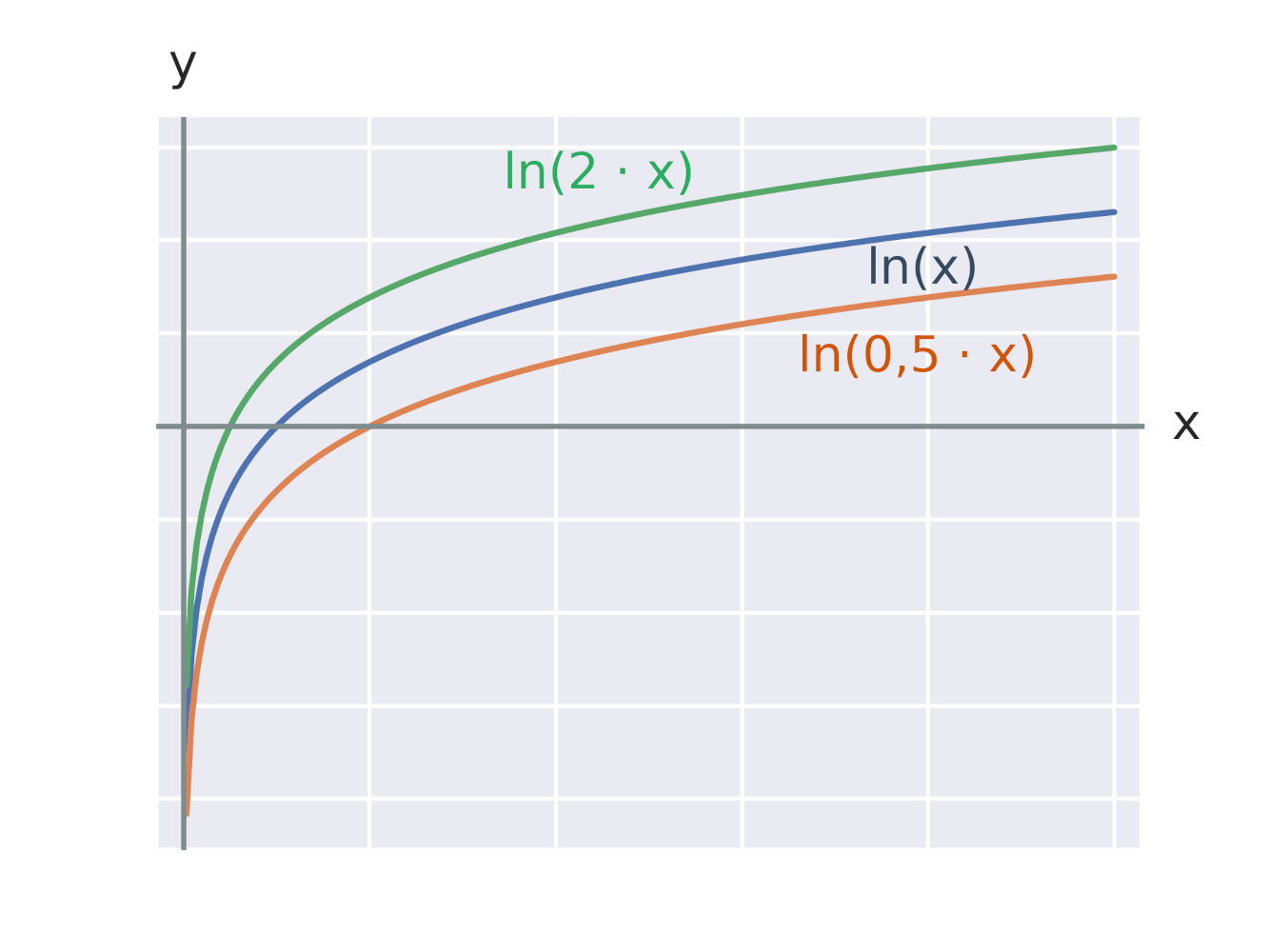
Grafy logaritmických funkcií
Logaritmická funkcia je inverzná k exponenciálnej funkcii s rovnakým základom. Grafy dvoch navzájom inverzných funkcií sú osovo súmerné podľa osi prvého kvadrantu (teda priamky spĺňajúcej x=y).

Graf každej logaritmickej funkcie tvaru y=\log_a x prechádza bodom [1,0], pretože pre ľubovoľnú konštantu a platí: \log_a 1=0. Na obrázku vidíme grafy logaritmických funkcií s rôznymi základmi 2, e, 10.

Značenie niektorých význačných logaritmických funkcií:
| funkcia | popis | ďalšie možné značenia |
|---|---|---|
| \log_a x | všeobecne logaritmus x so základom a pre nejaké a >0, a\neq 1 | |
| \ln x | prirodzený logaritmus x, teda logaritmus x so základom e | v angl. textoch niekedy \log x |
| \log x | dekadický logaritmus x, teda logaritmus x so základom 10 | \log_{10}x |
| \log_2 x | binárny logaritmus x, teda logaritmus x so základom 2 | niekedy sa objavuje \mathrm{lb}\;x |
Efekt pripočítania konštanty k logaritmickej funkcii

Efekt pripočítania konštanty k argumentu logaritmickej funkcie

Efekt vynásobenia logaritmickej funkcie konštantou

Efekt vynásobenia argumentu logaritmickej funkcie konštantou

Grafy lineárnych nerovníc
Grafom funkcie danej predpisom y= ax+b je priamka. Množinou riešení lineárnej nerovnice budú všetky body [x,y] ležiace v polrovine s hraničnou priamkou y= ax+b. Môže nastať jedna zo štyroch možností:
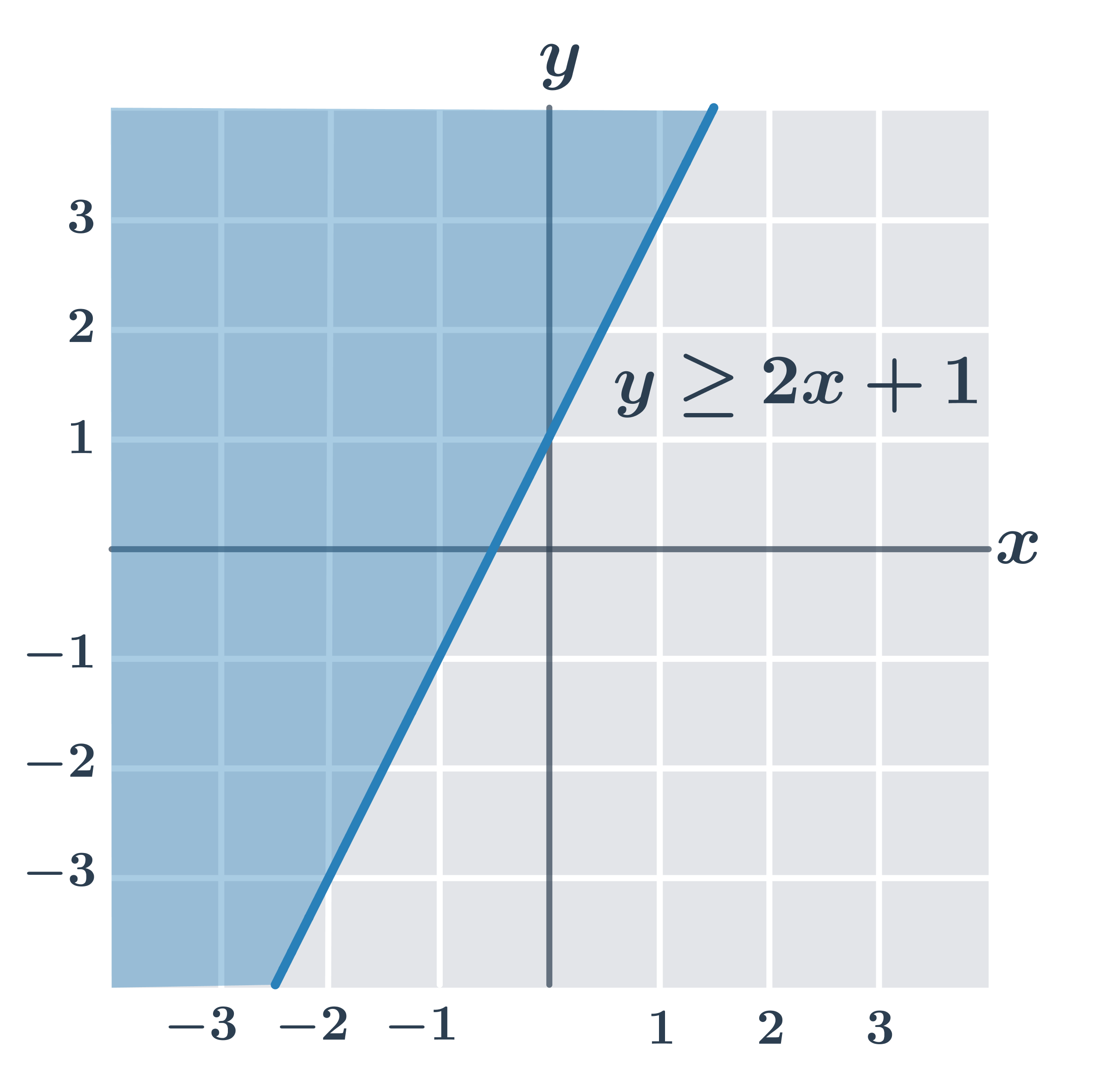
| y\geq ax+b | Nerovnosť spĺňajú všetky body v rovine, ktoré ležia priamo na priamke danej rovnicou y=ax+b alebo „nad“ touto priamkou (so súradnicou y väčšou než ax+b). |
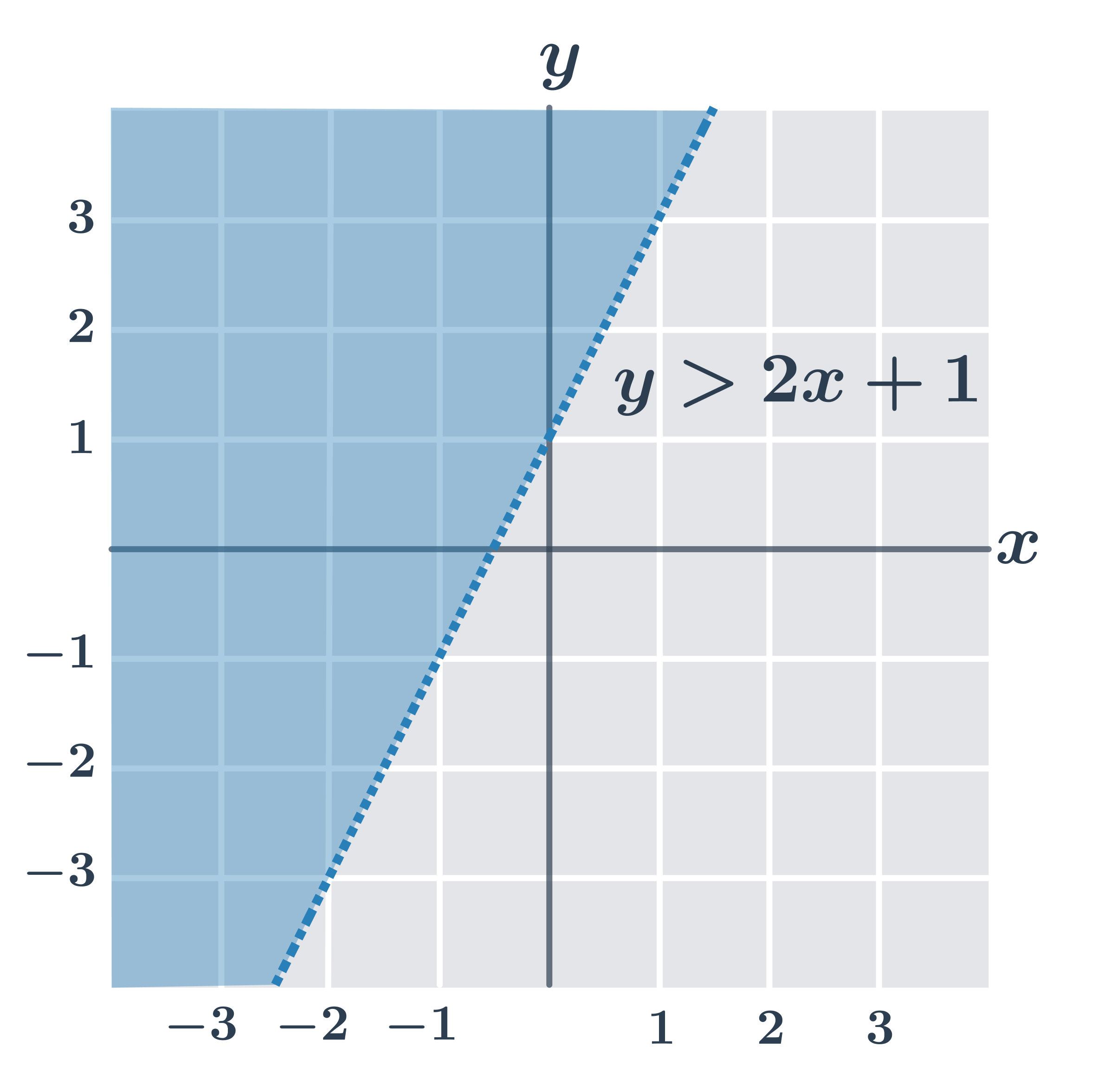
| y \gt ax+b | Nerovnosť spĺňajú všetky body v rovine, ktoré ležia „nad“ priamkou s rovnicou y=ax+b. |
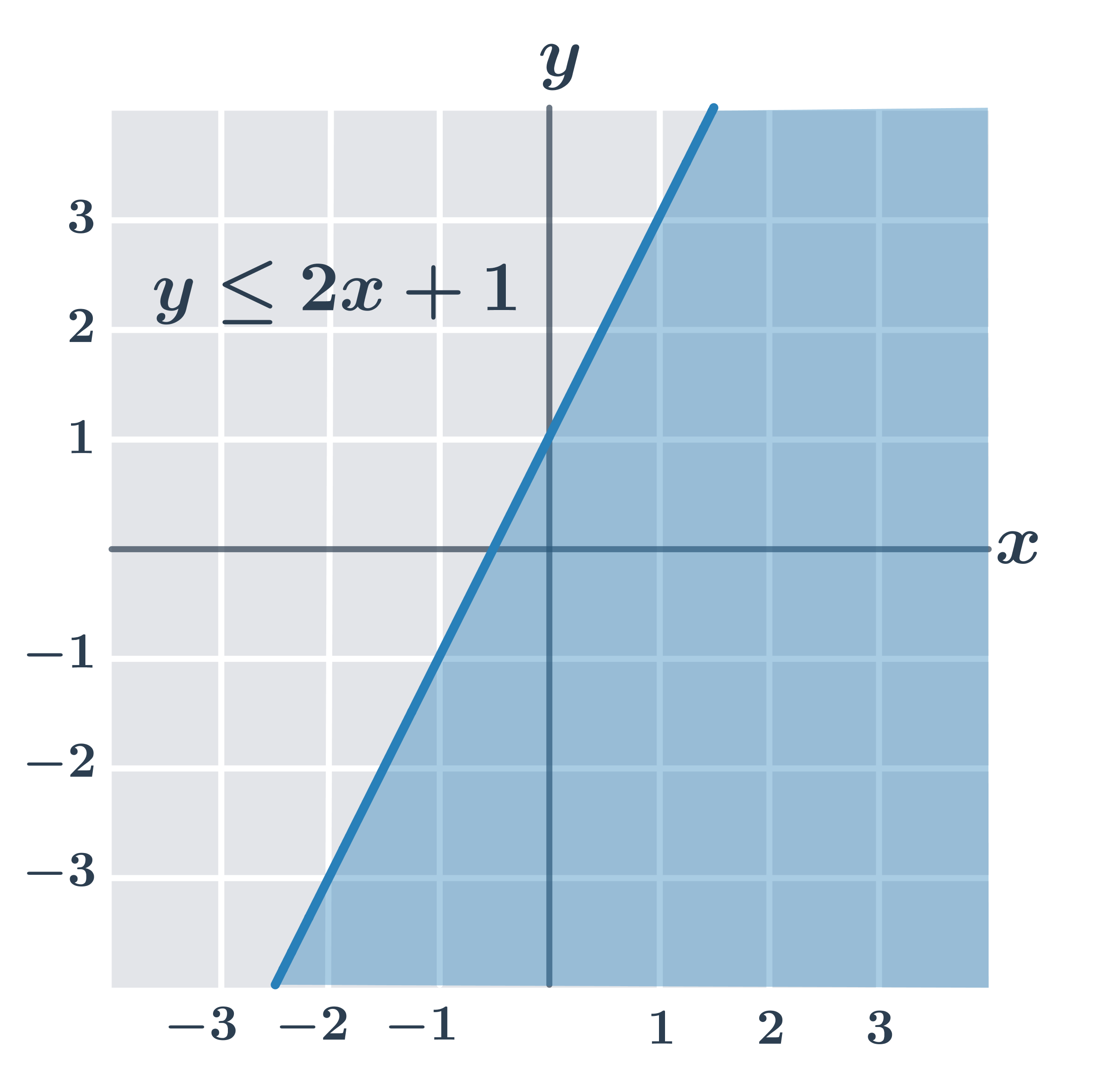
| y\leq ax+b | Nerovnosť spĺňajú všetky body v rovine, ktoré ležia na priamke s rovnici y=ax+b alebo „pod“ touto priamkou (so súradnicou y menšou než ax+b). |
| y \lt ax+b | Nerovnosť spĺňajú všetky body v rovine, ktoré ležia „pod“ priamkou s rovnicou y=ax+b. |
Na obrázkoch sú riešenia všetkých typov lineárnych nerovníc (všimnite si, že ak je v nerovnici iba znamienko \gt alebo \lt, body priamo na hraničnej priamke lineárnu nerovnicu nespĺňajú).
- y\geq 2x+1
- y \gt 2x+1
- y\leq 2x+1
- y \lt 2x+1
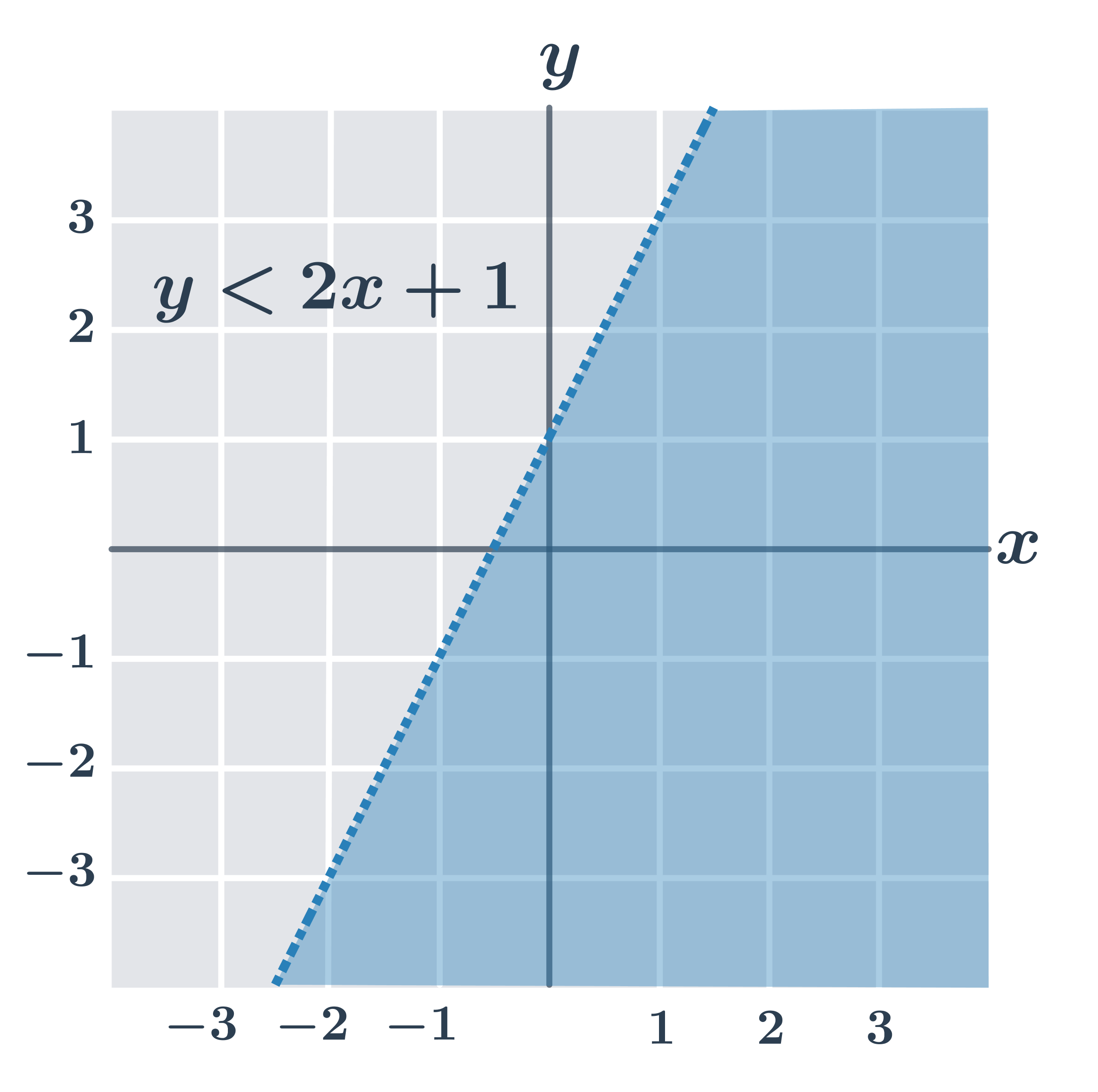
Lineárne funkcie
Funkcia f je lineárna, ak ju je možné vyjadriť v tvare f(x) = a\cdot x + b, kde a a b sú konštanty. Grafom lineárnej funkcie je priamka. Parameter a je smernica (tiež nazývaná sklon), parameter b určuje jej zvislý posun (tiež nazývaný absolútny člen).
Príklady lineárnych funkcií:
- f(x) = 2x
- f(x) = -4x+8
- f(x) = \frac13 x + 1{,2}
Aby bola funkcia lineárna, nemusí byť nutne priamo zapísaná v tvare f(x) = a\cdot x + b. Stačí, keď ide na tento tvar upraviť. Príklady:
- f(x) = 2-x môžeme prepísať ako f(x)= -1x + 2, čo je lineárna funkcia so smernicou -1 a absolútnym členom 2.
- f(x) = 5(3-x) môžeme prepísať ako f(x)= -5x + 15, čo je lineárna funkcia so smernicou -5 a absolútnym členom 15.
- f(x) = x^2 + 7 - x(x-1) vyzerá na prvý pohľad ako kvadratická funkcia, ale môžeme ju upraviť na f(x)= x + 7 (kvadratický člen sa vyruší), takže ide o lineárnu funkciu.
Vlastnosti lineárnej funkcie
Funkcia f je lineárna, ak ju je možné vyjadriť v tvare f(x) = a\cdot x + b, kde a a b sú konštanty. Definičný obor lineárnej funkcie je celá množina reálnych čísel.
Špeciálnym prípadom lineárnej funkcie je funkcia konštantná. Tú dostávame v prípade, že a=0.
Ak a \neq 0, potom pre lineárnu funkciu platí:
- je jednoduchá,
- nie je ohraničená zhora ani zdola,
- nemá maximum ani minimum,
- nie je periodická,
- obor hodnôt je množina reálnych čísel.
Pre a > 0 je funkcia f rastúca, pre a \lt 0 je funkcia f klesajúca.
Pre b=0 je funkcia f nepárna.
Grafom lineárnej funkcie je priamka. Priesečník grafu s osou y je v bode (0, b). Priesečník grafu s osou x je v bode (-\frac{b}{a}, 0).
HoreLineárne lomené funkcie
Lineárnu lomenú funkciu môžeme vyjadriť ako podiel dvoch lineárnych funkcií, teda v tvare
f:y =\frac{ax+b}{cx+d},
kde a,b,c,d sú konštanty.
Definičným oborom lineárnej lomené funkcie je množina všetkých reálnych čísel okrem hodnoty, v ktorej by bol menovateľ zlomku \frac{ax+b}{cx+d} nulový:
D(f)=\mathbb{R} - \{-\frac{d}{c}\}
Úpravou podmienky pre nenulovosť menovateľa zlomku dostaneme vyjadrenie definičného oboru pomocou nerovnice: cx+d\neq0\Rightarrow x\neq -\frac{d}{c}
Kedy je funkcia nelineárna a nekonštantná (a graf je hyperbola, nie priamka)
Na to, aby f:y=\frac{ax+b}{cx+d} nebola lineárna ani konštantná funkcia, musí byť splnených niekoľko podmienok. Pre konštanty a,b,c,d musí platiť: c\neq0 a bc-ad\neq0.
- pre c=0 by sme mali lineárnu funkciu danú rovnicou y =\frac{a}{d}\cdot x+\frac{b}{d}
- pre bc-ad=0 by sme mali konštantnú funkciu y =\frac{a}{c}
Vysvetlenie podmienky bc-ad\neq0
| Pre lineárnu lomenú funkciu danú predpisom \frac{ax+b}{cx+d} vykonáme delenie čitateľa zlomku \frac{ax+b}{cx+d} jeho menovateľom: |
| \begin{array}{lrrrr} \hspace{0.3cm}(\hspace{0.4cm}ax+\hspace{0.47cm}b)&:&(cx+d)&=&\frac{a}{c}\\\underline{-( \frac{a}{c}\cdot cx+\frac{a}{c}\cdot d)\hspace{0.5cm}}& \\ \hspace{1.05cm}0+b-\frac{a}{c}\cdot d\\ \end{array} |
| Vyšiel nám teda podiel \frac{a}{c} a zvyšok b-\frac{a}{c}\cdot d. |
| Ak by platilo b-\frac{a}{c}\cdot d=0, mohli by sme funkciu y =\frac{ax+b}{cx+d} zapísať zjednodušene v tvare y =\frac{a}{c} a to nie je lineárna lomená funkcia, ale konštantná funkcia. |
| Aby sme mali lineárnu lomenú funkciu, musí teda platiť b-\frac{a}{c}\cdot d\neq0. Túto podmienku môžeme vynásobením oboch strán hodnotou c upraviť na tvar: bc-ad\neq0 |
Špeciálnym prípadom lineárnej lomenej funkcie je nepriama úmernosť vyjadrená v tvare y =\frac{k}{x}.
HoreVlastnosti lineárnej lomenej funkcie
Lineárna lomená funkcia f:y =\frac{ax+b}{cx+d} má definičný obor D(f)=\R - \{-\frac{d}{c}\}, čo môžeme tiež zapísať ako zjednotenie dvoch intervalov: D(f)=(-\infty, -\frac{d}{c}) \cup (-\frac{d}{c}, \infty)
Ak c\neq0 a bc-ad\neq0, potom pre lineárnu lomenú funkciu platí:
- je prostá
- nie je periodická
- nemá maximum ani minimum
- nie je zhora ani zdola ohraničená
Ďalšie vlastnosti závisia od hodnôt koeficientov a, b, c, d:
- pre bc-ad \gt 0 je lineárna lomená funkcia klesajúca na intervale (-\infty, -\frac{d}{c}) a tiež klesajúca na intervale (-\frac{d}{c}, \infty)
- pre bc-ad \lt 0 je lineárna lomená funkcia rastúca na intervale (-\infty, -\frac{d}{c}) a tiež je rastúca na intervale (-\frac{d}{c}, \infty)
- pre a=0 a d=0 má lineárna lomená funkcia tvar: f:y =\frac{b}{cx} a je to nepárna funkcia (f(x) = - f(-x))
Príklad: vlastnosti funkcie f:y =\frac{3x+1}{4x+2}
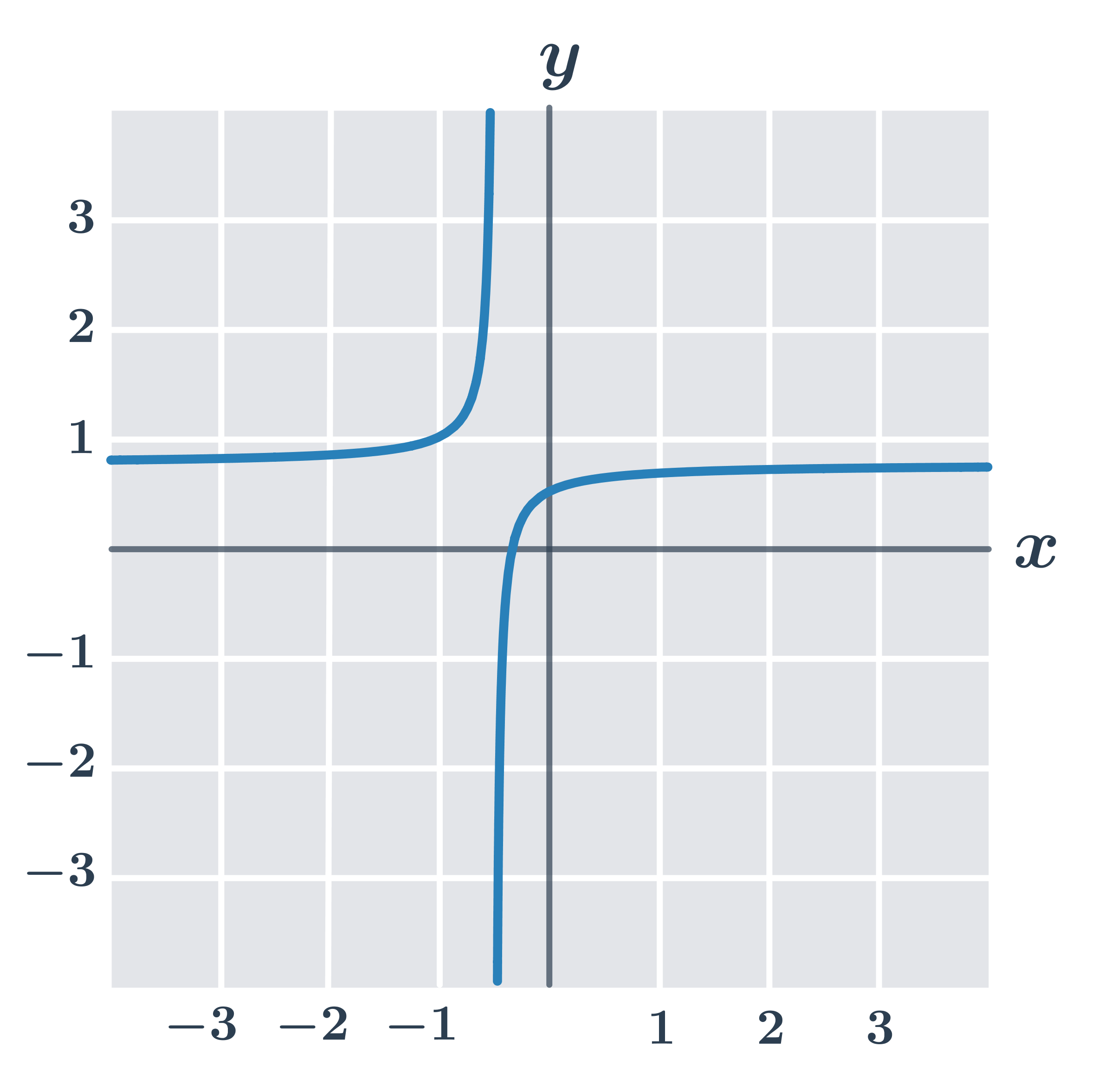
- Definičný obor D(f)=\R - \{-\frac{1}{2}\}.
- Funkcia je prostá.
- Funkcia je rastúca na intervale (-\infty,-\frac{1}{2}) a tiež je rastúca na intervale (-\frac{1}{2},\infty) – ľahko poznáme z grafu, ale zároveň môžeme overiť splnenie podmienky bc-ad \lt 0: pre danú funkciu bc-ad=1\cdot4-3\cdot2=-2.
Príklad: vlastnosti funkcie f:y =\frac{3}{2x}
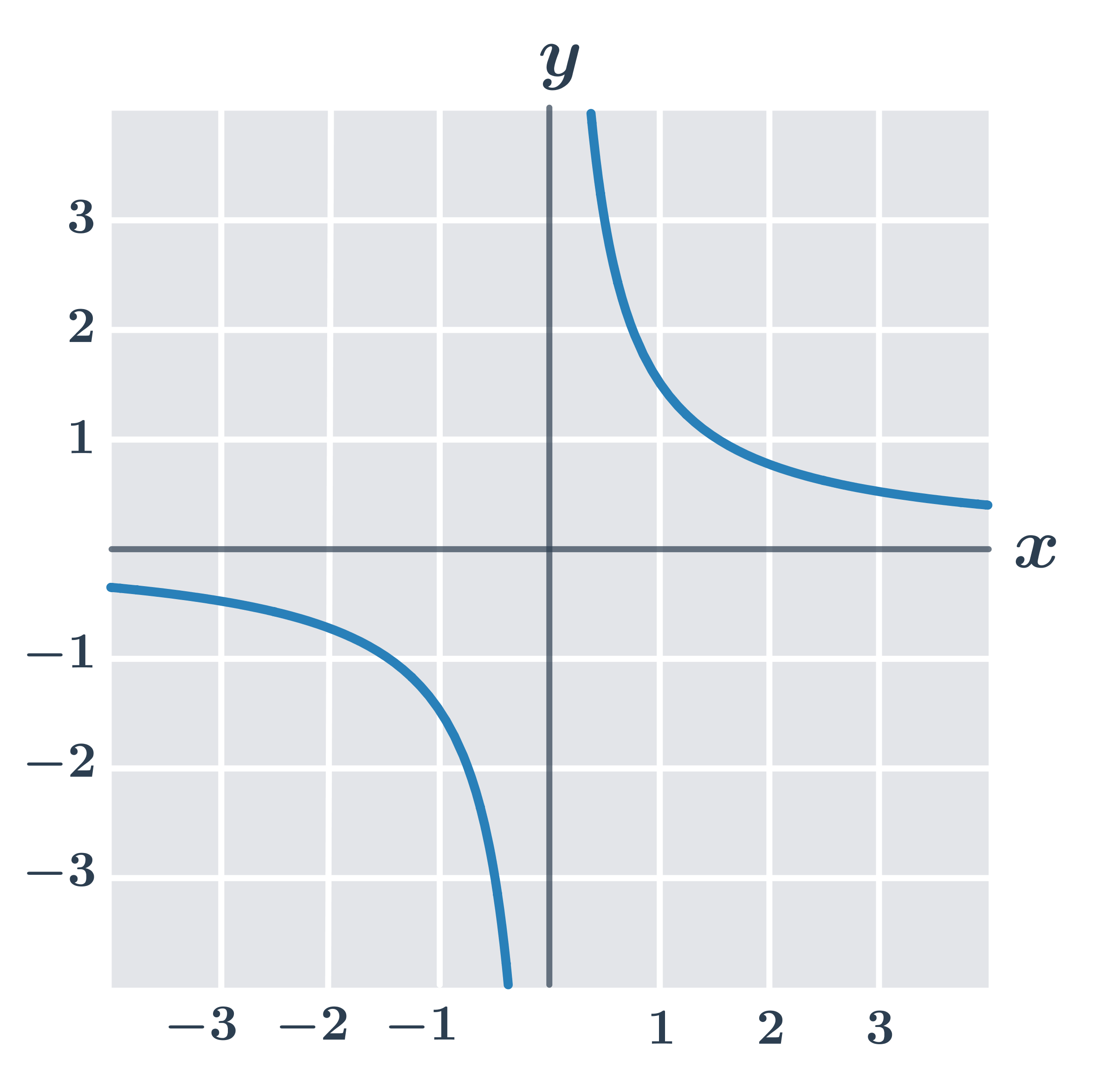
- Definičný obor D(f)=\R - \{0\}.
- Funkcia je prostá.
- Funkcia je klesajúca na intervale (-\infty,0) a tiež je klesajúca na intervale (0,\infty).
- Funkcia je nepárna – graf je súmerný podľa počiatku (pre lineárne lomené funkcie, kde a=0 a d=0).
Poznámka: ohraničenosť lineárnej lomenej funkcie
- Definičný obor lineárnej lomenej funkcie tvoria vždy dva intervaly.
- Ak si budeme všímať vlastnosti funkcie iba na jednom z týchto intervalov, ide o funkciu ohraničenú zdola alebo zhora. Napríklad funkcia na obrázku f:y =\frac{2x+3}{x+1}:

- Definičný obor D(f)=\R - \{-1\}, teda intervaly (-\infty;-1) a (-1;\infty).
- Na intervale (-\infty;-1) je funkcia ohraničená zhora a na intervale (-1;\infty) ohraničená zdola.
Kvadratické funkcie
Funkcia je kvadratická, keď ju môžeme vyjadriť v tvare f(x) = ax^2 + bx + c, kde a\neq 0. Funkcia je rýdzo kvadratická, ak nemá lineárny člen (teda b=0). Grafom kvadratickej funkcie je parabola. Kvadratická funkcia je špeciálny príklad polynómu (mnohočlena).
Príklady kvadratických funkcií:
- f(x) = x^2
- f(x) = (x+1)^2 = x^2 + 2x + 1
- f(x) = -3x^2 + 2x -8
Vlastnosti kvadratickej funkcie
Funkcia je kvadratická, ak ju je možné vyjadriť v tvare f(x) = ax^2 + bx + c, kde a\neq 0.
Definičný obor kvadratickej funkcie je celá množina reálnych čísel.
Kvadratická funkcia nemá žiadnu z nasledujúcich vlastností: jednoduchá, periodická, rastúca, klesajúca.
Ďalšie vlastnosti závisia od toho, či je kvadratický člen kladný alebo záporný:
- Pre a > 0 je funkcia zdola ohraničená, zhora nie je. V bode -\frac{b}{2a} má minimum.
- Pre a \lt 0 je funkcia zhora ohraničená, zdola nie je. V bode -\frac{b}{2a} má maximum.
Goniometrické funkcie
Goniometrické funkcie (alebo tiež trigonometrické funkcie) sú funkcie, ktoré dávajú do vzťahu uhol v pravouhlom trojuholníku a pomer dvoch jeho strán. Goniometrické funkcie majú široké využitie v geometrii a veľa praktických aplikácií (napríklad v navigácii, nebeskej mechanike či geodézii). Goniometrické funkcie súvisia nie len s geometriou, ale aj s mnohými inými oblasťami matematiky. Môžeme sa s nimi stretnúť napríklad v prípade komplexných čísel či nekonečných radov.
Základné goniometrické funkcie sú sínus, kosínus a tangens. Ďalšie sú potom sekans, kosekans a kotangens.
Inverzné funkcie k funkciám goniometrickým sa nazývajú cyklometrické (napr.arkussínus, arkustangens).
HoreGoniometrické funkcie a pravouhlý trojuholník
Goniometrické funkcie môžeme v pravouhlom trojuholníku vyjadriť nasledovne:
- Sínus (\sin) uhla \alpha je pomer dĺžky odvesny protiľahlej uhlu \alpha a dĺžky prepony.
- Kosínus (\cos) uhla \alpha je pomer dĺžky odvesny priľahlej uhlu \alpha a dĺžky prepony.
- Tangens (\tan) uhla \alpha je pomer dĺžky odvesny protiľahlej uhlu \alpha a dĺžky odvesny priľahlej uhlu \alpha.
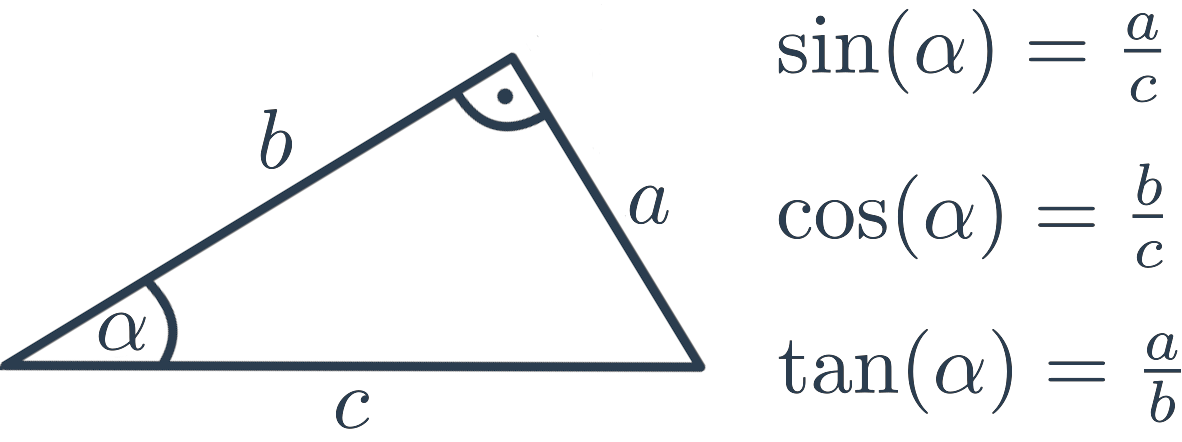
Hodnoty goniometrických funkcií
Často používané hodnoty goniometrických funkcií ilustruje tento obrázok jednotkovej kružnice – x-ová súradnica bodu zodpovedá hodnote \cos daného uhla, y-ová súradnica bodu zodpovedá hodnote \sin daného uhla.
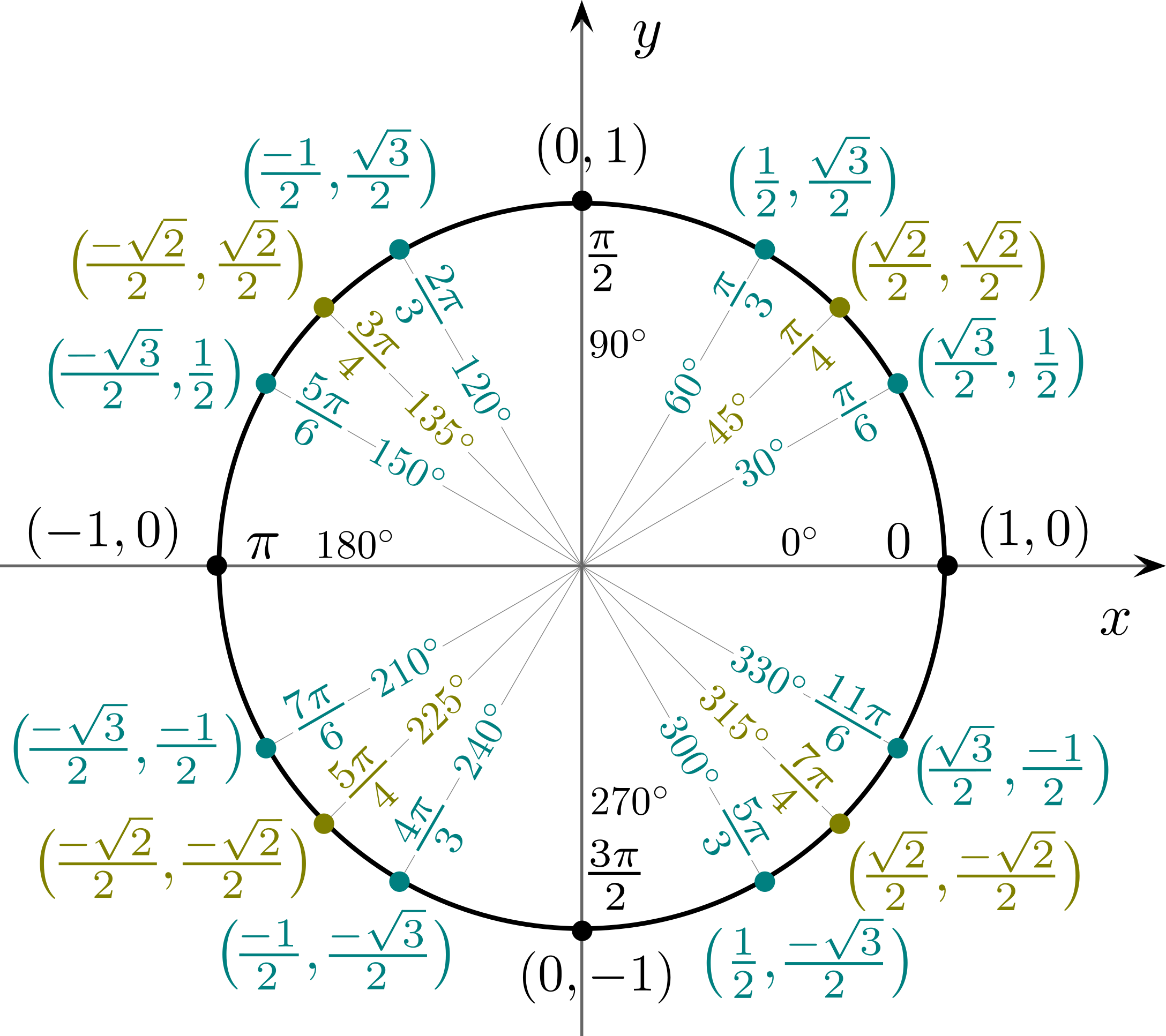
Goniometrické funkcie: vzťahy a vzorce
Pre goniometrické funkcie platí celý rad vzťahov a vzorcov. Výber tých základných:
- Záporné hodnoty uhlov:
- \sin(-x) = -\sin(x) (nepárna funkcia)
- \cos(-x) = \cos(x) (párna funkcia)
- \tan(-x) = -\tan(x) (nepárna funkcia)
- Posuny:
- \sin(x+2\pi) = \sin(x) (perióda 2\pi)
- \sin(x+\pi) = -\sin(x)
- \sin(x+\frac{\pi}{2}) = \cos(x)
- Súčtové vzorce goniometrických funkcií:
- \sin(x+y) = \sin(x)\cos(y)+\cos(x)\sin(y)
- \sin(x-y) = \sin(x)\cos(y)-\cos(x)\sin(y)
- \cos(x+y) = \cos(x)\cos(y)-\sin(x)\sin(y)
- \cos(x-y) = \cos(x)\cos(y)+\sin(x)\sin(y)
- Dvojnásobný argument:
- \sin(2x) = 2\sin(x)\cos(x)
- \cos(2x) = \cos^2(x)-\sin^2(x)
- \tan(2x) = \frac{2\tan(x)}{1-\tan^2(x)}
Vlastnosti goniometrických funkcií
Pre obe funkcie \sin(x) a \cos(x) platí:
- definičný obor je množina reálnych čísel,
- obor hodnôt je interval \langle -1, 1 \rangle,
- funkcia je ohraničená,
- funkcia je periodická s periódou 2\pi,
- funkcia nie je prostá.
Pre funkciu \sin(x) platí:
- je nepárna,
- nulové hodnoty nadobúda v bodoch x=k\pi.
Pre funkciu \cos(x) platí:
- je párna,
- nulové hodnoty nadobúda v bodoch x=(2k+1)\frac{\pi}{2}.
Pre funkciu \tan(x) platí:
- definičný obor je \{x \in \mathbb{R}: x \neq (2k+1)\frac{\pi}{2} \},
- obor hodnôt je množina reálnych čísel,
- funkcia je nepárna,
- funkcia je periodická s periódou \pi,
- funkcia je ohraničená,
- nulové hodnoty nadobúda v bodoch x=k\pi.
Mocninové funkcie
Funkcia je mocninová, ak ju je možné vyjadriť v tvare y= x^k, kde k je konštanta. Definičný obor aj vlastnosti funkcie sú dané hodnotou konštanty k.
Medzi najčastejšie typy mocninových funkcií (pre koeficient n\in \N) patria:
- y= x^n … napríklad: y= x^2, y= x^3
- y= x^{-n} … napríklad: y=x^{-2} (môžeme tiež písať v tvare: y= \frac{1}{x^2})
- y= x^{\frac{1}{n}} … napríklad: y= x^{\frac{1}{3}} (môžeme tiež písať v tvare: y= \sqrt [3]{x})
Exponenciálne funkcie
Funkcia je exponenciálna iba vtedy, keď ju je možné vyjadriť v tvare y= a^x, kde a je konštanta. Konštanta a sa nazýva základ a môže to byť akékoľvek kladné reálne číslo okrem hodnoty 1, teda a\in (0,1)\cup (1,\infty). Výraz x je exponent. Definičným oborom exponenciálnej funkcie je množina všetkých reálnych čísel, oborom hodnôt je množina všetkých kladných reálnych čísel. V bežnej reči používame pojem exponenciálny rast, ak chceme povedať, že niečo veľmi rýchlo rastie, napríklad počty chorých pri epidémii.
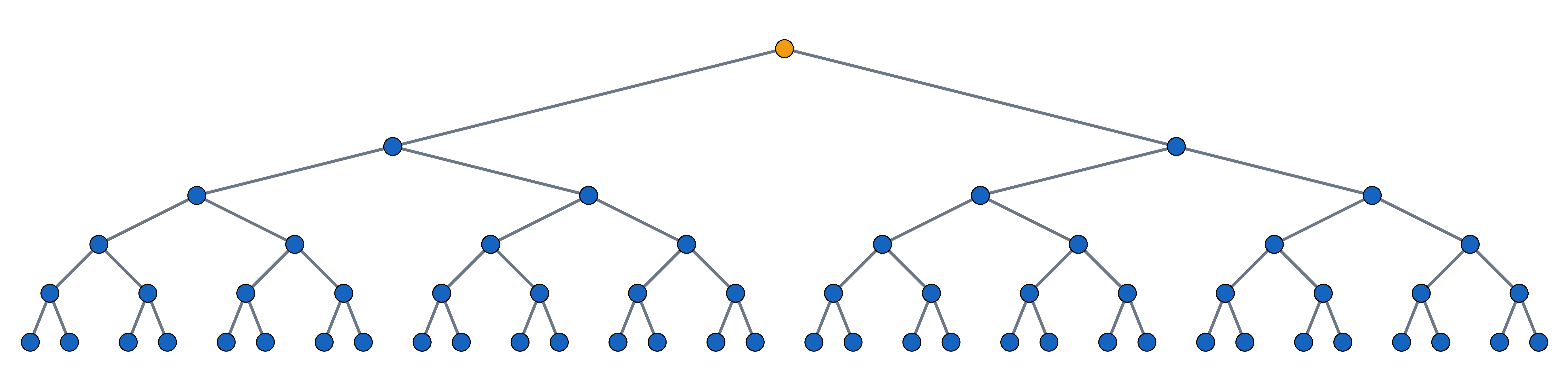
Príklad: exponenciálny rast
Nákazlivá choroba sa šíri exponenciálne. Ak si zoberieme exponenciálnu funkciu so základom a=2, znamená to, že každý chorý nakazí ďalších dvoch ľudí. Šírenie choroby sa dá dobre znázorniť obrázkom:
Vlastnosti exponenciálnych funkcií
Pre exponenciálnu funkciu f:y =a^x platí:
- definičný obor D(f)=\R
- obor hodnôt H(f)=(0, \infty)
- je prostá
- nie je periodická
- nie je párna ani nepárna
- nemá maximum ani minimum
- je zdola ohraničená
Ďalšie vlastnosti závisia od hodnoty koeficientu a:
- pre a>1 je exponenciálna funkcia rastúca
- pre a\in (0,1) je exponenciálna funkcia klesajúca
Príklad: vlastnosti funkcie f\!: y =3^x
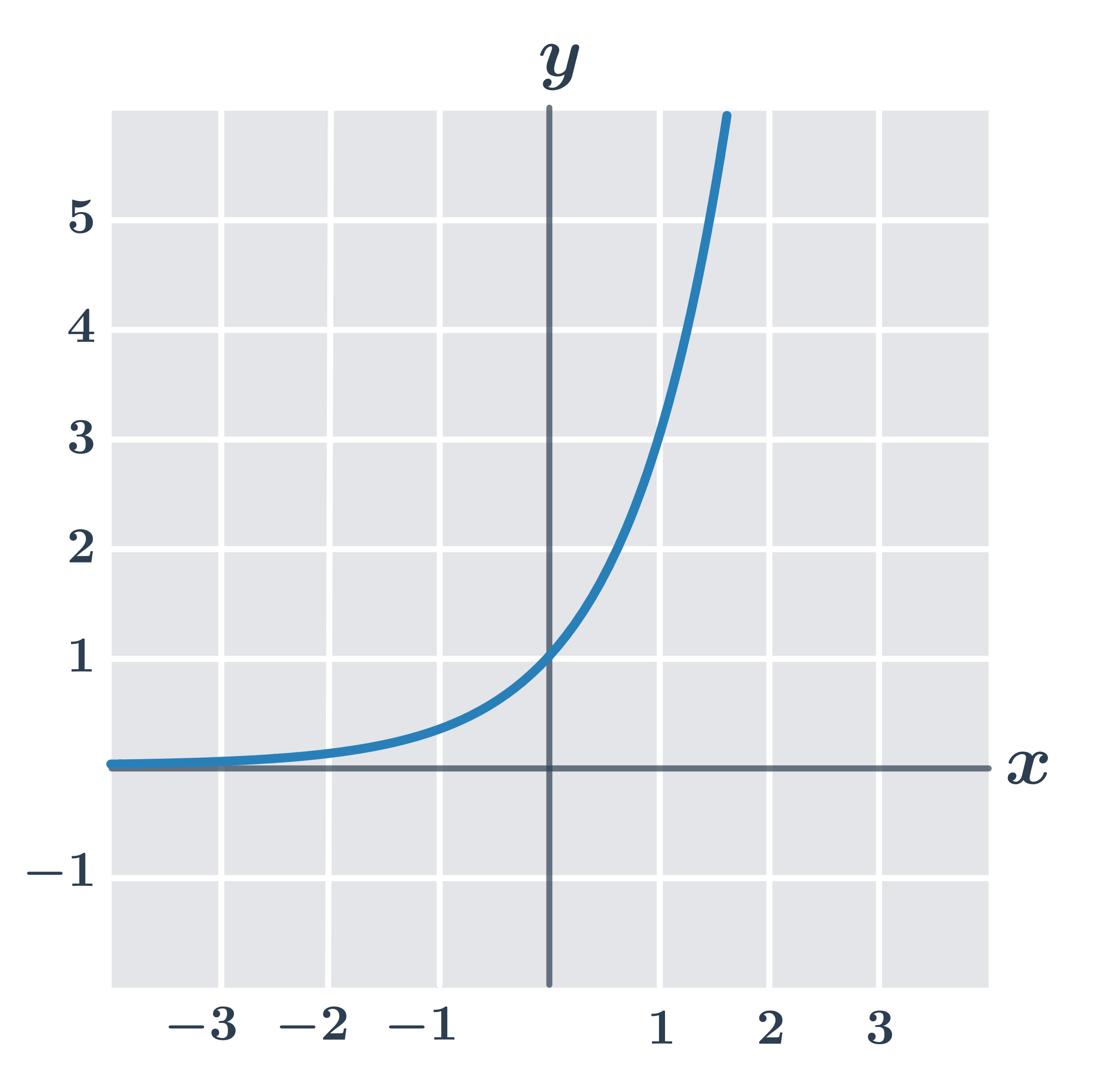
- definičný obor D(f)=\R
- obor hodnôt H(f)=(0, \infty)
- je prostá
- je zdola ohraničená
- je rastúca
Príklad: vlastnosti funkcie f\!: y=\left (\frac{1}{2}\right)^x
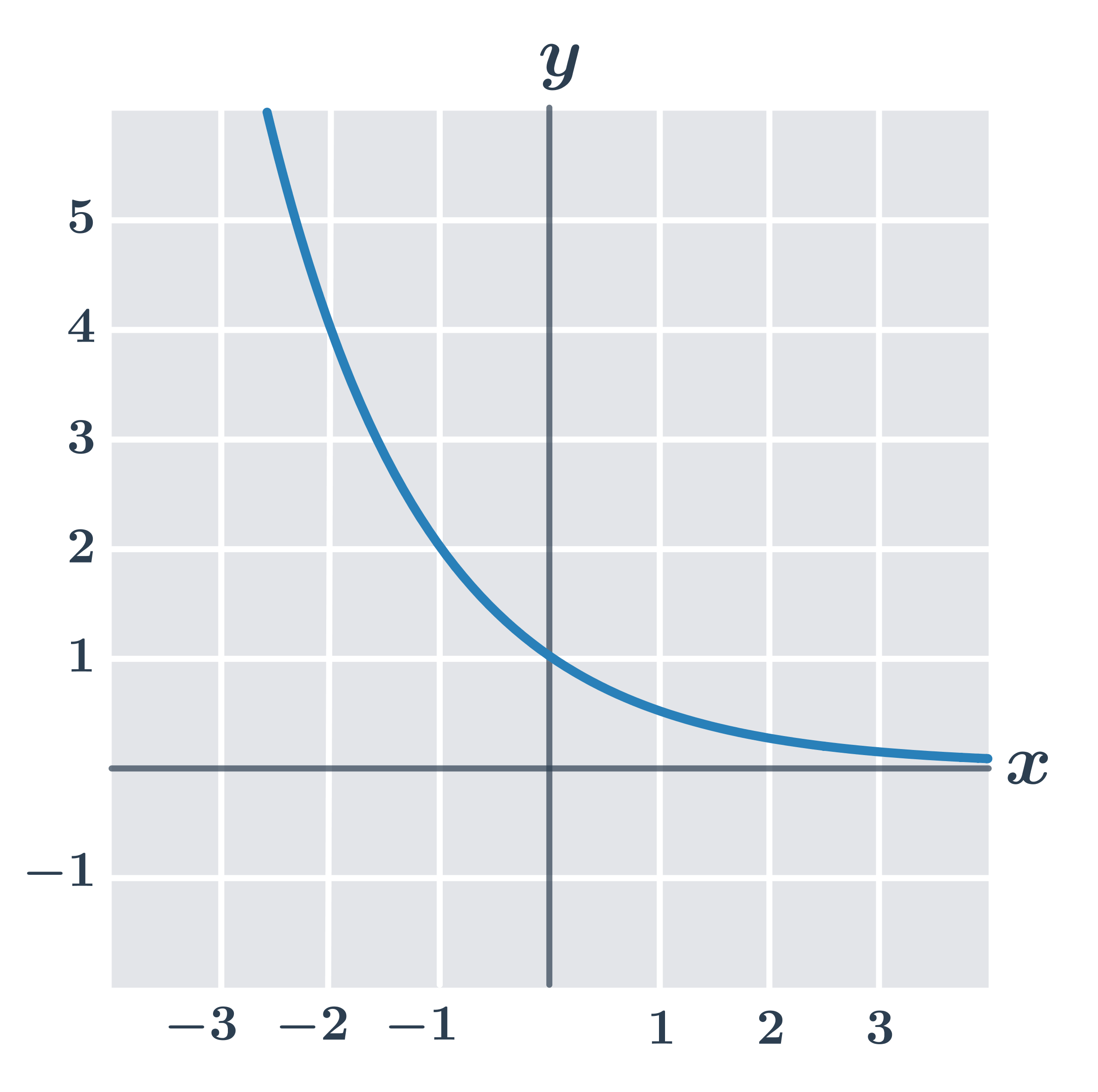
- definičný obor D(f)=\R
- obor hodnôt H(f)=(0, \infty)
- je prostá
- je zdola ohraničená
- je klesajúca
Logaritmické funkcie
Funkcia je logaritmická, ak ju je možné vyjadriť v tvare y=\log_a x, kde a je konštanta. Konštanta a sa nazýva základ a môže to byť akékoľvek kladné reálne číslo okrem hodnoty 1, teda a\in (0,1)\cup (1,\infty). Výraz x je argument.
Definičným oborom logaritmickej funkcie je množina všetkých kladných reálnych čísel, oborom hodnôt je množina všetkých reálnych čísel.
HoreVlastnosti logaritmických funkcií
Pre logaritmickú funkciu y=\log_ax platí:
- definičný obor D(f)=(0, \infty)
- obor hodnôt H(f)=\R
- je prostá
- nie je periodická
- nie je párna ani nepárna
- nemá maximum ani minimum
- nie je ohraničená
Ďalšie vlastnosti závisia od hodnoty koeficientu a:
- pre a>1 je logaritmická funkcia rastúca
- pre a\in (0,1) je logaritmická funkcia klesajúca
Príklad: vlastnosti funkcie y=\log_2 x
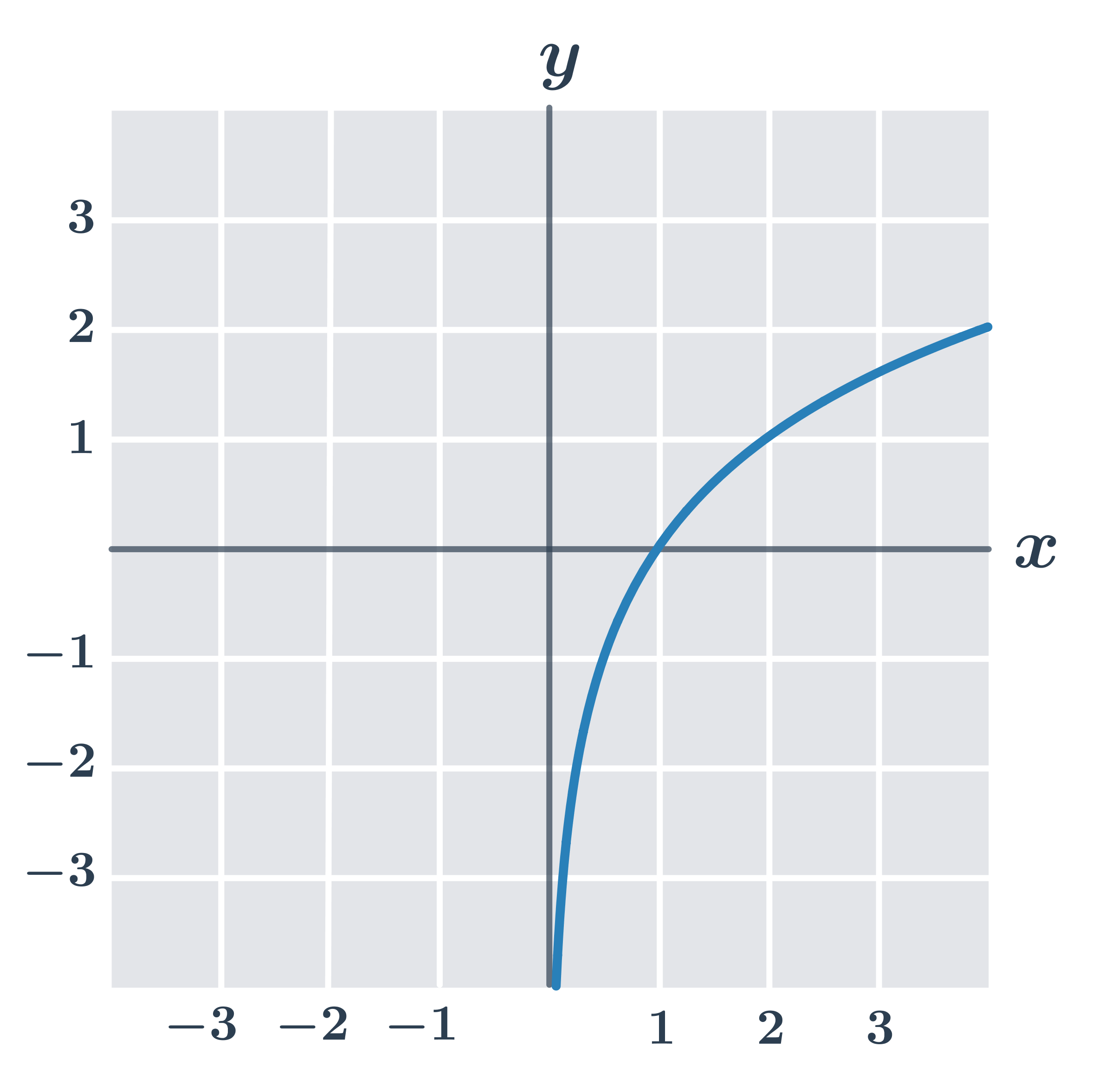
- definičný obor D(f)=(0, \infty)
- obor hodnôt H(f)=\R
- je prostá
- je rastúca
Príklad: vlastnosti funkcie y=\log_{\frac{1}{2}} x
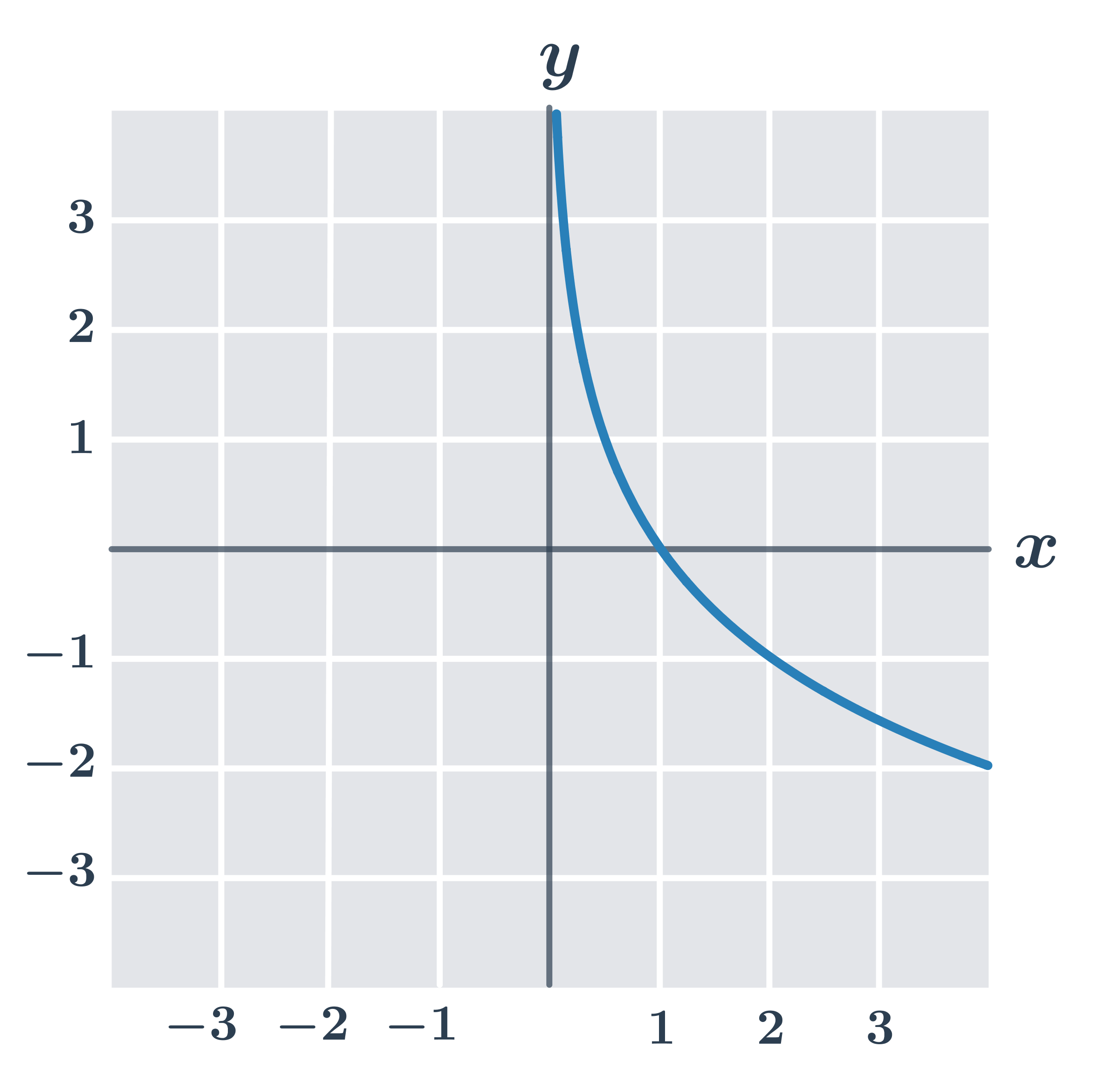
- definičný obor D(f)=(0, \infty)
- obor hodnôt H(f)=\R
- je prostá
- je klesajúca
Príklad: vlastnosti funkcie y=\log_3 (x+2)
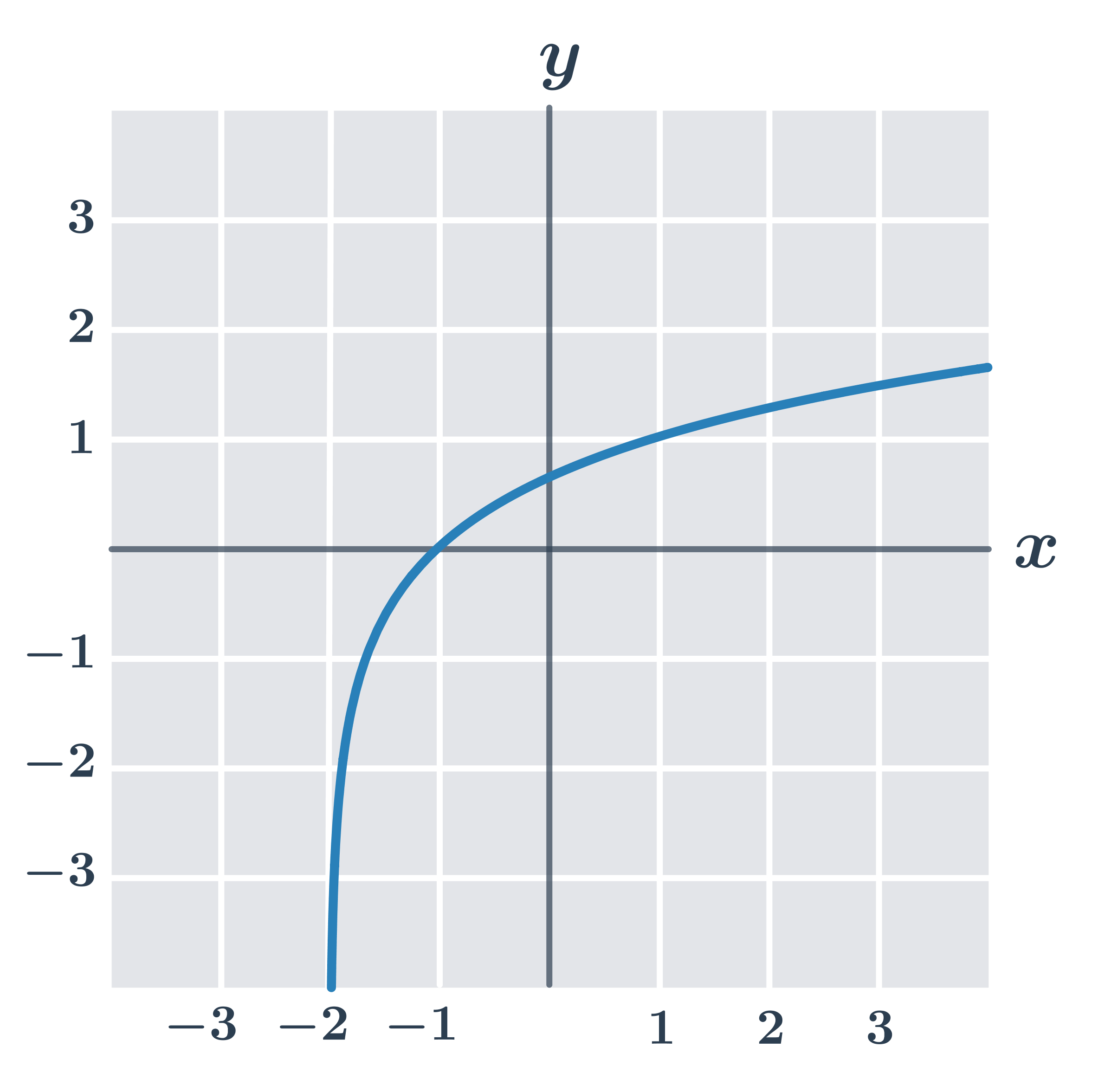
- definičný obor: D(f)=(-2, \infty) … výraz v logaritme musí byť kladný, teda musí platiť: x+2>0\Rightarrow x>-2
- obor hodnôt H(f)=\R
- je prostá
- je rastúca
- priesečník grafu s osou x je bod [-1,0] … nájdeme ako riešenie logaritmickej rovnice: 0=\log_3(x+2). Podľa pravidiel pre počítanie s logaritmami musí platiť: 3^0=x+2\Rightarrow 1=x+2\Rightarrow x=-1