Výpis prehľadov

Kužeľosečky

Prechádzate súhrny informácií k určitým témam. Systémy Vieme sa zameriavajú hlavne na ich precvičovanie. K cvičeniam k jednotlivým podtémam sa dostanete pomocou odkazov nižšie.

« Späť na precvičovanie

Podkapitoly

Kužeľosečky
Kružnica (kužeľosečka)
Elipsa
Parabola
Hyperbola

Kužeľosečky

Prejsť k cvičeniam s touto témou »

Ako už názov napovedá, majú kužeľosečky spoločný pôvod. Vzniknú ako rez rotačnej kužeľovej plochy rovinou.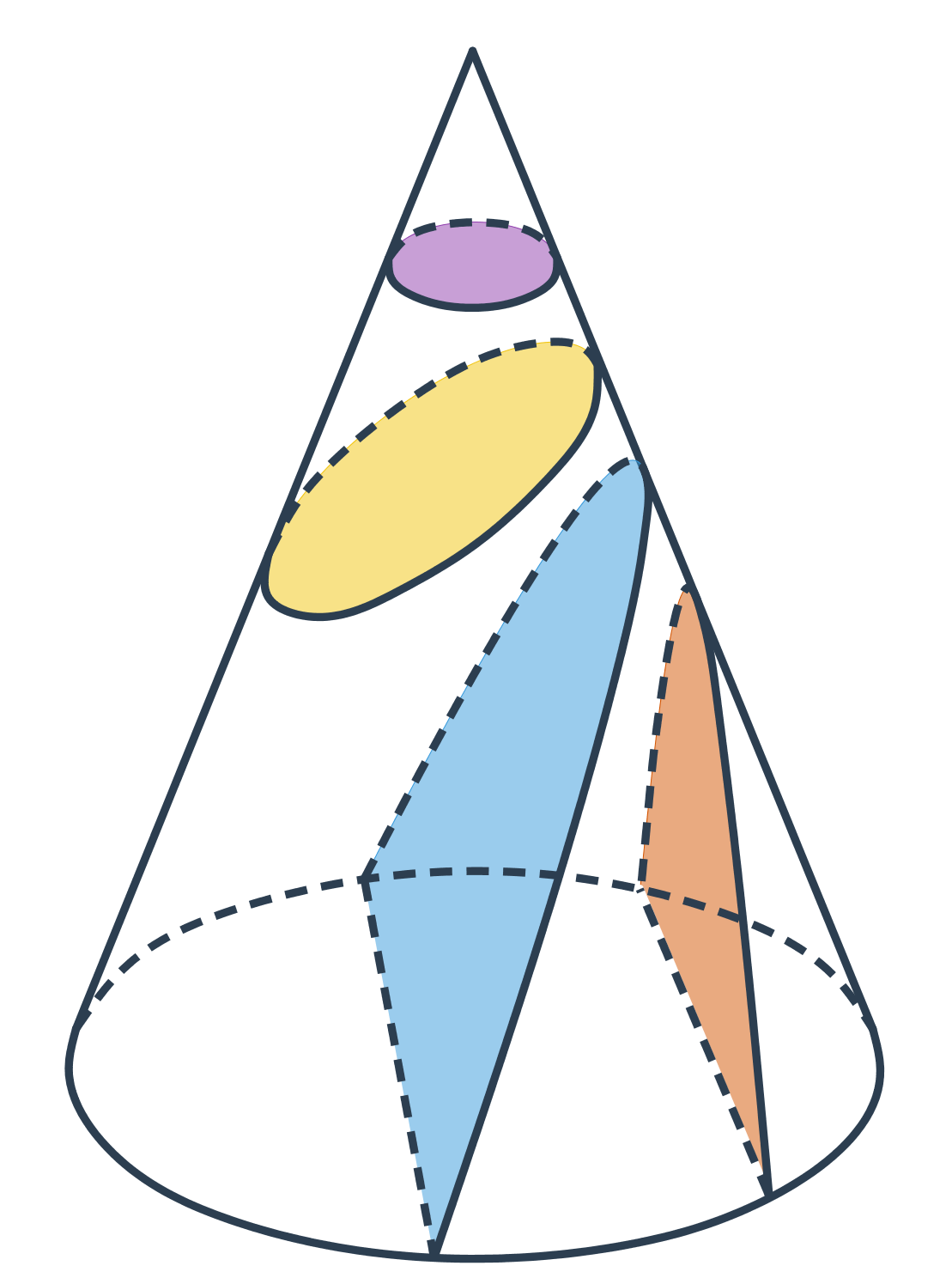

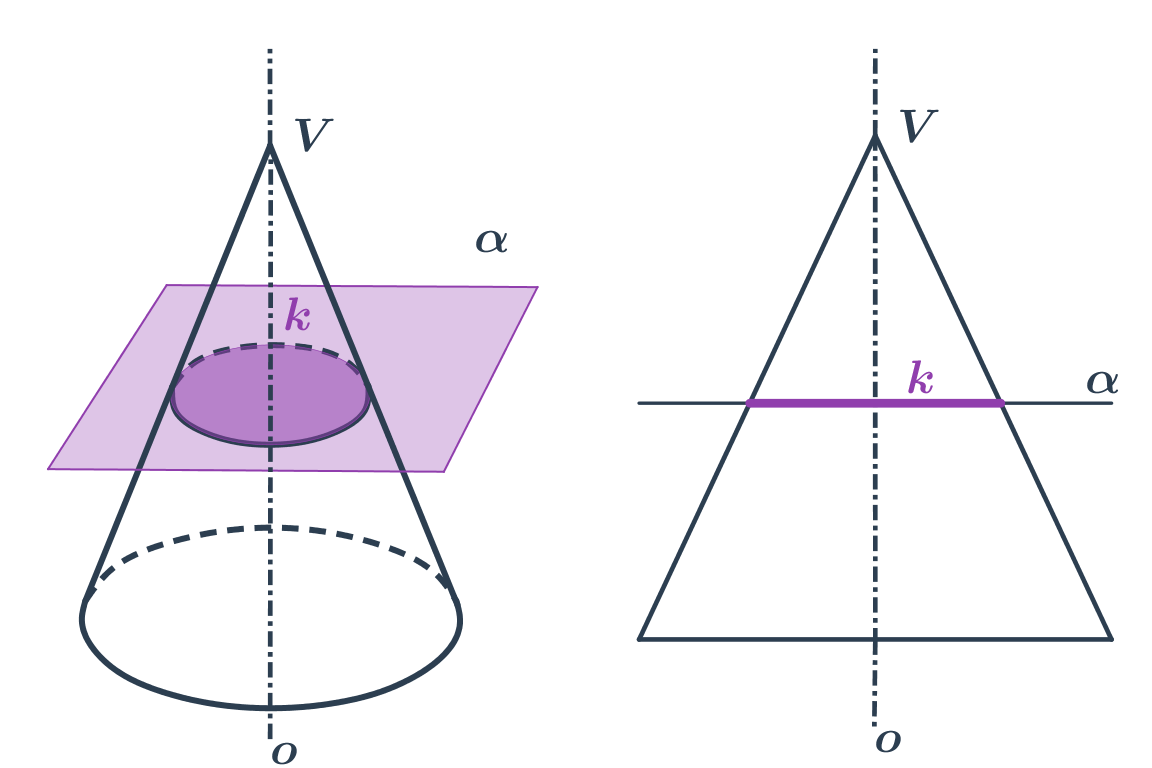
Kružnica vznikne rezom roviny kolmej na os kužeľovej plochy.
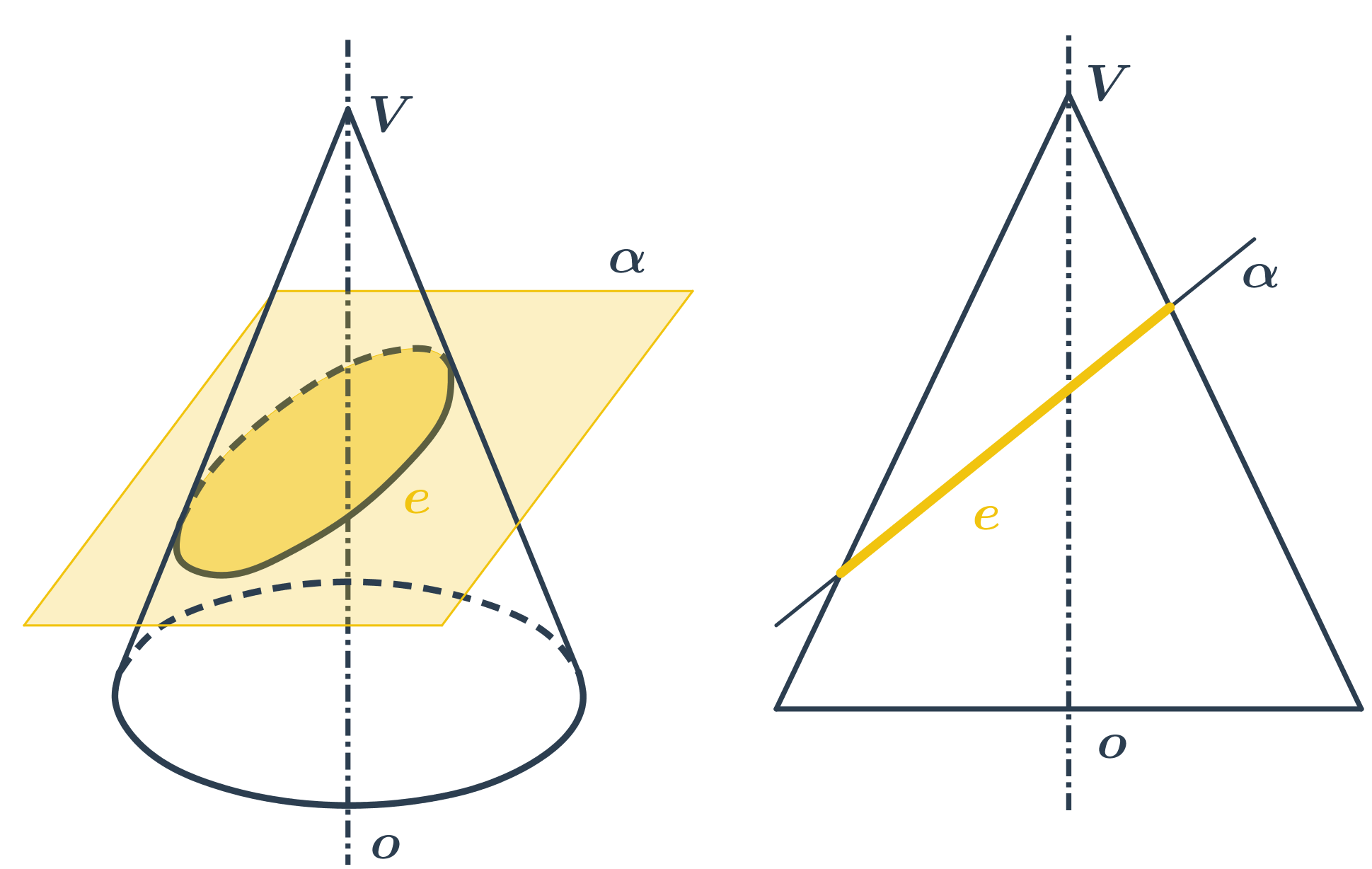
Ak rovinu rezu trochu nakloníme, vznikne elipsa.

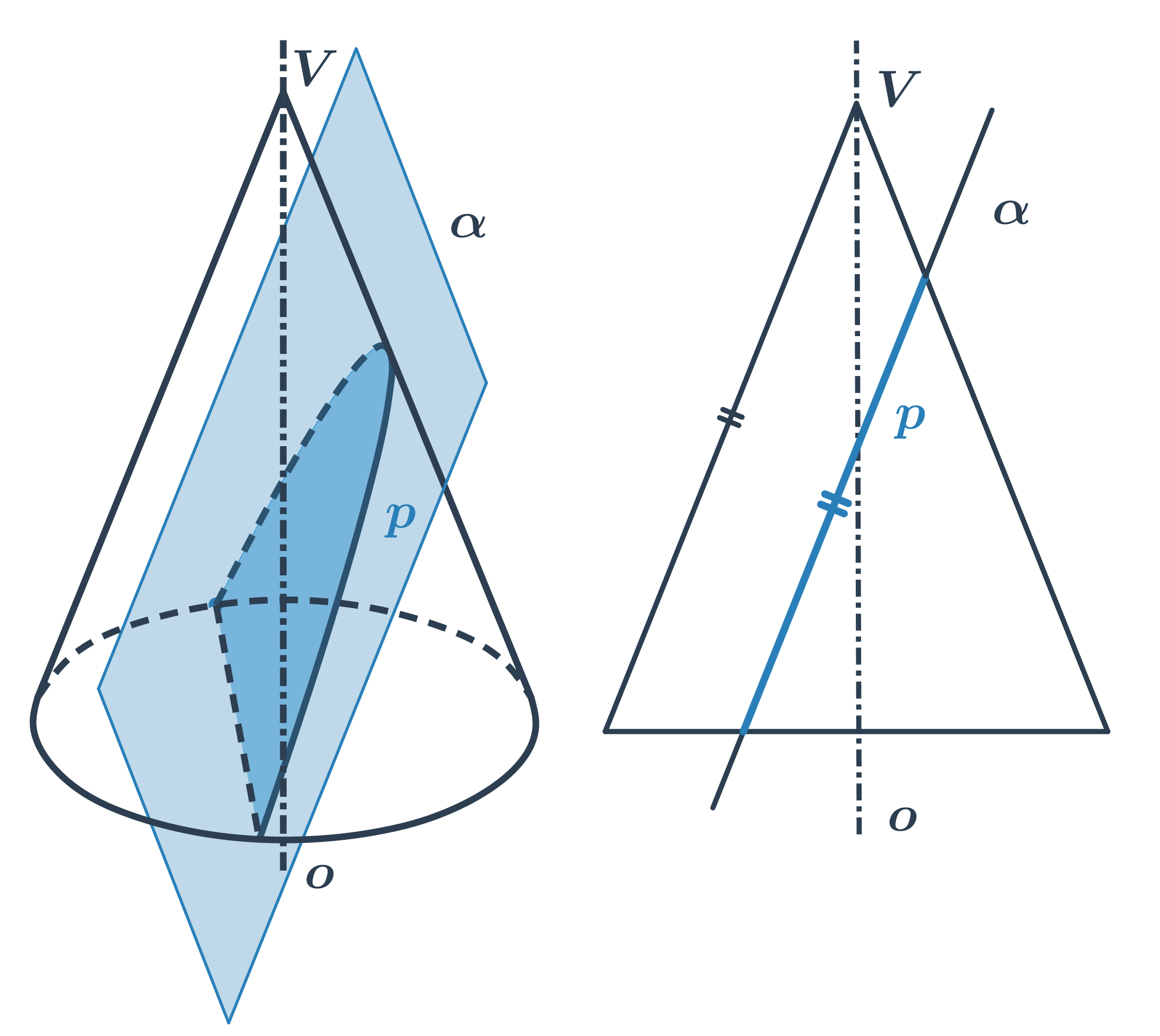
Ak rovinu rezu nakloníme toľko, že bude rovnobežná s niektorou z priamok na kužeľovej ploche, vznikne parabola.
Pri ďalšom nakláňaní už rovina rezu pretne obe časti kužeľovej plochy a vnikne dvojdielna hyperbola.

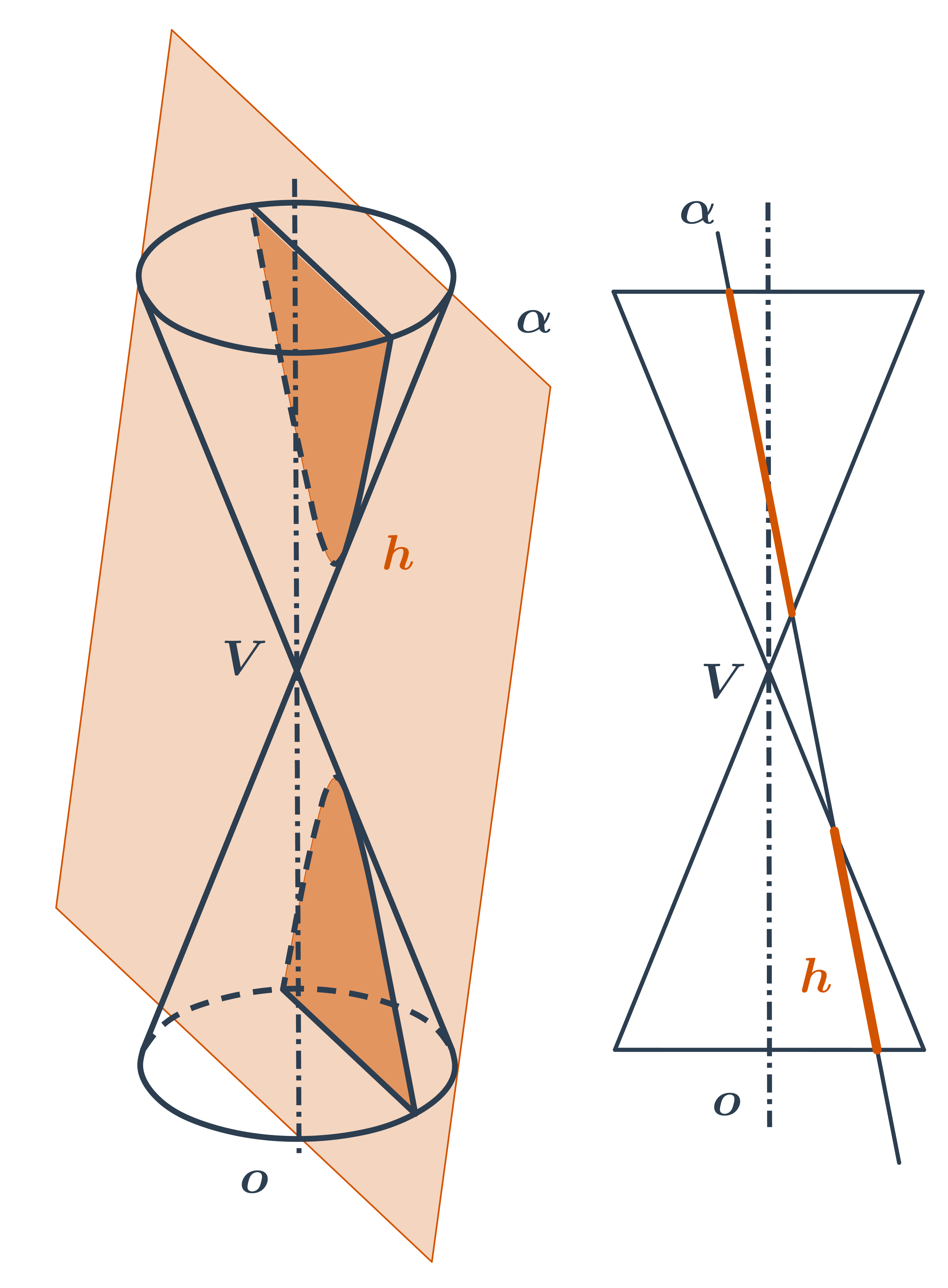
Kužeľosečky môžeme tiež chápať ako množiny bodov danej vlastnosti. V analytickej geometrii často zapisujeme tieto množiny pomocou rovníc.

Kružnica (kužeľosečka)

Prejsť k cvičeniam s touto témou »

Kružnica je množina všetkých bodov v rovine, ktoré majú od daného pevného bodu S rovnakú vzdialenosť r. Bod S nazývame stred kružnice, hodnotu r nazveme polomer kružnice.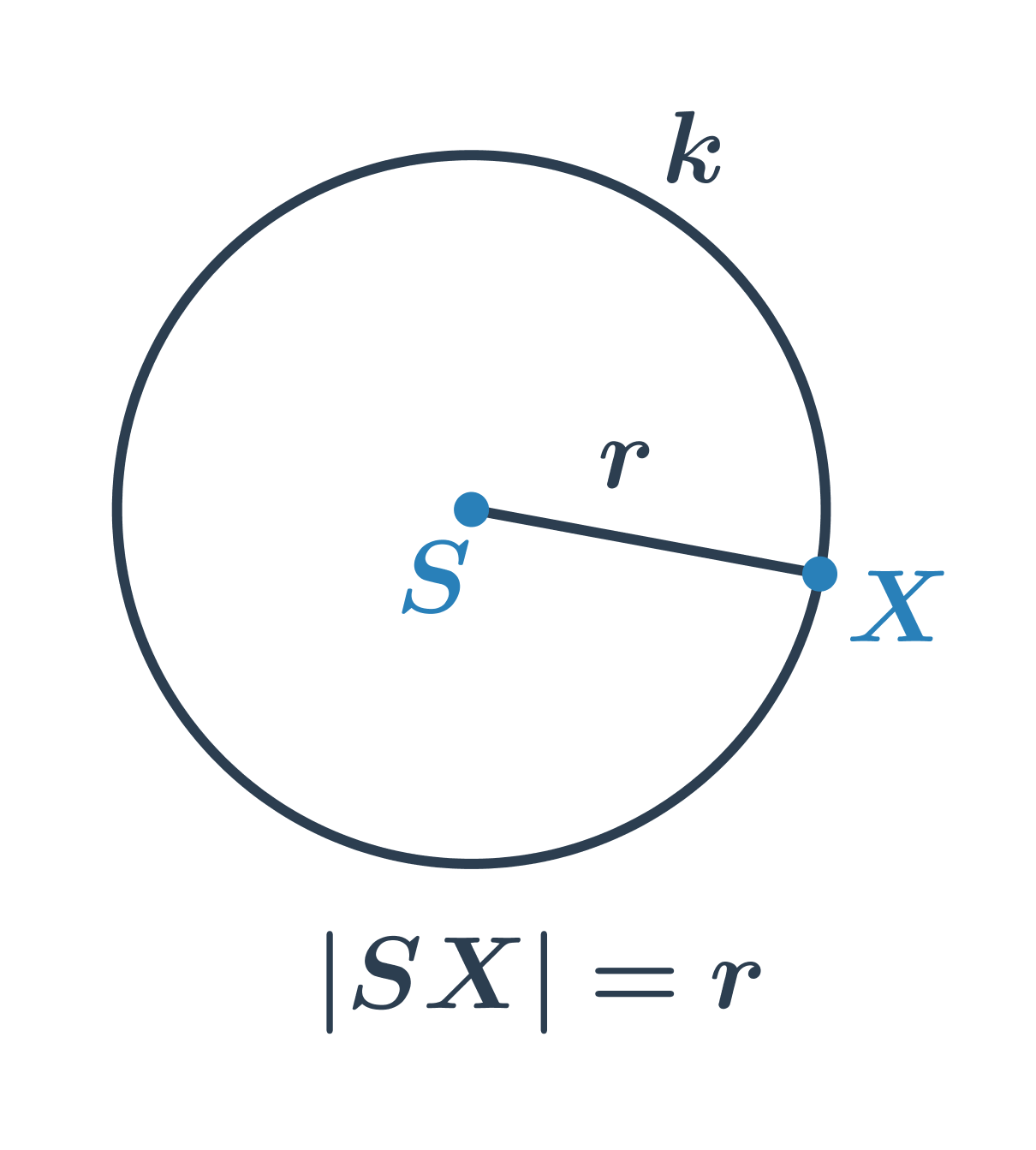

Stredová rovnica kružnice

Stredová rovnica kružnice so stredom S[m;n] a polomerom r je v tvare: (x-m)^2 +(y-n)^2=r^2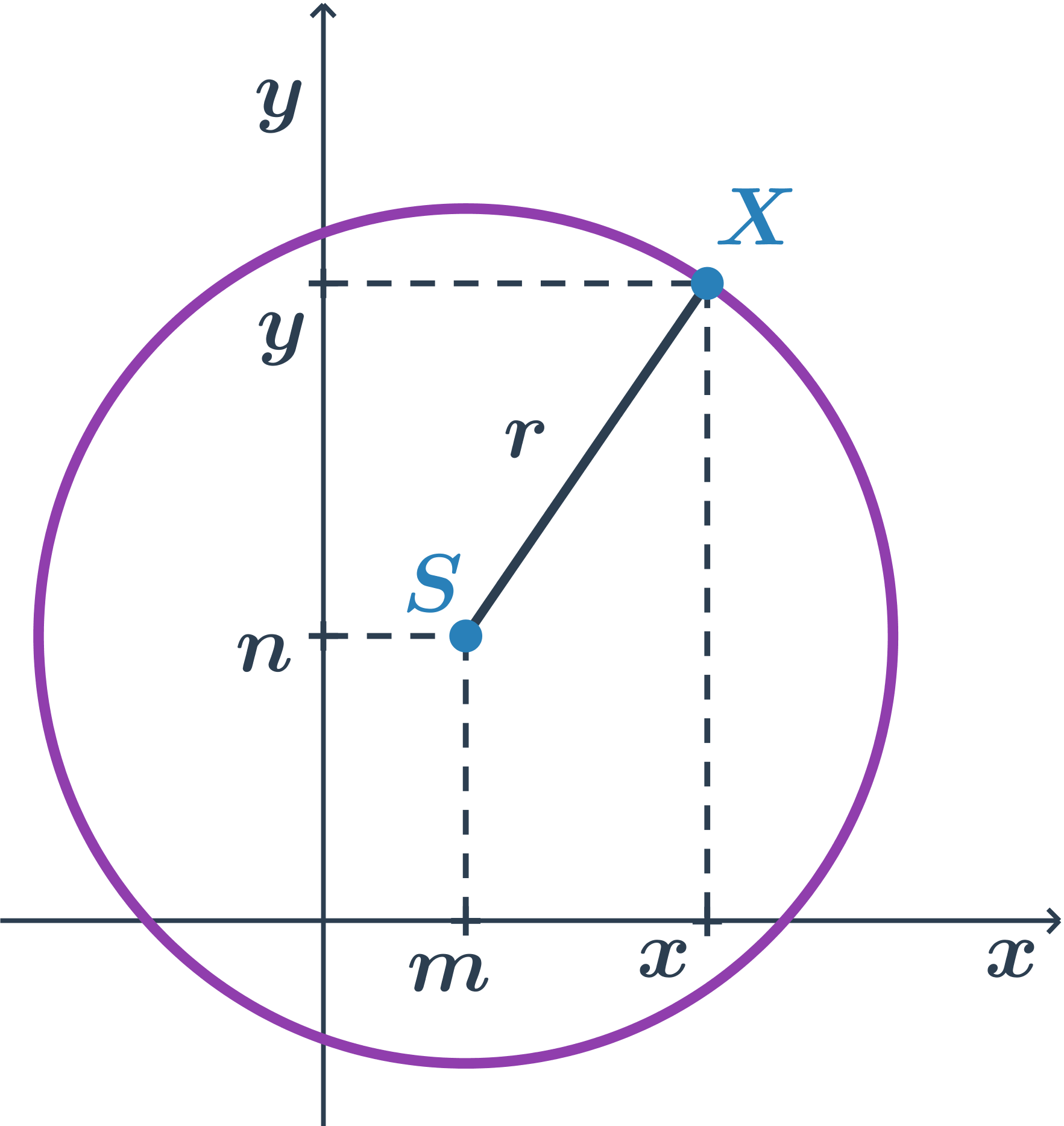

Príklad: Určite stredovú rovnicu kružnice so stredom v bode S[-1;2] a polomerom r=3.

Stredová rovnica je v tvare: (x-m)^2 +(y-n)^2=r^2
Dosadíme súradnice stredu a polomer. Pri dosadení si dáme pozor na to, že súradnice stredu v stredovej rovnici odčítame: (x-(-1))^2 +(y-2)^2=3^2
Po úprave: (x+1)^2 +(y-2)^2=9

Všeobecná rovnica kružnice

Podobne ako existuje niekoľko tvarov rovníc priamky, môžeme aj rovnicu kružnice zapísať rôznymi spôsobmi. Všeobecná rovnica kružnice je v tvare: x^2 +y^2-2mx-2ny+p=1.

Každá rovnica v tomto tvare ale nemusí ešte byť všeobecnou rovnicou kružnice. Pre všeobecnú rovnicu kružnice musí platiť, že výraz m^2+n^2-p je kladný. Praktické overenie, či ide o kružnicu, ale väčšinou vykonávame prevedením na stredovú rovnicu kružnice.

Príklad: Nájdite stred a polomer kružnice danej všeobecnou rovnicou x^2+y^2+4x+6y-12=0.

Najskôr si usporiadame členy podľa premenných: x^2+4x+y^2-6y-12=0.
Našim ďalším cieľom je upraviť výraz na ľavej strane ako súčet dvoch druhých mocnín (štvorcov), podľa vzorcov a^2\pm 2ab+b^2=(a\pm b)^2.
K obom stranám rovnice pripočítame konštanty 4 a 9, aby sme súčty členov s premennými x a y mohli upraviť na druhé mocniny (prevedieme v oboch prípadoch doplnenie na štvorec): x^2+4x+4+y^2-6y+9-12=4+9
A upravíme: (x+2)^2 +(y-3)^2-12=13
Na záver ešte prevedieme -12 na druhú stranu rovnice: (x+2)^2 +(y-3)^2=25
Týmto sme previedli všeobecnú rovnicu kružnice na stredovú rovnicu kružnice.
Polomer kružnice je r=\sqrt{25}=5.
Súradnice stredu S[m,n] odčítame v stredovej rovnici od premenných x a y, majú teda opačné znamienka než konštanty v zátvorkách v stredovej rovnici \Rightarrow S[-2;3].

Kružnica a priamka

priamka s pretína kružnicu v dvoch bodoch – sečnica kružnice
priamka t pretína kružnicu v jednom bode – dotyčnica kružnice
priamka v kružnici nepretína – vonkajšia priamka kružnice

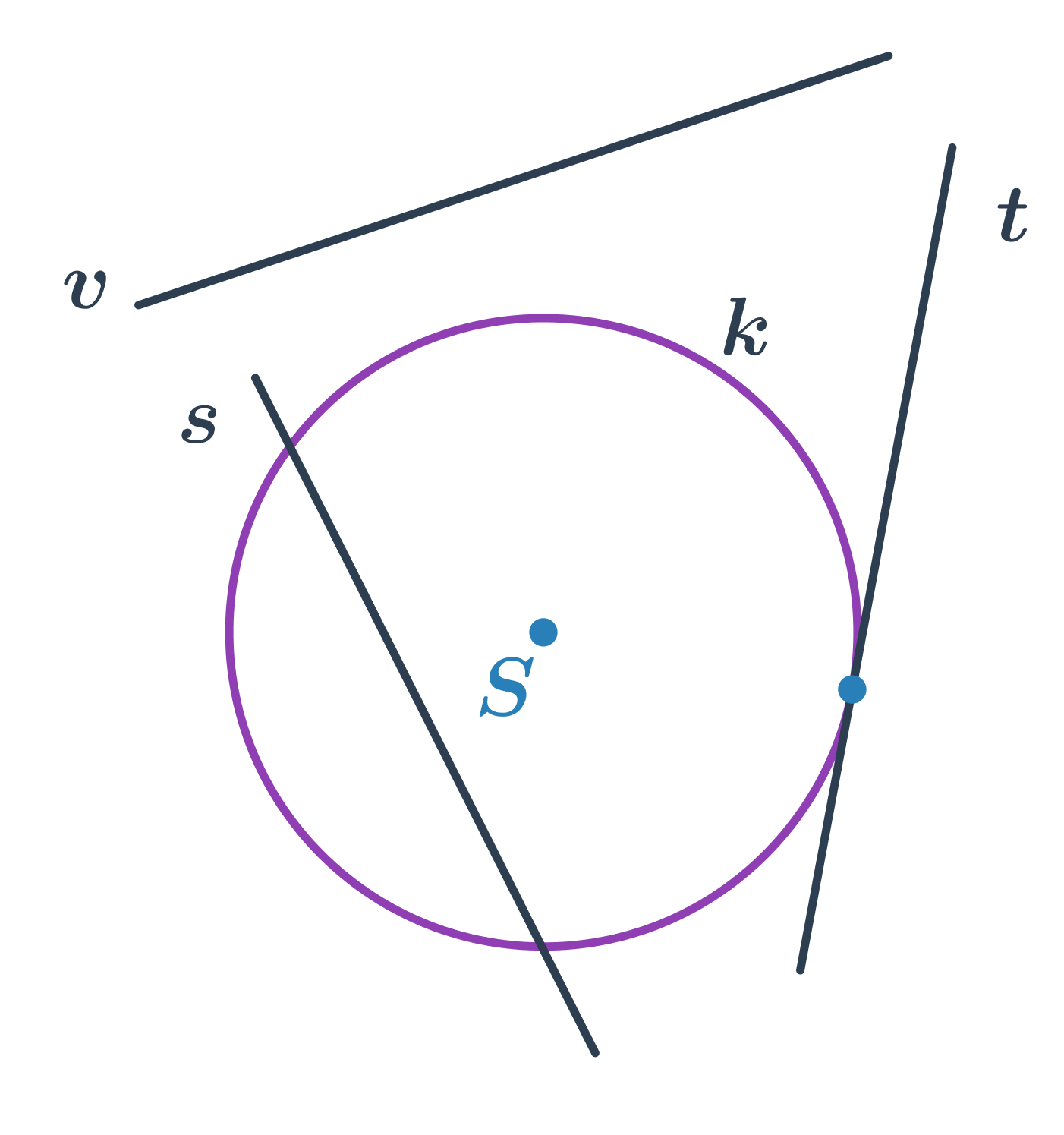
Rovnice dotyčnice kružnice v bode, ktorý leží na kružnici

Kružnica daná rovnicou (x-m)^2 +(y-n)^2=r^2 má v bode T[x_0;y_0] dotyčnicu (x_0-m)(x-m) +(y_0-n)(y-n)=r^2.

Ako si zapamätať rovnicu dotyčnice

Stredová rovnica je v tvare (x-m)^2 +(y-n)^2=r^2.
Zátvorky rozložíme na súčiny dvojčlenov (x-m)(x-m) +(y-n)(y-n)=r^2.
V každom súčine zameníme jedno x za x_0 a jedno y za y_0
Dostaneme rovnicu dotyčnice (x_0-m)(x-m) +(y_0-n)(y-n)=r^2

Príklad: Určite rovnicu dotyčnice kružnice (x-1)^2+(y+2)^2=13 v jej bode T[3;1].

Overíme, či bod T leží na kružnici: (3-1)^2+(1+2)^2=13 \Rightarrow 4+9=13
Dotyčnica má rovnicu (x_0-m)(x-m) +(y_0-n)(y-n)=r^2
Dosadíme súradnice bodu T: (3-1)(x-1) +(1+2)(y+2)=13
Roznásobíme zátvorky: 2x-2 +3y+6=13
A dostaneme všeobecnú rovnicu dotyčnice 2x+3y-9=0

Polára kružnice

Z bodu R mimo kružnicu môžeme zostrojiť dve dotyčnice k danej kružnici. Priamka určená bodmi dotyku dotyčníc sa nazýva polára kružnice vzhľadom k bodu R.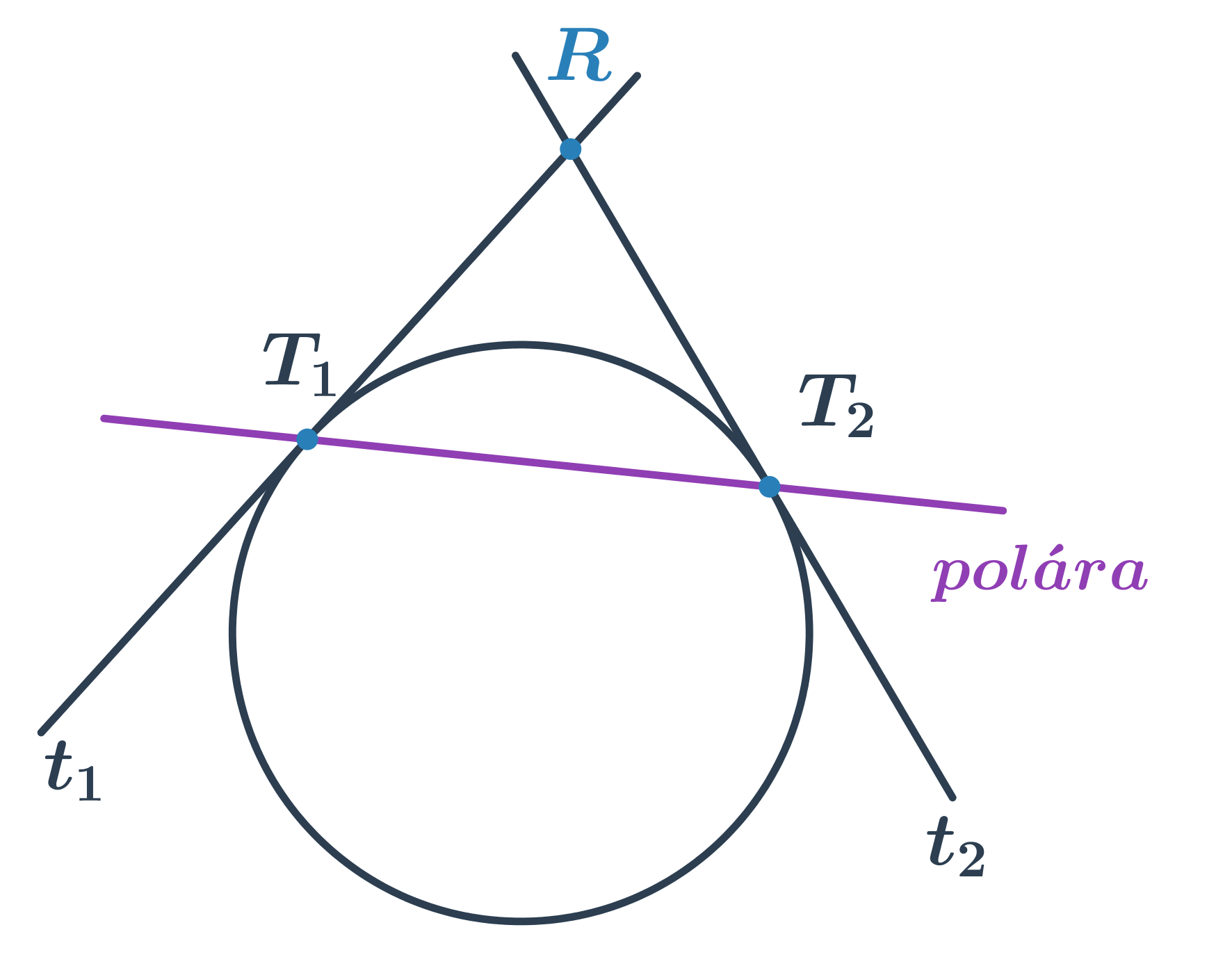

Rovnica poláry kružnice (x-m)^2 +(y-n)^2=r^2 vzhľadom k bodu R[r_1;r_2] je (r_1-m)(x-m) +(r_2-n)(y-n)=r^2.

Na čo poláru použijeme?

Poláru využívame na konštrukciu dotyčníc ležiacich z bodu mimo kružnicu.
Podľa vzorca určíme rovnicu poláry, teda priamky.
Nájdeme priesečníky poláry a kružnice – to sú body dotyku hľadaných dotyčníc.
Keď poznáme body dotyku, určíme podľa vzťahu pre rovnicu dotyčnice v bode kružnice všeobecné rovnice oboch dotyčníc.

Elipsa

Prejsť k cvičeniam s touto témou »

Elipsa je množina všetkých bodov v rovine, ktoré majú od dvoch rôznych bodov (ohnísk) stály súčet vzdialeností 2a, ktorý je väčší než vzdialenosť ohnísk.

Stredová rovnica elipsy

Tvar stredovej rovnice elipsy so stredom S[m;n] s veľkosťami hlavnej a vedľajšej polosi a a b závisí od polohy hlavnej osi:

hlavná os je rovnobežná s osou x, rovnica je v tvare: \frac{(x-m)^2}{a^2} +\frac{(y-n)^2}{b^2}=1
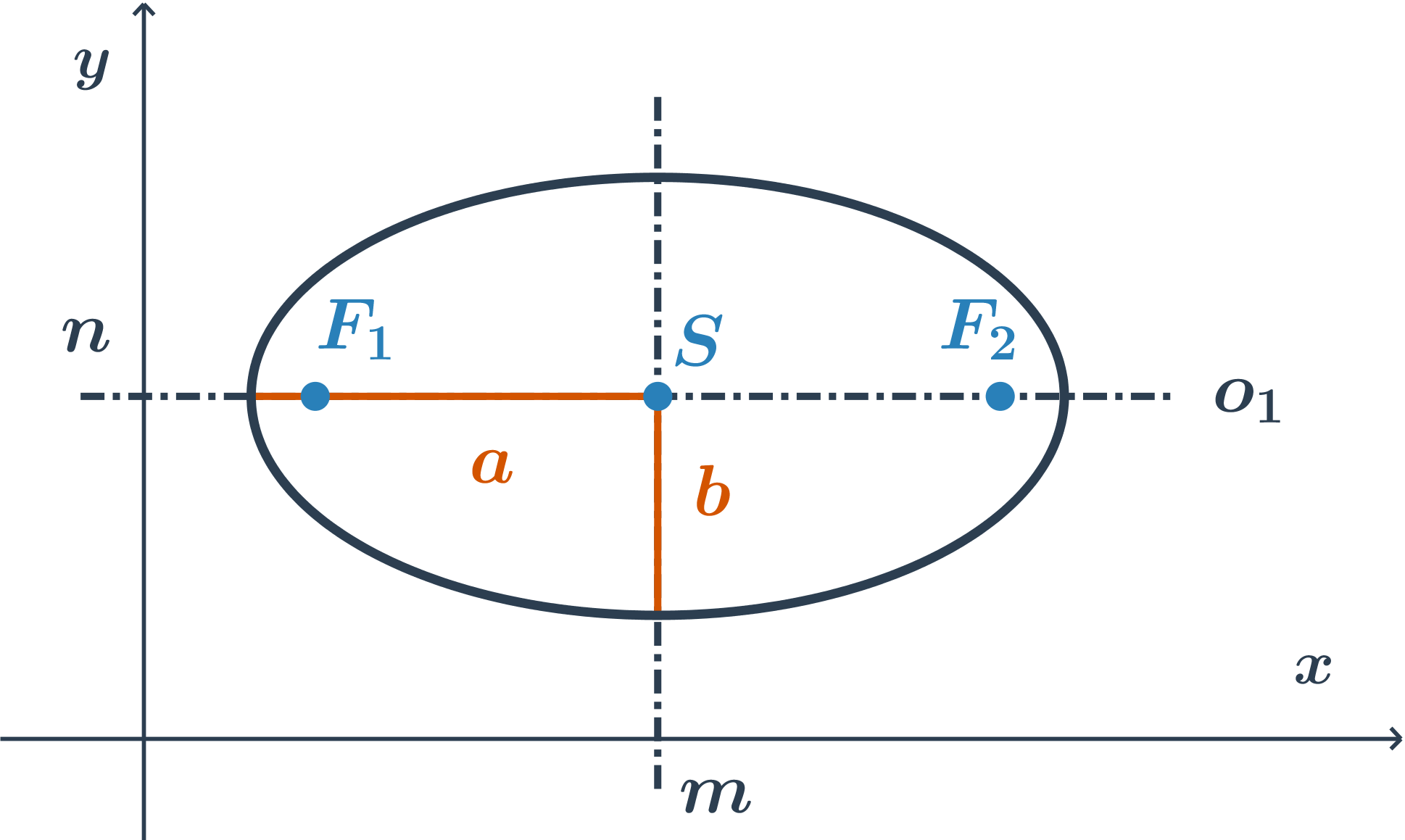
hlavná os je rovnobežná s osou y, rovnica je v tvare: \frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1

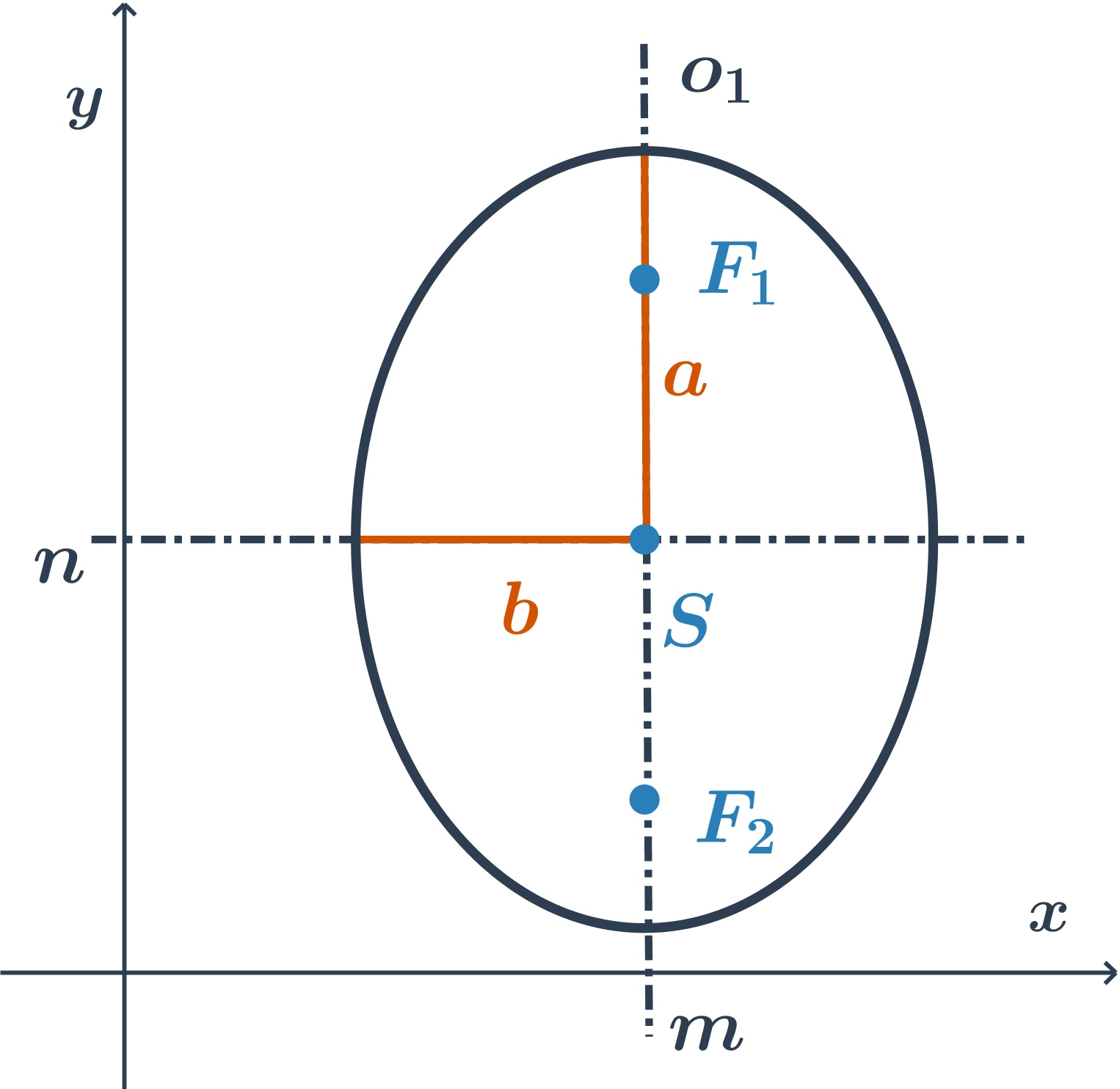
Návod: ako z rovnice zistiť, s ktorou súradnicovou osou je rovnobežná hlavná os elipsy

Pozrieme sa do menovateľov.
Väčší menovateľ je druhá mocnina veľkosti hlavnej polosi (a menší menovateľ je druhá mocnina veľkosti vedľajšej polosi).
Premenná v danom čitateli (zlomku s väčším menovateľom) potom určuje, s ktorou osou je hlavná os elipsy rovnobežná.
Stručne povedané: ak je väčšie číslo napríklad v menovateli s premennou x, je hlavná os rovnobežná s osou x.

Príklad: určenie stredovej rovnice elipsy s daným stredom, veľkosťami polosí a smerom hlavnej osi

Určite stredovú rovnicu elipsy so stredom v bode S[-2;3], je‑li a=3, b=2 ak hlavná os je rovnobežná s osou y.

Stredová rovnica je v tvare \frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1.
Dosadíme súradnice stredu a veľkosti hlavnej a vedľajšej polosi. Pri dosadení si dáme pozor na to, že súradnice stredu odčítame: \frac{(x-(-2))^2}{2^2} +\frac{(y-3)^2}{3^2}=1
Po úprave: \frac{(x+2)^2}{4} +\frac{(y-3)^2}{9}=1

Všeobecná rovnica elipsy

Podobne ako existuje niekoľko rovníc priamky, môžeme aj rovnicu elipsy zapísať iným spôsobom. Všeobecná rovnica elipsy je v tvare:

Ax^2 +By^2+Cx+Dy+E=1, A\ne B, A\cdot B>0.

Každá rovnica v tomto tvare ale nemusí byť všeobecnou rovnicou elipsy. Praktické overenie, či ide o elipsu vykonávame prevedením na stredovú rovnicu.

Príklad: určuje daná rovnica elipsu?

Rozhodnite, či rovnica x^2+3y^2+8x-18y+31=0 určuje elipsu.

Najskôr si usporiadame členy: x^2+8x+3y^2-18y+31=0.
Z členov s premennou y vytkneme 3: x^2+8x+3(y^2-6y)+31=0
K obom stranám rovnice pripočítame konštanty 16 a 27, aby sme členy s premennými x a y mohli upraviť podľa vzťahu (a\pm b)^2=a^2 \pm 2ab +b^2.
Máme: x^2+8x+16+3(y^2-6y+9)+31=16+27
A upravíme: (x+4)^2 +3(y-3)^2+31=43
Prevedieme konštantu 31 na druhú stranu rovnice: (x+4)^2 +3(y-3)^2=12
Na záver rovnicu vydelíme 12: \frac{(x+4)^2}{12} +\frac{(y-3)^2}{4}=1
Ide teda o elipsu.

Elipsa a priamka

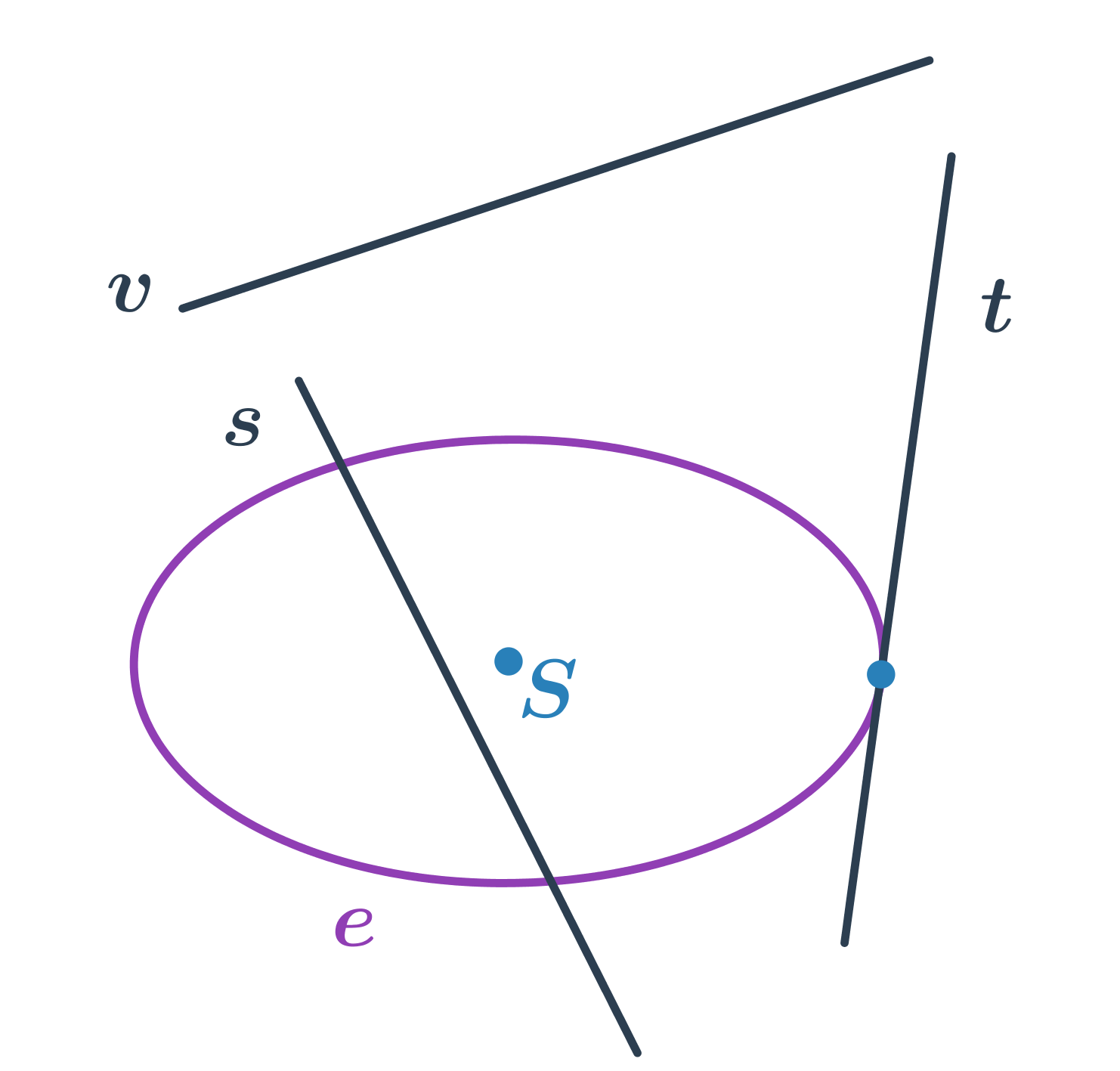
priamka s pretína elipsu v dvoch bodoch – sečnica elipsy
priamka t pretína elipsu v jednom bode – dotyčnica elipsy
priamka v elipsu nepretína – vonkajšia priamka elipsy

Rovnice dotyčnice elipsy v bode, ktorý leží na elipse

Elipsa daná rovnicou \frac{(x-m)^2}{a^2} +\frac{(y-n)^2}{b^2}=1 má v bode T[x_0;y_0] dotyčnicu určenú rovnicou:

\frac{(x-m)(x_0-m)}{a^2} +\frac{(y-n)(y_0-n)}{b^2}=1

Podobne môžeme zapísať aj rovnicu dotyčnice elipsy, ktorá má hlavnú os rovnobežnú s osou y.

Príklad: určenie rovnice dotyčnice elipsy v jej danom bode

Určite rovnicu dotyčnice elipsy \frac{(x-2)^2}{9} +\frac{(y-2)^2}{18}=1 v jej bode T[1;-2].

Overíme, či bod T leží na elipse: \frac{(1-2)^2}{9} +\frac{(-2-2)^2}{18}=1 \Rightarrow \frac19+\frac{16}{18}=1 \Rightarrow 1=1
Dotyčnica má rovnicu \frac{(x-m)(x_0-m)}{b^2} +\frac{(y-n)(y_0-n)}{a^2}=1
Dosadíme súradnice bodu T: \frac{(x-2)(1-2)}{9} +\frac{(y-2)(-2-2)}{18}=1
Zbavíme sa zlomkov: 2(x-2)\cdot(-1) +(y-2)\cdot(-4)=18
Roznásobíme zátvorky: -2x+4 -4y+8=18
A dostaneme všeobecnú rovnicu dotyčnice: x+2y+3=0

Parabola

Prejsť k cvičeniam s touto témou »

Parabola je množina všetkých bodov roviny, ktoré majú rovnakú vzdialenosť od daného bodu (ohnisko) a danej priamky (riadiaca priamka).

Vrcholová rovnica paraboly

Tvar rovnice závisí od umiestnenia osi:

os paraboly rovnobežná s osou y, vrcholová rovnice má potom tvar: (x-m)^2=\pm 2p(y-n)
os paraboly rovnobežná s osou x, vrcholová rovnica má potom tvar: (y-n)^2=\pm 2p(x-m)

V rovnici paraboly označujú m, n súradnice vrcholu paraboly, teda vrchol je bod V=[m;n]. Ďalej p je parameter paraboly = vzdialenosť ohniska od riadiacej priamky. Znamienko pred parametrom závisí od polohy na vrchole vzhľadom k bodom paraboly.

Príklad paraboly s osou rovnobežnou s osou y

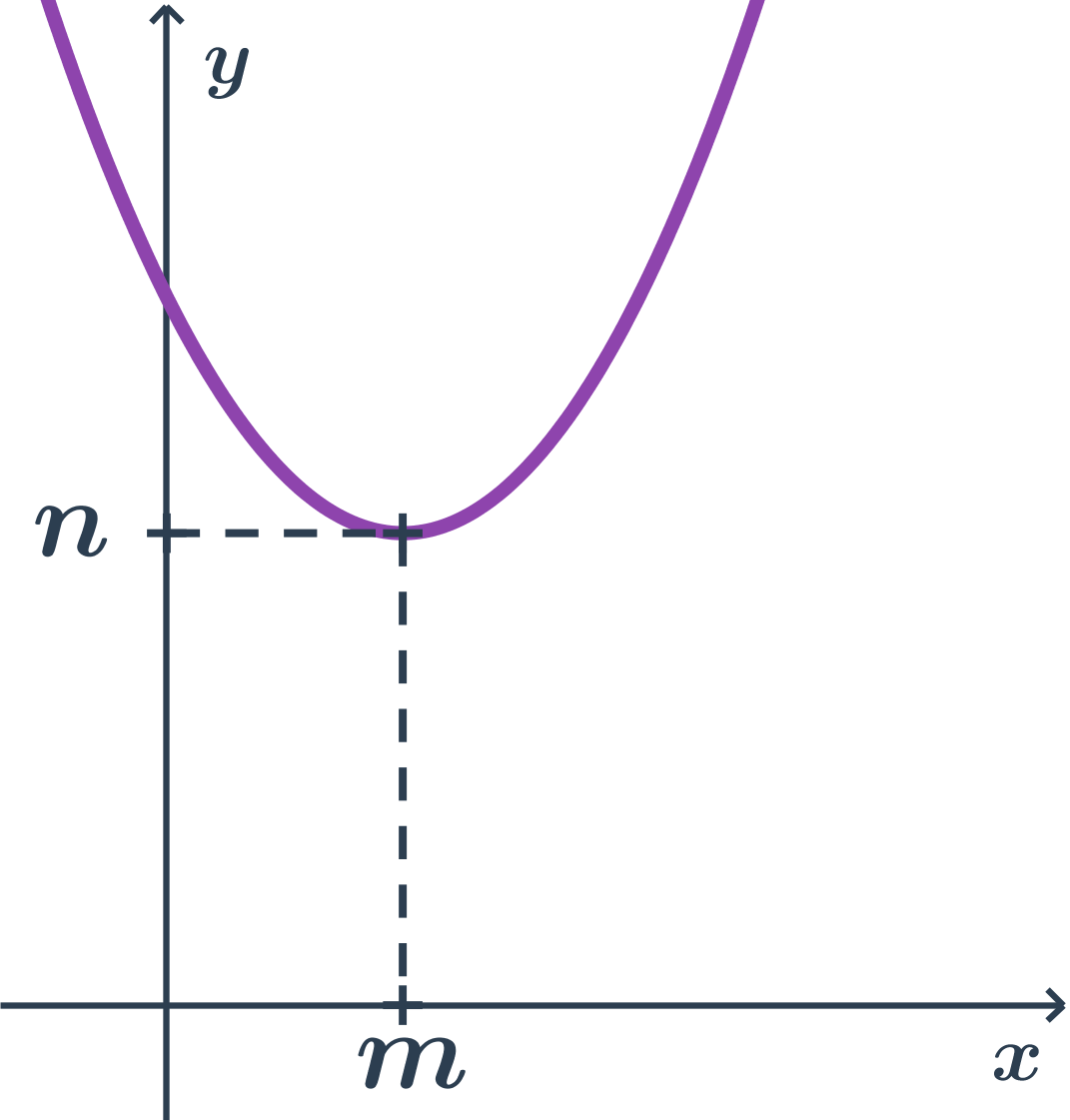
body paraboly majú y súradnicu aspoň tak veľkú ako vrchol (teda n)
vrcholová rovnica: (x-m)^2= + 2p(y-n)

Príklad paraboly s osou rovnobežnou s osou y, druhá orientácia

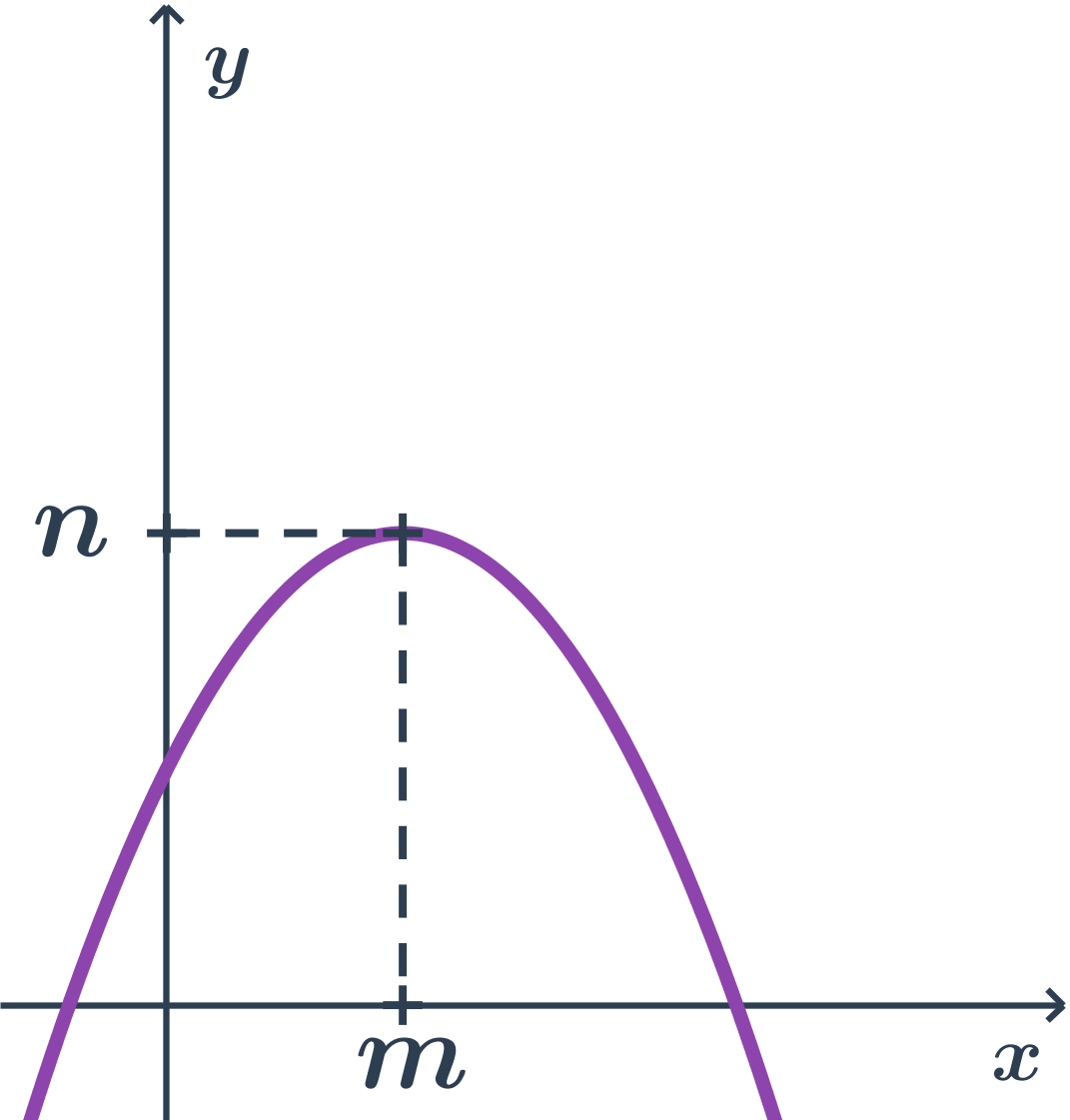
body paraboly majú y súradnicu najviac tak veľkú ako vrchol (teda n)
vrcholová rovnica: (x-m)^2= - 2p(y-n)

Príklad paraboly s osou rovnobežnou s osou x

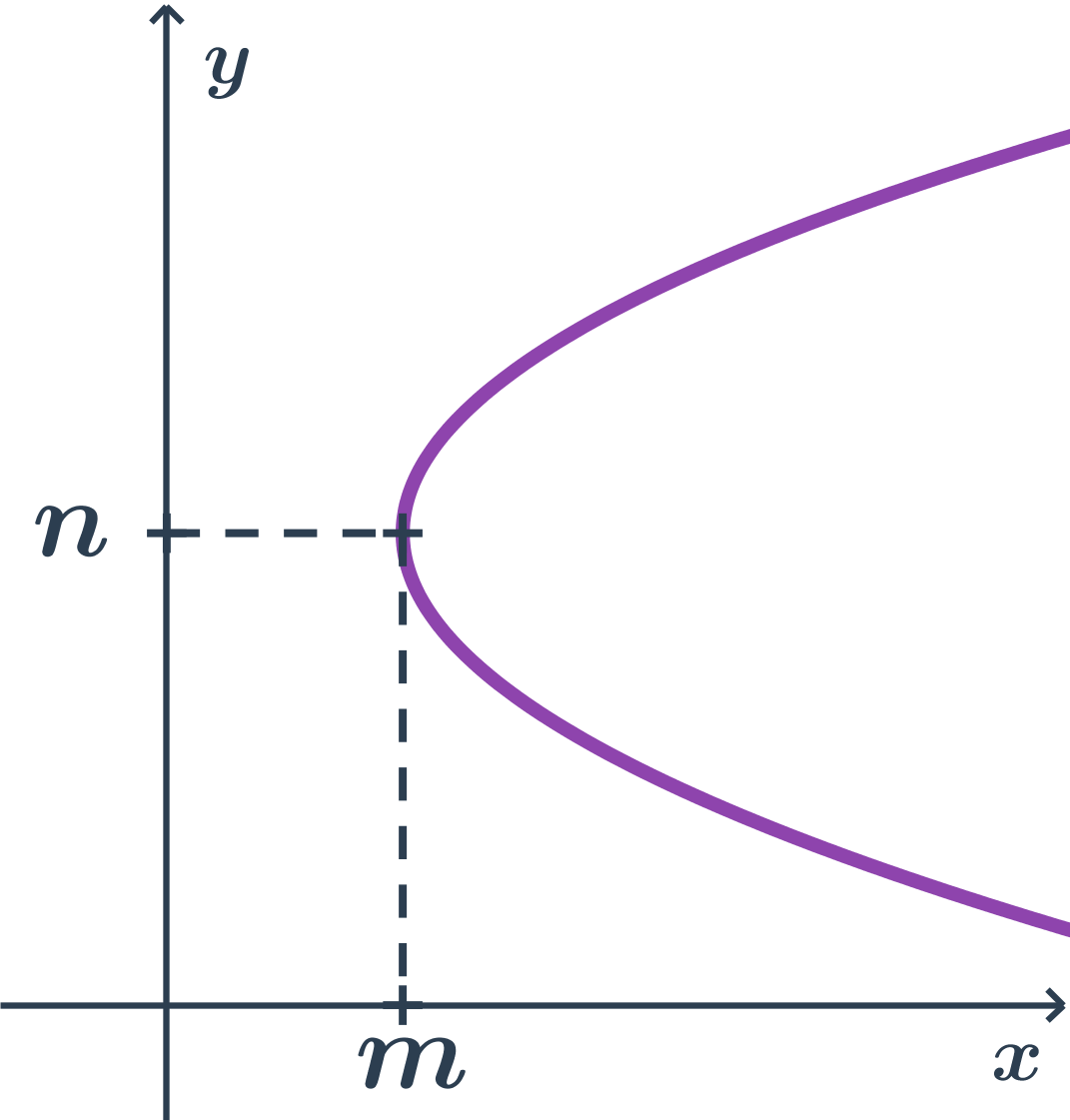
body paraboly majú x súradnicu aspoň tak veľkú ako vrchol (teda m)
vrcholová rovnica: (y-n)^2= + 2p(x-m)

Príklad paraboly s osou rovnobežnou s osou x, druhá orientácia

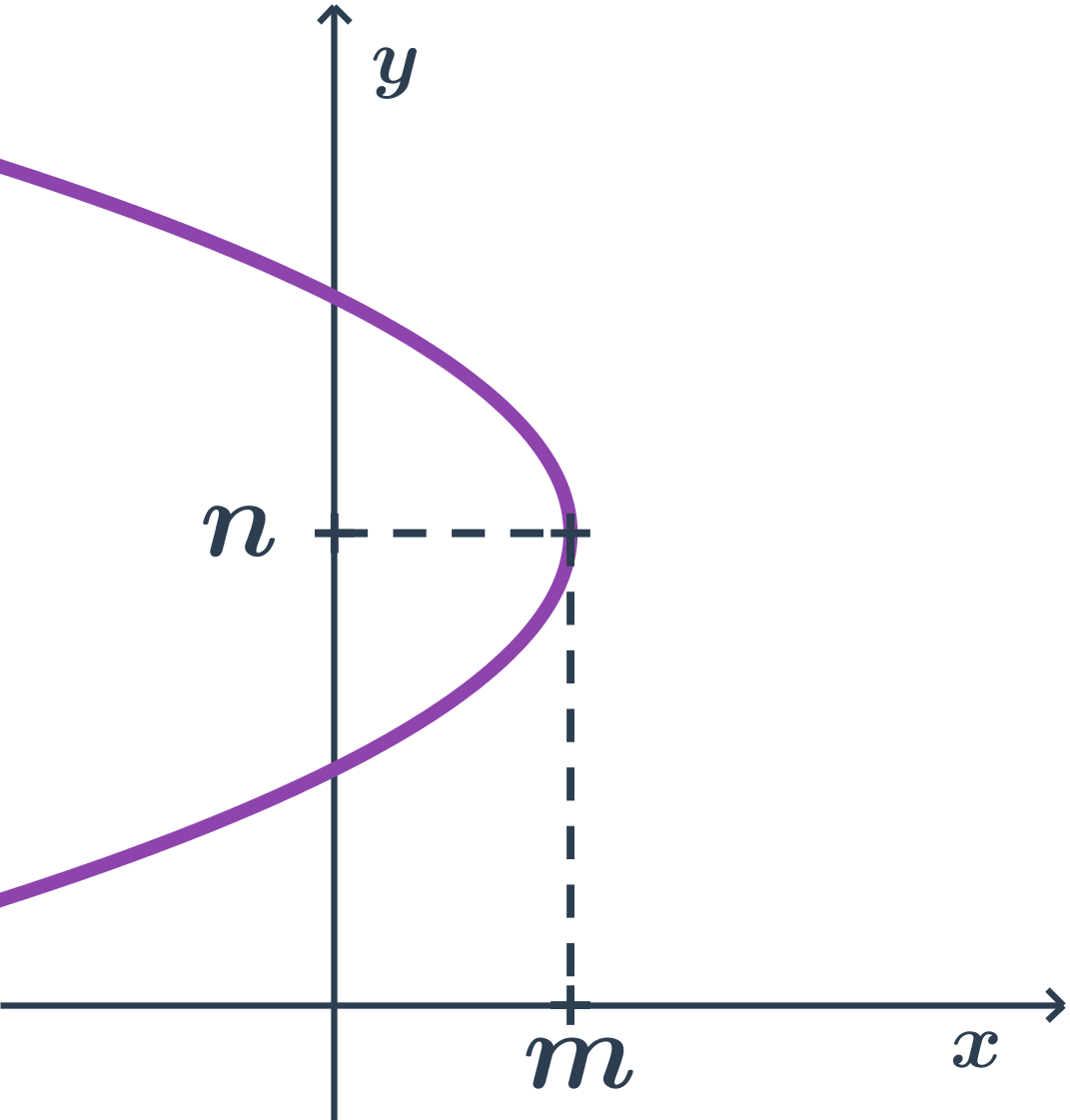
body paraboly majú x súradnicu najviac tak veľkú ako vrchol (teda m)
vrcholová rovnica: (y-n)^2= - 2p(x-m)

Všeobecná rovnica paraboly

Tvar rovnice závisí od umiestnenia osi:

os paraboly je rovnobežná s osou y: y=ax^2+bx+c
os paraboly je rovnobežná s osou x: x=ay^2+bx+c

Príklad paraboly s osou rovnobežnou s osou y, všeobecná rovnica

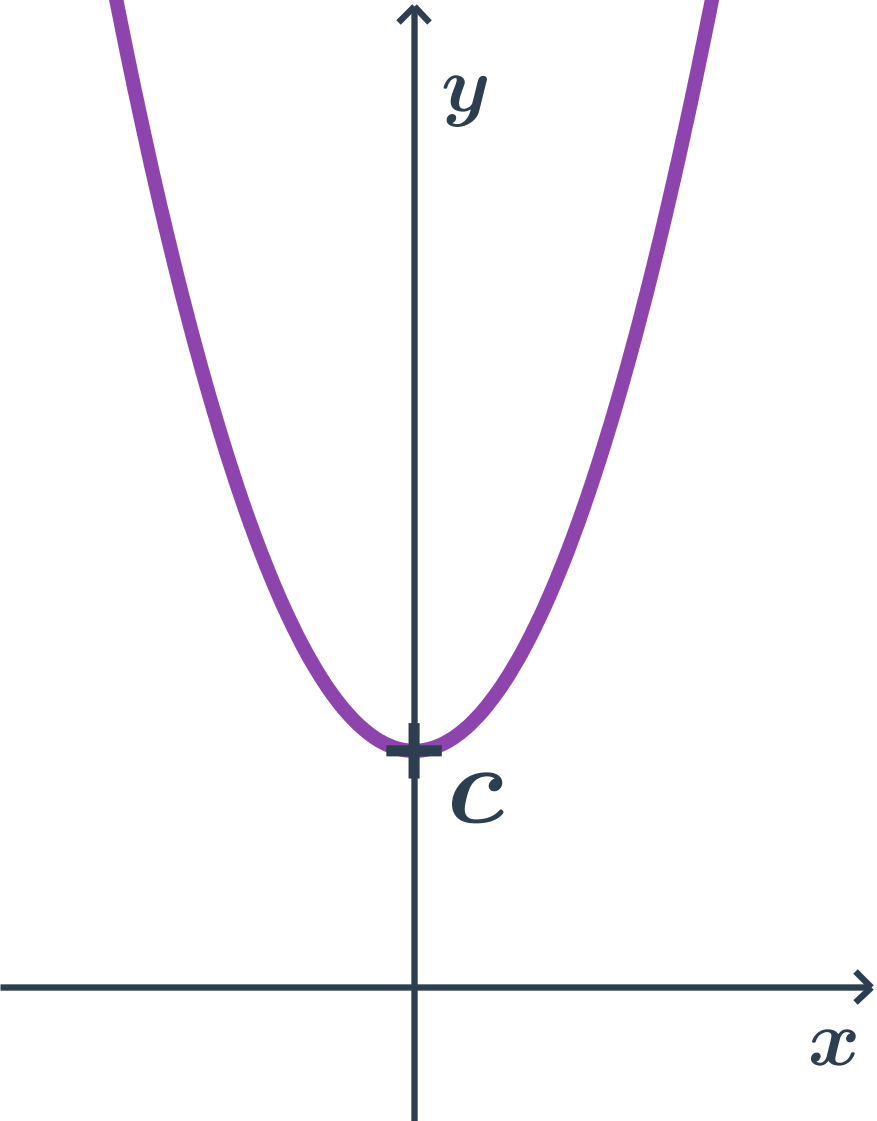
všeobecná rovnica: y=ax^2+bx+c
kde a>0

Príklad paraboly s osou rovnobežnou s osou y, druhá orientácia, všeobecná rovnica

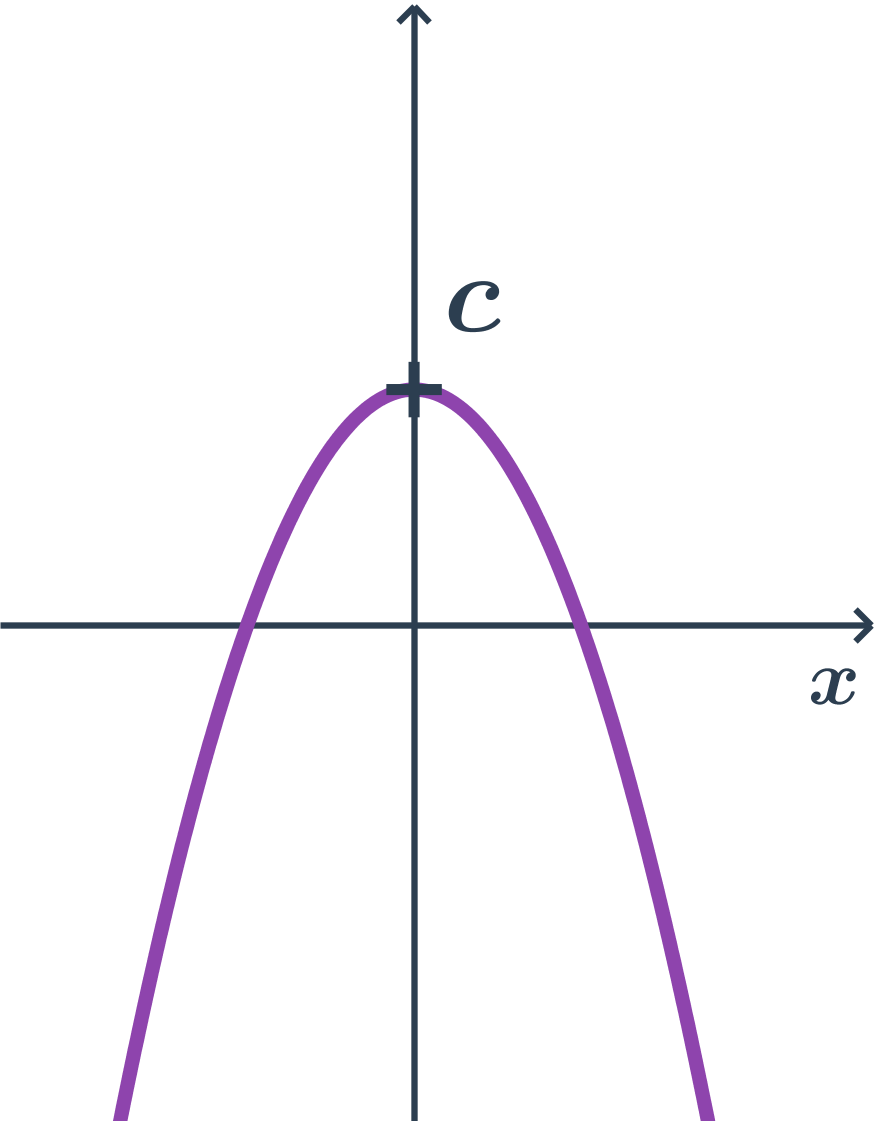
všeobecná rovnica: y=ax^2+bx+c
kde a<0

Príklad paraboly s osou rovnobežnou s osou x, všeobecná rovnica

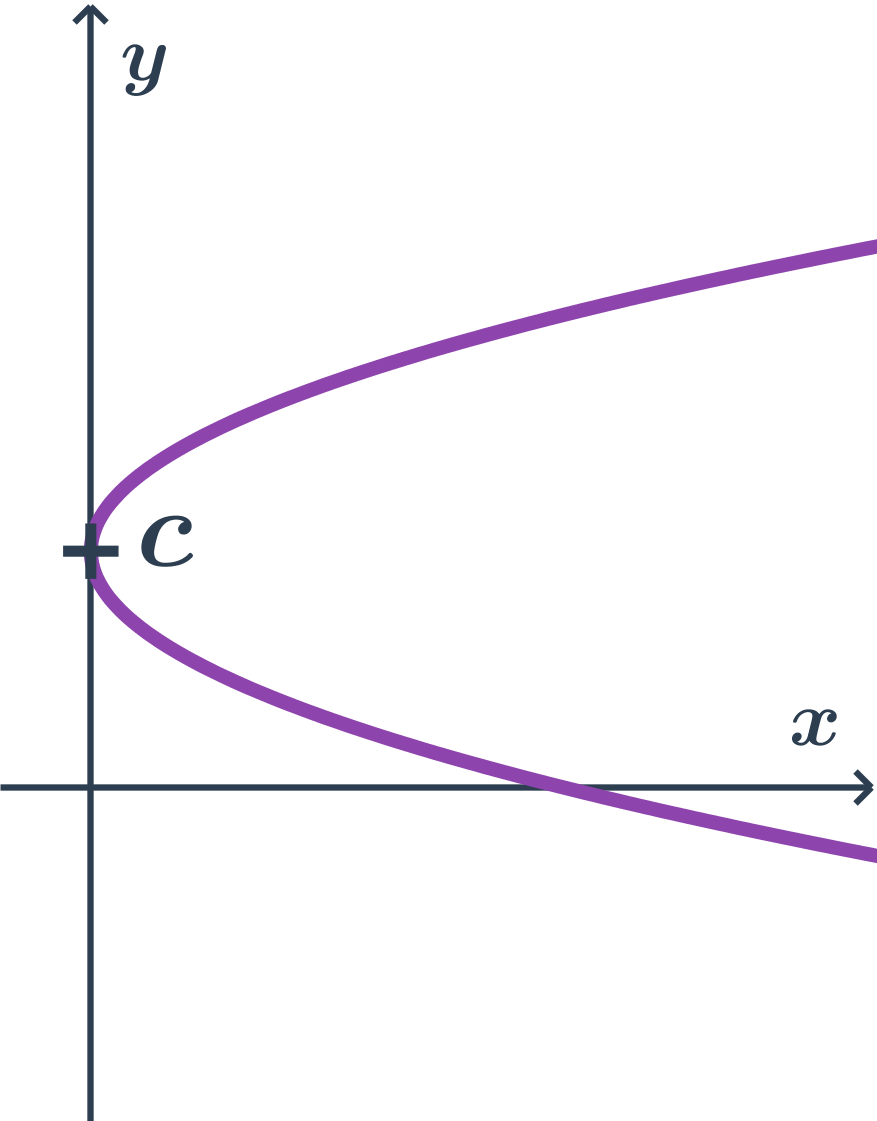
všeobecná rovnica: x=ay^2+bx+c
kde a>0

Príklad paraboly s osou rovnobežnou s osou x, druhá orientácia, všeobecná rovnica

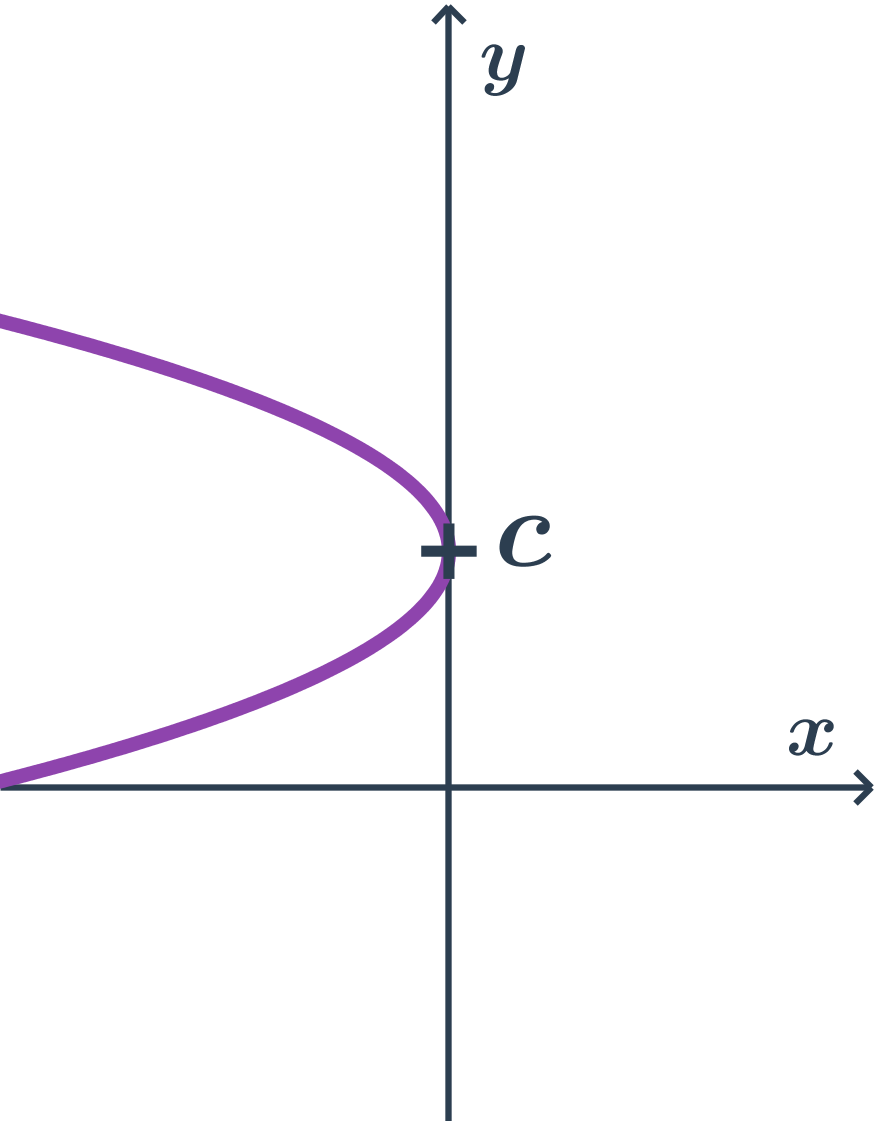
všeobecná rovnica: x=ay^2+bx+c
kde a<0

Priamka a parabola

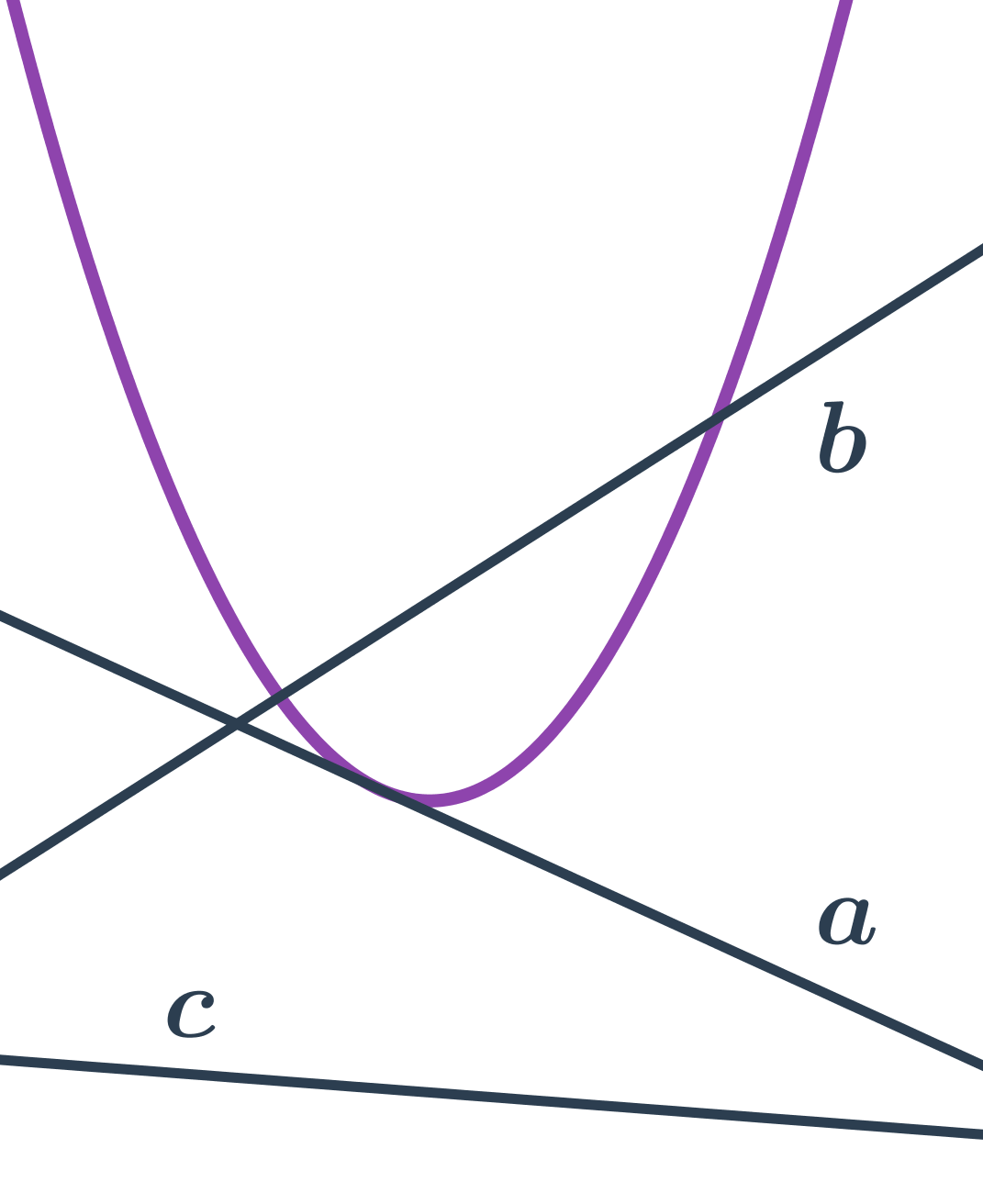
priamka b pretína parabolu v dvoch bodoch – sečnica paraboly
priamka a sa dotýka paraboly v jednom bode – dotyčnica paraboly
priamka c nepretína parabolu

Rovnica dotyčnice paraboly v bode, ktorý leží na parabole

parabola daná rovnicou (x-m)^2=\pm 2p(y-n) má v bode T=[x_0;y_0] dotyčnicu: (x-m)(x-x_0)=\pm p(y-n)\pm p(y-y_0)
parabola daná rovnicou (y-n)^2=\pm 2p(x-m) má v bode T=[x_0;y_0] dotyčnicu: (y-n)(y-y_0)=\pm p(x-m)\pm p(x-x_0)

Príklad dotyčnice paraboly v bode

majme parabolu danú vrcholovou rovnicou: (x-2)^2=2(y-1)
pre túto parabolu je m=2, n=1, p=1
na tejto parabole leží (súradnica spĺňajúca rovnicu) napríklad bod T=[4;3]
dotyčnica danej paraboly v bode T=[4;3] má rovnicu: (x-2)(x-4)= (y-1)+(y-3)

Druhý príklad dotyčnice paraboly v bode

majme parabolu danú vrcholovou rovnicou: (x-2)^2=-4(y-1)
pre túto parabolu je m=2, n=1, p=2
na tejto parabole leží (súradnice spĺňajú rovnicu) napríklad bod T=[6;-3]
dotyčnica danej paraboly v bode T=[6;-3] má rovnicu: (x-2)(x-6)= -2(y-1)-2(y+3)

Hyperbola

Prejsť k cvičeniam s touto témou »

Hyperbola je množina všetkých bodov v rovine, ktoré majú od dvoch rôznych bodov (ohnísk) stály rozdiel vzdialeností 2a, ktorý je menší než vzdialenosť ohnísk. Hyperbola sa skladá z dvoch častí – vetiev hyperboly. Tieto dve vetvy sa blížia k priamkam, ktoré nazývame asymptoty.

Stredová rovnica hyperboly

Tvar stredovej rovnice hyperboly so stredom S[m;n] s veľkosťami hlavnej a vedľajšej polosi a,b závisí od polohy hlavnej osi.

Stredová rovnica hyperboly s hlavnou osou rovnobežnou s osou x

Ak je hlavná os rovnobežná s osou x, rovnica je v tvare \frac{(x-m)^2}{a^2} -\frac{(y-n)^2}{b^2}=1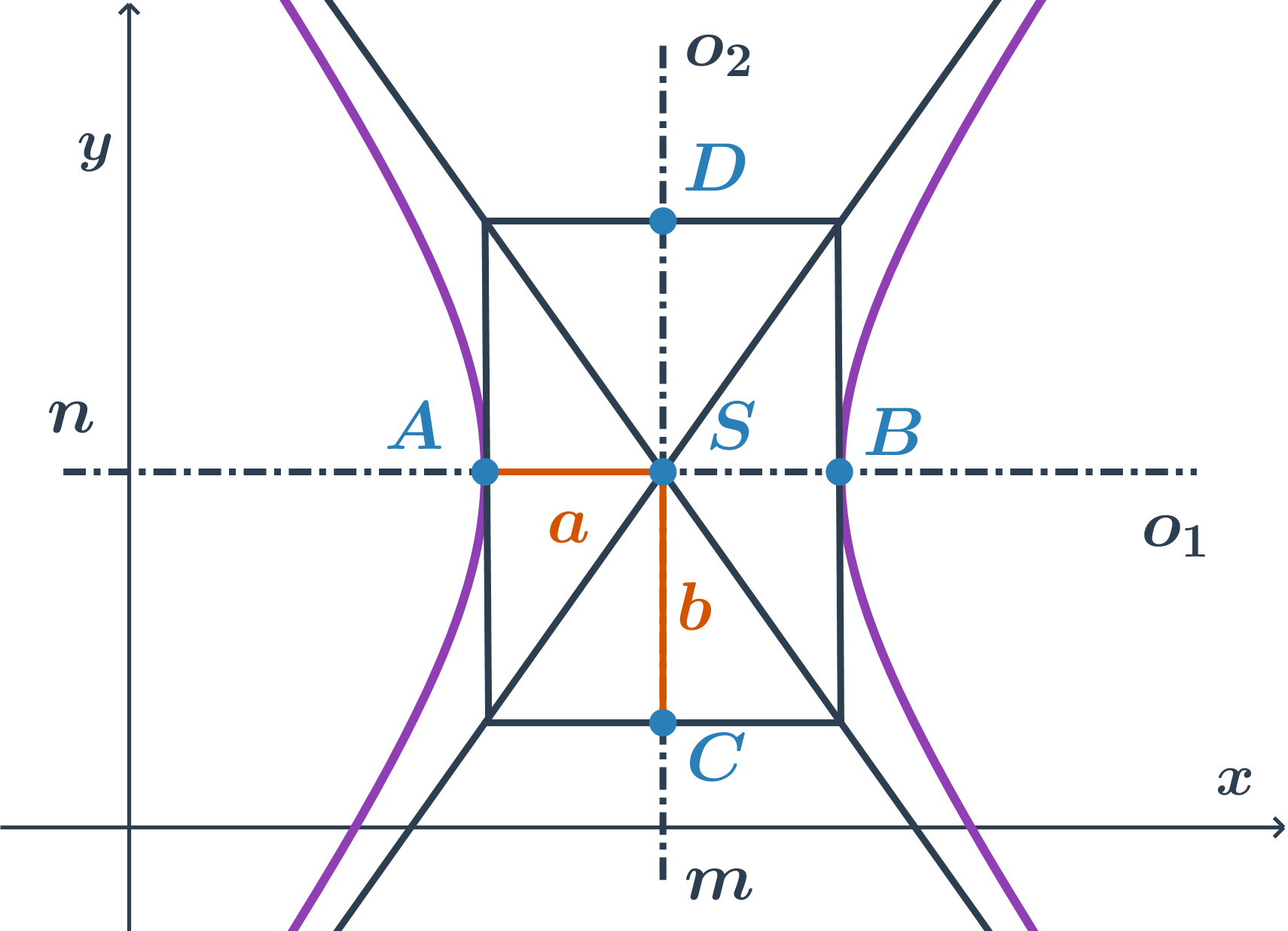

Stredová rovnica hyperboly s hlavnou osou rovnobežnou s osou y

Ak je hlavná os rovnobežná s osou y, rovnica je v tvare -\frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1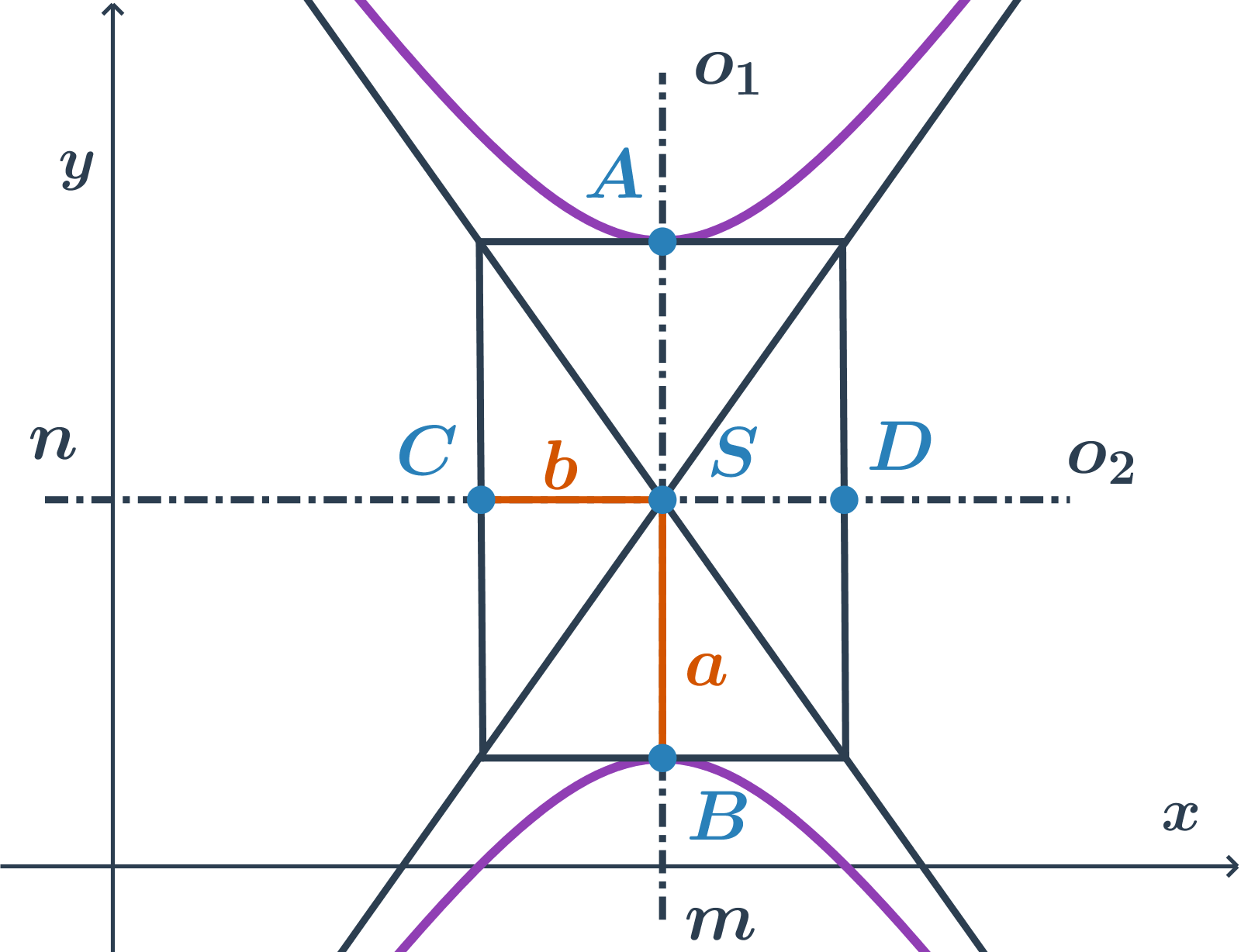

Oproti elipse, nemusí byť v prípade hyperboly vždy hlavná polos a dlhšia než vedľajšia polos b. Pre rovnoosú hyperbolu dokonca platí a=b.

Ako zo stredovej rovnice poznáme, s ktorou súradnicovou osou je rovnobežná hlavná os hyperboly?

Pozrieme sa na znamienka členov s premennou x a y.
Premenná v člene, ktorý má pred sebou znamienko plus udáva, s ktorou súradnicovou osou je rovnobežná hlavná os hyperboly.
V menovateli danej premennej je potom (v druhej mocnine) veľkosť hlavnej polosi.
Stručne povedané: ak je znamienko plus napríklad v prípade člena s premennou x, je hlavná os rovnobežná s osou x a v menovateli je druhá mocnina veľkosti hlavnej polosi a.

Príklad: Určenie stredovej rovnice hyperboly

Určite stredovú rovnicu hyperboly so stredom v bode S[1;-5], ak je veľkosť hlavnej polosi 2, veľkosť vedľajšej polosi 6 a hlavná os je rovnobežná s osou y.

Stredová rovnica je v tvare -\frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1. Hlavná polos má veľkosť a, vedľajšia b.
Dosadíme súradnice stredu a veľkosti hlavnej a vedľajšej polosi. Pri dosadení si dáme pozor na to, že súradnice stredu odčítame: -\frac{(x-1)^2}{6^2} +\frac{(y-(-5))^2}{2^2}=1
Po úprave: -\frac{(x-1)^2}{36} +\frac{(y+5)^2}{4}=1

Rovnice asymptot

Už vieme, že asymptoty sú priamky, ku ktorým sa hyperbola blíži. Pomôžu pri vykreslení hyperboly. Rovnica asymptot závisí od tvaru stredovej rovnice hyperboly.

Pre hyperbolu danú rovnicou v tvare \frac{(x-m)^2}{a^2} -\frac{(y-n)^2}{b^2}=1 sú rovnice asymptot:

y=\pm\frac{b}{a}(x-m)+n

Pre hyperbolu danú rovnicou v tvare -\frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1 sú rovnice asymptot:

y=\pm\frac{a}{b}(x-m)+n

Ako načrtnúť hyperbolu?

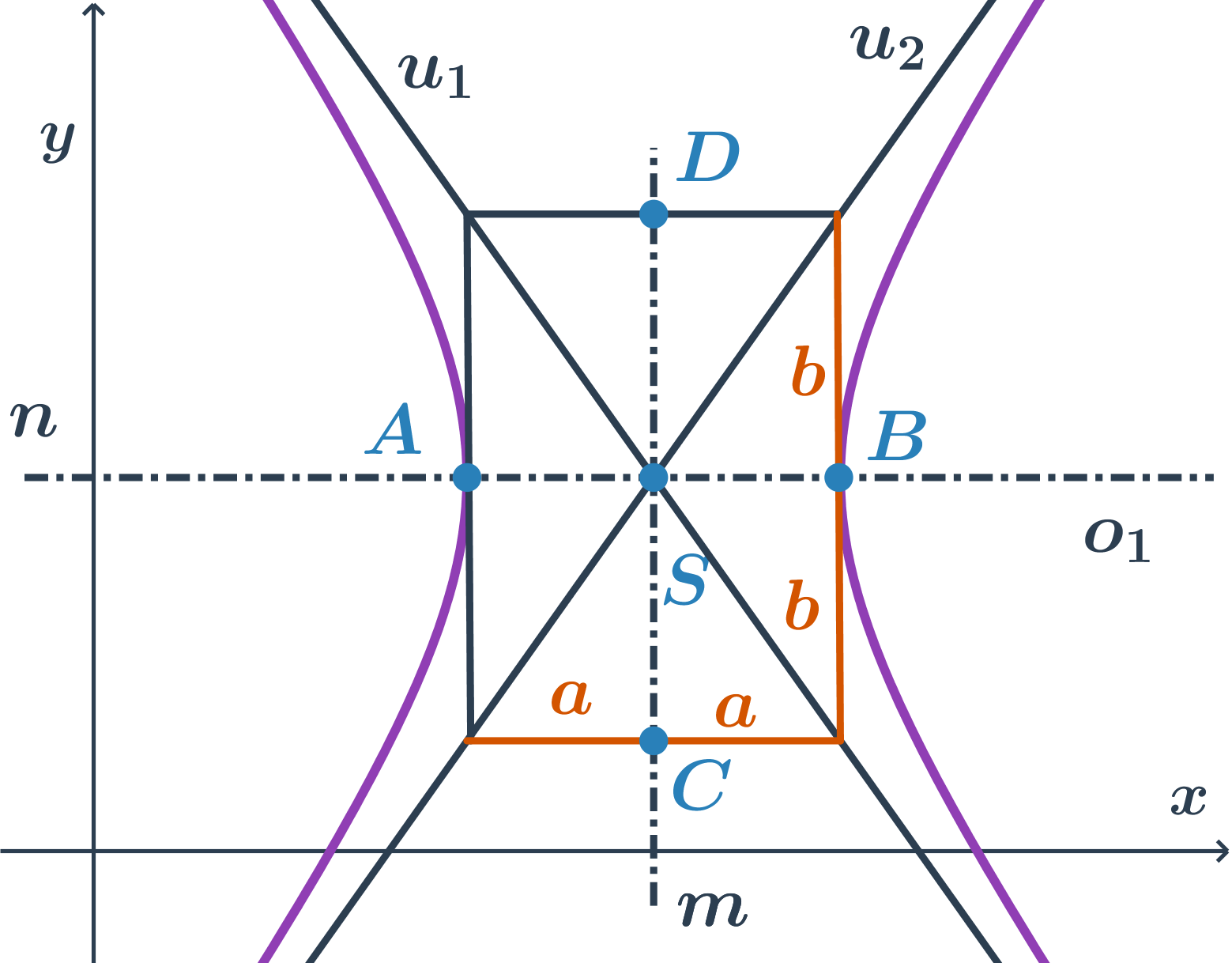
Najskôr si vyznačíme stred, hlavné a vedľajšie vrcholy.
Potom zostrojíme charakteristický obdĺžnik hyperboly. To je obdĺžnik, ktorý má strany rovnobežné s osami a vrcholmi hyperboly sú stredy jeho strán. Dĺžky jeho strán sú teda 2a a 2b.
Asymptoty sú uhlopriečky charakteristického obdĺžnika.

Všeobecná rovnica hyperboly

Podobne ako existuje niekoľko rovníc elipsy, môžeme aj rovnicu hyperboly zapísať rôznymi spôsobmi. Všeobecná rovnica hyperboly je v tvare: Ax^2 +By^2+Cx+Dy+E=1, A\cdot B<0. Podmienka A\cdot B<0 zaručuje, že konštanty A, B majú opačné znamienka. Každá rovnica v tomto tvare ale nemusí byť všeobecnou rovnicou hyperboly. Praktické overenie, či ide o hyperbolu vykonávame prevedením na stredovú rovnicu.

Príklad: Určuje daná rovnica hyperbolu?

Rozhodnite, či rovnica -x^2+2y^2+8x-18y+31=0 určuje hyperbolu.

Najskôr si usporiadame členy: -x^2+8x+y^2-18y+40=0.
Z členov s premennou x vytkneme -1: -(x^2-8x)+y^2-18y+40=0
K obom stranám rovnice pripočítame konštantu 81 a odčítame konštantu 16, aby sme členy s premennými x a y mohli upraviť podľa vzťahu pre (a\pm b)^2: -(x^2-8x+16)+y^2-18y+81+40=81-16
A upravíme: -(x-4)^2 +(y-9)^2+40=65
Prevedieme konštantu 40 na druhú stranu rovnice: -(x-4)^2 +(y-9)^2 =25
Na záver rovnice vydelíme 25: -\frac{(x-4)^2}{25} +\frac{(y-9)^2}{25}=1
Ide teda o hyperbolu. Hlavná os je rovnobežná s osou y a a=b=5.

Hyperbola a priamka

priamka s pretína hyperbolu v dvoch bodoch – sečnica hyperboly
priamka t pretína hyperbolu v jednom bode – dotyčnica hyperboly
priamka v hyperbolu nepretína – vonkajšia priamka hyperboly

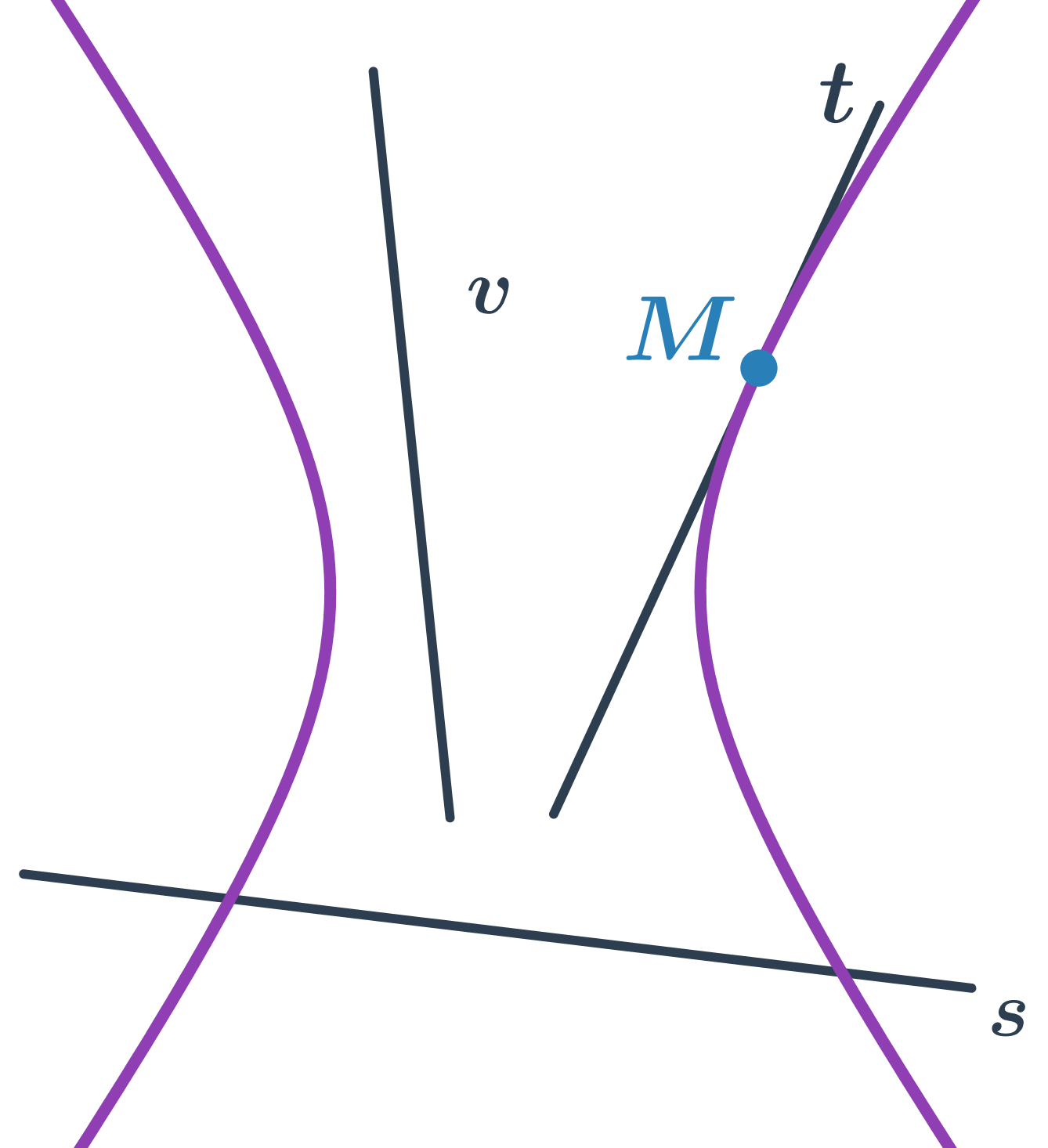
Špeciálnou polohou sečnice hyperboly je priamka, ktorá je rovnobežná s asymptotou. Taká sečnica potom pretína hyperbolu v jednom bode.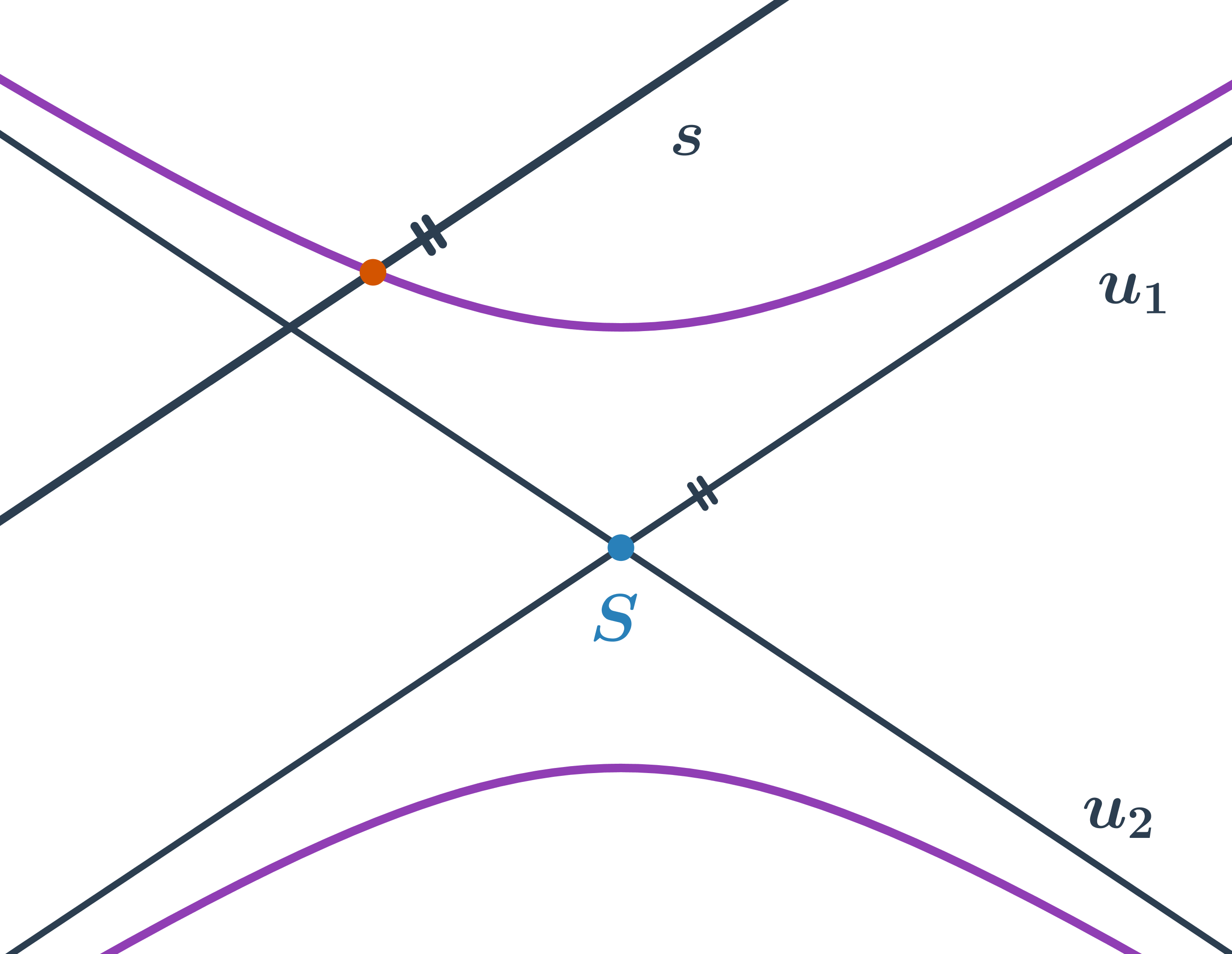

Ako rozlíšiť, či je priamka dotyčnica alebo sečnica?

Najskôr určíme vzájomnú polohu priamky a hyperboly.
Ak vyjdú dva priesečníky, ide o sečnicu vo všeobecnej polohe.
Ak vyjde jeden priesečník, musíme ešte rozhodnúť, či je priamka rovnobežná s asymptotou. Ak nie, ide o dotyčnicu. V opačnom prípade ide o sečnicu.

Rovnica dotyčnice hyperboly v bode, ktorý leží na hyperbole

Hyperbola daná rovnicou \frac{(x-m)^2}{a^2} -\frac{(y-n)^2}{b^2}=1 má v bode T[x_0;y_0] dotyčnicu danú rovnicou:

\frac{(x-m)(x_0-m)}{a^2} -\frac{(y-n)(y_0-n)}{b^2}=1.

Podobne môžeme zapísať aj rovnicu dotyčnice hyperboly, ktorá má hlavnú os rovnobežnú s osou y.

Výpis prehľadov

Kužeľosečky

Podkapitoly

Kužeľosečky

Kružnica (kužeľosečka)

Stredová rovnica kružnice

Všeobecná rovnica kružnice

Kružnica a priamka

Rovnice dotyčnice kružnice v bode, ktorý leží na kružnici

Polára kružnice

Elipsa

Stredová rovnica elipsy

Všeobecná rovnica elipsy

Elipsa a priamka

Rovnice dotyčnice elipsy v bode, ktorý leží na elipse

Parabola

Vrcholová rovnica paraboly

Všeobecná rovnica paraboly

Priamka a parabola

Rovnica dotyčnice paraboly v bode, ktorý leží na parabole

Hyperbola

Stredová rovnica hyperboly

Rovnice asymptot

Všeobecná rovnica hyperboly

Hyperbola a priamka

Rovnica dotyčnice hyperboly v bode, ktorý leží na hyperbole

Ďakujeme za vašu správu, bola úspešne odoslaná.

Napíšte nám

Neviete si rady?

Čoho sa správa týka?