Výpis prehľadov
Množiny
Prechádzate súhrny informácií k určitým témam. Systémy Vieme sa zameriavajú hlavne na ich precvičovanie. K cvičeniam k jednotlivým podtémam sa dostanete pomocou odkazov nižšie.
Podkapitoly
Množina je súbor prvkov. Množiny využívame ako čiastkový prvok v mnohých oblastiach matematiky. Príklad z geometrie: kružnica je množina bodov, ktoré majú rovnakú vzdialenosť od stredu. Množiny majú aj mnoho praktických využití. Napríklad pri vývoji internetového obchodu program pracuje s množinou dostupných výrobkov. Množiny sú tiež dôležité na štúdium základov matematiky. Pomáhajú nám napríklad ujasniť si, čo je to nekonečno.
Na prácu s množinami potrebujeme najskôr ovládnuť základné pojmy a značenie a pozrieť sa na rôzne spôsoby, ako môžeme množiny zapísať (vymenovaním, charakteristickou vlastnosťou, štandardným značením).
S množinami môžeme vykonávať množinové operácie ako sú zjednotenie a prienik. Tieto operácie je vhodné si najskôr precvičiť na konkrétnych príkladoch. Keď máme jasno v jednotlivých prípadoch, prichádzajú na rad všeobecné vlastnosti množín a množinových operácií. Na získanie pochopenia a intuície je vhodné zakreslovať si množiny pomocou Vennových diagramov.
Medzi pokročilejšie témy patria množiny množín a potenčná množina.
HoreMnožiny: pojmy a značenie
Množina je súbor prvkov. Pri množine nie je dôležité poradie prvkov a nezohľadňuje opakované výskyty prvkov. Nasledujúce množiny sú všetky rovnaké:
- \{\square, \bigcirc, \triangle\}
- \{\bigcirc, \triangle, \square\}
- \{\square, \square, \square, \bigcirc, \bigcirc, \triangle\}
| Značenie | Pojem | Komentár |
|---|---|---|
| \emptyset | prázdna množina | |
| \overline{A} | doplnok | prvky, ktoré nepatria do množiny A |
| x \in A | patria do množiny | prvky x patria do množiny A |
| A \cap B | prienik | prvky, ktoré patria do oboch množín A, B |
| A \cup B | zjednotenie | prvky, ktoré patria aspoň do jednej z množín A, B |
| A \setminus B | rozdiel | prvky, ktoré patria do množiny A, ale nepatria do B |
| A = B | rovnosť | rovnosť množín A, B |
| A \subseteq B | podmnožina | všetky prvky množiny A patria aj do množiny B |
| A \subset B | vlastná podmnožina | A je podmnožina B a súčasne A \neq B |
| (zvislá čiara)A(zvislá čiara) | veľkosť množiny | počet prvkov množiny |
| A \cap B = \emptyset | disjunktné množiny | množiny A, B nemajú žiadny spoločný prvok |
Zápis množín
Dôležité číselné množiny majú v matematike svoje štandardné označenie:
| \mathbb{N} | množina prirodzených čísel |
| \mathbb{Z} | množina celých čísel |
| \mathbb{Q} | množina racionálnych čísel |
| \mathbb{R} | množina reálnych čísel |
Ostatné množiny zapisujeme dvomi hlavnými spôsobmi:
Zápis vymenovaním. Jednoducho vymenujeme prvky množiny a zapíšeme ich pomocou zloženej zátvorky. Napríklad M = \{3, 7, 9\} je trojprvková množina obsahujúca čísla 3, 7 a 9.
Symbolický zápis množín. Určíme, zo ktorej množiny prvky vyberáme a akú musia spĺňať vlastnosť. Napríklad M = \{x \in \mathbb{N} \mid x \lt 10\} je množina prirodzených čísel menších než 10.
HoreMnožinové operácie
| Značenie | Pojem | Komentár |
|---|---|---|
| A \cap B | prienik | prvky, ktoré patria do oboch množín A, B |
| A \cup B | zjednotenie | prvky, ktoré patria aspoň do jednej z množín A, B |
| A \setminus B | rozdiel | prvky, ktoré patria do množiny A, ale nepatria do B |
| A \ominus B | symetrický rozdiel | prvky, ktoré patria práve do jednej z množín A a B |
Znázornenie množinových operácií pomocou Vennových diagramov:
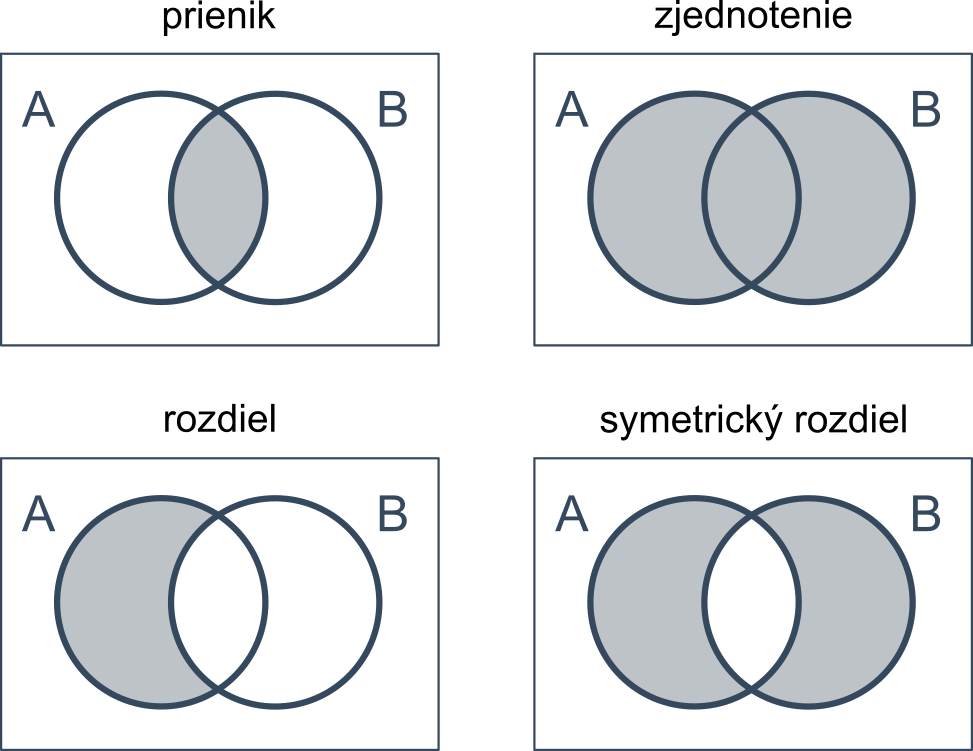
Vlastnosti množín a množinových operácií
- Každá množina je svojou podmnožinou: A\subseteq A.
- Množina nemôže byť svojou vlastnou podmnožinou.
- Prázdna množina je podmnožina akejkoľvek množiny: \emptyset \subseteq A.
- Prázdná množina nemá žiadnu vlastnú podmnožinu.
- A \subseteq A \cup B
- A \cap B \subseteq A
- A \subseteq A \wedge B \subseteq A \Leftrightarrow A=B
Vennove diagramy
Vennov diagram znázorňuje všetky možné vzťahy niekoľkých množín. Vennov diagram znázorňuje prvky množín ako body v rovine a množiny ako plochy vnútri kriviek. Najčastejšie používané sú Vennove diagramy pre dve a tri množiny, v ktorých sú množiny znázornené pomocou kruhov. Je možné stvárniť Vennove diagramy aj v prípade viacerých množín, ale k tomu si už nevystačíme s kruhmi (tieto diagramy nie sú prehľadné, a tak sa príliš nevyužívajú).
Typický Vennov diagram pre tri množiny:
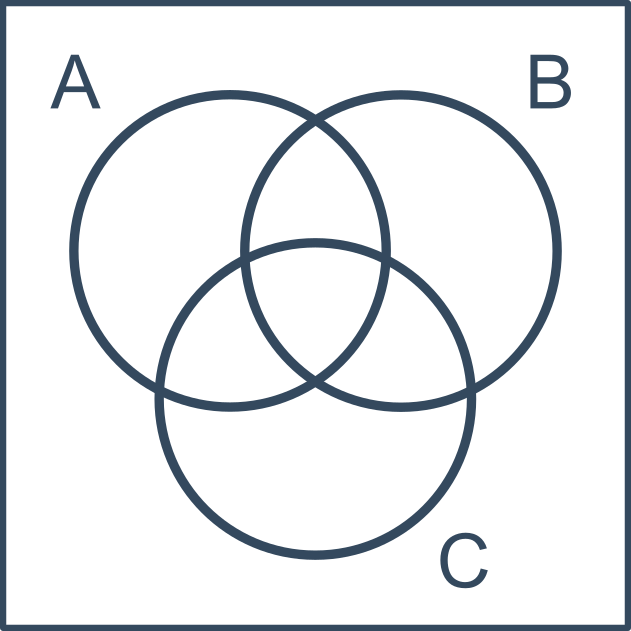
Príklad s konkrétnymi prvkami (množina A obsahuje červené útvary, množina B obsahuje kolieska, množina C obsahuje vyplnené útvary):
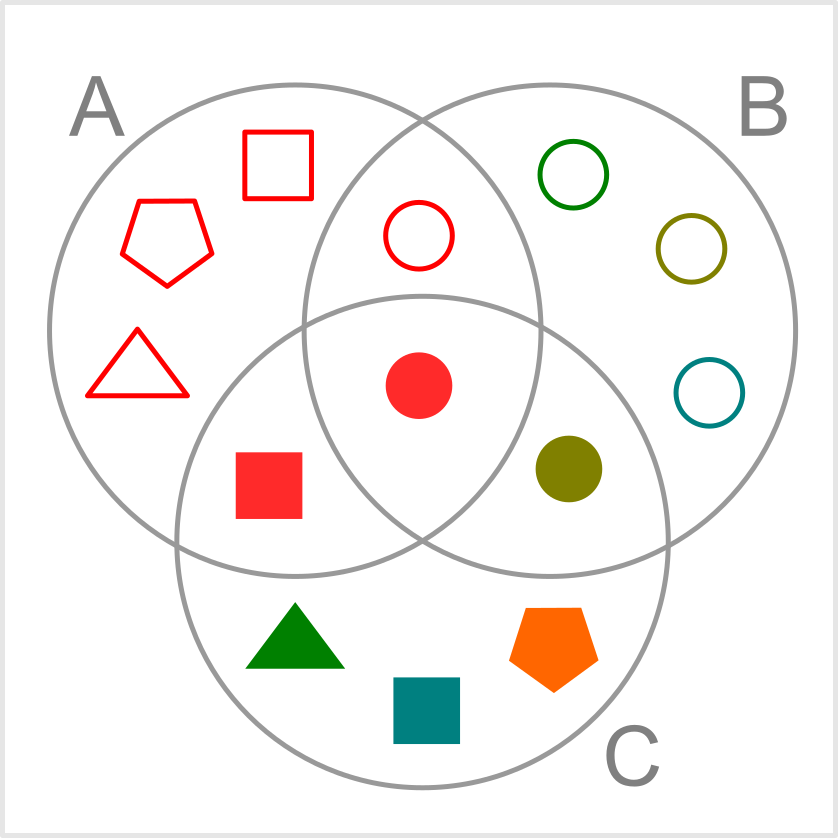
Vennove diagramy využívame napríklad pre názornú ilustráciu množinových operácií. Nasledujúci obrázok ilustruje B \cap (A \cup C):
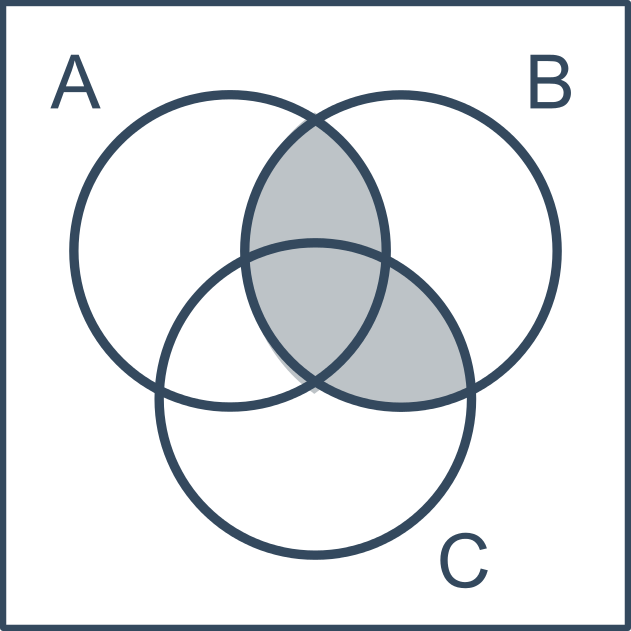
Množiny množín, potenčná množina
Množina prvkom množiny
Prvkom množiny môže byť aj iná množina. S takým prvkom pracujeme rovnako ako s inými prvkami, len sa nesmieme nechať zmiasť.
Príklad: Množina M = \{a, \{b, c, d, e\}, \emptyset\} obsahuje tri prvky:
- „obyčajný“ prvok a
- štvorprvkovú množinu \{b, c, d, e\}
- prázdnu množinu \emptyset
Pozor na rozdiel medzi prázdnou množinou a množinou obsahujúcou prázdnu množinu:
- \emptyset (tiež môžeme písať \{\}) je prázdná množina, jej veľkosť je 0,
- \{\emptyset\} je množina obsahujúca prázdnu množinu, jej veľkosť je 1.
Potenčná množina
Potenčná množina množiny M obsahuje všetky podmnožiny množiny M. Potenčnú množinu značíme \mathcal{P}(M) (existujú aj ďalšie značenia, napríklad 2^M).
Príklad: Pre množinu M = \{a, b, c\} sú všetky jej podmnožiny:
- \{\}
- \{a\}
- \{b\}
- \{c\}
- \{a, b\}
- \{a, c\}
- \{b, c\}
- \{a, b, c\}
Potenčná množina je množina všetkých týchto množín, teda \mathcal{P}(M)=\{\{\}, \{a\}, \{b\}, \{c\}, \{a, b\}, \{a, c\}, \{b, c\}, \{a, b, c\}\}.
Potenčná množina množiny M vždy obsahuje ako svoj prvok samú množinu M. Každá potenčná množina tiež obsahuje ako svoj prvok prázdnu množinu.
Hore
