Trojuholník

Trojuholník je základný geometrický útvar, ktorý má tri vrcholy a tri strany. Trojuholníky hrajú v geometrii kľúčovú rolu, pretože sa veľa problémov dá riešiť tak, že zložitejšie obrazce rozdelíme na trojuholníky a následne pracujeme s nimi.

Značenie strán a uhlov v trojuholníku:

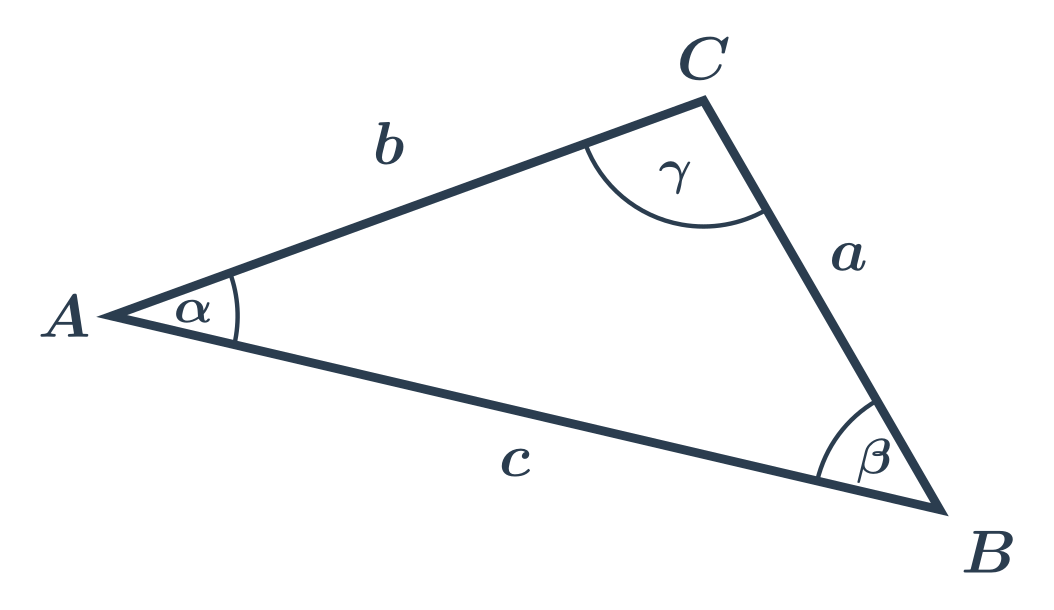
Proti vrcholu A je strana a, proti vrcholu B je strana b a proti vrcholu C je strana c.

Výšky príslušné stranám v trojuholníku:

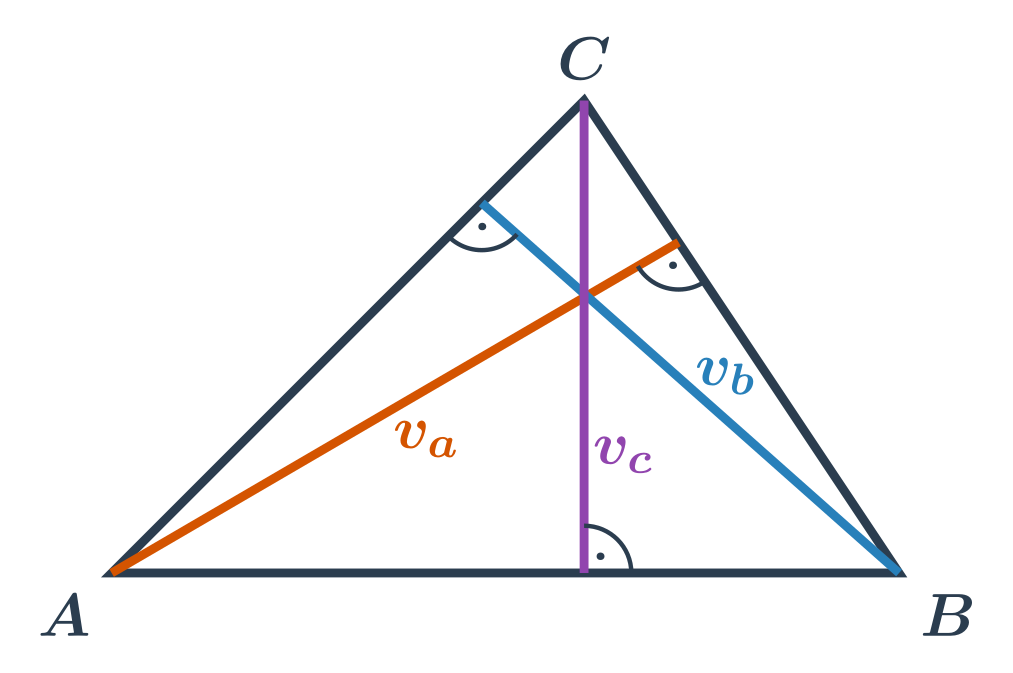
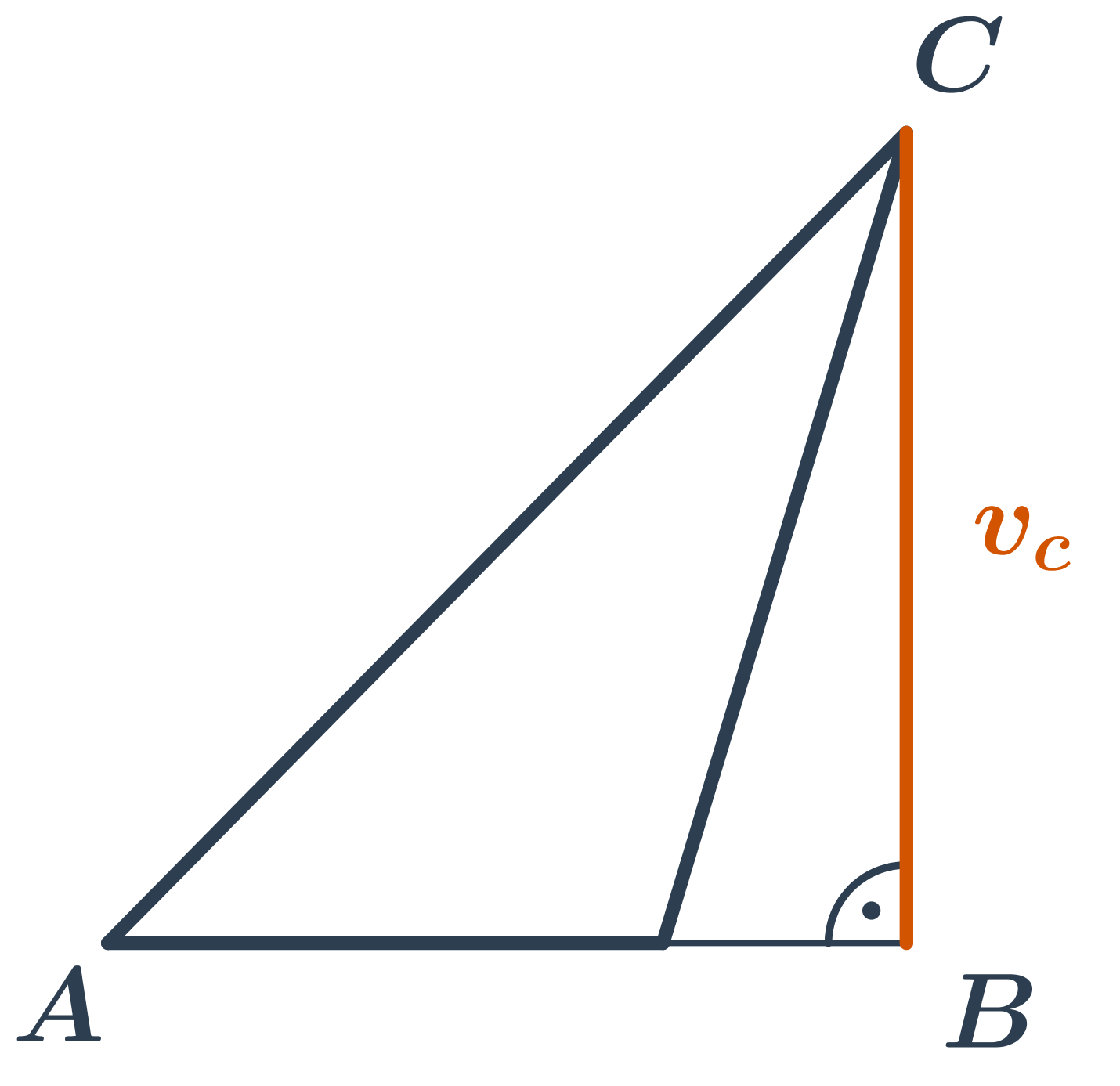
Výška v_a je vzdialenosť bodu A od priamky, na ktorej leží strana a. Teda je to vzdialenosť bodu A od päty kolmice na priamku BC vedenú bodom A. Táto päta kolmice môže a nemusí ležať priamo na strane a.

Témy súvisiace s trojuholníkom:

• Pojmy súvisiace s trojuholníkom (napr. rovnoramenný, rovnostranný, výška, dotyčnica, opísaná kružnica)
• Obvod trojuholníka a obsah trojuholníka (výpočty na základe zadaných údajov o trojuholníku)
• Konštrukčné úlohy s trojuholníkmi (narysovanie trojuholníkov na základe zadaných údajov, napr. s využitím viet sss, sus, usu)
• Pytagorova veta, Euklidove vety, goniometrické funkcie – (užitočné vlastnosti pravouhlého trojuholníka)

Pytagorova veta popisuje vzťah, ktorý platí medzi dĺžkami strán pravouhlého trojuholníka. Veta znie: Obsah štvorca zostrojeného nad preponou pravouhlého trojuholníka je rovný súčtu obsahov štvorcov nad obomi jeho odvesnami. Pytagorovu vetu môžeme zapísať vzťahom c^2 = a^2 + b^2, kde c označuje dĺžku prepony pravouhlého trojuholníka a dĺžky odvesien sú a, b.

Nasledujúci obrázok znázorňuje graficky znenie vety a tiež „obrázkový dôkaz“ tejto vety:

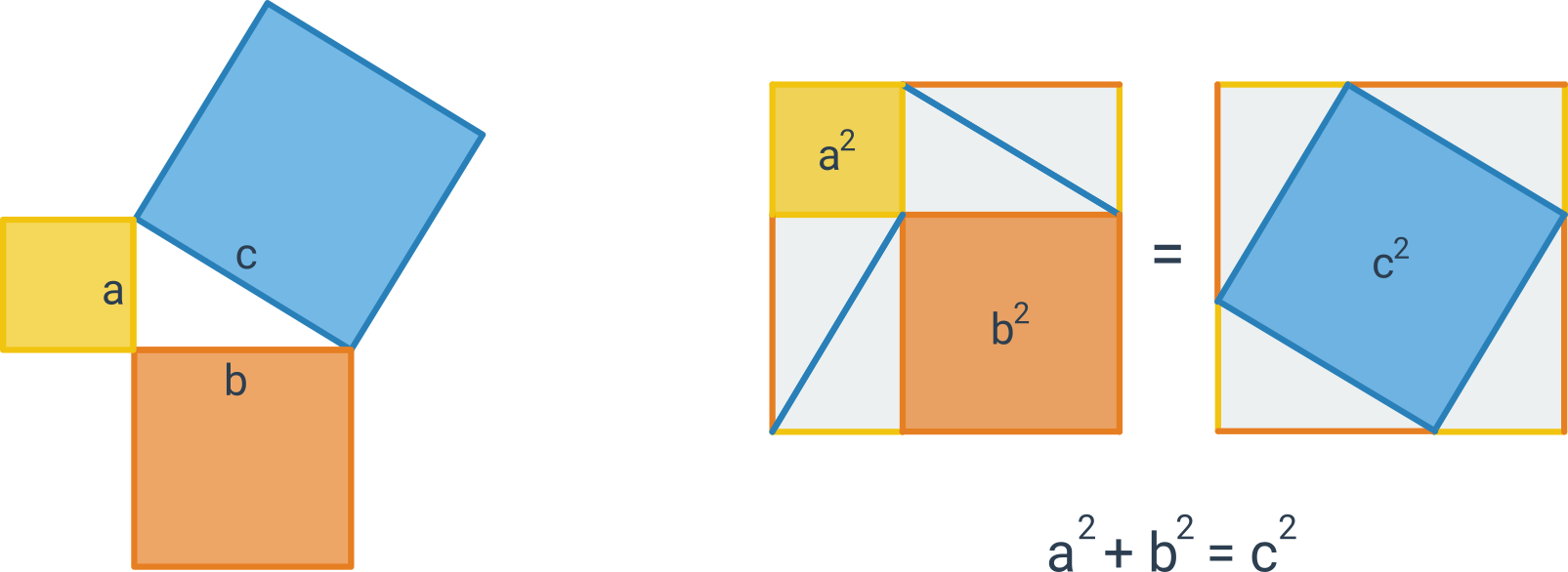
Platí aj opačný smer: Ak má trojuholník strany dĺžok a, b, c, ktoré spĺňajú rovnosť c^2 = a^2 + b^2, potom musí ísť o pravouhlý trojuholník s preponou c.

Pytagorova veta umožňuje dopočítať dĺžku tretej strany pravouhlého trojuholníka, pri ktorom poznáme dĺžky dvoch zvyšných strán:

• Dĺžka odvesny c = \sqrt{a^2 + b^2}. Ak má pravouhlý trojuholník odvesny s dĺžkou 3 metre a 6 metrov, prepona má dĺžku \sqrt{3^2+6^2} = \sqrt{9+36} = \sqrt{45} \doteq 6,41 metra.

• Dĺžka prepony a = \sqrt{c^2-b^2}. Ak má trojuholník preponu s dĺžkou 8 metrov a jedna z odvesien má dĺžku 4 metre, druhá odvesna má dĺžku \sqrt{8^2-4^2} = \sqrt{64-16} = \sqrt{48} \doteq 6,93 metra.

Pytagorejské trojice sú trojice celých čísel, ktoré spĺňajú a^2+b^2=c^2, teda trojuholník s príslušnými dĺžkami strán je pravouhlý. Typickým príkladom pytagorejskej trojice je (3, 4, 5): 3^2 + 4^2 = 9+16 = 25 = 5^2.

Ďalšie príklady pytagorejských trojíc: (5, 12, 13); (8, 15, 17); (7, 24, 25); (20, 21, 29); (9, 40, 41). Medzi pytagorejské trojice patria tiež všetky násobky týchto trojíc, napr. (6, 8, 10); (9, 12, 15); (10, 24, 26). Ak si zapamätáme niektoré základné pytagorejské trojice, predovšetkým najjednoduchšiu trojicu (3, 4, 5), tak nám to môže uľahčiť výpočty.

Pytagorova veta má v geometrii veľmi široké využitie, pretože môžeme veľa zložitejších útvarov rozložiť na pravouhlé trojuholníky.

Typickým príkladom aplikácie Pytagorovej vety je výpočet dĺžky uhlopriečky štvorca alebo výšky rovnostranného trojuholníka:

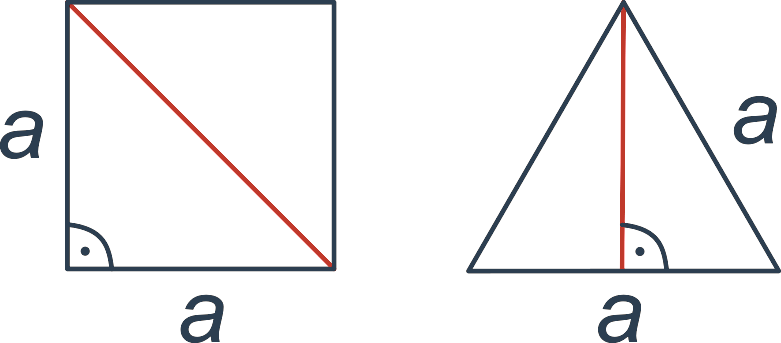
V prípade štvorca so stranou a tvorí uhlopriečka preponu pravouhlého trojuholníka s odvesnami s dĺžkou a. Pre dĺžku uhlopriečky u teda platí u^2 = a^2 + a^2. Po úpravách: u = \sqrt{a^2+a^2} = \sqrt{2a^2} = a\sqrt{2}. Napríklad štvorec so stranou 10 cm má teda uhlopriečku s dĺžkou 10\cdot \sqrt{2} \doteq 14,1 metra.

V prípade rovnostranného trojuholníka so stranou a tvorí výška odvesnu pravouhlého trojuholníka s preponou s dĺžkou a a odvesnou s dĺžkou \frac{a}{2}. Pre dĺžku výšky v teda platí v^2 + \large(\frac{a}{2}\large)^2 = a^2. Po úpravách dostávame v^2 = a^2 - \frac{a^2}{2^2} = \frac{3}{4}a^2, v = a\frac{\sqrt{3}}{2}. Napríklad v rovnostrannom trojuholníku so stranou 5 metrov má teda výška dĺžku \frac{\sqrt{3}}{2}\cdot 5 \doteq 4,33 metra.

Euklidove vety sú dve tvrdenia o vlastnostiach pravouhlého trojuholníka.

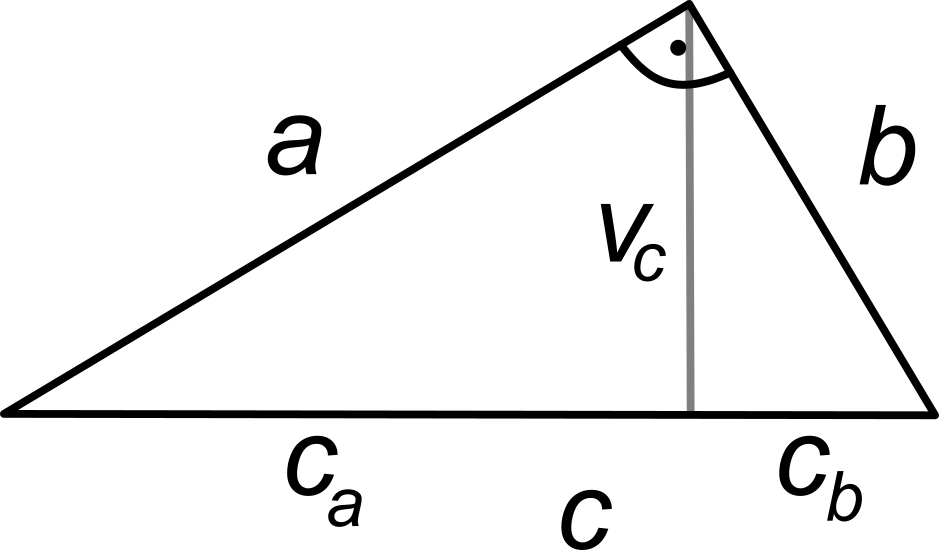
Euklidova veta o výške

Obsah štvorca zostrojeného nad výškou pravouhlého trojuholníka sa rovná obsahu obdĺžnika zostrojeného z oboch úsekov prepony:

v_c^2 = c_a\cdot c_b

Euklidova veta o odvesne

Obsah štvorca zostrojeného nad odvesnou pravouhlého trojuholníka sa rovná obsahu obdĺžnika zostrojeného z prepony a úseku prepony priľahlej k tejto odvesne.

• a^2 = c\cdot c_a
• b^2 = c\cdot c_b