Slovenčina
Angličtina
Informatika
Vieme to
Nemčina
Biológia
Zemepis
Chémia
Aritmetika
Zlomky, percentá, desatinné čísla
Geometria
Elementárna algebra
Funkcie
Jednotky, miery
Diskrétna matematika
Finančná gramotnosť
Rozhodovačka
Pexeso
Počítanie
Grafár
Porozumenie
Označovanie
Presúvanie
Mriežkovaná
Rozdeľovačka
Pokazená kalkulačka
Roboti
Strieľačka
Príšerky
Preteky
Územia
Tipovačka
Tímovka
Predchádzajúce
Cvičenie
Euklidove vety sú dve tvrdenia o vlastnostiach pravouhlého trojuholníka.
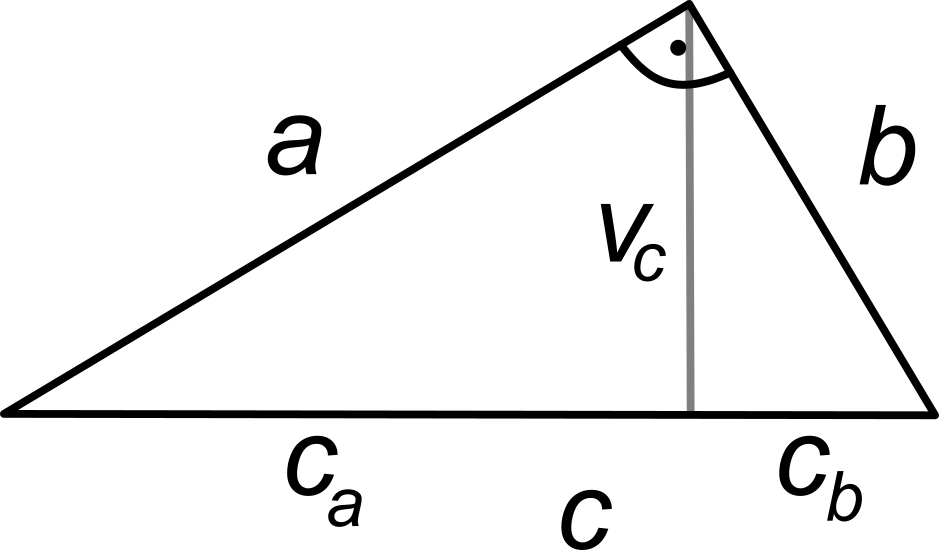
Euklidova veta o výške
Obsah štvorca zostrojeného nad výškou pravouhlého trojuholníka sa rovná obsahu obdĺžnika zostrojeného z oboch úsekov prepony:
v_c^2 = c_a\cdot c_b
Euklidova veta o odvesne
Obsah štvorca zostrojeného nad odvesnou pravouhlého trojuholníka sa rovná obsahu obdĺžnika zostrojeného z prepony a úseku prepony priľahlej k tejto odvesne.
- a^2 = c\cdot c_a
- b^2 = c\cdot c_b
Vysvetlenie mi pomohlo
Vysvetlenie mi nepomohlo
Krok po kroku
Doplňovanie jednotlivých krokov v rozsiahlejšom postupe.
Euklidove vety 
Zobraziť súhrn témy
ťažké
Euklidove vety (ťažké)
Zadaní: 12
Typicky zaberie: 13 min
