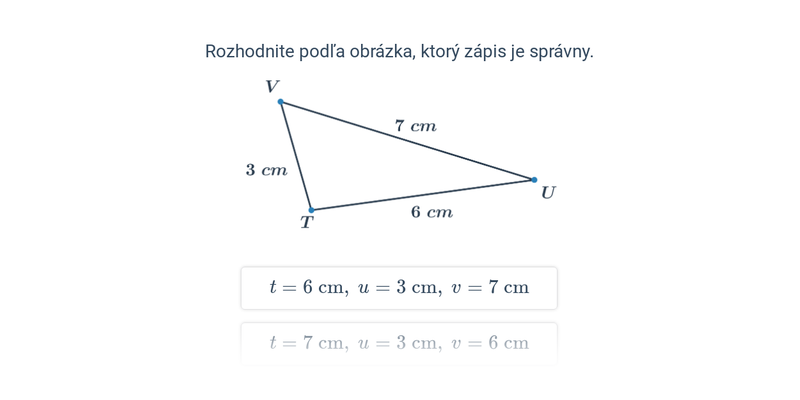
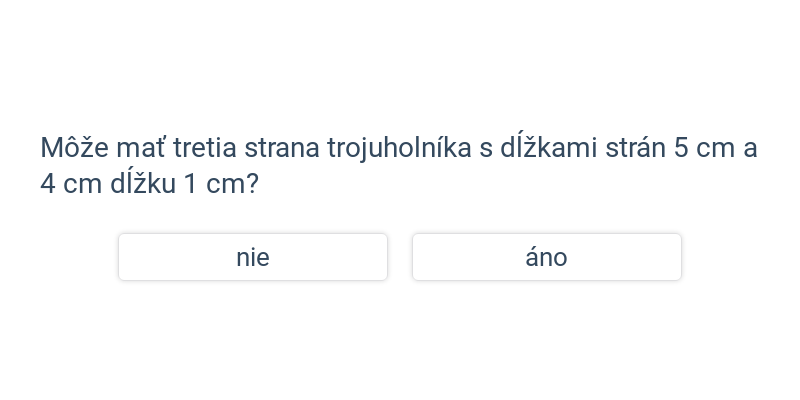
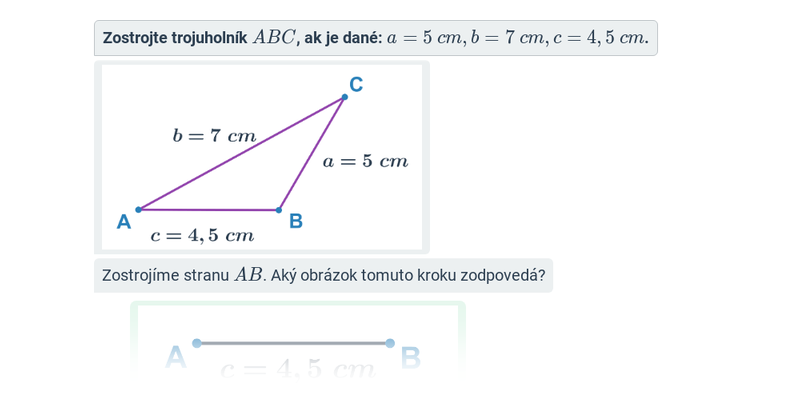
Pri riešení jednoduchších úloh zostrojujeme trojuholníky, pre ktoré poznáme dĺžky strán. Nesmieme pritom zabúdať, že platí tzv. trojuholníková nerovnosť, teda že súčet dvoch strán je väčší než tretia strana. Jednoducho povedané, ak je súčet dvoch najkratších strán väčší než tretia strana, trojuholník sa dá zostrojiť.
Pri zložitejších príkladoch využívame vety o zostrojiteľnosti trojuholníkov (kde s značí stranu a u uhol):
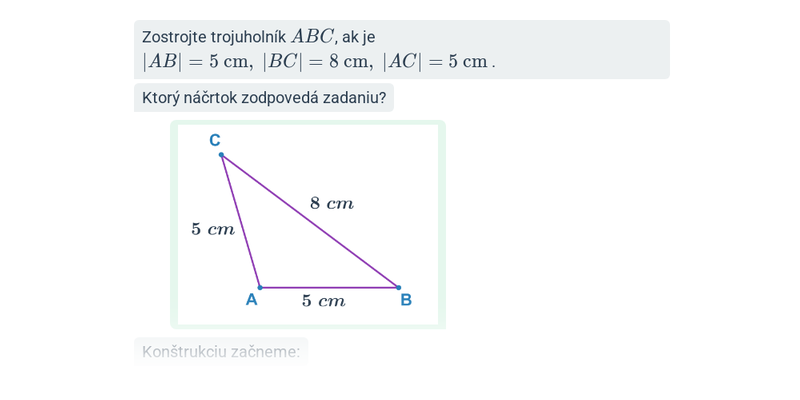
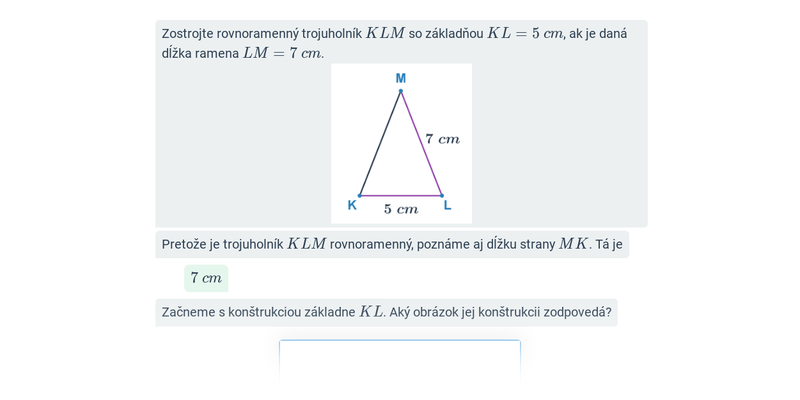
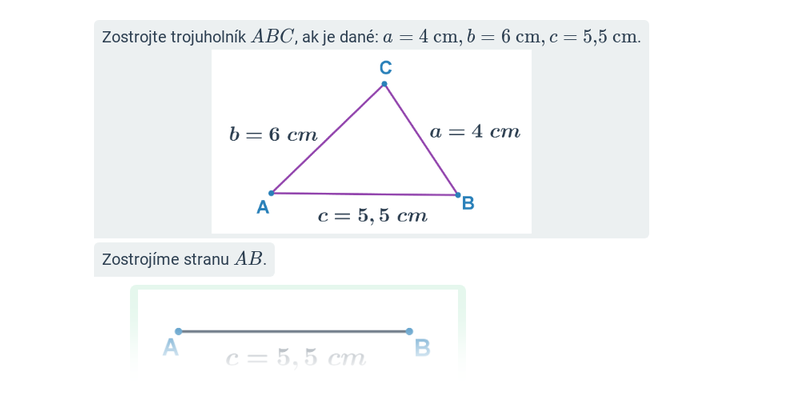
- Veta sss — v trojuholníku sú dané dĺžky všetkých strán, platí trojuholníková nerovnosť.
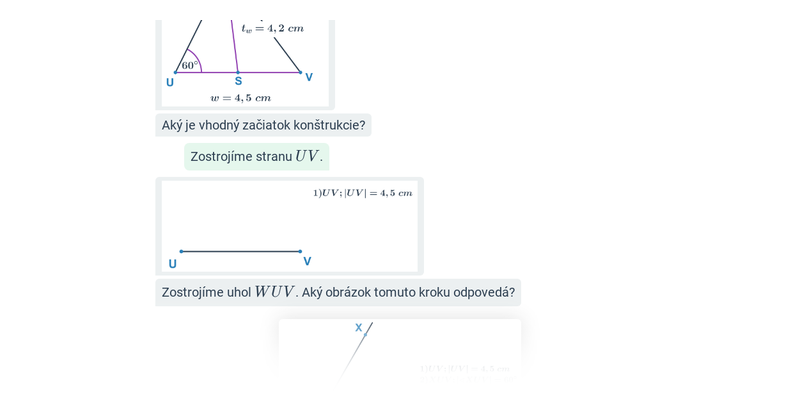
- Veta sus — v trojuholníku sú dané dĺžky dvoch strán a veľkosť uhla, ktorý zvierajú (menší než 180°).
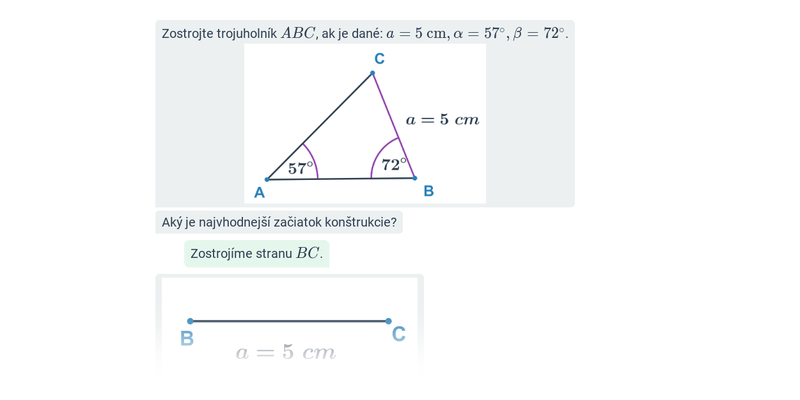
- Veta usu — v trojuholníku je daná dĺžka jednej strany a veľkosti 2 uhlov k nej priliehajúcich (súčet veľkostí daných uhlov je menší než 180°).
Tieto vety tiež používame pri určení zhodnosti trojuholníkov.
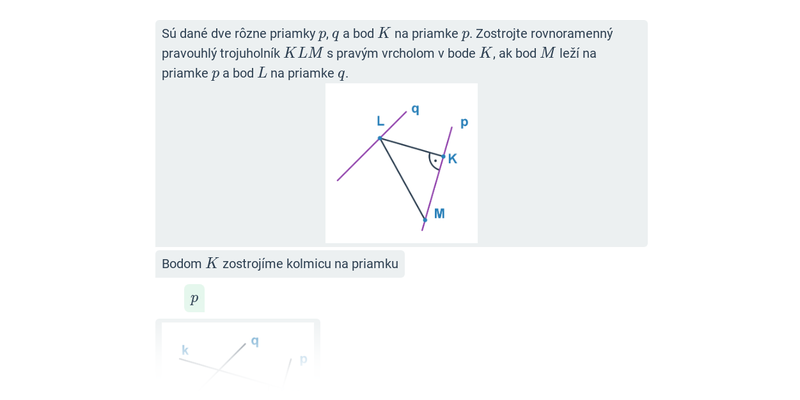
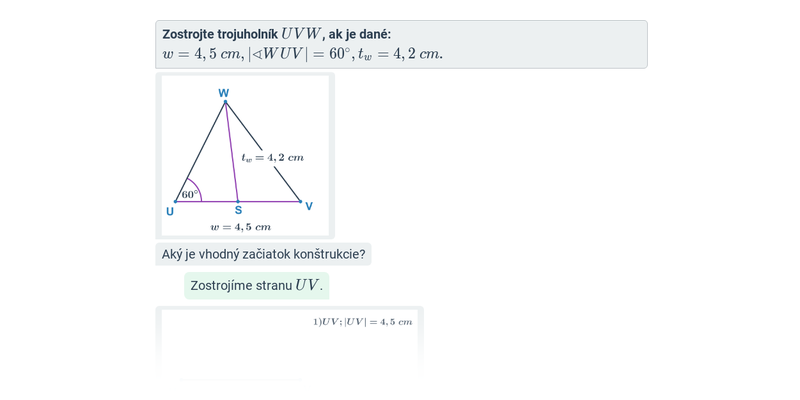
Pri najťažších príkladoch využívame pri konštrukcii ďalšie pojmy súvisiace s trojuholníkom, napríklad výška, ťažnica, či množiny bodov daných vlastností.
Rozhodovačka
Rýchle precvičovanie výberom z dvoch možností.
Krok za krokom
Doplňovanie jednotlivých krokov v rozsiahlejšom postupe.
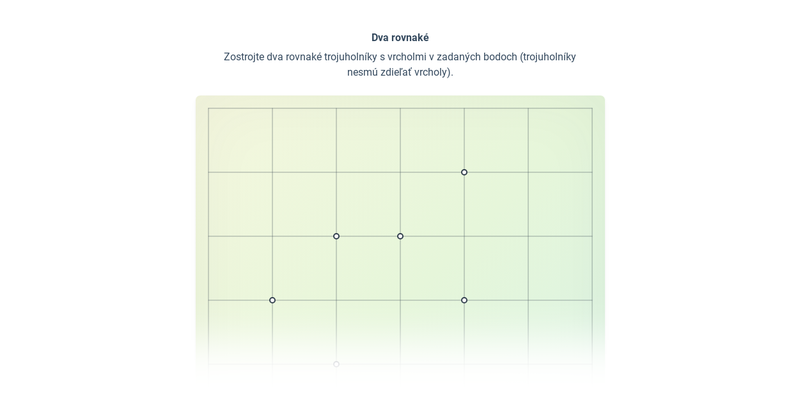
Mriežkovaná
Úloha na precvičenie geometrie s jednoduchým ovládaním a zaujímavými úlohami.