Slovenčina
Angličtina
Informatika
Vieme to
Nemčina
Biológia
Zemepis
Chémia
Fyzika
Aritmetika
Zlomky, percentá, desatinné čísla
Geometria
Elementárna algebra
Funkcie
Jednotky, miery
Diskrétna matematika
Finančná gramotnosť
Rozhodovačka
Pexeso
Krok za krokom
Počítanie
Grafár
Porozumenie
Označovanie
Presúvanie
Mriežkovaná
Rozdeľovačka
Pokazená kalkulačka
Roboti
Strieľačka
Príšerky
Preteky
Územia
Tipovačka
Tímovka
Môj účet
Odhlásiť saVýpis prehľadov
Vektory
Prechádzate súhrny informácií k určitým témam. Systémy Vieme sa zameriavajú hlavne na ich precvičovanie. K cvičeniam k jednotlivým podtémam sa dostanete pomocou odkazov nižšie.
Podkapitoly
Vektor je množina všetkých zhodne orientovaných úsečiek, ktoré majú rovnakú dĺžku. Každú z týchto úsečiek nazývame umiestnením vektora.
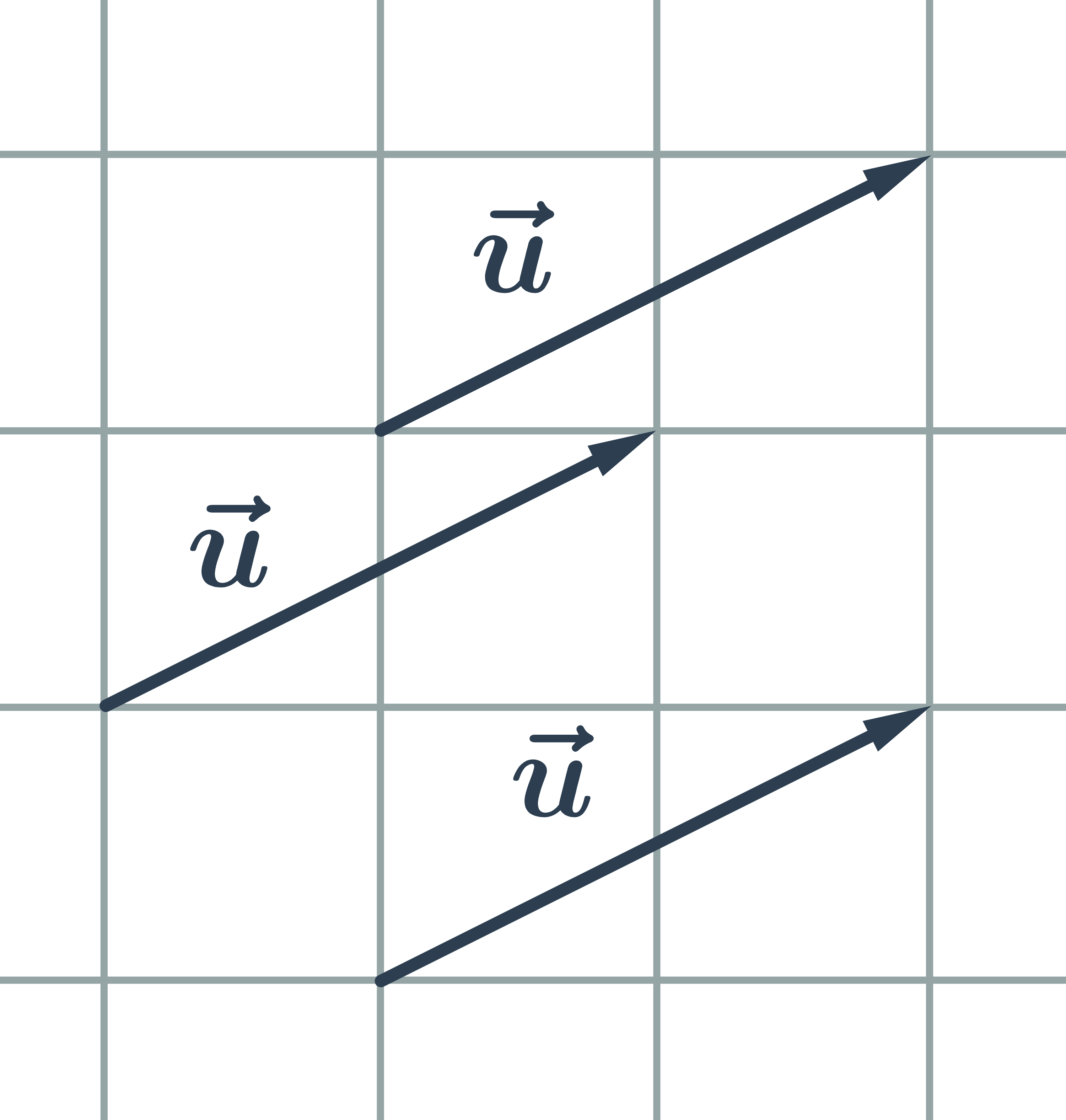
Vektor je určený počiatočným a koncovým bodom, graficky znázorňujeme so šípkou pri koncovom bode, zapisujeme: \vec{u}=\overrightarrow{AB}
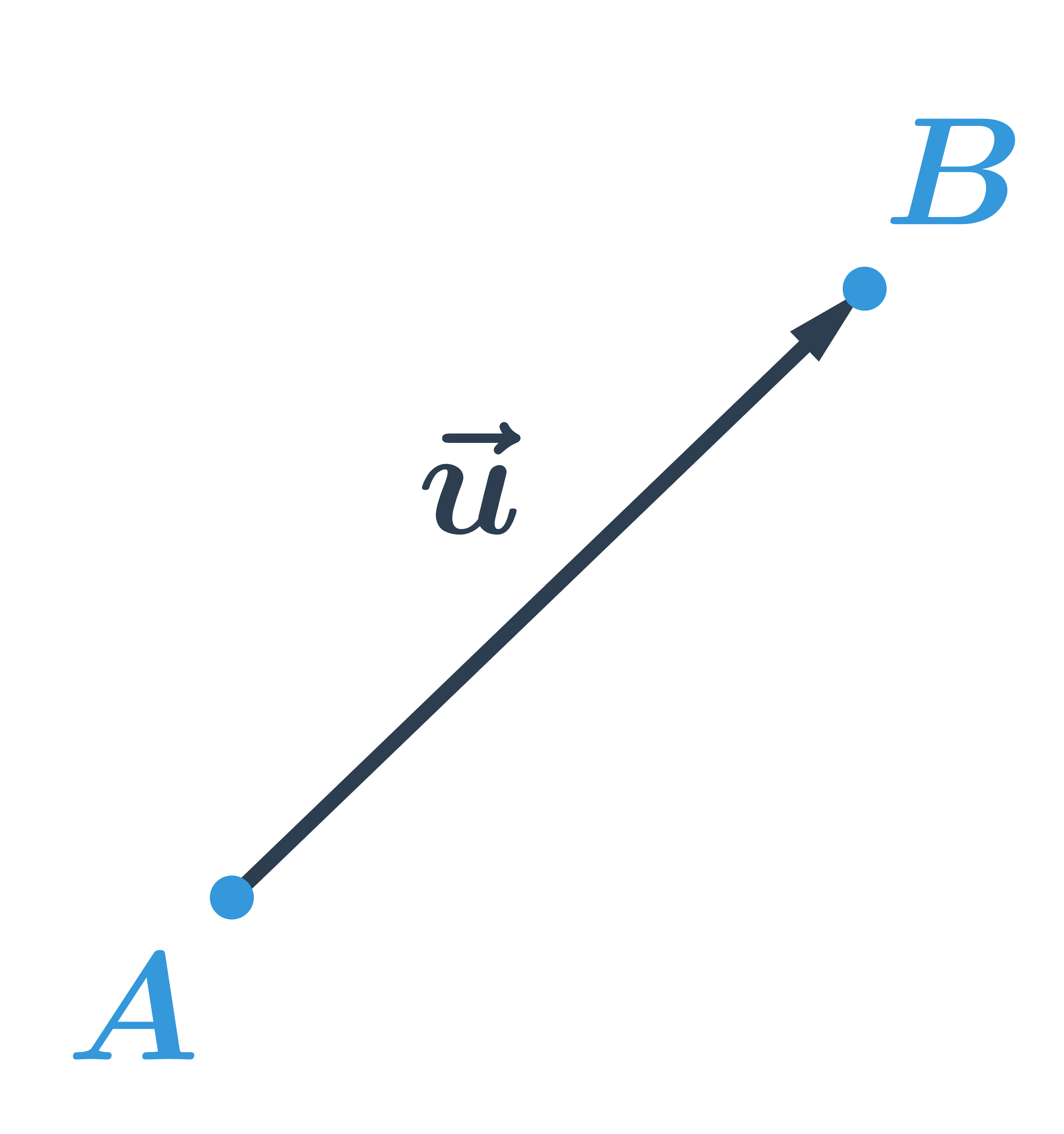
Na obrázku je A počiatočný bod vektora \vec{u}, B je koncový bod vektora \vec{u}.
HoreVektory: pojmy
Opačné vektory sú vektory, ktoré majú rovnakú dĺžku a opačnú orientáciu:
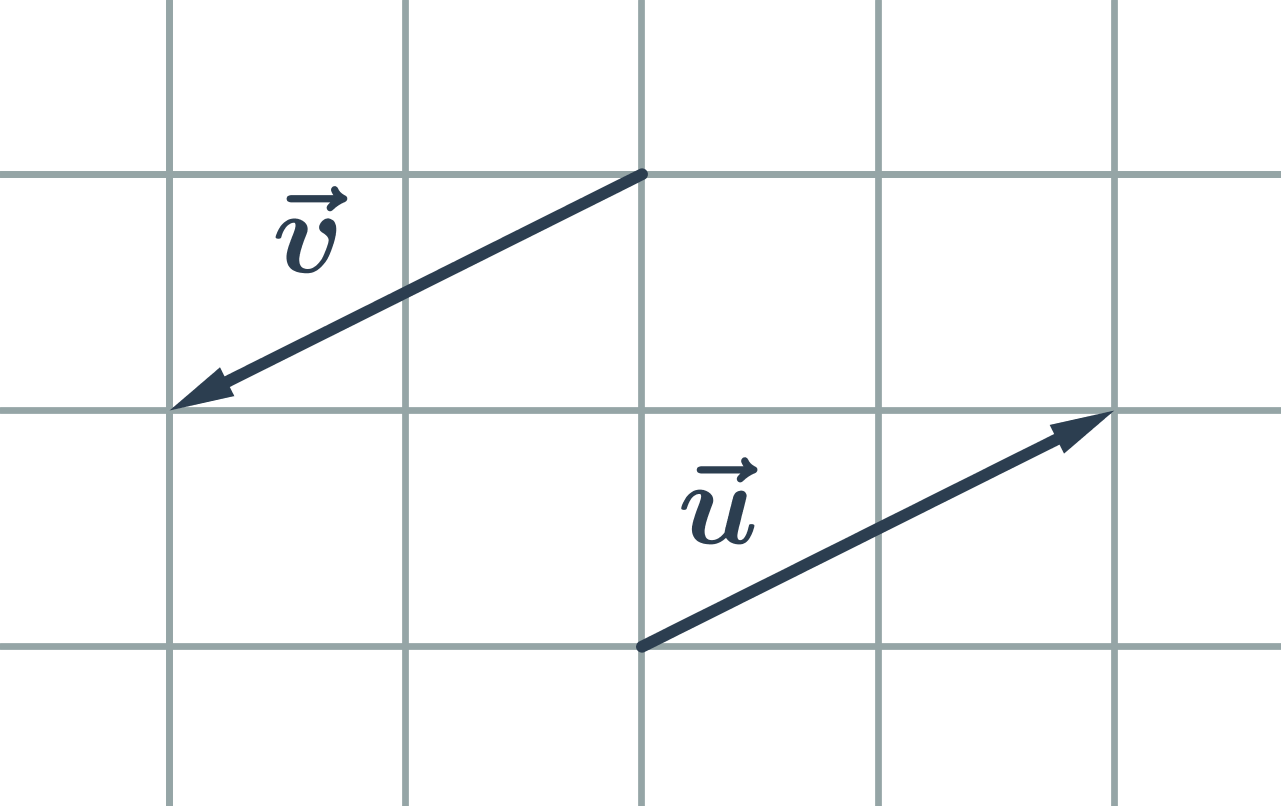
Kolineárne vektory sú vektory, ktoré môžeme umiestniť na jednu priamku. Teda nemusia mať rovnakú dĺžku, môžu mať rovnakú alebo opačnú orientáciu:
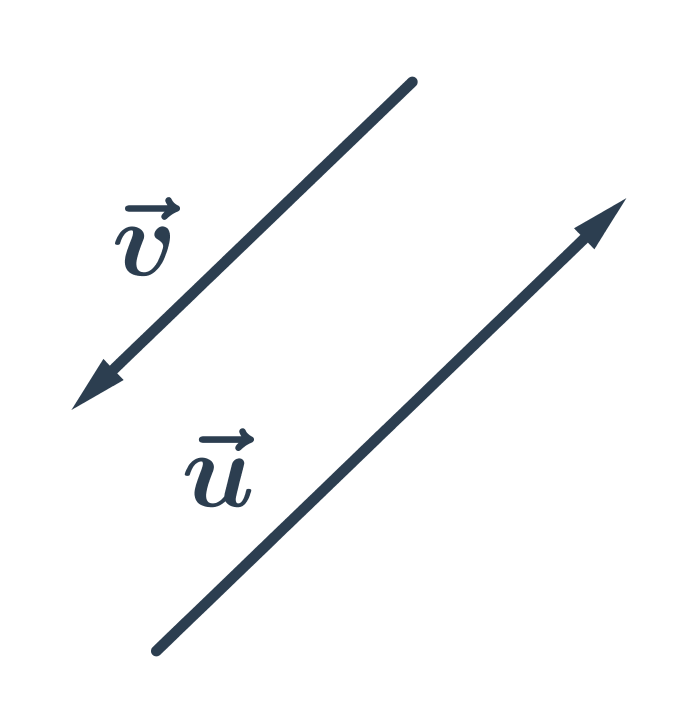
Kolmé vektory sú vektory, ktoré zvierajú pravý uhol:
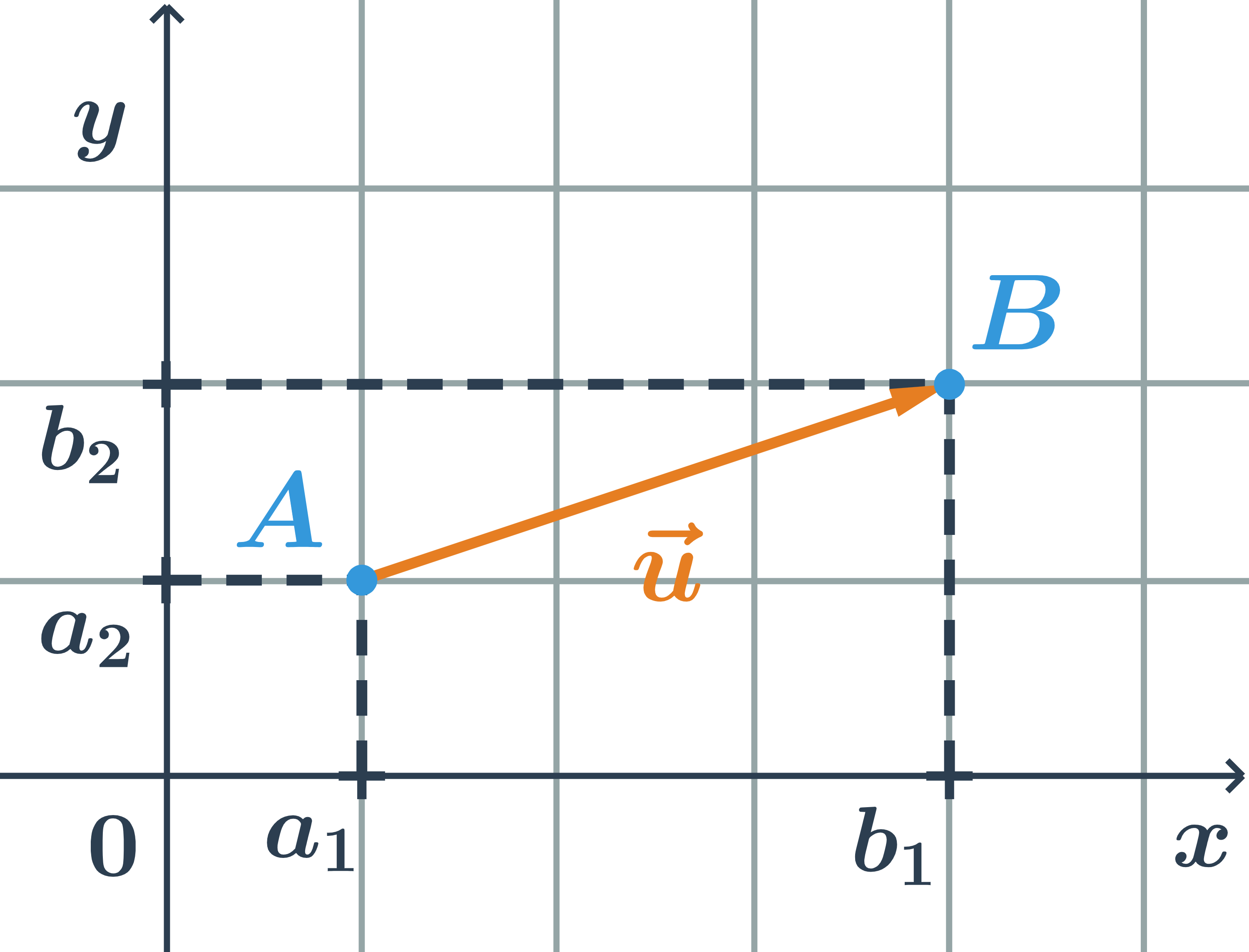
Súradnice vektora sú pravouhlé priemety vektora do súradných osí, teda vektor \vec{u}=\overrightarrow{AB} má súradnice: \vec{u}=(u_1;u_2)=(b_1-a_1;b_2-a_2)
Veľkosť vektora \vec {u}=\overrightarrow{AB} je dĺžka úsečky AB, značíme \left| \vec{u} \right| a platí: \left| \vec{u} \right|=\sqrt{u_1^2+u_2^2}
Jednotkový vektor má dĺžku 1.
Nulový vektor má nulovú dĺžku, teda splýva jeho počiatočný a koncový bod.
HoreSúradnice vektorov
Už vieme, že vektor je množina nekonečne veľa orientovaných úsečiek, jedna z nich má počiatok v počiatku súradného systému, v bode O=[0;0]. Súradnice koncového bodu sú súradnice daného vektora.
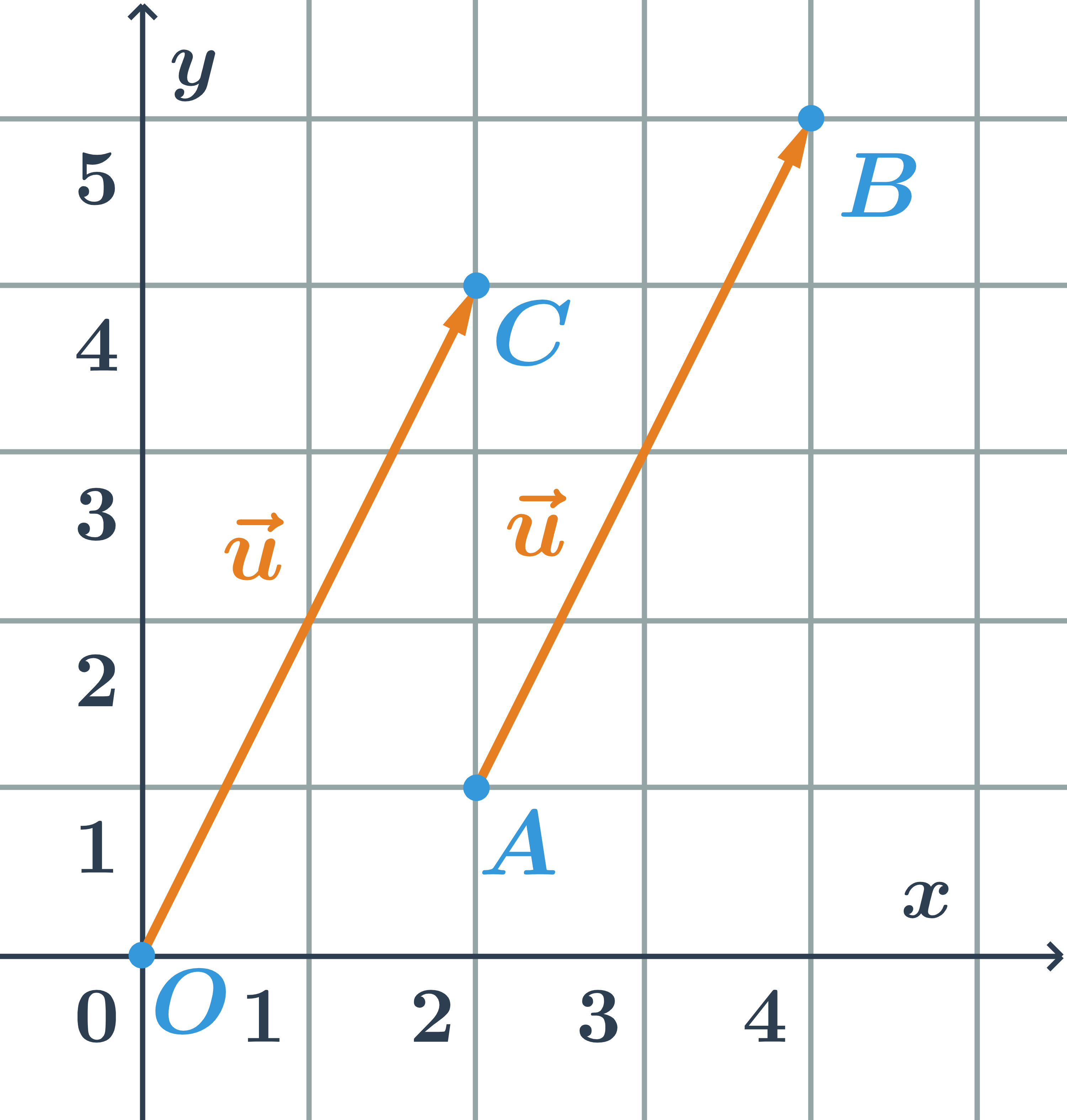
Súradnice vektora \overrightarrow{AB}
- Ak chceme vektor \overrightarrow{AB} posunúť do počiatku súradného systému, posunieme ho o dva štvorčeky vľavo a o jeden štvorček dole.
- Bod A sa posunie do bodu O, bod B sa posunie do bodu C. Tento posun môžeme vyjadriť takto:
- A sa posunie na [2-2;1-1]=[0;0]
- B sa posunie na [4-2;5-1]=[2;4]
- Súradnice vektora na obrázku sú: \vec{u}=\overrightarrow{AB}=\overrightarrow{OC}=(2;4)
Všimnite si, že súradnice vektora \overrightarrow{AB} sme získali odčítaním súradníc bodu A od súradníc bodu B
Pre súradnice vektora \overrightarrow{AB} určeného bodmi A=[a_1;a_2], B=[b_1;b_2] platí: \overrightarrow{AB}=B-A=(b_1-a_1;b_2-a_2)
HoreVeľkosť vektorov
Veľkosť vektora \overrightarrow{AB} je dĺžka úsečky AB. Vektor, ktorý má dĺžku 1, sa nazýva jednotkový vektor:
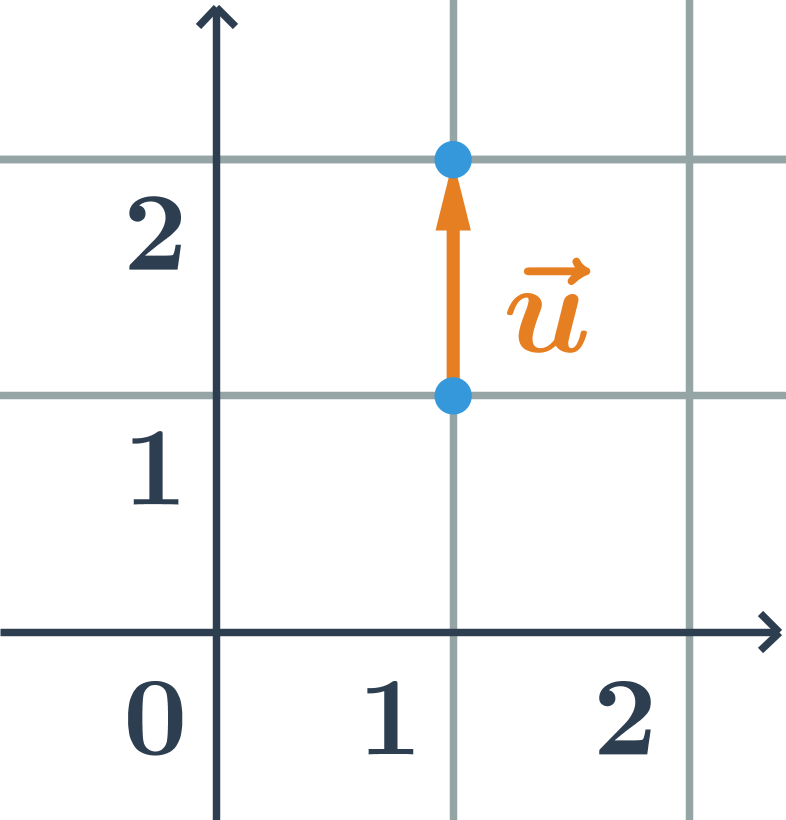
Vektor, ktorý má nulovú dĺžku (počiatočný a koncový bod vektora splýva) sa nazýva nulový vektor:
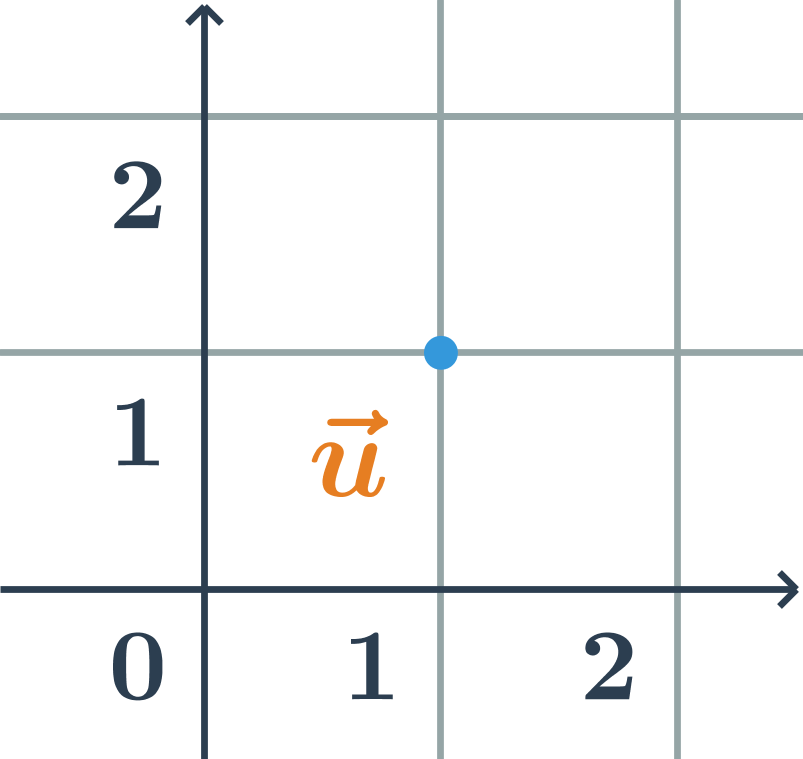
Veľkosť vektora \vec{u}=(u_1;u_2) určíme s využitím Pytagorovej vety: \left| \vec{u} \right|=\sqrt{u_1^2+u_2^2}
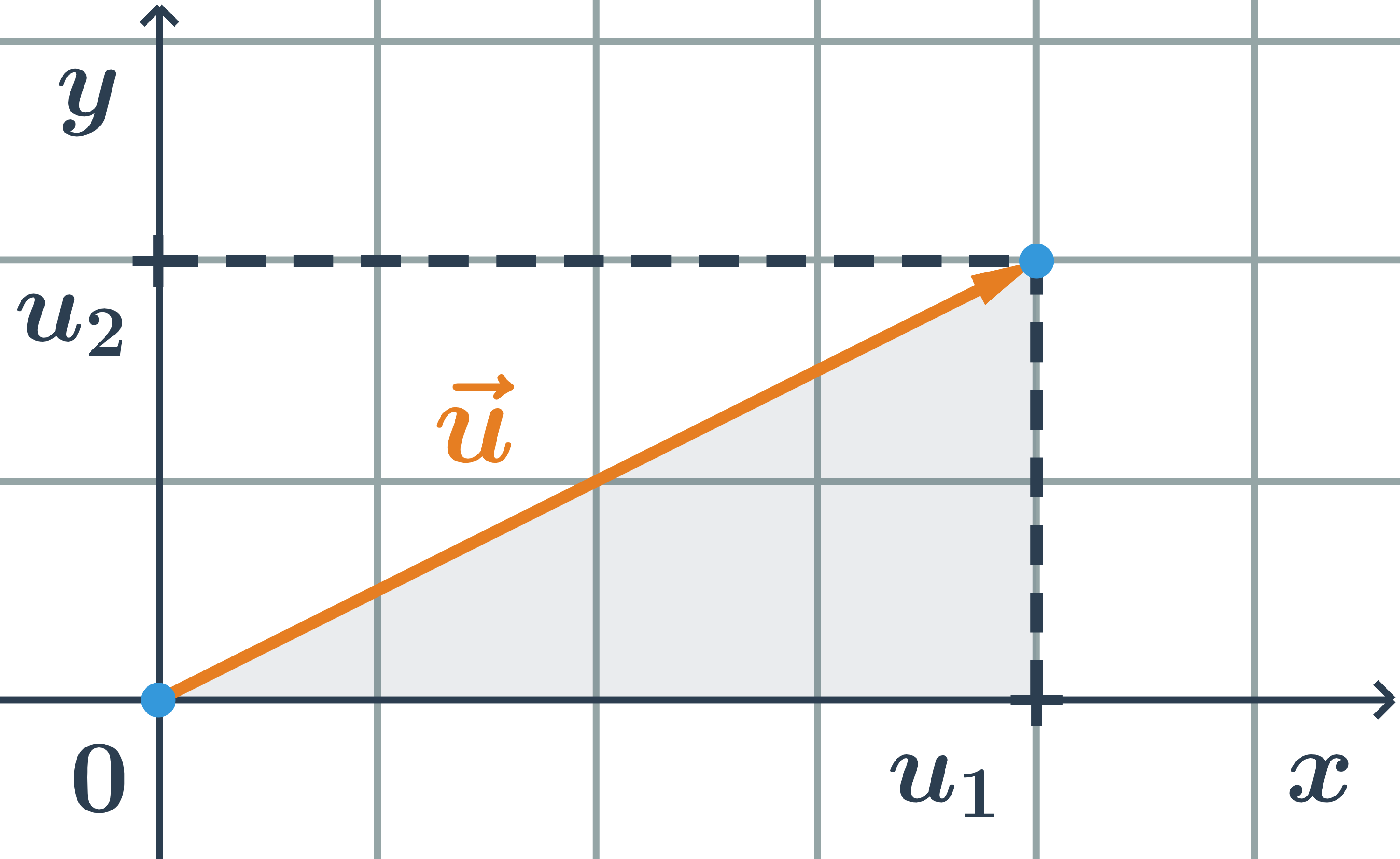
Vo vyfarbenom trojuholníku je dĺžka vektora prepona, odvesny majú dĺžky u_1 a u_2.
Príklad: veľkosť vektora
Určite veľkosť vektora na obrázku:
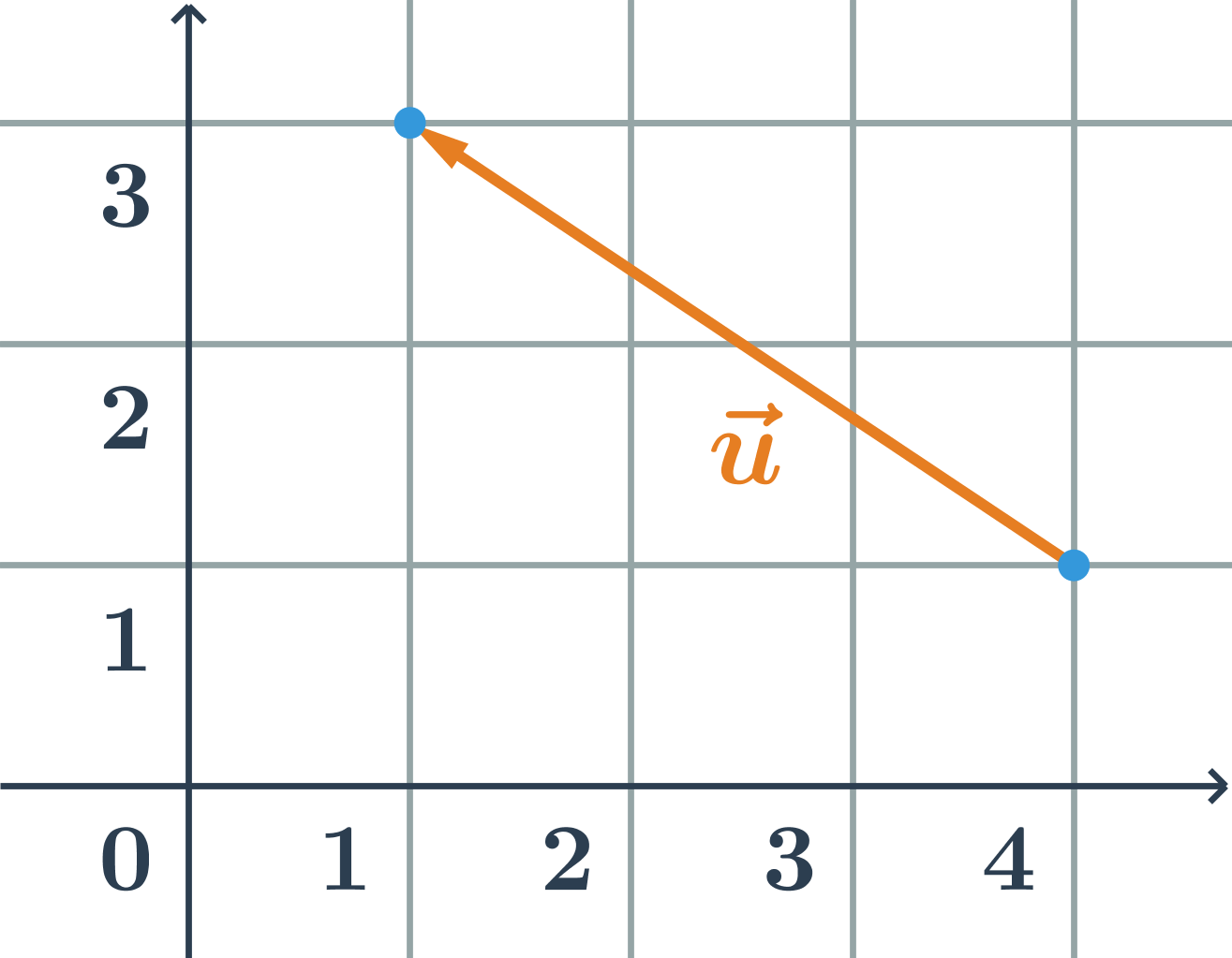
Vektor na obrázku má súradnice \vec{u}=(-3;2), jeho veľkosť je \left| \vec{u} \right|=\sqrt{(-3)^2+2^2}=\sqrt{(-3)^2+2^2}=\sqrt{13}
Vzájomná poloha vektorov
Opačné vektory sú vektory, ktoré majú rovnakú dĺžku a opačnú orientáciu. K vektoru \vec{u}=(u_1;u_2) je opačný vektor \vec{v}=(-u_1;-u_2)
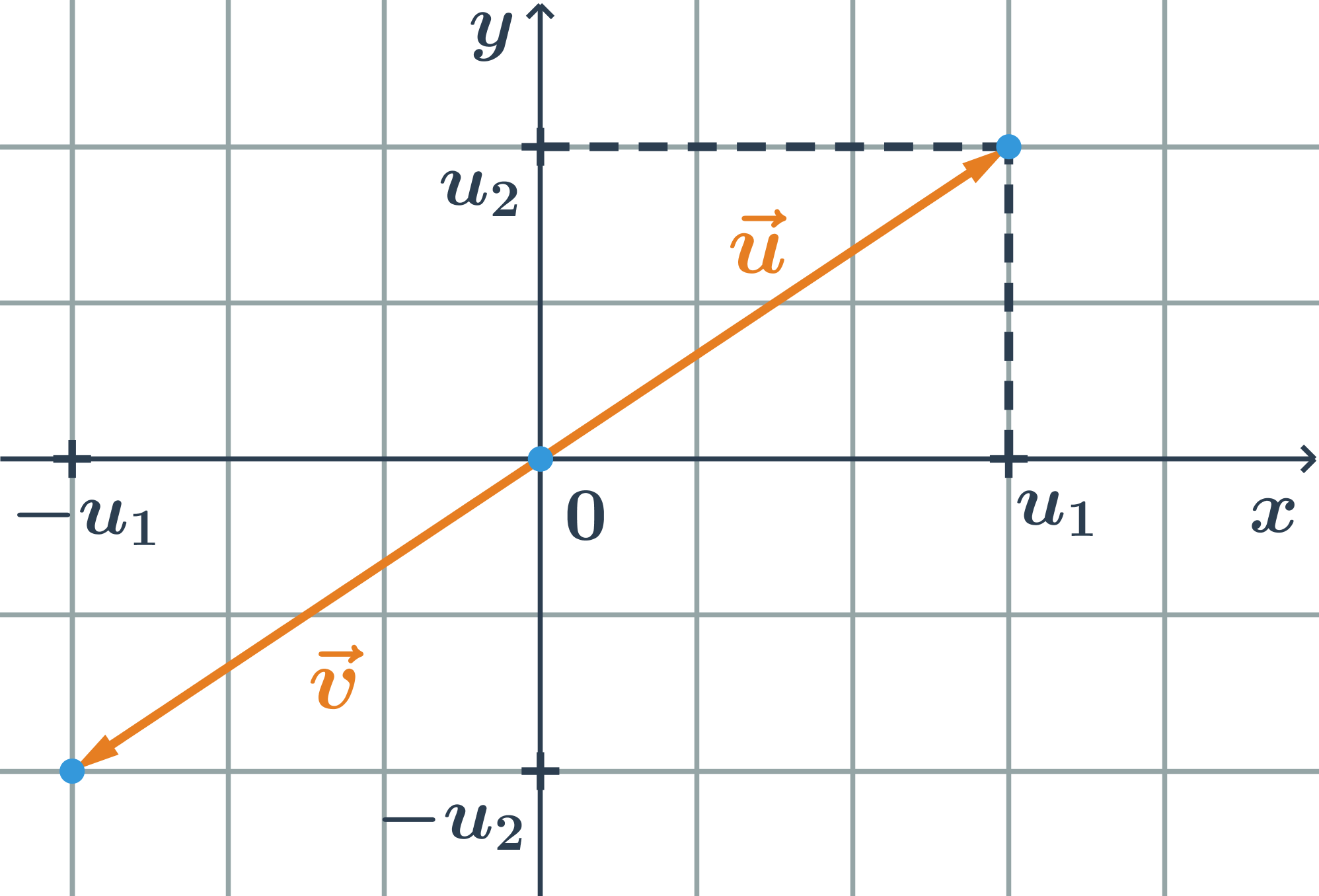
Príklad opačný vektor
- Určite opačný vektor k vektoru \vec{u}=(3;-1).
- Opačný vektor \vec{v} k vektoru \vec{u} má súradnice: (-u_1;-u_2)=(-3;1)
Kolineárne vektory sú vektory, ktoré môžeme umiestniť na jednu priamku. S vektorom \vec{u}=(u_1;u_2) je kolineárny každý vektor \vec{v}=(k\cdot u_1;k \cdot u_2), kde k je reálne nenulové číslo. Pre k>0 majú vektory rovnaký smer, pre k<0 majú vektory opačný smer.
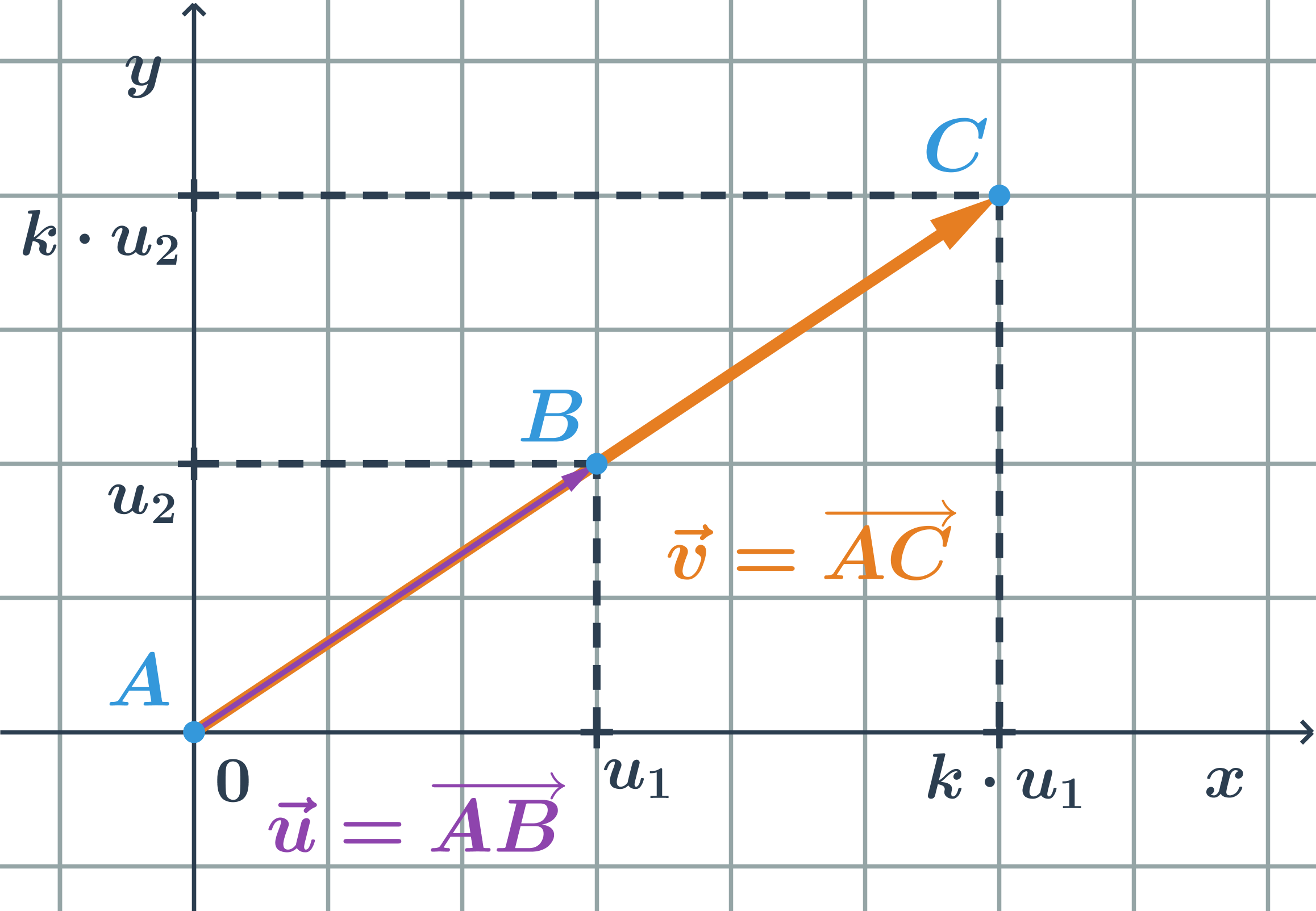
Príklad kolineárny vektor
- Doplňte súradnicu vektora \vec{v}=(v_1;3) tak, aby bol kolineárny s vektorom \vec{u}=(2;-1).
- Pre druhú súradnicu platí: v_2=3, u_2=-1, teda v_2= (-3) \cdot u_2
- Vidíme, že k=-3 je záporné, teda \vec{u} a \vec{v} majú opačnú orientáciu
- Pre prvú súradnicu musí platiť: v_1= (-3) \cdot u_1= (-3)\cdot2=-6.
Kolmé vektory sú vektory, ktoré zvierajú pravý uhol Na vektor \vec{u}=(u_1;u_2) je kolmý každý vektor \vec{v}=(-k\cdot u_2;k \cdot u_1), kde k je reálne nenulové číslo.
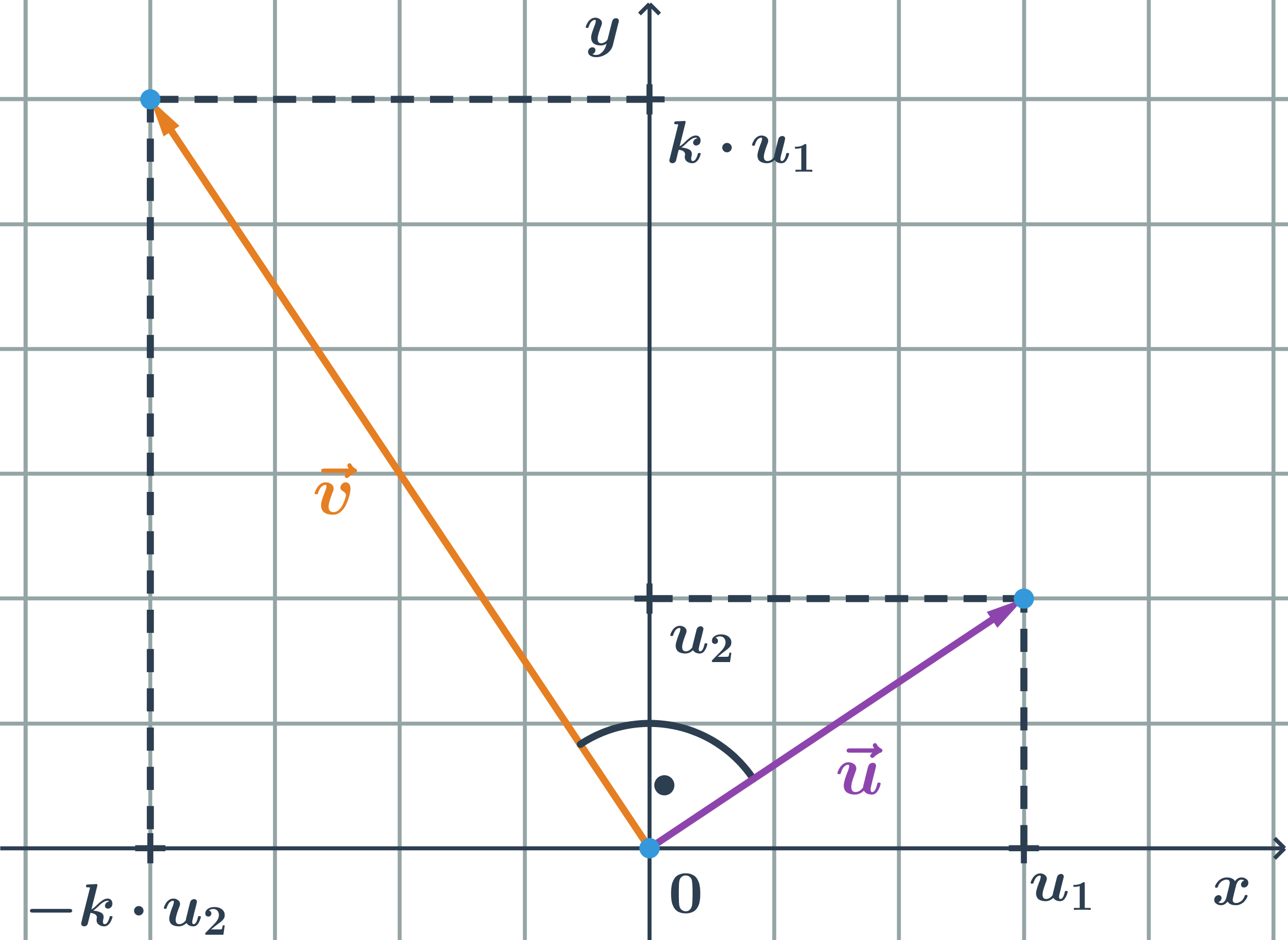
Príklad kolmý vektor
- Doplňte súradnicu vektora \vec{v}=(v_1;4) tak, aby bol kolmý k vektoru \vec{u}=(2;-1).
- Platí: v_2=2 \cdot u_1, teda musí platiť: v_1 = - 2 \cdot u_2.
- Máme teda v_1 = - 2 \cdot u_2 = -2 \cdot (-1) = 2.
