Zlomky: základy

Zlomky zapisujeme v tvare \frac{a}{b}, kde a sa nazýva čitateľ a b menovateľ. Aby mal zlomok zmysel, nesmie byť menovateľ nula. Význam zlomku zodpovedá deleniu. Príklad: v zlomku \frac32 je čitateľom číslo 3 a menovateľom číslo 2, hodnota zlomku \frac32 sa rovná deleniu 3:2 = 1{,}5 („jedna a pol“).

Zlomok \frac{a}{b} je v základnom tvare, ak sú čísla a, b nesúdeliteľné (teda ich jediný kladný spoločný deliteľ je číslo 1). Na základný tvar prevádzame zlomky pomocou krátenia. Príklady:

• Zlomok \frac64 nie je v základnom tvare, pretože čísla 6 a 4 sú súdeliteľné – majú spoločný deliteľ 2, ktorým je možné zlomok krátiť, čím dostávame základný tvar \frac32.
• Zlomok \frac34 je v základnom tvare, pretože čísla 3 a 4 sú nesúdeliteľné.

Základy práce so zlomkami si môžete precvičiť v týchto témach:

• Určovanie zlomkov
• Zlomky na číselnej osi
• Porovnávanie zlomkov
• Zmiešané čísla

Zlomky vyjadrujú „časti z celku“. Môžeme ich graficky vyjadriť mnohými spôsobmi:

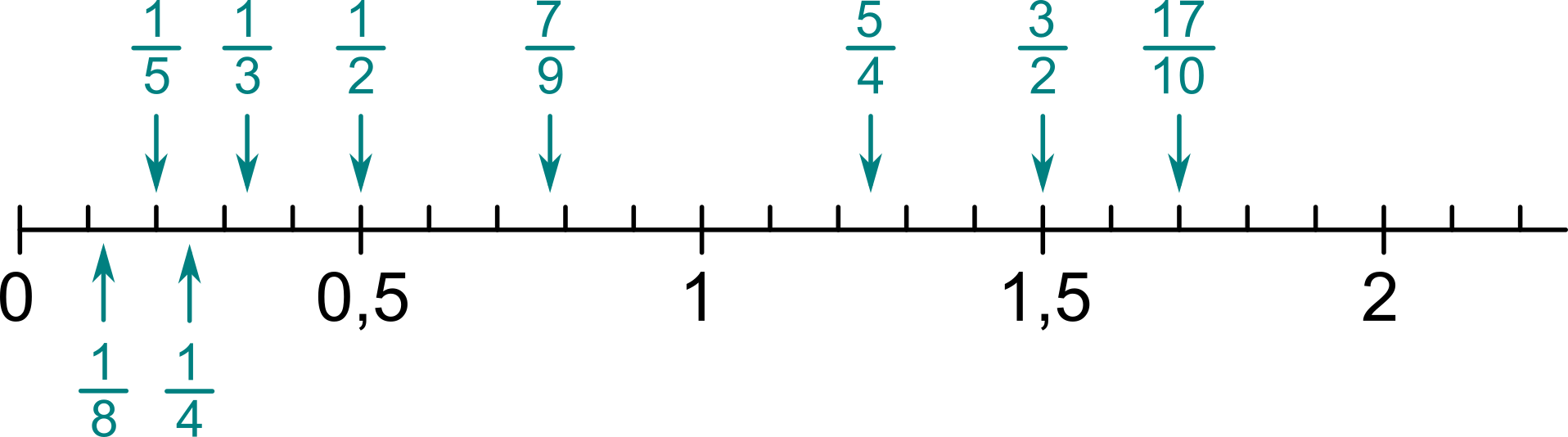
Zlomok môžeme na číselnú os umiestniť tak, že ho prevedieme na desatinné číslo (vydelíme jednoducho čitateľ menovateľom) a potom postupujeme rovnako ako pri desatinných číslach. Napríklad \frac{6}{5} = 1{,}2, teda zlomok \frac{6}{5} leží dve desatiny za jednotkou. Ďalšie príklady:

Zlomky menšie než 1 môžeme umiestňovať na číselnú os tiež priamo (bez prevodu na desatinné číslo) vďaka predstave „časť z celku“. Ak máme umiestniť zlomok \frac{3}{7}, predstavíme si, ako by sme rozdelili úsečku od 0 po 1 na sedem rovnakých častí. Zlomok \frac{3}{7} potom umiestnime na tretiu pozíciu.

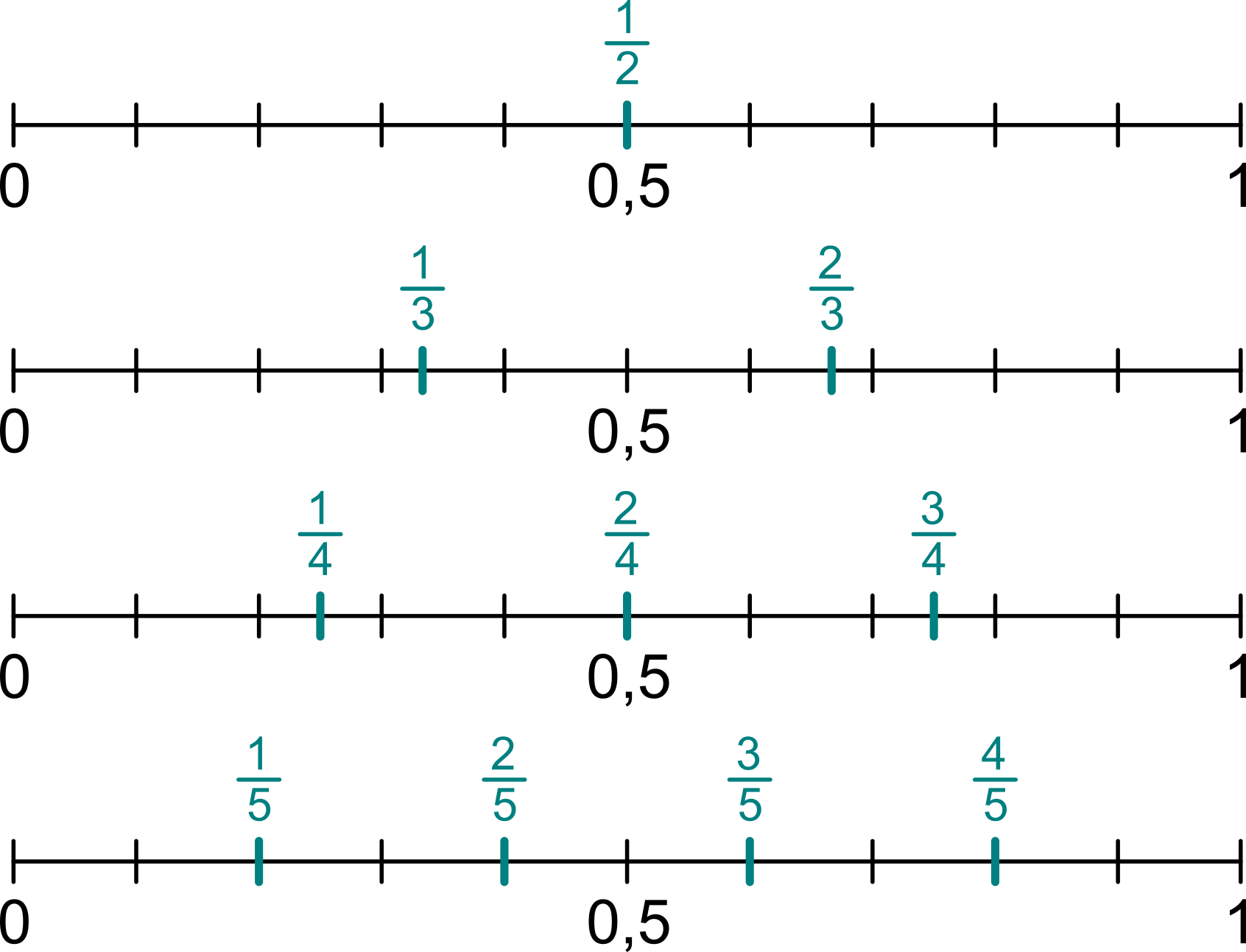
Hodí sa si vybudovať dobrú predstavu hlavne pre zlomky s malým menovateľom:

Než sa pustíme do porovnávania zlomkov, je dobré mať jasno v tom, čo je čitateľ („to hore“) a menovateľ („to dole“). V zlomku \frac{3}{7} je 3 čitateľ, 7 menovateľ.

Porovnávanie zlomkov s rovnakým menovateľom

Porovnávania zlomkov s rovnakým menovateľom je jednoduché: stačí jednoducho porovnať čitatele. Ak napríklad porovnávame zlomky \frac{3}{7} a \frac{5}{7}, je väčší druhý zlomok. Oba zlomky vyjadrujú sedminy z celku a je jednoducho viac, keď máme sedmín päť.

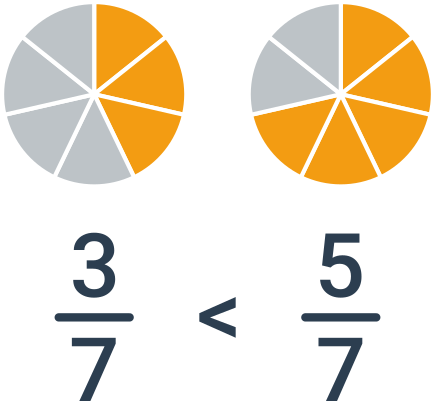
Porovnávanie zlomkov s rovnakým čitateľom

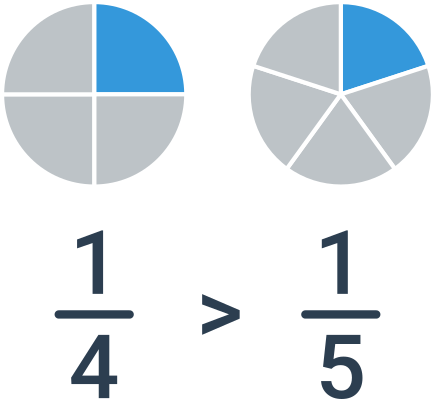
Ak majú zlomky rovnaký čitateľ, potom stačí porovnať menovatele. V tomto prípade je ale poradie zlomkov opačné než poradie menovateľov. Ak porovnávame napríklad zlomky \frac{1}{4} a \frac{1}{5}, je väčšia jedna štvrtina: dostanem väčší kúsok pizzy, ak sa bude deliť medzi 4 ľudí, než keď sa bude deliť medzi 5 ľudí.

Odlišný menovateľ aj čitateľ

V tomto prípade potrebujeme zlomky najskôr previesť na spoločný menovateľ a až potom vykonať porovnanie podľa čitateľov. Príklad: porovnanie zlomkov \frac{2}{3} a \frac{4}{7}. Najmenší spoločný menovateľ je 21, po rozšírení dostávame dvojicu zlomkov \frac{2}{3}=\frac{2\cdot 7}{3\cdot 7}=\frac{14}{21} a \frac{4}{7}=\frac{4\cdot 3}{7\cdot 3}=\frac{12}{21}. Pretože 14 > 12, je väčší prvý zlomok, tj. \frac{2}{3}.

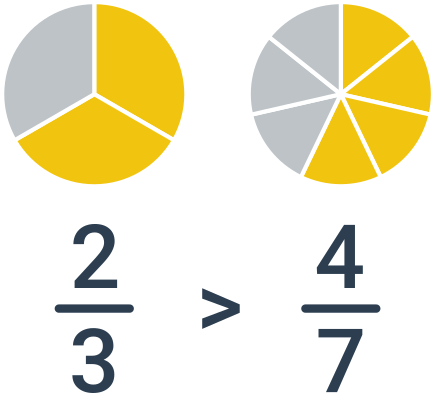
Porovnanie bez výpočtu

Často môžeme vykonať porovnanie aj bez detailného výpočtu, ak si zlomky správne predstavíme alebo porovnáme s vhodnou hodnotou „medzi“:

• Zlomky \frac{2}{3} a \frac{7}{6}. Prvý z nich je menší než 1, druhý je väčší než 1. Platí teda \frac{2}{3} < \frac{7}{6}.

• Zlomky \frac{1}{3} a \frac{4}{5}. Prvý z nich je určite menší než polovica, druhý je výrazne väčší než polovica. Platí teda \frac{1}{3} < \frac{4}{5}.

Ak má zlomok menovateľ väčší než čitateľ (zlomok je menší než jedna), označuje sa zlomok ako pravý. Nepravé zlomky (teda tie, ktoré sú väčšie ako jedna) môžeme zapísať pomocou zmiešaného čísla. Zmiešané číslo a\frac{b}{c} je zápis súčtu a + \frac{b}{c}, kde \frac{b}{c} je kladný zlomok menší než jedna. Príklady:

• 1\frac{1}{2} = \frac{3}{2}
• 2\frac{3}{5} = \frac{13}{5}

Prevod zmiešaného čísla na zlomok urobíme na základe pozorovania, že jednotku môžeme zapísať ako \frac{c}{c}. Príklad: 3\frac14 = 3\cdot\frac44 + \frac14 = \frac{12}{4}+\frac14 = \frac{13}{4}.

Prevod nepravého zlomku na zmiešané číslo urobíme pomocou delenia so zvyškom. Celá časť zmiešaného čísla zodpovedá podielu, čitateľ zvyšného zlomku zodpovedá zvyšku. Príklad:

• \frac{17}{3} = 5\frac23, pretože 17:3 je 5 a zvyšok 2.
• \frac{15}{7}= 2\frac17, pretože 15:7 je 2 a zvyšok 1.