Slovenčina
Angličtina
Informatika
Vieme to
Nemčina
Biológia
Zemepis
Chémia
Fyzika
Aritmetika
Zlomky, percentá, desatinné čísla
Geometria
Elementárna algebra
Funkcie
Jednotky, miery
Diskrétna matematika
Finančná gramotnosť
Rozhodovačka
Pexeso
Krok za krokom
Počítanie
Grafár
Porozumenie
Označovanie
Presúvanie
Mriežkovaná
Rozdeľovačka
Pokazená kalkulačka
Roboti
Strieľačka
Príšerky
Preteky
Územia
Tipovačka
Tímovka
Môj účet
Odhlásiť saKružnica je množina všetkých bodov v rovine, ktoré majú od daného pevného bodu S rovnakú vzdialenosť r. Bod S nazývame stred kružnice, hodnotu r nazveme polomer kružnice.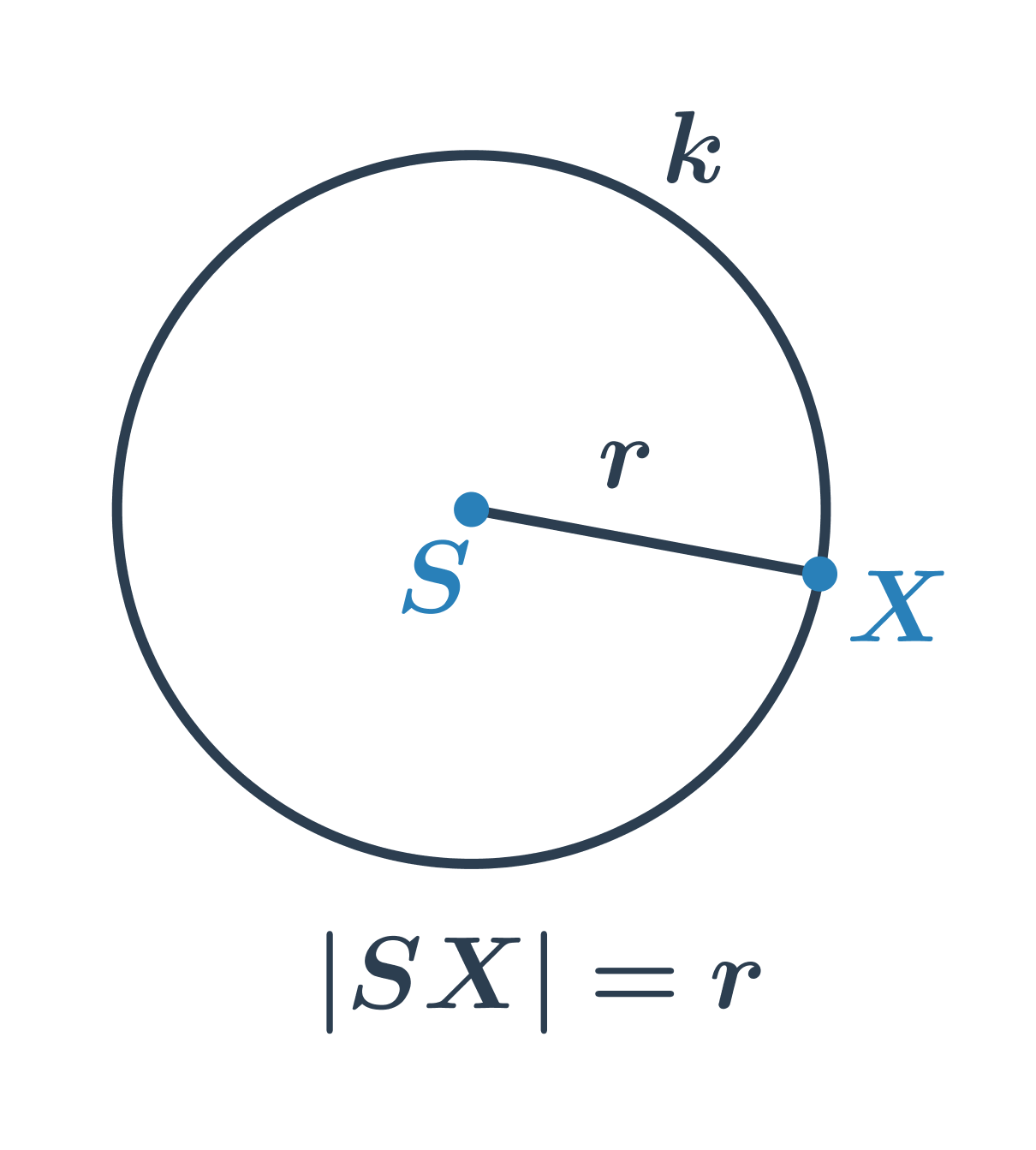 
Stredová rovnica kružnice
Stredová rovnica kružnice so stredom S[m;n] a polomerom r je v tvare: (x-m)^2 +(y-n)^2=r^2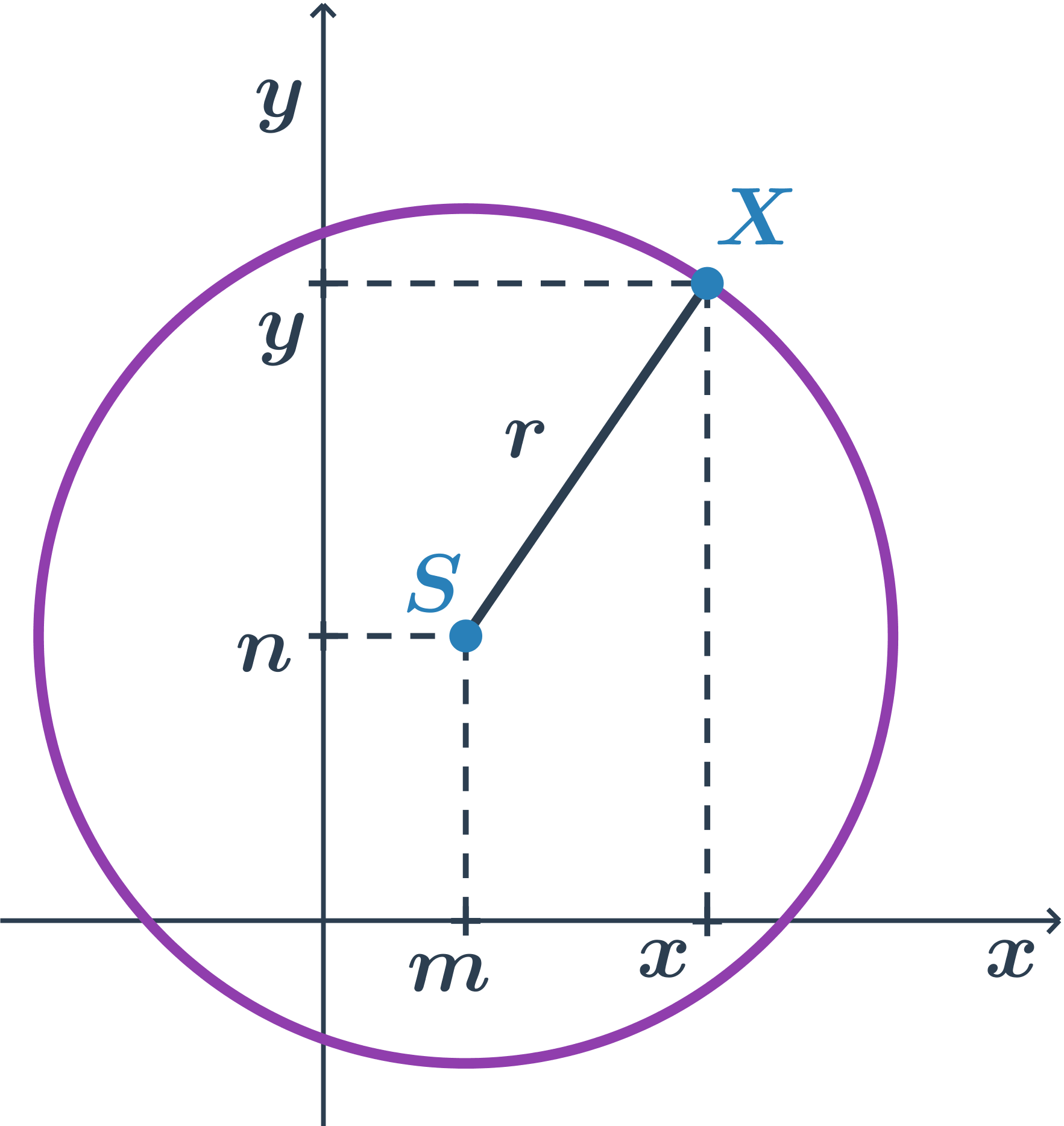 
Príklad: Určite stredovú rovnicu kružnice so stredom v bode S[-1;2] a polomerom r=3.
- Stredová rovnica je v tvare: (x-m)^2 +(y-n)^2=r^2
- Dosadíme súradnice stredu a polomer. Pri dosadení si dáme pozor na to, že súradnice stredu v stredovej rovnici odčítame: (x-(-1))^2 +(y-2)^2=3^2
- Po úprave: (x+1)^2 +(y-2)^2=9
Všeobecná rovnica kružnice
Podobne ako existuje niekoľko tvarov rovníc priamky, môžeme aj rovnicu kružnice zapísať rôznymi spôsobmi. Všeobecná rovnica kružnice je v tvare: x^2 +y^2-2mx-2ny+p=1.
Každá rovnica v tomto tvare ale nemusí ešte byť všeobecnou rovnicou kružnice. Pre všeobecnú rovnicu kružnice musí platiť, že výraz m^2+n^2-p je kladný. Praktické overenie, či ide o kružnicu, ale väčšinou vykonávame prevedením na stredovú rovnicu kružnice.
Príklad: Nájdite stred a polomer kružnice danej všeobecnou rovnicou x^2+y^2+4x+6y-12=0.
- Najskôr si usporiadame členy podľa premenných: x^2+4x+y^2-6y-12=0.
- Našim ďalším cieľom je upraviť výraz na ľavej strane ako súčet dvoch druhých mocnín (štvorcov), podľa vzorcov a^2\pm 2ab+b^2=(a\pm b)^2.
- K obom stranám rovnice pripočítame konštanty 4 a 9, aby sme súčty členov s premennými x a y mohli upraviť na druhé mocniny (prevedieme v oboch prípadoch doplnenie na štvorec): x^2+4x+4+y^2-6y+9-12=4+9
- A upravíme: (x+2)^2 +(y-3)^2-12=13
- Na záver ešte prevedieme -12 na druhú stranu rovnice: (x+2)^2 +(y-3)^2=25
- Týmto sme previedli všeobecnú rovnicu kružnice na stredovú rovnicu kružnice.
- Polomer kružnice je r=\sqrt{25}=5.
- Súradnice stredu S[m,n] odčítame v stredovej rovnici od premenných x a y, majú teda opačné znamienka než konštanty v zátvorkách v stredovej rovnici \Rightarrow S[-2;3].
Kružnica a priamka
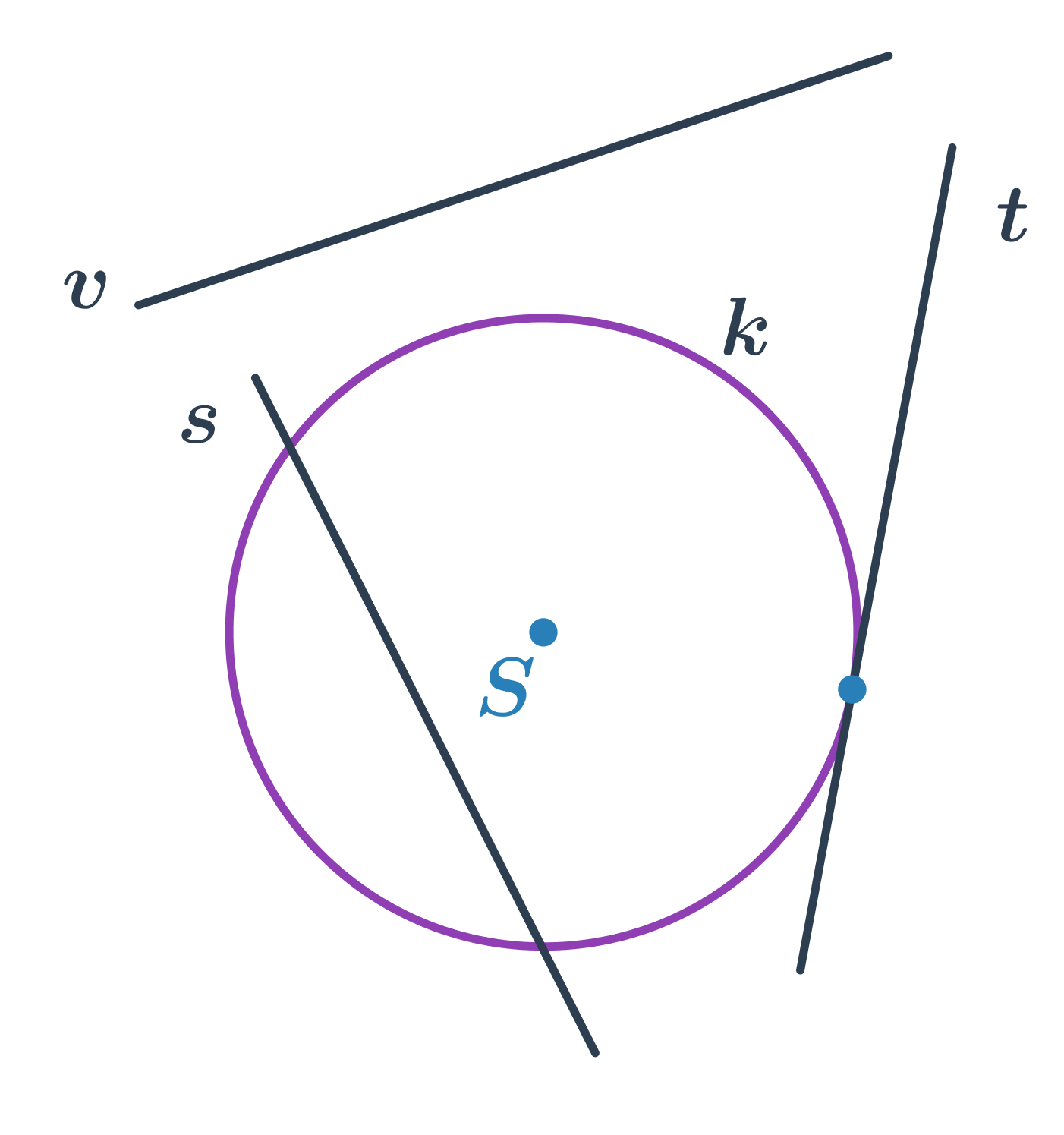
- priamka s pretína kružnicu v dvoch bodoch – sečnica kružnice
- priamka t pretína kružnicu v jednom bode – dotyčnica kružnice
- priamka v kružnici nepretína – vonkajšia priamka kružnice
Rovnice dotyčnice kružnice v bode, ktorý leží na kružnici
Kružnica daná rovnicou (x-m)^2 +(y-n)^2=r^2 má v bode T[x_0;y_0] dotyčnicu (x_0-m)(x-m) +(y_0-n)(y-n)=r^2.Ako si zapamätať rovnicu dotyčnice
- Stredová rovnica je v tvare (x-m)^2 +(y-n)^2=r^2.
- Zátvorky rozložíme na súčiny dvojčlenov (x-m)(x-m) +(y-n)(y-n)=r^2.
- V každom súčine zameníme jedno x za x_0 a jedno y za y_0
- Dostaneme rovnicu dotyčnice (x_0-m)(x-m) +(y_0-n)(y-n)=r^2
Príklad: Určite rovnicu dotyčnice kružnice (x-1)^2+(y+2)^2=13 v jej bode T[3;1].
- Overíme, či bod T leží na kružnici: (3-1)^2+(1+2)^2=13 \Rightarrow 4+9=13
- Dotyčnica má rovnicu (x_0-m)(x-m) +(y_0-n)(y-n)=r^2
- Dosadíme súradnice bodu T: (3-1)(x-1) +(1+2)(y+2)=13
- Roznásobíme zátvorky: 2x-2 +3y+6=13
- A dostaneme všeobecnú rovnicu dotyčnice 2x+3y-9=0
Polára kružnice
Z bodu R mimo kružnicu môžeme zostrojiť dve dotyčnice k danej kružnici. Priamka určená bodmi dotyku dotyčníc sa nazýva polára kružnice vzhľadom k bodu R.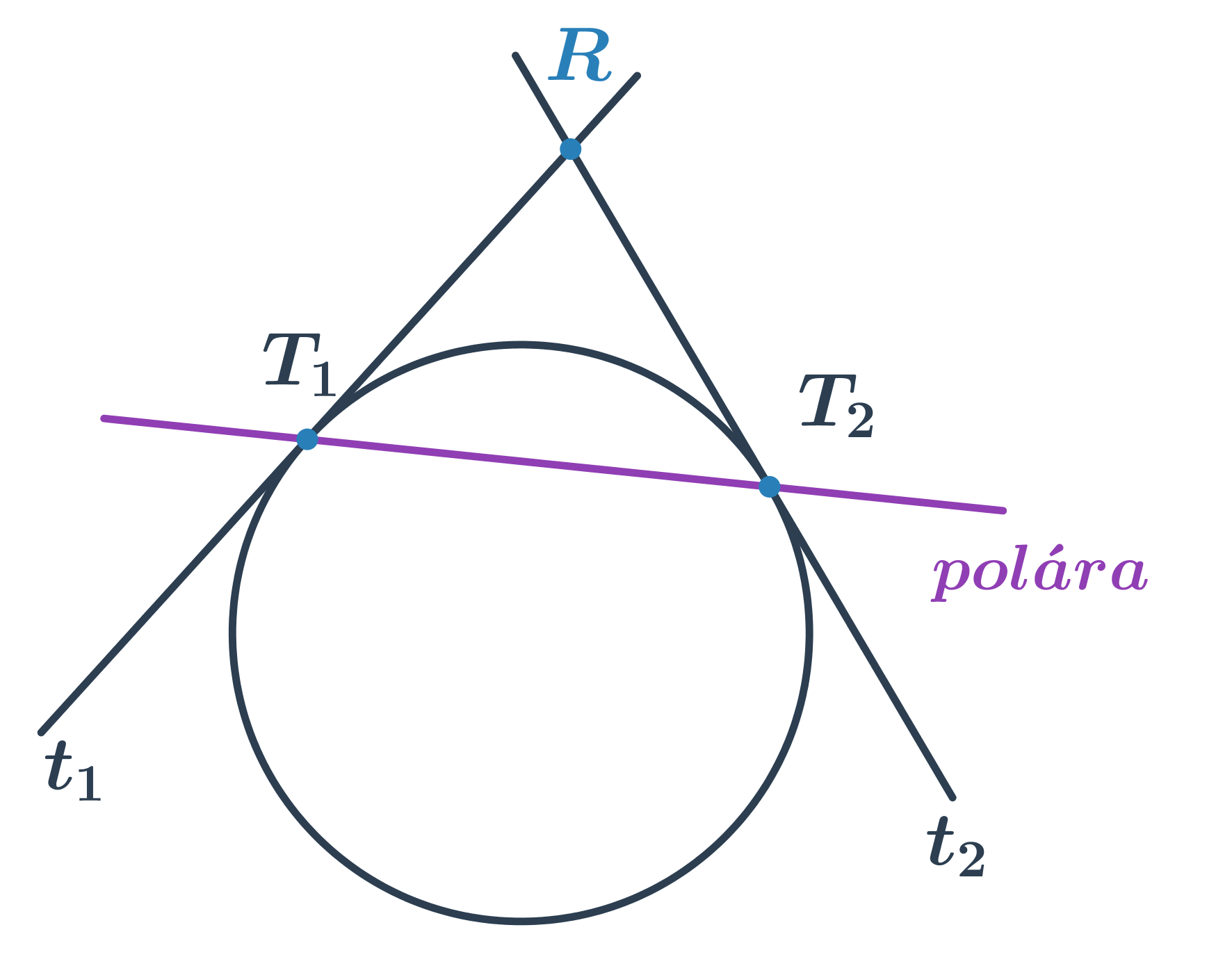 
Rovnica poláry kružnice (x-m)^2 +(y-n)^2=r^2 vzhľadom k bodu R[r_1;r_2] je (r_1-m)(x-m) +(r_2-n)(y-n)=r^2.
Na čo poláru použijeme?
- Poláru využívame na konštrukciu dotyčníc ležiacich z bodu mimo kružnicu.
- Podľa vzorca určíme rovnicu poláry, teda priamky.
- Nájdeme priesečníky poláry a kružnice – to sú body dotyku hľadaných dotyčníc.
- Keď poznáme body dotyku, určíme podľa vzťahu pre rovnicu dotyčnice v bode kružnice všeobecné rovnice oboch dotyčníc.
