Ďakujeme za vaše hodnotenie.

Lomené výrazy: úpravy a výpočty

GXJ

viemeto.eu/GXJ

Stiahnuť QR kód

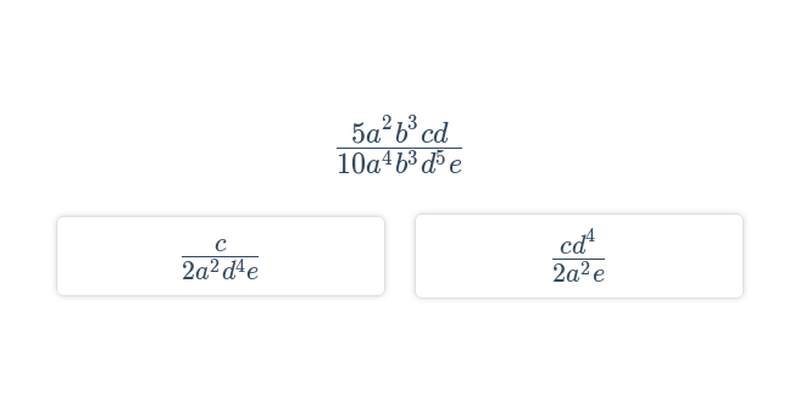
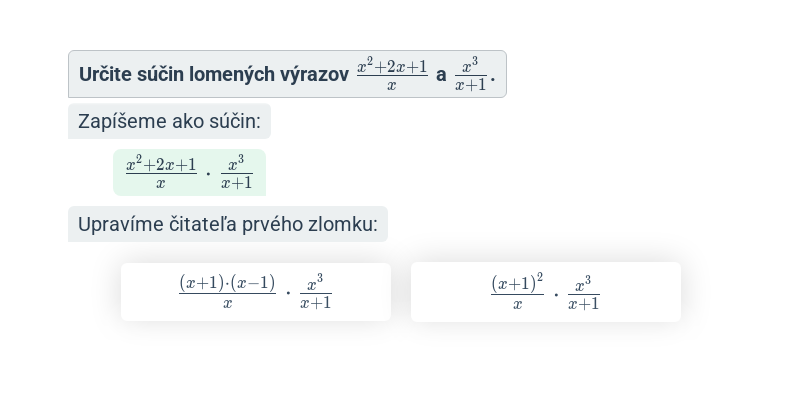
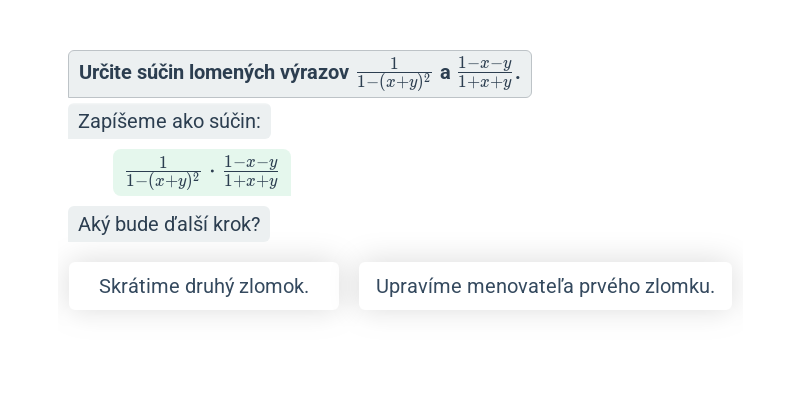
S lomenými výrazmi počítame podobne ako so zlomkami, iba musíme úpravy vykonávať s mnohočlenmi.

Príklad: úprava výrazu \frac{3}{4x} + \frac{2}{3x}

Prevedieme oba výrazy na spoločný menovateľ: \frac{9}{12x} + \frac{8}{12x}.
Sčítame: \frac{9+8}{12x} = \frac{17}{12x}.

Príklad: úprava výrazu \frac{x+y}{x^2-y^2}

Menovateľ rozpíšeme pomocou vzorca x^2-y^2=(x+y)(x-y).
Dostávame \frac{x+y}{(x+y)(x-y)}.
Pokrátime na \frac{1}{x-y}.

Rozhodovačka

Rýchle precvičovanie výberom z dvoch možností.

Lomené výrazy: úpravy a výpočty

Úpravy lomených výrazov

Rozhodovačka • ťažké

Krok za krokom

Doplňovanie jednotlivých krokov v rozsiahlejšom postupe.

Lomené výrazy: úpravy a výpočty

Počtové operácie s lomenými výrazmi

Krok za krokom • stredné

Počítanie

Cvičenie, v ktorom píšete odpoveď na klávesnici.

Lomené výrazy: úpravy a výpočty

Počítanie • stredné

Predchádzajúce

Nadväzujúce

Cvičenie

Lomené výrazy: úpravy a výpočty

viemeto.eu/GXJ

Rozhodovačka

Úpravy lomených výrazov

Krok za krokom

Počtové operácie s lomenými výrazmi

Počítanie