Slovenčina
Angličtina
Informatika
Vieme to
Nemčina
Biológia
Zemepis
Chémia
Fyzika
Aritmetika
Zlomky, percentá, desatinné čísla
Geometria
Elementárna algebra
Funkcie
Jednotky, miery
Diskrétna matematika
Finančná gramotnosť
Rozhodovačka
Pexeso
Krok za krokom
Počítanie
Grafár
Porozumenie
Označovanie
Presúvanie
Mriežkovaná
Rozdeľovačka
Pokazená kalkulačka
Roboti
Strieľačka
Príšerky
Preteky
Územia
Tipovačka
Tímovka
Môj účet
Odhlásiť saVýpis prehľadov
Úsečky
Prechádzate súhrny informácií k určitým témam. Systémy Vieme sa zameriavajú hlavne na ich precvičovanie. K cvičeniam k jednotlivým podtémam sa dostanete pomocou odkazov nižšie.
Podkapitoly
Úsečka je časť priamky medzi dvomi krajnými bodmi (vrátane týchto bodov). Úsečka je v rovine aj v priestore jednoznačne zadaná svojimi krajnými bodmi.
HoreDĺžka úsečky v rovine
Dĺžku úsečky v rovine vypočítame rovnako ako vzdialenosť bodov v rovine.
Ak sú dané súradnice A[x_A; y_A], B[x_B; y_B], je dĺžka úsečky AB:
|AB| = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2}
Vzorec vychádza z Pytagorovej vety.
Je nutné počítať rozdiel súradníc v poradí „druhý bod mínus prvý“?
- Nie je. Výrazy x_B-x_A a x_A-x_B nie sú rovnaké. Ale sú opačné a vo vzorci počítame ich druhé mocniny, ktoré sa rovnajú.
- Naviac geometricky je dĺžka úsečky AB rovnaká ako dĺžka úsečky BA.
- Dôvodom zápisu práve v tomto tvare je fakt, že dĺžka úsečky je rovná veľkosti vektora \overrightarrow{AB} a pri vektore sa jeho veľkosť vždy počíta „koncový bod mínus počiatočný“.
Príklad: Dĺžka úsečky EF: E[0;-1], F[-4;2]
- |EF| = \sqrt{(x_F-x_E)^2 + (y_F-y_E)^2}
- Dosadíme súradnice bodov E[0;-1] a F[-4;2]: \sqrt{(-4-0)^2 + (2-(-1))^2}=\sqrt{4^2 + 3^2}=\sqrt{25}=5
- Dĺžka úsečky je: |EF|=5
Stred úsečky v rovine
Stred úsečky delí úsečku na dve rovnaké časti. Ak ležia krajné body úsečky AB na číselnej osi a ich polohám zodpovedajú hodnoty a a b, potom jej stredu S zodpovedá číslo s=\frac{a+b}{2}. Stred úsečky je „priemerom“ jej krajných bodov.
Pre úsečku v rovine bude situácia nasledujúca.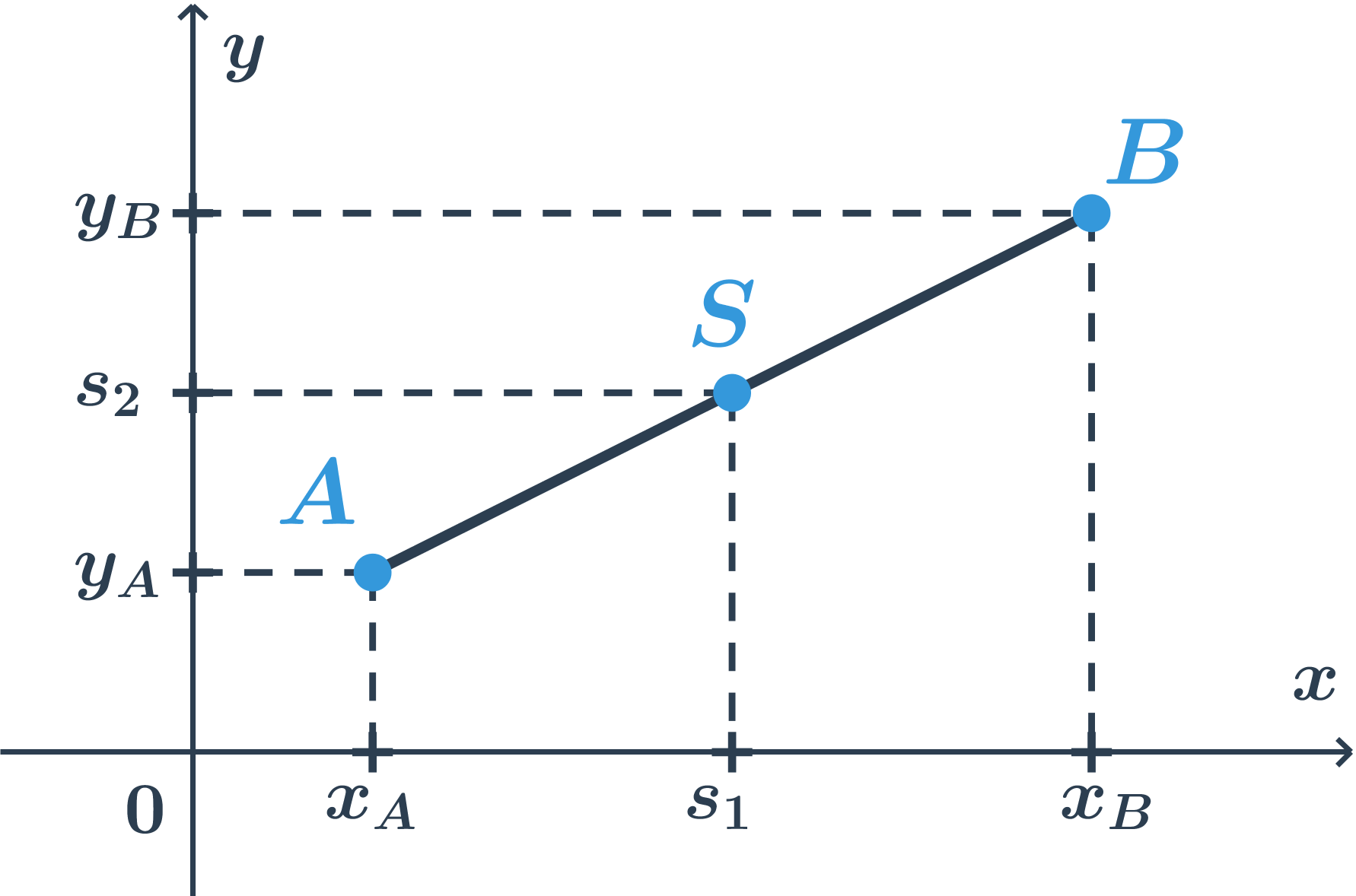 
Situácia na oboch súradných osách je rovnaká ako predtým. Vypočítame obe súradnice stredu ako priemery zodpovedajúcich súradníc krajných bodov.
Pre stred S[s_1;s_2] úsečky AB, kde A[x_A; y_A], B[x_B; y_B] platí:
s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
Príklad: určenie stredu úsečky
Nájdite stred úsečky AB: A[6;-1], B[2;3]
- Pre súradnice stredu S[s_1;s_2] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
- Dosadíme súradnice bodov A[6;-1], B[2;3]: s_1 = \frac{6+2}{2}=4, s_2 = \frac{-1+3}{2}=1
- Stred úsečky AB je bod S[4;1]
Príklad: určenie druhého krajného bodu úsečky
Určite súradnice druhého krajného bodu úsečky AB, ak je daný bod A[-3;0] a jej stred S[1;3].
- Pre súradnice stredu S[s_1;s_2] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
- Dosadíme súradnice bodov A[-3;0], S[1;3]: 1 = \frac{-3+x_B}{2}, 3 = \frac{0+y_B}{2}
- Dopočítame neznáme x_B, y_B: 2=-3+x_B\Rightarrow x_B=5\\ 6=0+y_B\Rightarrow y_B=6
- Bod B má súradnice [5;6].
Vzájomná poloha úsečiek v rovine
Dve úsečky v rovine môžu mať spoločné krajné body, potom hovoríme, že sú totožné. Ak sa úsečky pretínajú v jednom bode, hovoríme, že sú rôznobežné. Úsečky sa tiež nemusia pretínať, nemajú teda žiadny spoločný bod. Špeciálne môžu v tomto prípade byť rovnobežné.
HoreDĺžka úsečky v priestore
Dĺžku úsečky v priestore vypočítame rovnako ako vzdialenosť bodov v priestore.
Ak sú dané súradnice A[x_A; y_A;z_A], B[x_B; y_B;z_B], je dĺžka úsečky AB:
|AB| = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2+(z_B-z_A)^2}
Príklad: Dĺžka úsečky EF: E[-2;0;1], F[-4;2;0]
- |EF| = \sqrt{(x_F-x_E)^2 + (y_F-y_E)^2+ (z_F-z_E)^2}
- Dosadíme súradnice bodov EF; E[-2;0;1], F[-4;2;0]:
\sqrt{(-4-(-2))^2 + (2-0)^2+(0-1)^2}=\sqrt{(-2)^2 + 2^2+(-1)^2}=\sqrt{4+4+1}=\sqrt{9}=3 - Dĺžka úsečky je: |EF|=3
Stred úsečky v priestore
Stred úsečky v priestore vypočítame podobne ako stred úsečky v rovine. Vypočítame všetky súradnice stredu ako priemery zodpovedajúcich súradníc krajných bodov.
Pre stred S[s_1;s_2;s_3] úsečky AB, kde A[x_A; y_A;z_A], B[x_B; y_B;z_B] platí:
s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2} , s_3 = \frac{z_A+z_B}{2}
Príklad: určenie stredu úsečky
Nájdite stred úsečky AB: A[2;1;-3], B[2;-3;3]
Pre súradnice stredu S[s_1;s_2;s_3] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}, s_3 = \frac{z_A+z_B}{2}
- Dosadíme súradnice bodov A[2;1;-3], B[2;-3;3].
- s_1 = \frac{2+2}{2}=2, s_2 = \frac{1-3}{2}=-1, s_3 = \frac{-3+3}{2}=0
Stred úsečky AB je bod S[2;-1;0]
Príklad: určenie druhého krajného bodu úsečky
Určite súradnice druhého krajného bodu úsečky AB, ak je daný bod A[1;2;4] a jej stred S[1;-3;0].
- Pre súradnice stredu S[s_1;s_2;s_3] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}, s_3 = \frac{z_A+z_B}{2}
- Dosadíme súradnice bodov A[1;2;4], S[1;-3;0].
- 1 = \frac{1+x_B}{2}, -3 = \frac{2+y_B}{2}, 0 = \frac{4+z_B}{2}
- Dopočítame neznáme x_B, y_B, z_B:
\begin{array}{rclcrcr} 2&=&1+x_B &\Rightarrow& x_B&=&1\\ -6&=&2+y_B &\Rightarrow& y_B&=&-8\\ 0&=&4+z_B&\Rightarrow& z_B&=&-4 \end{array}
- Bod B má súradnice [2;-8;-4].
Vzájomná poloha úsečiek v priestore
Podobne ako v rovine môžu mať dve úsečky spoločné krajné body, potom hovoríme, že sú totožné. Ak sa úsečky pretínajú v jednom bode, hovoríme, že sú rôznobežné. Úsečky sa tiež nemusia pretínať, nemajú teda žiadny spoločný bod. Špeciálne môžu v tomto prípade byť rovnobežné.
Hore
