Výpis prehľadov
Zlomky
Prechádzate súhrny informácií k určitým témam. Systémy Vieme sa zameriavajú hlavne na ich precvičovanie. K cvičeniam k jednotlivým podtémam sa dostanete pomocou odkazov nižšie.
Podkapitoly
Zlomky zapisujeme v tvare \frac{a}{b}, kde a sa nazýva čitateľ a b menovateľ. Aby mal zlomok zmysel, nesmie byť menovateľ nula. Význam zlomku zodpovedá deleniu. Napríklad: v zlomku \frac32 je čitateľom číslo 3 a menovateľom číslo 2, hodnota zlomku \frac32 sa rovná deleniu 3:2 = 1{,}5 („jeden a pol“).
Rozširovanie a krátenie
Hodnota zlomku sa nemení rozširovaním a krátením (nenulovým číslom c).
| Rozšírenie číslom c: | \frac{a}{b} = \frac{c\cdot a}{c \cdot b} |
| Krátenie číslom c: | \frac{a}{b} = \frac{a:c}{b:c} |
Príklady:
- Rozšírenie zlomku \frac64 číslom 5: \frac64 = \frac{6\cdot 5}{4\cdot 5} = \frac{30}{20}.
- Krátenie zlomku \frac64 číslom 2: \frac64 = \frac{6:2}{4:2} = \frac{3}{2}.
Základný tvar
Vďaka rozširovaniu a kráteniu môžeme rovnakú hodnotu zapísať nekonečným množstvom rôznych zlomkov. Zlomok \frac{a}{b} je v základnom tvare, ak sú čísla a, b nesúdeliteľné (ich jediný kladný spoločný deliteľ je teda číslo 1). Príklady:
- Zlomok \frac64 nie je v základnom tvare, pretože čísla 6 a 4 sú súdeliteľné (majú spoločný deliteľ 2, ktorým je možné zlomok krátiť).
- Zlomok \frac34 je v základnom tvare, pretože čísla 3 a 4 sú nesúdeliteľné.
Zlomky: základy
Zlomky zapisujeme v tvare \frac{a}{b}, kde a sa nazýva čitateľ a b menovateľ. Aby mal zlomok zmysel, nesmie byť menovateľ nula. Význam zlomku zodpovedá deleniu. Príklad: v zlomku \frac32 je čitateľom číslo 3 a menovateľom číslo 2, hodnota zlomku \frac32 sa rovná deleniu 3:2 = 1{,}5 („jedna a pol“).
Zlomok \frac{a}{b} je v základnom tvare, ak sú čísla a, b nesúdeliteľné (teda ich jediný kladný spoločný deliteľ je číslo 1). Na základný tvar prevádzame zlomky pomocou krátenia. Príklady:
- Zlomok \frac64 nie je v základnom tvare, pretože čísla 6 a 4 sú súdeliteľné – majú spoločný deliteľ 2, ktorým je možné zlomok krátiť, čím dostávame základný tvar \frac32.
- Zlomok \frac34 je v základnom tvare, pretože čísla 3 a 4 sú nesúdeliteľné.
Základy práce so zlomkami si môžete precvičiť v týchto témach:
HoreUrčovanie zlomkov
Zlomky vyjadrujú „časti z celku“. Môžeme ich graficky vyjadriť mnohými spôsobmi:

Zlomky na číselnej osi
Zlomok môžeme na číselnú os umiestniť tak, že ho prevedieme na desatinné číslo (vydelíme jednoducho čitateľ menovateľom) a potom postupujeme rovnako ako pri desatinných číslach. Napríklad \frac{6}{5} = 1{,}2, teda zlomok \frac{6}{5} leží dve desatiny za jednotkou. Ďalšie príklady:
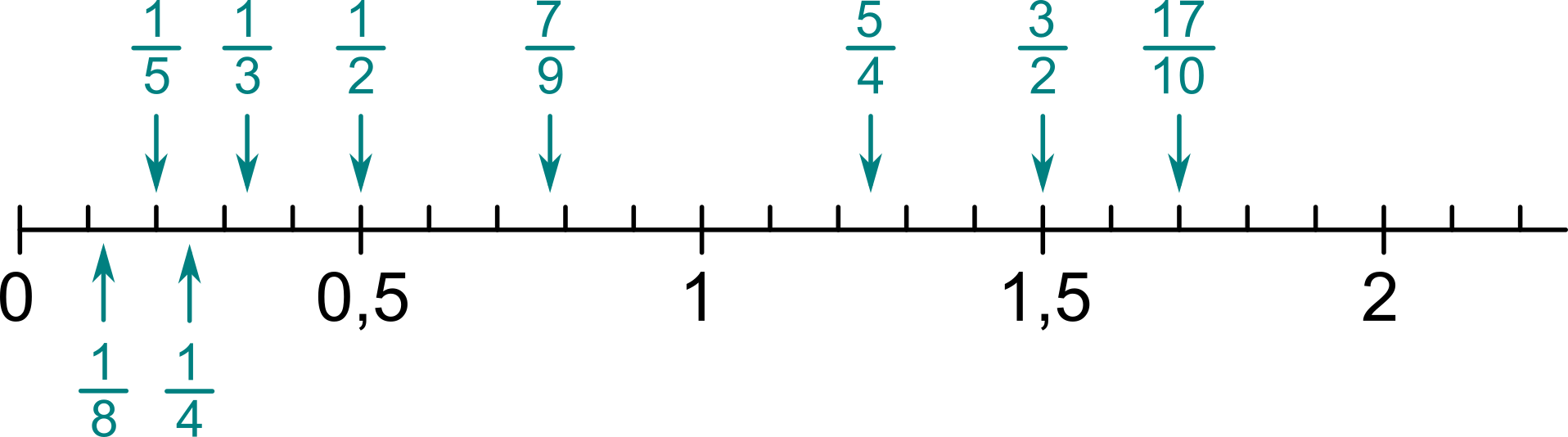
Zlomky menšie než 1 môžeme umiestňovať na číselnú os tiež priamo (bez prevodu na desatinné číslo) vďaka predstave „časť z celku“. Ak máme umiestniť zlomok \frac{3}{7}, predstavíme si, ako by sme rozdelili úsečku od 0 po 1 na sedem rovnakých častí. Zlomok \frac{3}{7} potom umiestnime na tretiu pozíciu.
Hodí sa si vybudovať dobrú predstavu hlavne pre zlomky s malým menovateľom:
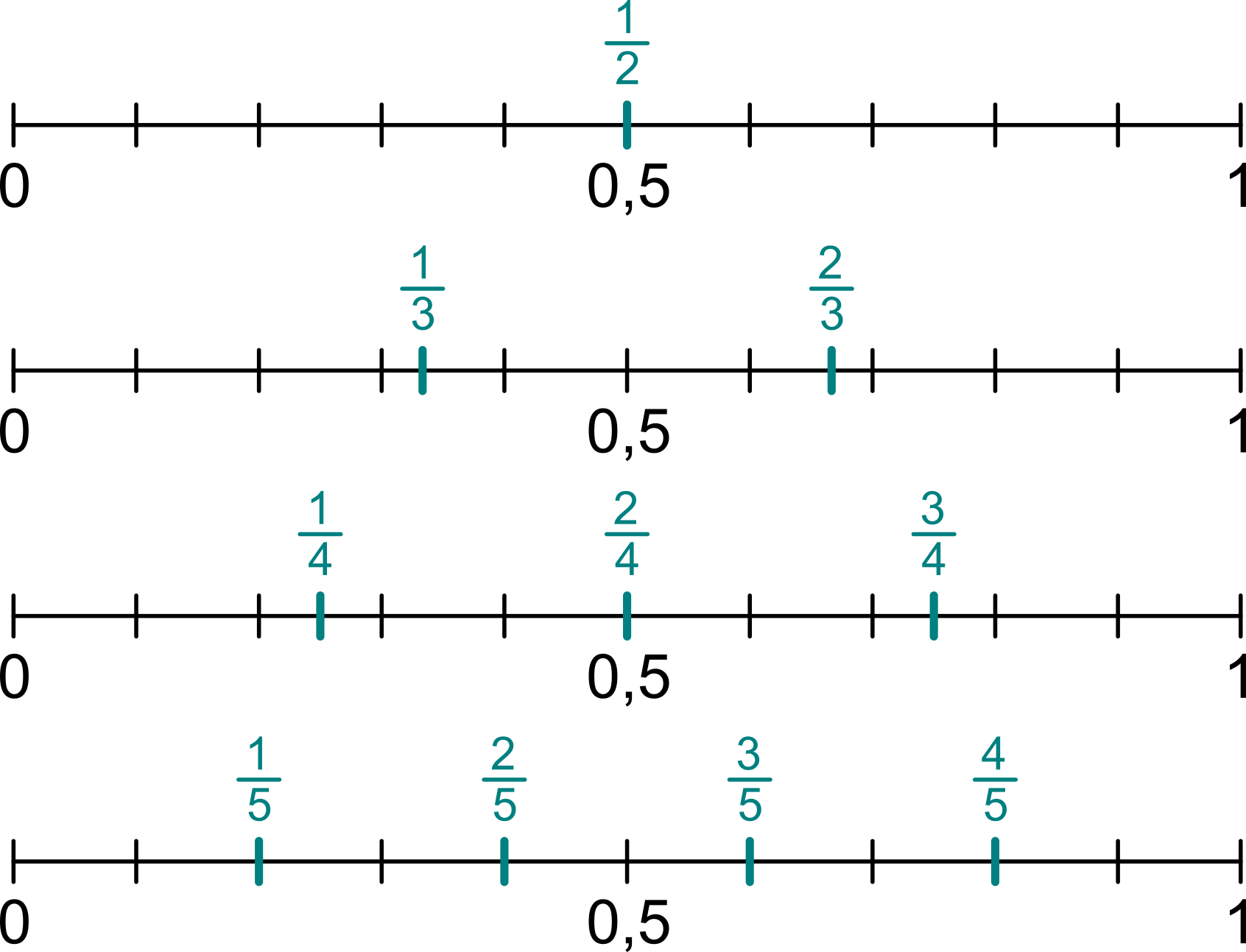
Porovnávanie zlomkov
Než sa pustíme do porovnávania zlomkov, je dobré mať jasno v tom, čo je čitateľ („to hore“) a menovateľ („to dole“). V zlomku \frac{3}{7} je 3 čitateľ, 7 menovateľ.
Porovnávanie zlomkov s rovnakým menovateľom
Porovnávania zlomkov s rovnakým menovateľom je jednoduché: stačí jednoducho porovnať čitatele. Ak napríklad porovnávame zlomky \frac{3}{7} a \frac{5}{7}, je väčší druhý zlomok. Oba zlomky vyjadrujú sedminy z celku a je jednoducho viac, keď máme sedmín päť.
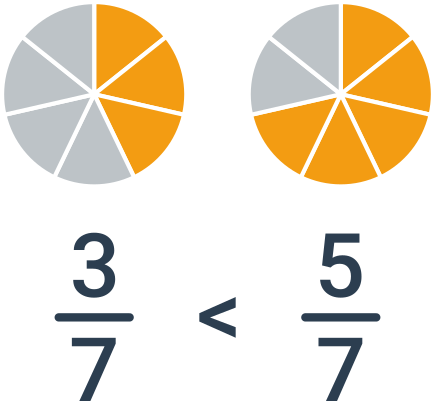
Porovnávanie zlomkov s rovnakým čitateľom
Ak majú zlomky rovnaký čitateľ, potom stačí porovnať menovatele. V tomto prípade je ale poradie zlomkov opačné než poradie menovateľov. Ak porovnávame napríklad zlomky \frac{1}{4} a \frac{1}{5}, je väčšia jedna štvrtina: dostanem väčší kúsok pizzy, ak sa bude deliť medzi 4 ľudí, než keď sa bude deliť medzi 5 ľudí.
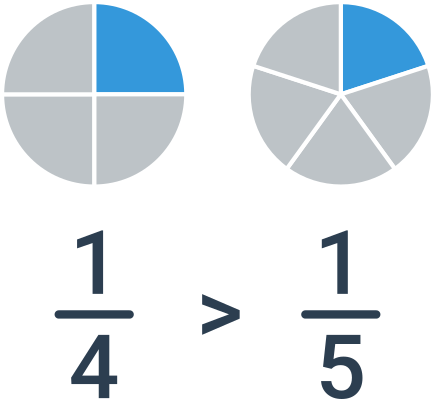
Odlišný menovateľ aj čitateľ
V tomto prípade potrebujeme zlomky najskôr previesť na spoločný menovateľ a až potom vykonať porovnanie podľa čitateľov. Príklad: porovnanie zlomkov \frac{2}{3} a \frac{4}{7}. Najmenší spoločný menovateľ je 21, po rozšírení dostávame dvojicu zlomkov \frac{2}{3}=\frac{2\cdot 7}{3\cdot 7}=\frac{14}{21} a \frac{4}{7}=\frac{4\cdot 3}{7\cdot 3}=\frac{12}{21}. Pretože 14 > 12, je väčší prvý zlomok, tj. \frac{2}{3}.
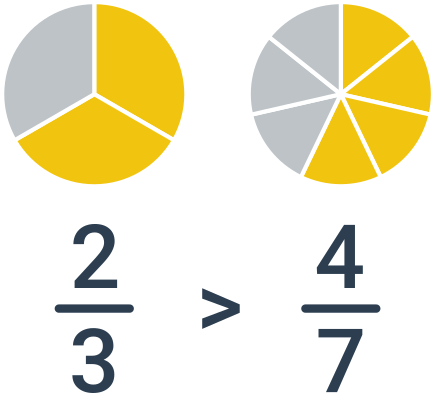
Porovnanie bez výpočtu
Často môžeme vykonať porovnanie aj bez detailného výpočtu, ak si zlomky správne predstavíme alebo porovnáme s vhodnou hodnotou „medzi“:
Zlomky \frac{2}{3} a \frac{7}{6}. Prvý z nich je menší než 1, druhý je väčší než 1. Platí teda \frac{2}{3} < \frac{7}{6}.
Zlomky \frac{1}{3} a \frac{4}{5}. Prvý z nich je určite menší než polovica, druhý je výrazne väčší než polovica. Platí teda \frac{1}{3} < \frac{4}{5}.
Zmiešané čísla
Ak má zlomok menovateľ väčší než čitateľ (zlomok je menší než jedna), označuje sa zlomok ako pravý. Nepravé zlomky (teda tie, ktoré sú väčšie ako jedna) môžeme zapísať pomocou zmiešaného čísla. Zmiešané číslo a\frac{b}{c} je zápis súčtu a + \frac{b}{c}, kde \frac{b}{c} je kladný zlomok menší než jedna. Príklady:
- 1\frac{1}{2} = \frac{3}{2}
- 2\frac{3}{5} = \frac{13}{5}
Prevod zmiešaného čísla na zlomok urobíme na základe pozorovania, že jednotku môžeme zapísať ako \frac{c}{c}. Príklad: 3\frac14 = 3\cdot\frac44 + \frac14 = \frac{12}{4}+\frac14 = \frac{13}{4}.

Prevod nepravého zlomku na zmiešané číslo urobíme pomocou delenia so zvyškom. Celá časť zmiešaného čísla zodpovedá podielu, čitateľ zvyšného zlomku zodpovedá zvyšku. Príklad:
- \frac{17}{3} = 5\frac23, pretože 17:3 je 5 a zvyšok 2.
- \frac{15}{7}= 2\frac17, pretože 15:7 je 2 a zvyšok 1.
Výpočty so zlomkami
Základné výpočty so zlomkami sú nasledujúce:
- Zlomky sa krátia tak, že čitateľ aj menovateľ vydelíme ich spoločným deliteľom.
- Zlomok \frac{9}{12} môžeme skrátiť na \frac{3}{4}, pretože čitateľ aj menovateľ majú spoločný deliteľ 3.
- Pre sčítanie a odčítanie zlomkov je nutné previesť zlomky na spoločný menovateľ.
- \frac{1}{4} + \frac{1}{6} prevedieme na spoločný menovateľ 12 a dostaneme \frac{3}{12} + \frac{2}{12} = \frac{5}{12}.
- Násobenie sa vykonáva tak, že vynásobíme čitateľ aj menovateľ medzi sebou.
- \frac{2}{3} \cdot \frac{3}{4} = \frac{6}{12} = \frac{1}{2}
- Delenie sa vykonáva násobením prevráteného zlomku.
- \frac{2}{3} : \frac{3}{4} = \frac{2}{3} \cdot \frac{4}{3} = \frac{8}{9}
- Prevod zlomku na percentá sa vykonáva pomocou násobenia 100.
- \frac{3}{4} = 0{,}75 = 75 \%
- Zlomky prevedieme na desatinné čísla tak, že čitateľ vydelíme menovateľom. Naopak desatinné číslo je možné previesť na zlomok pomocou roznásobenie mocninami desiatky.
- \frac{2}{5} = 2 : 5 = 0{,}4
- 0{,}25 = 0{,}25 \cdot\frac{100}{100} = \frac{25}{100}, čo po skrátení dáva \frac{1}{4}
Kombinácie operácií so zlomkami
- Zadania kombinujúce rôzne aritmetické operácie so zlomkami.
Krátenie zlomkov
Rovnakú hodnotu môžeme vyjadriť mnohými zlomkami, napríklad \frac23 = \frac46 = \frac{10}{15} = \frac{200}{300}. Len jedno možné vyjadrenie však považujeme za základný tvar. Zlomok je v základnom tvare, ak sú čitateľ a menovateľ nesúdeliteľné, nemajú teda žiadny spoločný deliteľ okrem jednotky. V uvedenom príklade je v základnom tvare zlomok \frac23.
Ako krátenie zlomku sa označuje operácia, kedy čitateľ a menovateľ vydelíme rovnakým, nenulovým číslom. Krátenie zachováva hodnotu zlomku. Ak chceme zlomok previesť do základného tvaru, krátime najväčším spoločným deliteľom čitateľa a menovateľa.
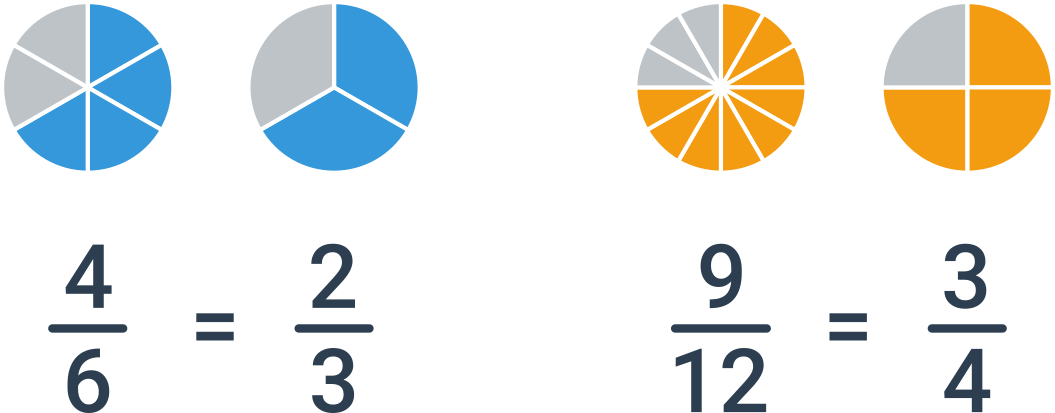
Príklady
Zlomok \frac{15}{28} je v základnom tvare, pretože čísla 15 a 28 nemajú spoločný deliteľ (sú nesúdeliteľné).
Zlomok \frac{25}{30} môžeme krátiť číslom 5, čím dostaneme zlomok \frac{5}{6}, ktorý je v základnom tvare.
Zlomok \frac{12}{18} môžeme krátiť číslom 2, čím dostaneme zlomok \frac{6}{9}. Ak chceme krátiť na základný tvar, nájdeme najväčší spoločný deliteľ čísel 12 a 18, čo je 6. Po krátení číslom 6 dostávame zlomok \frac{2}{3}.
Sčítanie a odčítanie zlomkov
Než sa pustíme do sčítania zlomkov, je dobré mať jasno v tom, čo je čitateľ („to hore“) a menovateľ („to dole“). V zlomku \frac{3}{7} je 3 čitateľ, 7 menovateľ.
Sčítanie zlomkov s rovnakým menovateľom
Ak majú sčítané zlomky rovnaké menovatele, stačí jednoducho sčítať čitatele. Menovateľ necháme rovnaký, teda \frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}.
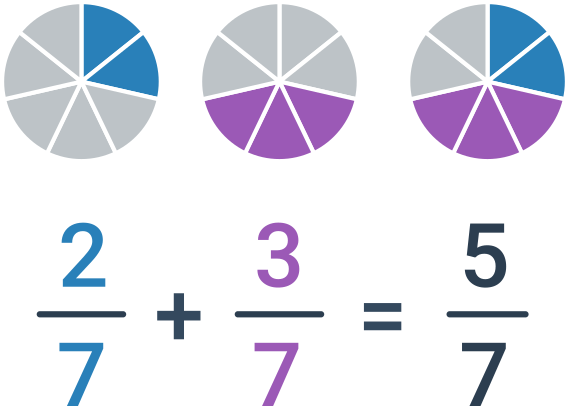
Sčítanie zlomkov s rôznymi menovateľmi
Ak majú sčítané zlomky rôzne menovatele, musíme ich najskôr rozšíriť tak, aby mali rovnaký menovateľ. Najvýhodnejšie je rozšíriť zlomky na najmenší spoločný násobok pôvodných menovateľov. Keď už majú zlomky rovnaký menovateľ, sčítame ich vyššie uvedeným postupom.
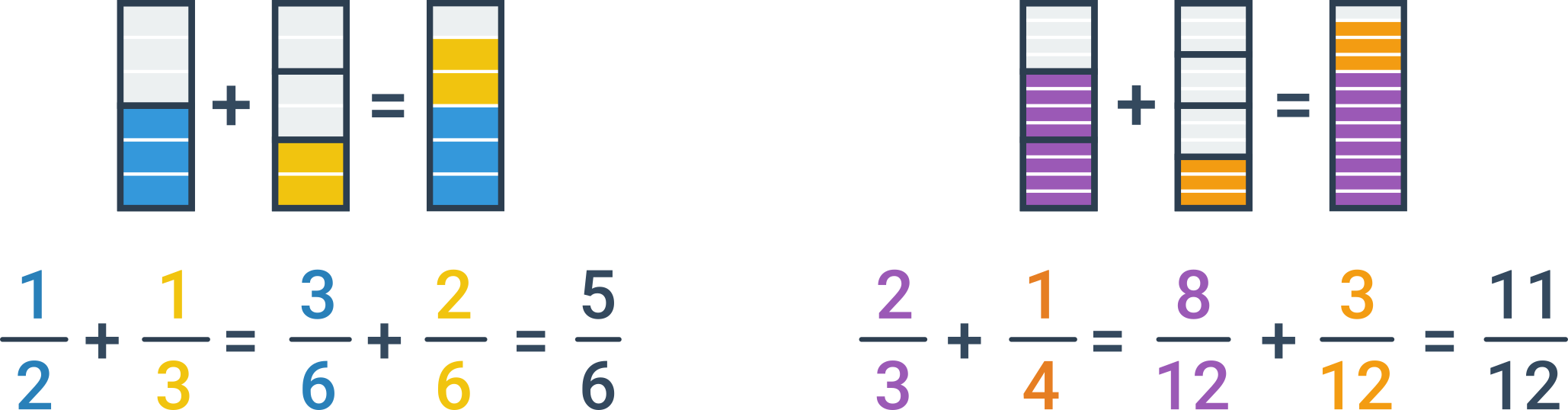
Úpravy a odčítanie
Výsledný zlomok väčšinou ešte krátime, aby sme dostali výsledok v základnom tvare. Odčítanie zlomkov funguje rovnakým spôsobom.
Príklady
Príklad s rovnakým menovateľom, bez nutnosti krátenia:
\frac{2}{5}+\frac{1}{5} = \frac{2+1}{5} = \frac{3}{5}.Príklad s rovnakým menovateľom, kedy výsledok krátime:
\frac{5}{6}-\frac{1}{6} = \frac{5-1}{6} = \frac{4}{6} = \frac{2}{3}.Príklad s rôznymi menovateľmi: \frac{5}{6} - \frac{3}{4}. Najmenší spoločný násobok menovateľov 6 a 4 je 12, rozšírime teda zlomky na menovateľ 12:
\frac{5}{6} - \frac{3}{4} = \frac{5\cdot 2}{6\cdot 2} - \frac{3\cdot 3}{4\cdot 3}= \frac{10}{12} - \frac{9}{12} = \frac{1}{12}
Násobenie a delenie zlomkov
Násobenie zlomkov si môžeme predstaviť s pomocou čokolády. Ak násobíme \frac45\cdot \frac23 je to ako keby sme brali štyri z piatich stĺpčekov a dva z troch riadkov. Koľko štvorčekov čokolády takto vezmeme? Osem z pätnástich, teda \frac{8}{15}.

Pri násobení zlomkov teda jednoducho vynásobíme čitateľ prvého zlomku a čitateľ druhého zlomku a dostaneme výsledný čitateľ, podobne pre menovateľ: \frac{a}{b}\cdot \frac{c}{d} = \frac{a\cdot c}{b\cdot d}. Ak sa chceme vyhnúť násobeniu veľkých čísel, môžeme zlomky krátiť, a to aj „do kríža“. Príklady:
- \frac{2}{3}\cdot\frac{1}{5} = \frac{2\cdot 1}{3\cdot 5}=\frac{2}{15}
- \frac{2}{3}\cdot\frac{3}{4} = \frac{2\cdot 3}{3\cdot 4}=\frac{2}{4}=\frac{1}{2} (všimnite si, že neroznásobujeme, ale hneď krátime)
Delenie zlomkov je to isté ako násobenie prevráteným zlomkom: \frac{a}{b}:\frac{c}{d} = \frac{a}{b}\cdot\frac{d}{c}=\frac{a\cdot d}{b\cdot c}. Príklady:
- \frac13:\frac12 =\frac13\cdot \frac21 = \frac23
- \frac{2}{5}:\frac{3}{4}=\frac{2}{5}\cdot \frac{4}{3} = \frac{2\cdot 4}{5\cdot 3} = \frac{8}{15}
Zlomky, mocniny, odmocniny
Umocňovanie a odmocňovanie zlomkov
Pri umocňovaní (odmocňovaní) zlomku jednoducho umocníme (odmocníme) čitateľ aj menovateľ:
\large(\frac{2}{3}\large)^2 = \frac{2^2}{3^2} = \frac{4}{9}
\sqrt{\frac{2}{3}} = \frac{\sqrt{2}}{\sqrt{3}}
\large(\frac{4}{5}\large)^{-1} = \frac{4^{-1}}{5^{-1}} = \frac{5}{4} (umocňovanie na -1 zodpovedá zameneniu čitateľa a menovateľa)
Umocňovanie na zlomok
Umocňovanie na zlomok zodpovedá tomu, že vezmeme mocninu podľa čitateľa a odmocninu podľa menovateľa, teda x^\frac{a}{b} = \sqrt[b]{a^x}. Príklady:
2^\frac{2}{3} = \sqrt[3]{2^2} = \sqrt[3]{4} = 1{,}587\ldots
4^\frac{1}{2} = \sqrt{4^1} = 2
81^\frac{3}{4} = \sqrt[4]{81^3} = \sqrt[4]{81}^3 = 3^3 = 27

