Výpis prehľadov
Geometrické konštrukcie
Prechádzate súhrny informácií k určitým témam. Systémy Vieme sa zameriavajú hlavne na ich precvičovanie. K cvičeniam k jednotlivým podtémam sa dostanete pomocou odkazov nižšie.
Podkapitoly
Geometrické konštrukcie
Ako konštrukčnú úlohu chápeme takú, v ktorej chceme zostrojiť určitý geometrický útvar (aspoň jeden, prípadne všetky) spĺňajúci dané podmienky. Inými slovami, pomocou pravítka, kružidla a prípadne aj uhlomeru zostrojíme geometrický útvar (trojuholník, obdĺžnik atď.), pre ktorý poznáme dĺžky jeho strán, veľkosti uhlov či iné vlastnosti.
Pred rysovaním je dobré si ujasniť:
- body značíme veľkými písmenami, napr. bod A
- priamky značíme malými písmenami, napr. priamka p
Riešenie konštrukčnej úlohy sa väčšinou skladá z niekoľkých krokov.
Náčrtok: Od ruky si nakreslíme obrázok hľadaného útvaru so všetkým, čo poznáme zo zadania. To nám pomôže predstaviť si výsledok. V rámci prehľadnosti si môžeme jednotlivé prvky vyznačiť farebne. Nezabudnite, náčrtky robíme veľké a prehľadné, aby sme v nich všetko pekne videli.
Popis konštrukcie: Popis jednotlivých krokov, ktoré musíme urobiť, aby sme dospeli k výsledku. Popis píšeme preto, aby každý mohol náš postup zopakovať. Z výsledného obrázku to nie je vždy ľahko možné. Pre zápis konštrukcie používame geometrické značenie. Popis konštrukcie väčšinou riešime až vo vyšších ročníkoch.
Konštrukcia: Je rysovanie príkladu.
Skúška správnosti: Mali by sme si overiť, či obrázok skutočne spĺňa všetky podmienky zo zadania.
Počet riešení (diskusia): Zistíme počet výsledkov, ktoré vyhovujú zadaniu úlohy. Nie vždy musíme všetky výsledky narysovať.
HoreGeometrické konštrukcie: značenie
| Značka | Význam |
|---|---|
| p \parallel q | rovnobežné priamky |
| p \perp q | kolmé priamky |
| \sphericalangle BAC | uhol pri vrchole A |
| \triangle ABC | trojuholník ABC |
| \vert AB\vert | dĺžka úsečky AB |
| A \in p | A leží na priamke p |
| A \notin p | A neleží na priamke p |
| \leftrightarrow AB | priamka prechádzajúca bodmi A, B |
| \mapsto AB | polpriamka začínajúca v bode A, prechádzajúca bodom B |
| \mapsto ABC | polrovina s hraničnou priamkou AB, obsahujúca bod C |
| \mapsto pK | polrovina s hraničnou priamkou p, obsahujúca bod K |
| \leftrightarrow ABC | rovina určená bodmi A, B, C |
| (p, q) | pás roviny, ohraničený rovnobežkami p, q |
Ďalej využívame pre zápis geometrických konštrukcií množinové operácie, predovšetkým prienik (\cap) a zjednotenie (\cup).
HorePolpriamky a polroviny
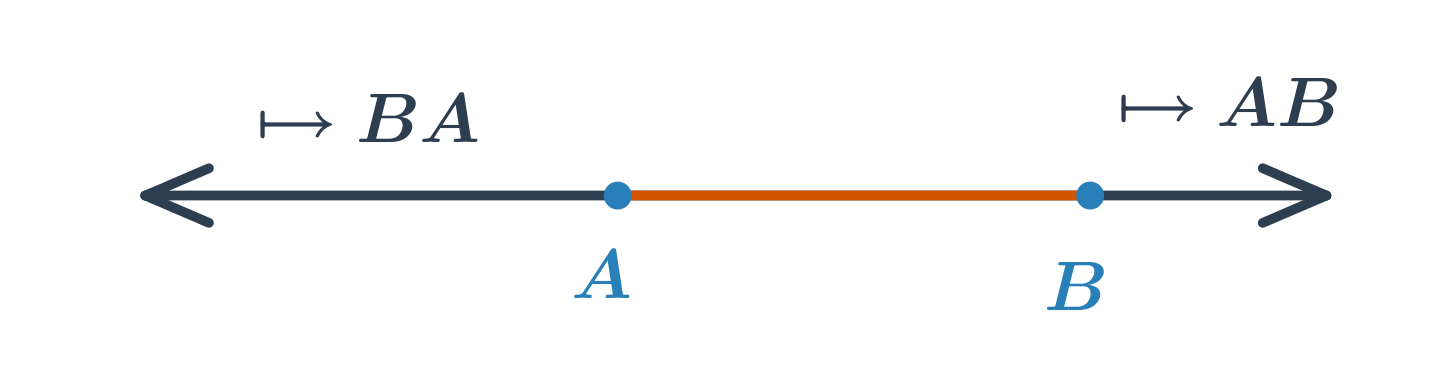
Polpriamka je časť priamky, ktorá vznikne rozdelením priamky jedným jej bodom. Tento bod sa nazýva počiatočný. Polpriamku s počiatočným bodom A prechádzajúcu bodom B značíme \mapsto AB. Každý bod rozdeľuje priamku na dve opačné polpriamky so spoločným počiatočným bodom.
Základné vlastnosti * Zjednotením dvoch opačných polpriamok je priamka. * Prienikom dvoch opačných polpriamok je bod. * Prienikom polpriamok \mapsto AB a \mapsto BA je úsečka AB.
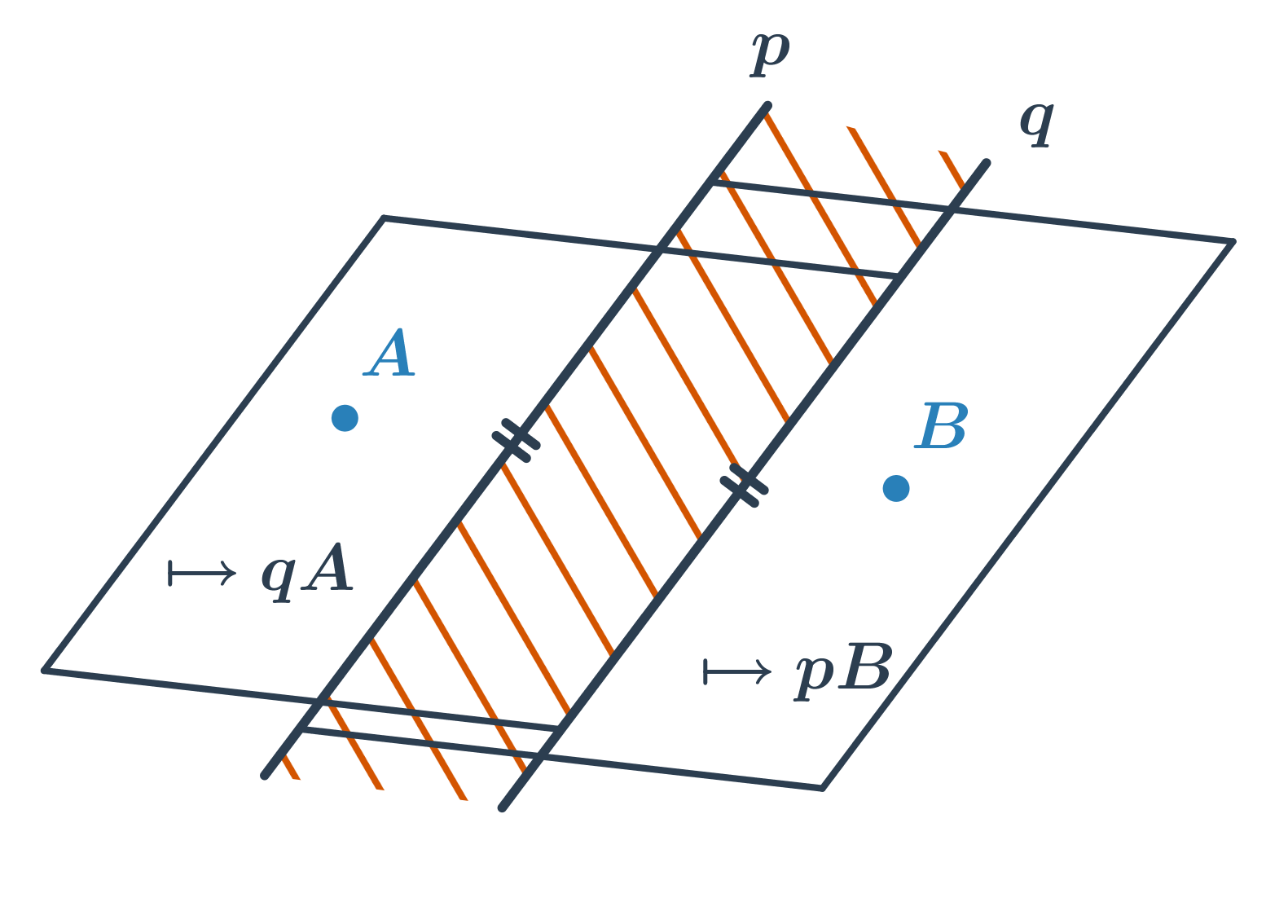
Polrovina je časť roviny, ktorá vznikne rozdelením roviny jednou priamkou. Táto priamka sa nazýva hraničná. Polrovinu s hraničnou priamkou p prechádzajúcu bodom K značíme \mapsto pK. Ak je priamka p určená bodmi A, B, môžeme tiež písať \mapsto ABK. Každá priamka rozdeľuje rovinu na dve opačné polroviny so spoločnou hraničnou priamkou.
Základné vlastnosti * Zjednotením dvoch opačných polrovín je rovina. * Prienikom dvoch opačných polrovín je hraničná priamka. * Prienikom dvoch polrovín s rovnobežnými hraničnými priamkami je pás rovnobežiek.
Pre zápis geometrických konštrukcií používame množinové operácie, hlavne prienik (\cap) a zjednotenie (\cup).
Príklad: Rozhodnite, čo je prienikom polpriamky CA a polroviny ABC.
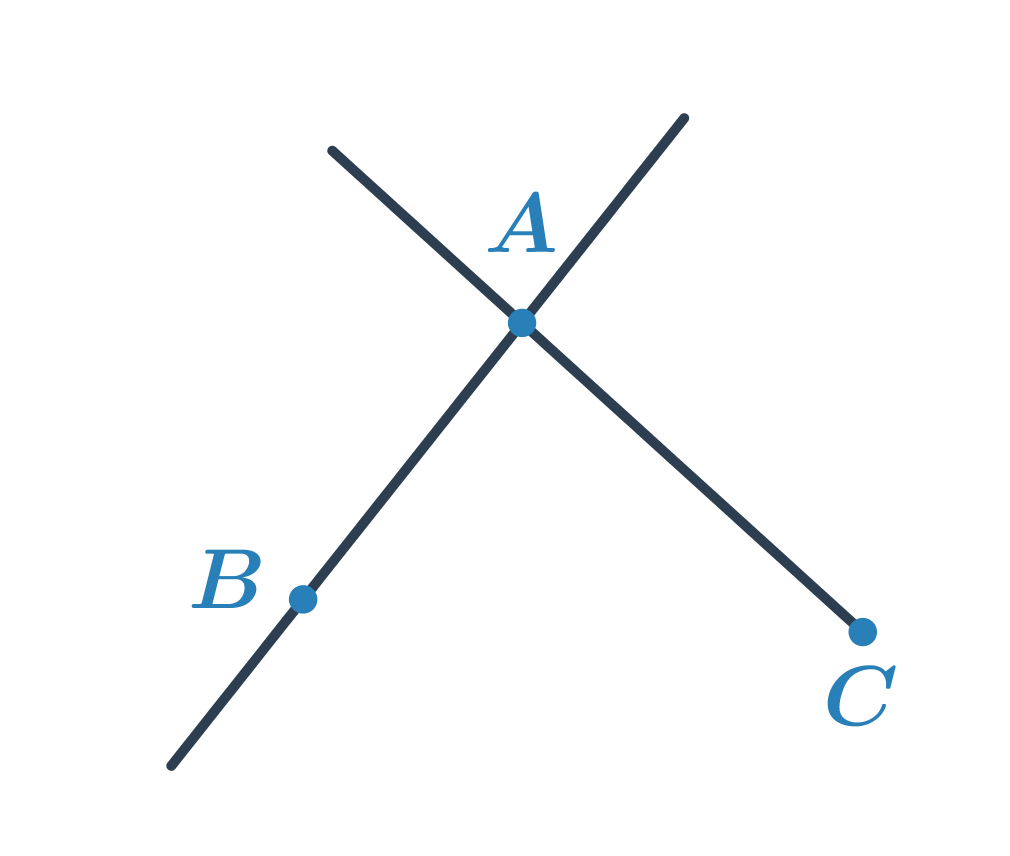
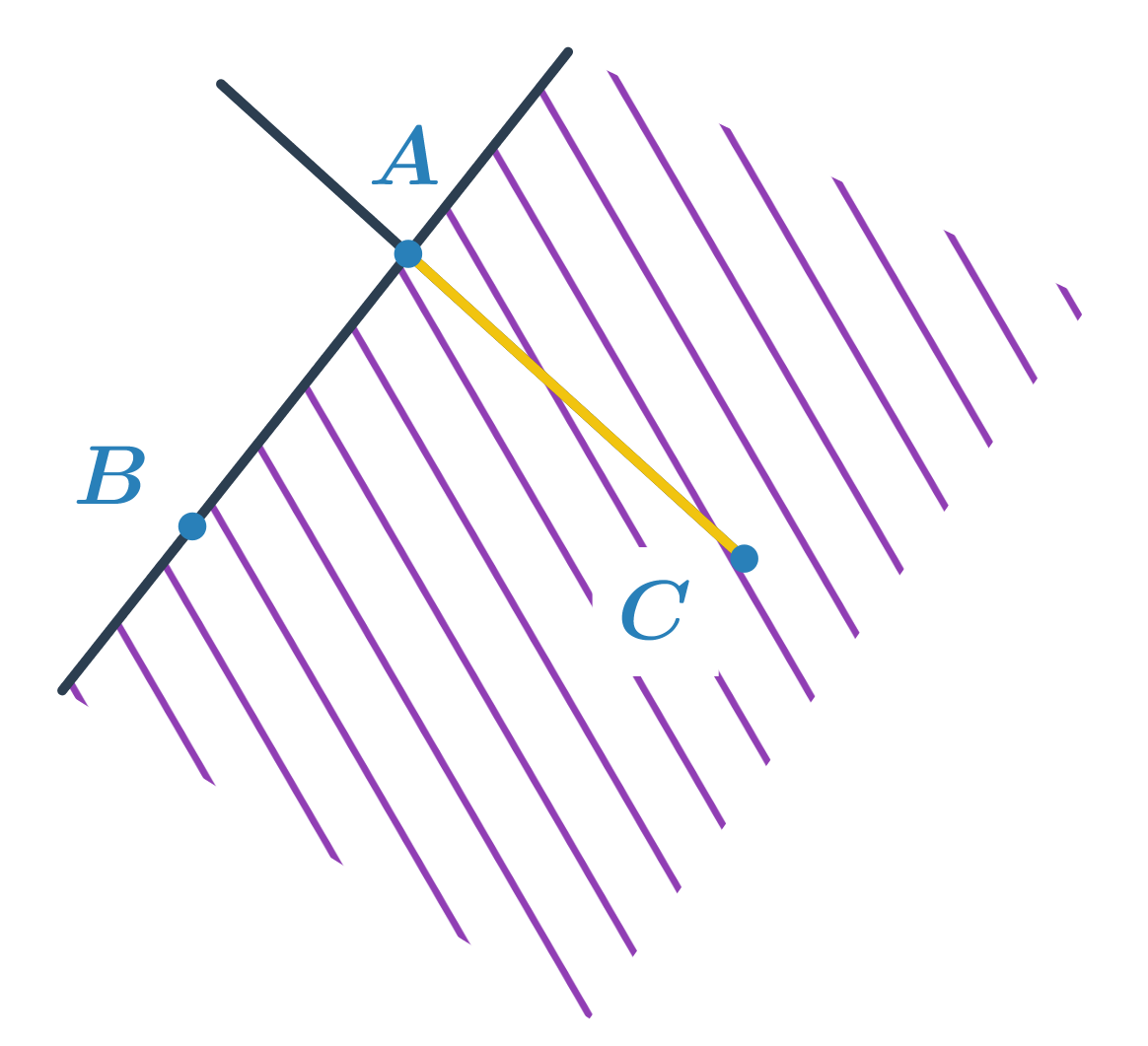
Polrovina ABC je určená hraničnou priamkou AB a bodom C. Polpriamka CA má počiatočný bod C a prechádza bodom A. Prienikom je potom úsečka AC. Matematicky by sme úlohu zapísali: AC = \mapsto ABC \cap \mapsto CA.
Rovnobežky a kolmice
Rovnobežky sú dve priamky ležiace v rovnakej rovine, ktoré sa nikde nepretínajú. Rovnobežnosť priamok p a q zapisujeme p \parallel q.
Kolmica je priamka, ktorá pretína inú priamku a zviera s ňou uhol 90°. Kolmosť priamok p a q zapisujeme p \perp q.
Dve priamky, ktoré sú kolmé na nejakú tretiu priamku a súčasne obe ležia v jednej rovine, sú rovnobežky.
HoreKonštrukčné úlohy: trojuholníky
Pri riešení jednoduchších úloh zostrojujeme trojuholníky, pre ktoré poznáme dĺžky strán. Nesmieme pritom zabúdať, že platí tzv. trojuholníková nerovnosť, teda že súčet dvoch strán je väčší než tretia strana. Jednoducho povedané, ak je súčet dvoch najkratších strán väčší než tretia strana, trojuholník sa dá zostrojiť.
Pri zložitejších príkladoch využívame vety o zostrojiteľnosti trojuholníkov (kde s značí stranu a u uhol):
- Veta sss — v trojuholníku sú dané dĺžky všetkých strán, platí trojuholníková nerovnosť.
- Veta sus — v trojuholníku sú dané dĺžky dvoch strán a veľkosť uhla, ktorý zvierajú (menší než 180°).
- Veta usu — v trojuholníku je daná dĺžka jednej strany a veľkosti 2 uhlov k nej priliehajúcich (súčet veľkostí daných uhlov je menší než 180°).
Tieto vety tiež používame pri určení zhodnosti trojuholníkov.
Pri najťažších príkladoch využívame pri konštrukcii ďalšie pojmy súvisiace s trojuholníkom, napríklad výška, ťažnica, či množiny bodov daných vlastností.
HoreKonstrukčné úlohy prierezovo
Pri riešení zložitejších konštrukčných úloh budeme využívať aj množiny bodov daných vlastností. Pripomeňme si tie najdôležitejšie.
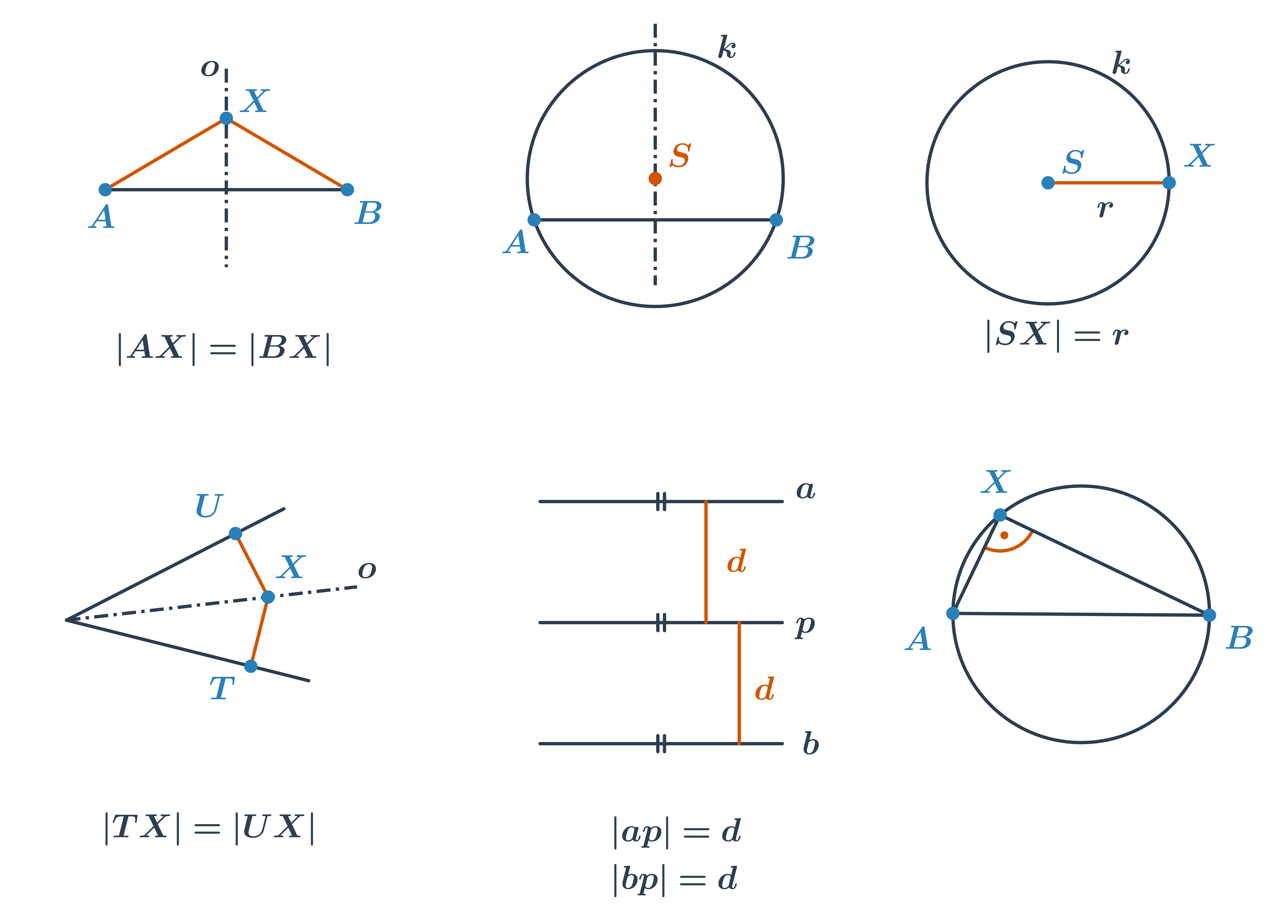
| os úsečky AB | množina všetkých bodov, ktoré majú od bodov A, B rovnakú vzdialenosť |
| os úsečky AB | množina stredov všetkých kružníc, ktoré prechádzajú bodmi A, B |
| kružnica | množina všetkých bodov, ktoré majú od bodu S rovnakú vzdialenosť (polomer r) |
| os uhla | množina všetkých bodov, ktoré majú od ramien uhla rovnakú vzdialenosť |
| rovnobežky | množiny všetkých bodov, ktoré majú od priamky p rovnakú vzdialenosť |
| Tálesova kružnica nad úsečkou AB | množina všetkých vrcholov pravých uhlov, ktorých ramená prechádzajú bodmi A, B |


 Slovenčina
Slovenčina Angličtina
Angličtina Informatika
Informatika Vieme to
Vieme to Nemčina
Nemčina Biológia
Biológia Zemepis
Zemepis Chémia
Chémia Fyzika
Fyzika