Výpis prehľadov
Rovinné útvary
Prechádzate súhrny informácií k určitým témam. Systémy Vieme sa zameriavajú hlavne na ich precvičovanie. K cvičeniam k jednotlivým podtémam sa dostanete pomocou odkazov nižšie.
Podkapitoly
Rovinné útvary
Rovinné útvary sú množiny bodov v rovine, ide teda o dvojrozmerné útvary. Najznámejšie rovinné útvary sú napríklad štvorec, obdĺžnik, trojuholník, kružnica, kruh, rovnobežník, lichobežník, pravidelný alebo nepravidelný mnohouholník.
Pri niektorých rovinných útvaroch dokážeme jednoducho vypočítať ich obvod a obsah.
HoreTrojuholník
Trojuholník je základný geometrický útvar, ktorý má tri vrcholy a tri strany. Trojuholníky hrajú v geometrii kľúčovú rolu, pretože sa veľa problémov dá riešiť tak, že zložitejšie obrazce rozdelíme na trojuholníky a následne pracujeme s nimi.
Značenie strán a uhlov v trojuholníku:
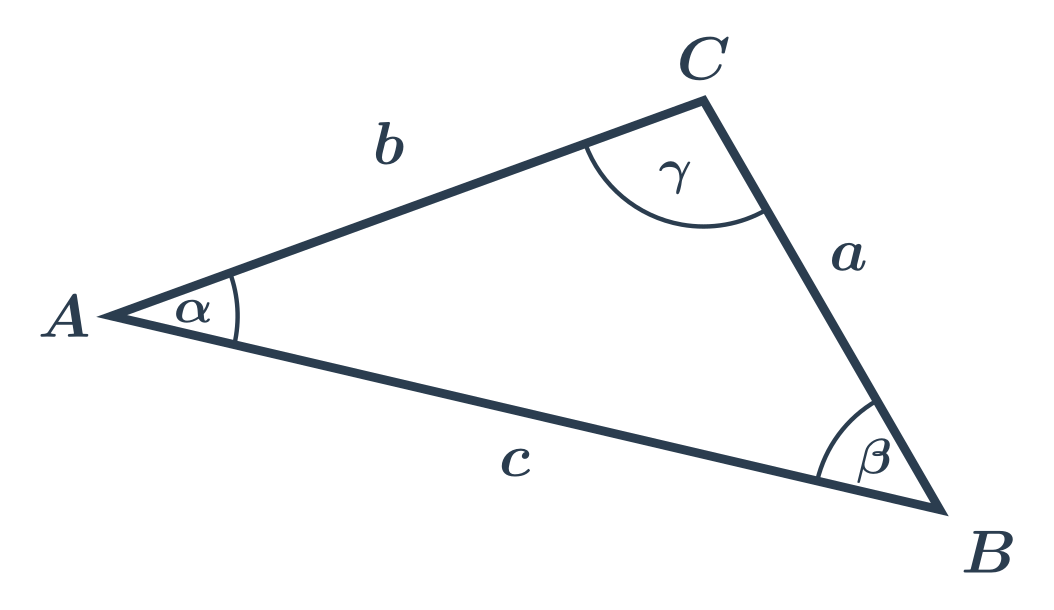
Proti vrcholu A je strana a, proti vrcholu B je strana b a proti vrcholu C je strana c.
Výšky príslušné stranám v trojuholníku:
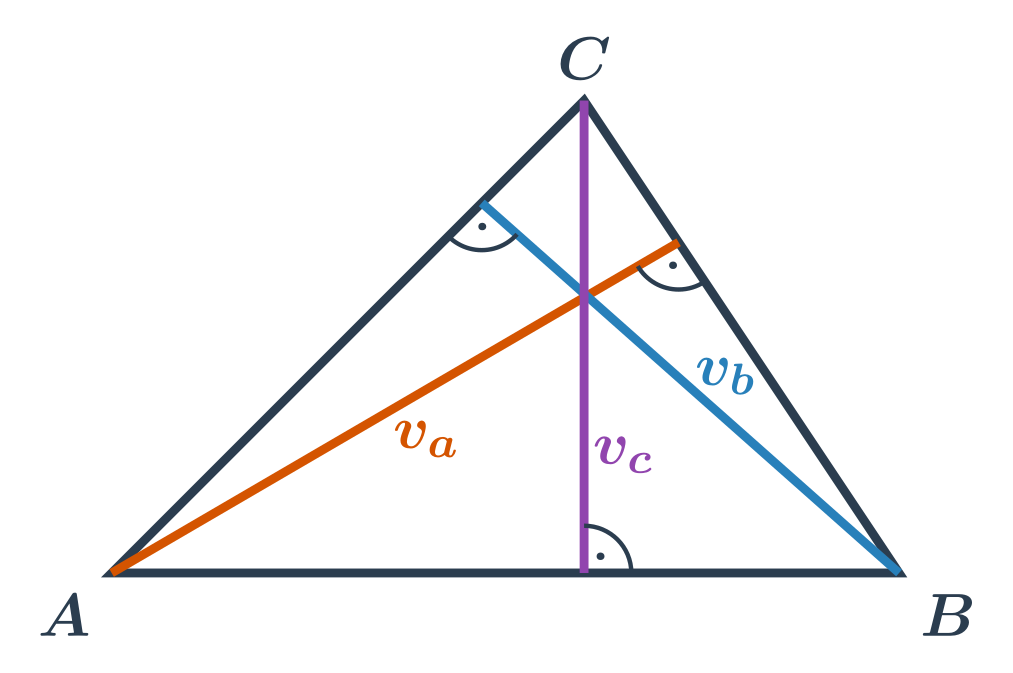
Výška v_a je vzdialenosť bodu A od priamky, na ktorej leží strana a. Teda je to vzdialenosť bodu A od päty kolmice na priamku BC vedenú bodom A. Táto päta kolmice môže a nemusí ležať priamo na strane a.
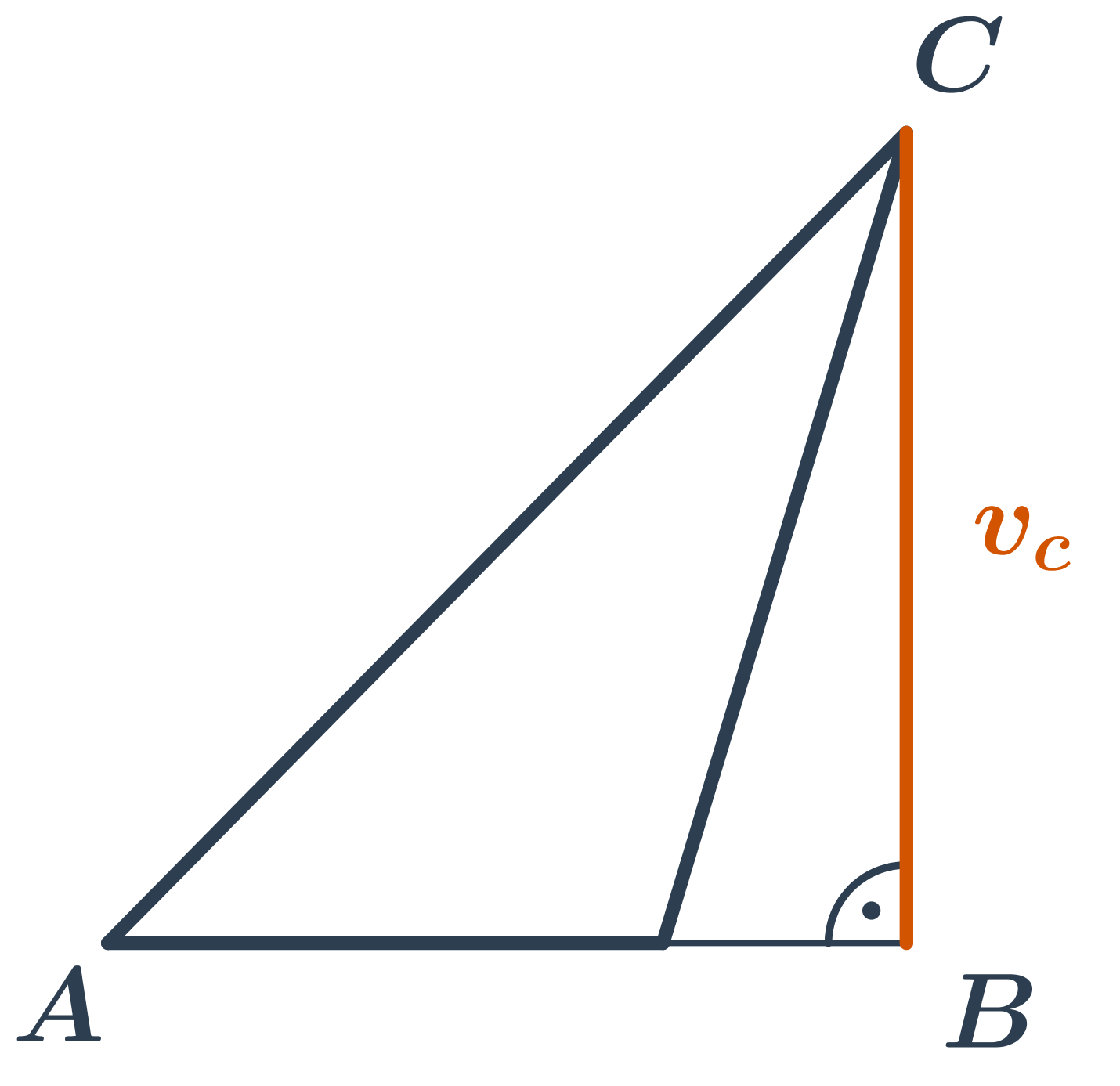
Témy súvisiace s trojuholníkom:
- Pojmy súvisiace s trojuholníkom (napr. rovnoramenný, rovnostranný, výška, dotyčnica, opísaná kružnica)
- Obvod trojuholníka a obsah trojuholníka (výpočty na základe zadaných údajov o trojuholníku)
- Konštrukčné úlohy s trojuholníkmi (narysovanie trojuholníkov na základe zadaných údajov, napr. s využitím viet sss, sus, usu)
- Pytagorova veta, Euklidove vety, goniometrické funkcie – (užitočné vlastnosti pravouhlého trojuholníka)
Pytagorova veta
Pytagorova veta popisuje vzťah, ktorý platí medzi dĺžkami strán pravouhlého trojuholníka. Veta znie: Obsah štvorca zostrojeného nad preponou pravouhlého trojuholníka je rovný súčtu obsahov štvorcov nad obomi jeho odvesnami. Pytagorovu vetu môžeme zapísať vzťahom c^2 = a^2 + b^2, kde c označuje dĺžku prepony pravouhlého trojuholníka a dĺžky odvesien sú a, b.
Nasledujúci obrázok znázorňuje graficky znenie vety a tiež „obrázkový dôkaz“ tejto vety:
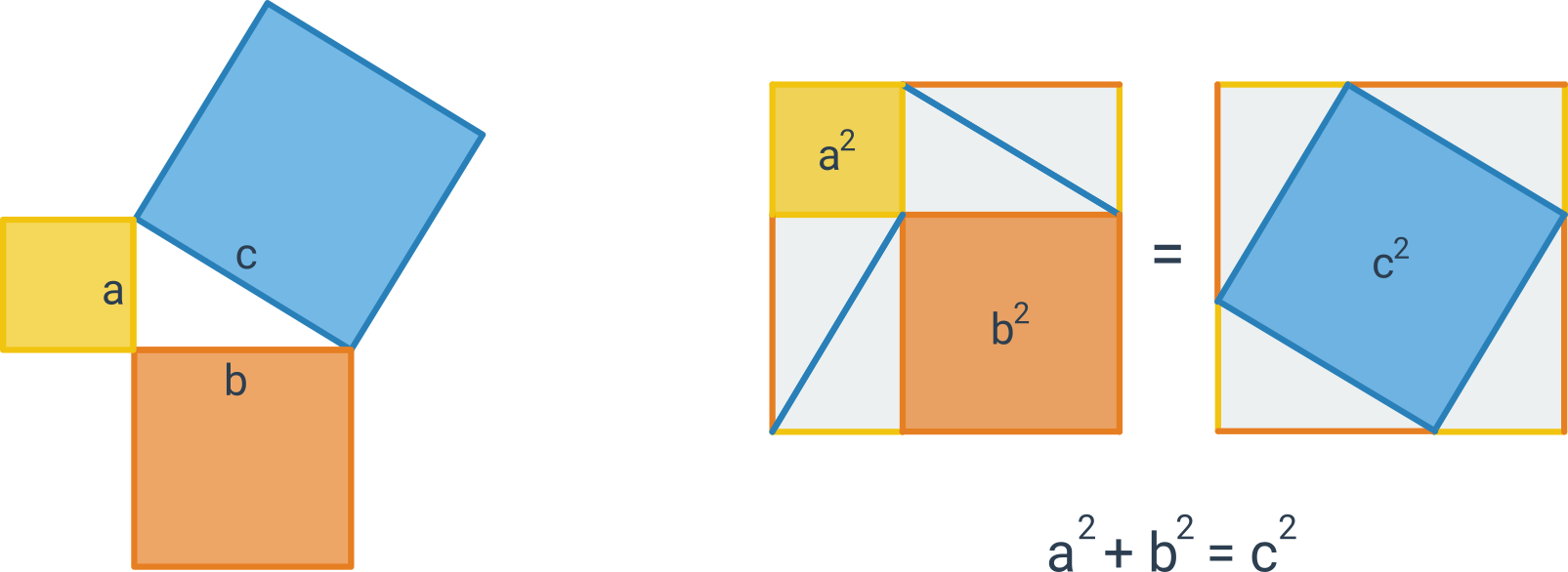
Platí aj opačný smer: Ak má trojuholník strany dĺžok a, b, c, ktoré spĺňajú rovnosť c^2 = a^2 + b^2, potom musí ísť o pravouhlý trojuholník s preponou c.
HorePytagorova veta: základné použitie
Pytagorova veta umožňuje dopočítať dĺžku tretej strany pravouhlého trojuholníka, pri ktorom poznáme dĺžky dvoch zvyšných strán:
Dĺžka odvesny c = \sqrt{a^2 + b^2}. Ak má pravouhlý trojuholník odvesny s dĺžkou 3 metre a 6 metrov, prepona má dĺžku \sqrt{3^2+6^2} = \sqrt{9+36} = \sqrt{45} \doteq 6,41 metra.
Dĺžka prepony a = \sqrt{c^2-b^2}. Ak má trojuholník preponu s dĺžkou 8 metrov a jedna z odvesien má dĺžku 4 metre, druhá odvesna má dĺžku \sqrt{8^2-4^2} = \sqrt{64-16} = \sqrt{48} \doteq 6,93 metra.
Pytagorejské trojice sú trojice celých čísel, ktoré spĺňajú a^2+b^2=c^2, teda trojuholník s príslušnými dĺžkami strán je pravouhlý. Typickým príkladom pytagorejskej trojice je (3, 4, 5): 3^2 + 4^2 = 9+16 = 25 = 5^2.
Ďalšie príklady pytagorejských trojíc: (5, 12, 13); (8, 15, 17); (7, 24, 25); (20, 21, 29); (9, 40, 41). Medzi pytagorejské trojice patria tiež všetky násobky týchto trojíc, napr. (6, 8, 10); (9, 12, 15); (10, 24, 26). Ak si zapamätáme niektoré základné pytagorejské trojice, predovšetkým najjednoduchšiu trojicu (3, 4, 5), tak nám to môže uľahčiť výpočty.
HorePytagorova veta: aplikácie
Pytagorova veta má v geometrii veľmi široké využitie, pretože môžeme veľa zložitejších útvarov rozložiť na pravouhlé trojuholníky.
Typickým príkladom aplikácie Pytagorovej vety je výpočet dĺžky uhlopriečky štvorca alebo výšky rovnostranného trojuholníka:
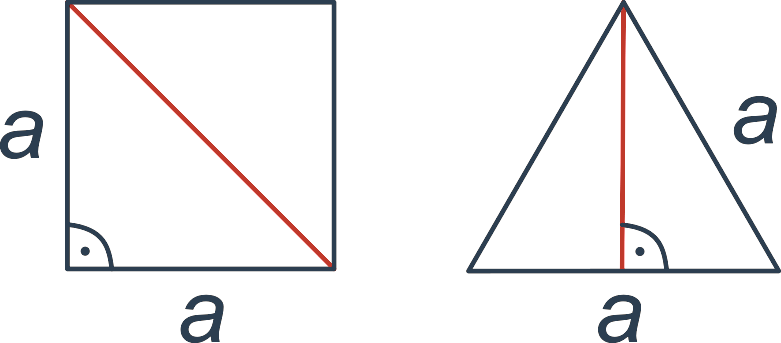
V prípade štvorca so stranou a tvorí uhlopriečka preponu pravouhlého trojuholníka s odvesnami s dĺžkou a. Pre dĺžku uhlopriečky u teda platí u^2 = a^2 + a^2. Po úpravách: u = \sqrt{a^2+a^2} = \sqrt{2a^2} = a\sqrt{2}. Napríklad štvorec so stranou 10 cm má teda uhlopriečku s dĺžkou 10\cdot \sqrt{2} \doteq 14,1 metra.
V prípade rovnostranného trojuholníka so stranou a tvorí výška odvesnu pravouhlého trojuholníka s preponou s dĺžkou a a odvesnou s dĺžkou \frac{a}{2}. Pre dĺžku výšky v teda platí v^2 + \large(\frac{a}{2}\large)^2 = a^2. Po úpravách dostávame v^2 = a^2 - \frac{a^2}{2^2} = \frac{3}{4}a^2, v = a\frac{\sqrt{3}}{2}. Napríklad v rovnostrannom trojuholníku so stranou 5 metrov má teda výška dĺžku \frac{\sqrt{3}}{2}\cdot 5 \doteq 4,33 metra.
HoreEuklidove vety
Euklidove vety sú dve tvrdenia o vlastnostiach pravouhlého trojuholníka.
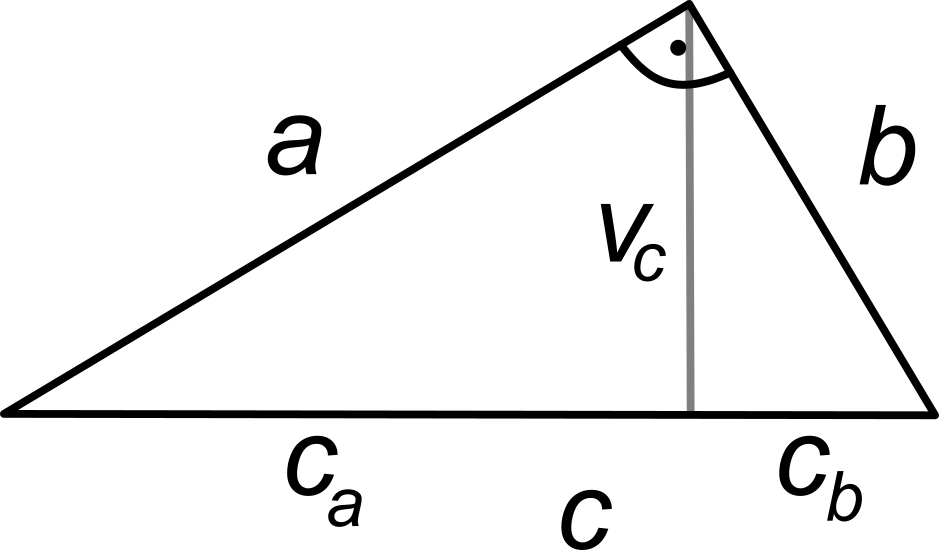
Euklidova veta o výške
Obsah štvorca zostrojeného nad výškou pravouhlého trojuholníka sa rovná obsahu obdĺžnika zostrojeného z oboch úsekov prepony:
v_c^2 = c_a\cdot c_b
Euklidova veta o odvesne
Obsah štvorca zostrojeného nad odvesnou pravouhlého trojuholníka sa rovná obsahu obdĺžnika zostrojeného z prepony a úseku prepony priľahlej k tejto odvesne.
- a^2 = c\cdot c_a
- b^2 = c\cdot c_b
Štvorec a obdĺžnik
Obdĺžnik patrí medzi štvoruholníky. Je to rovnobežník, ktorý má všetky vnútorné uhly pravé.
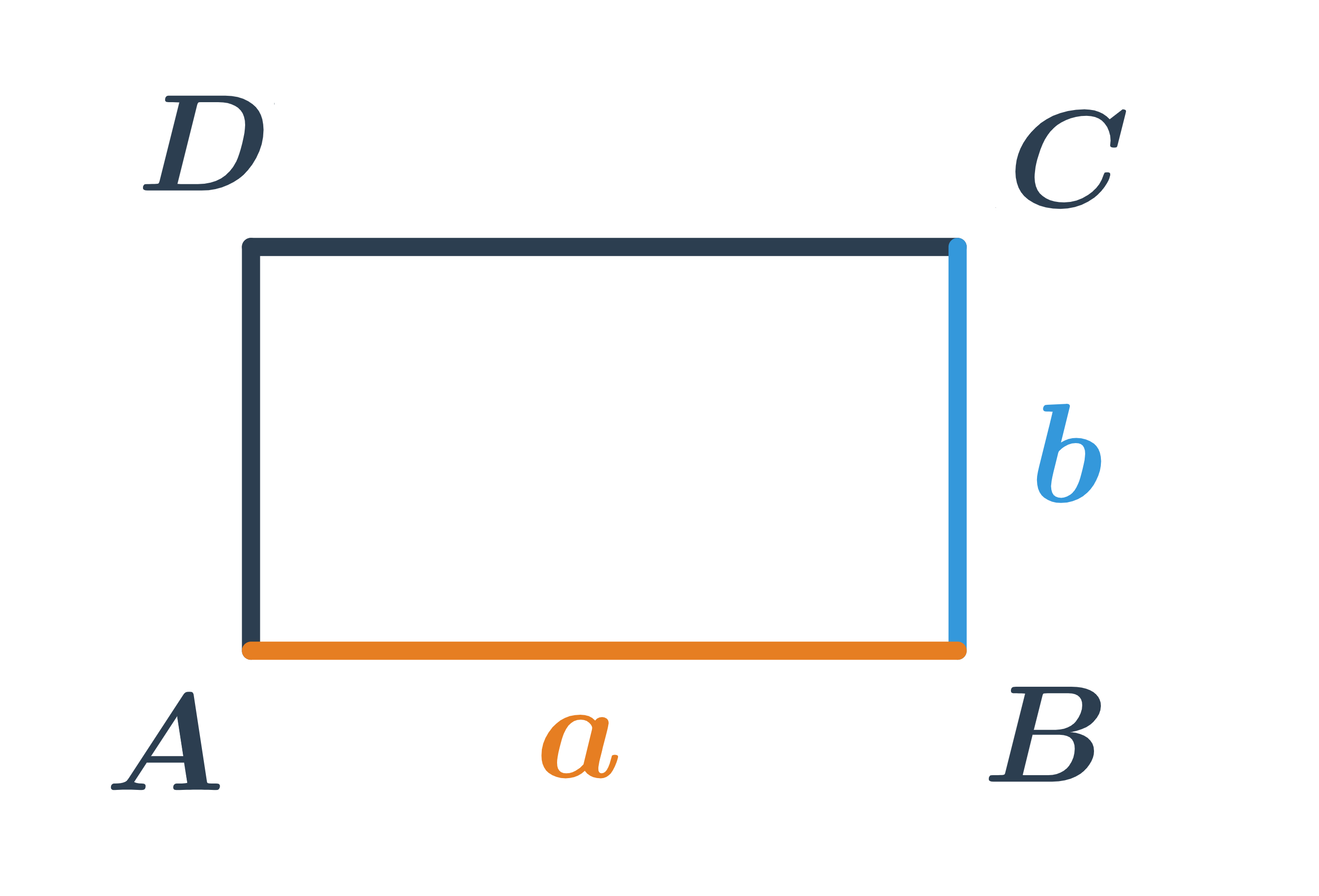
Štvorec je zvláštny prípad obdĺžnika, ktorý má všetky strany rovnako dlhé.
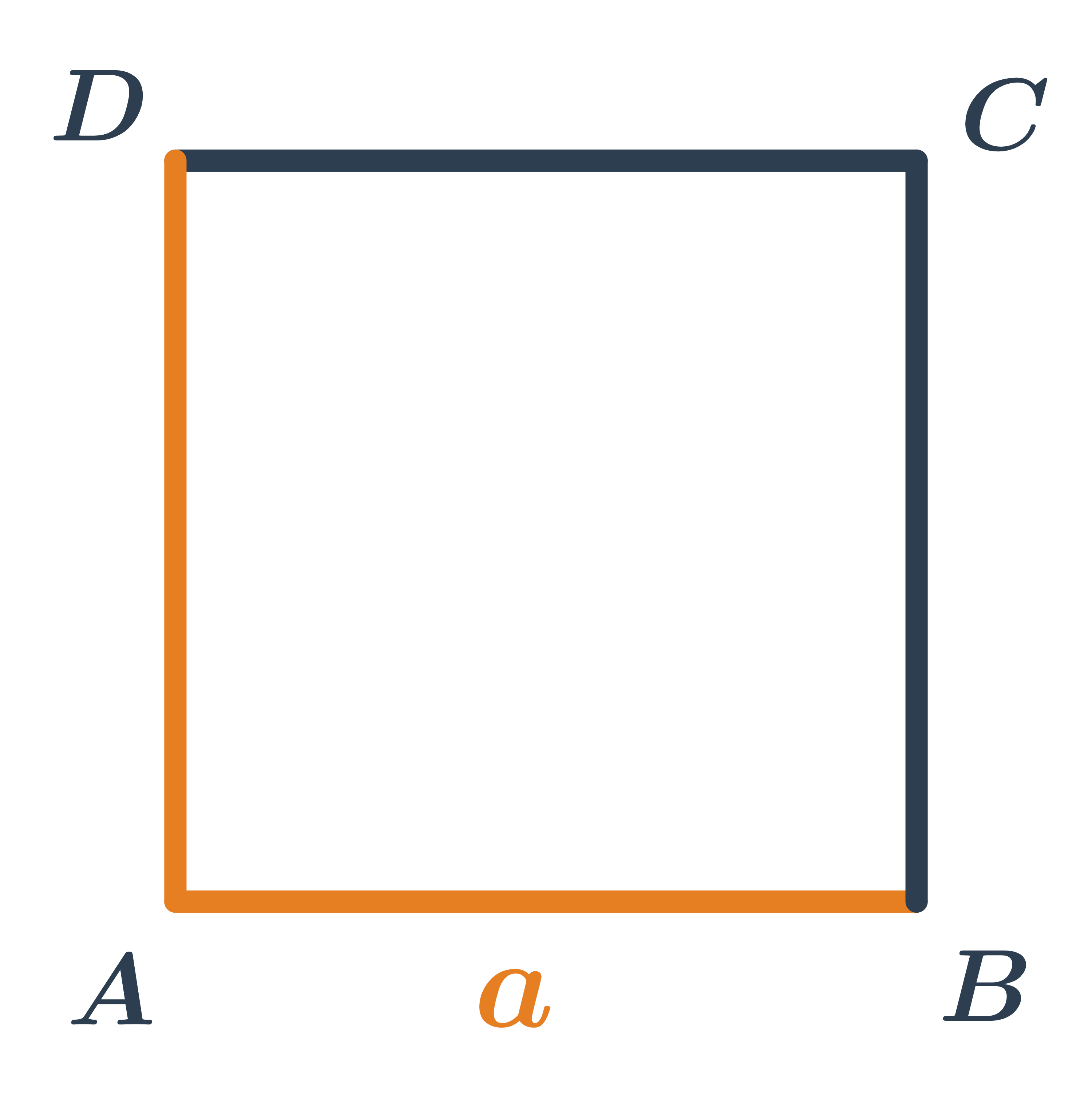
Rovnobežník
Rovnobežník je štvoruholník, ktorého protiľahlé strany sú rovnobežné. Kedysi sa označoval tiež ako kosodĺžnik.
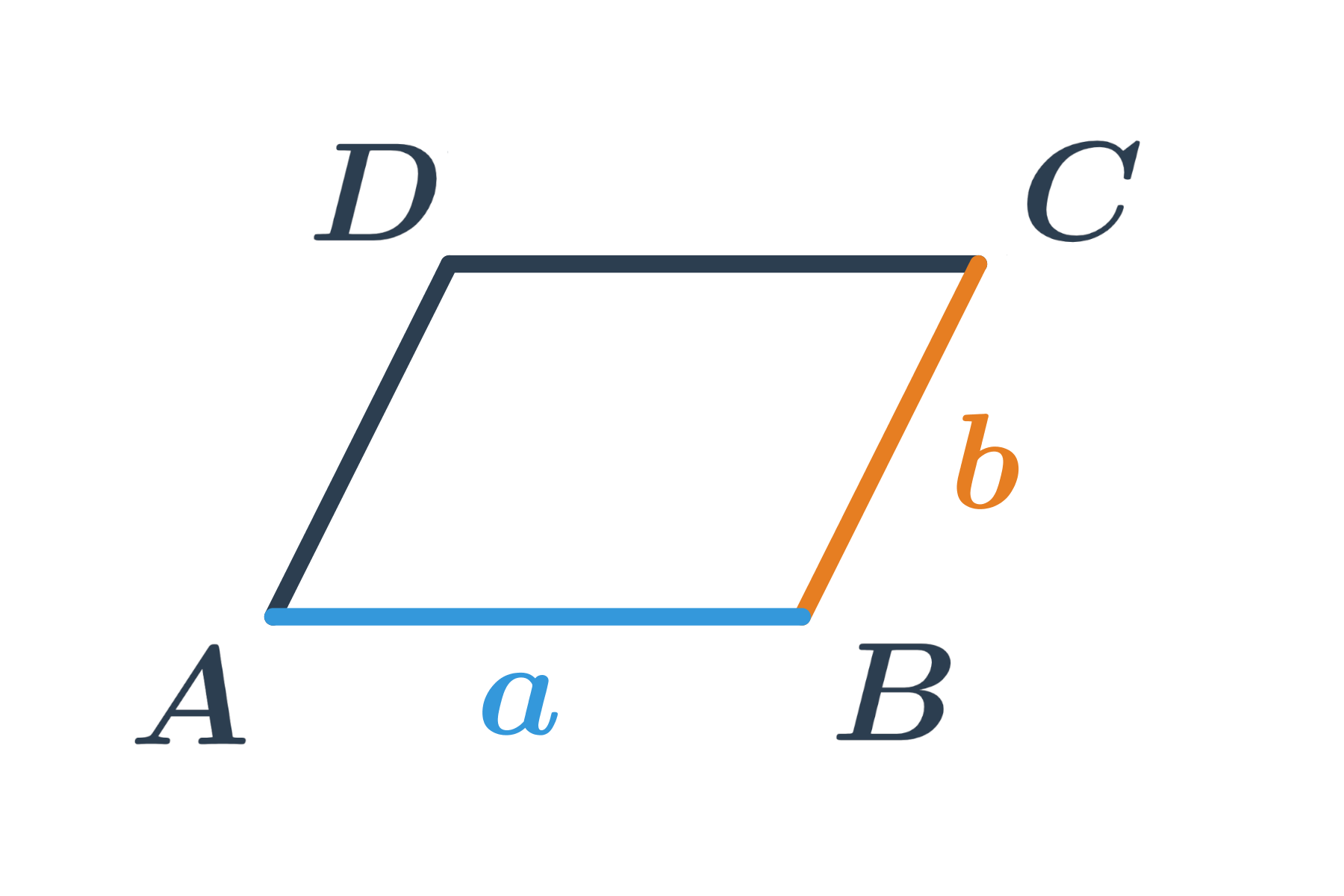
Špeciálne prípady rovnobežníka:
- Kosoštvorec má všetky strany rovnako dlhé.
- Obdĺžnik má vnútorné uhly pravé.
- Štvorec má vnútorné uhly pravé a všetky strany rovnako dlhé.
Lichobežník
Lichobežník je štvoruholník, ktorého dve protiľahlé strany sú rovnobežné (hovoríme im základne) a zvyšné dve protiľahlé strany sú rôznobežné.
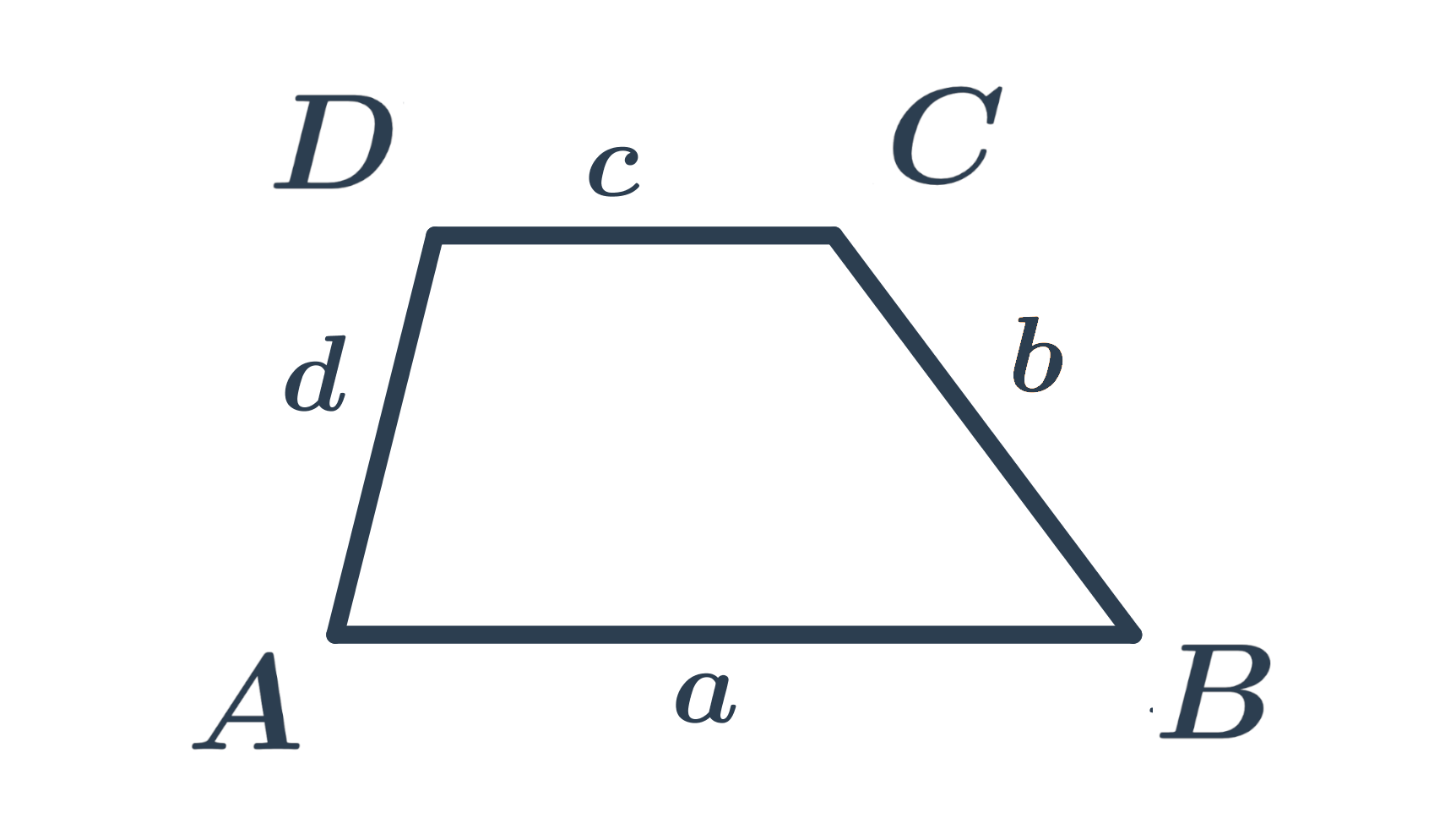
Pravouhlý lichobežník má dva z vnútorných uhlov pravé (základne lichobežníka sú rovnobežné, ak je jeden vnútorný uhol pravý, musí byť jeho doplnok do 180^{\circ} pri druhej základni tiež pravý).
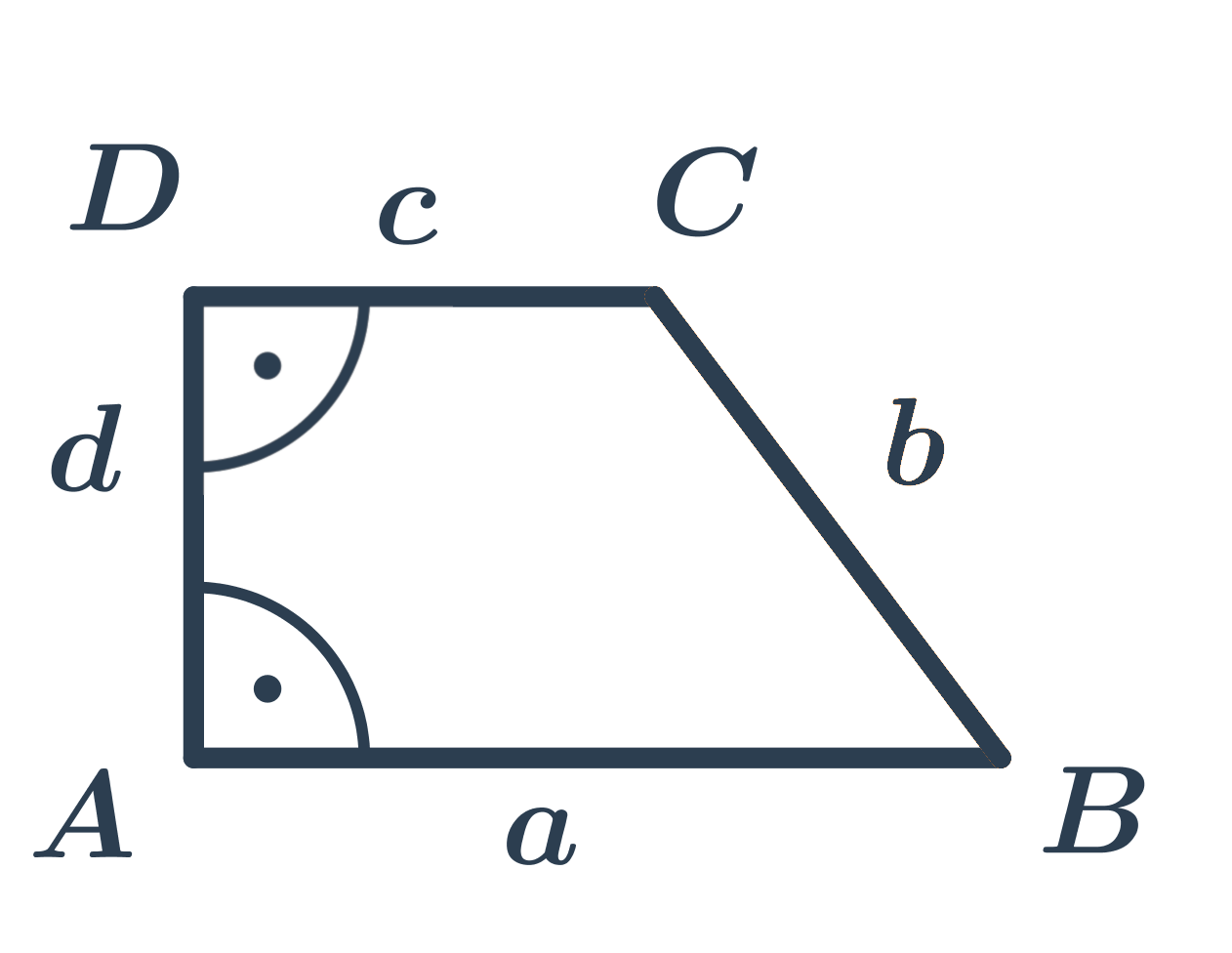
Rovnoramenný lichobežník má ramená rovnakej dĺžky.
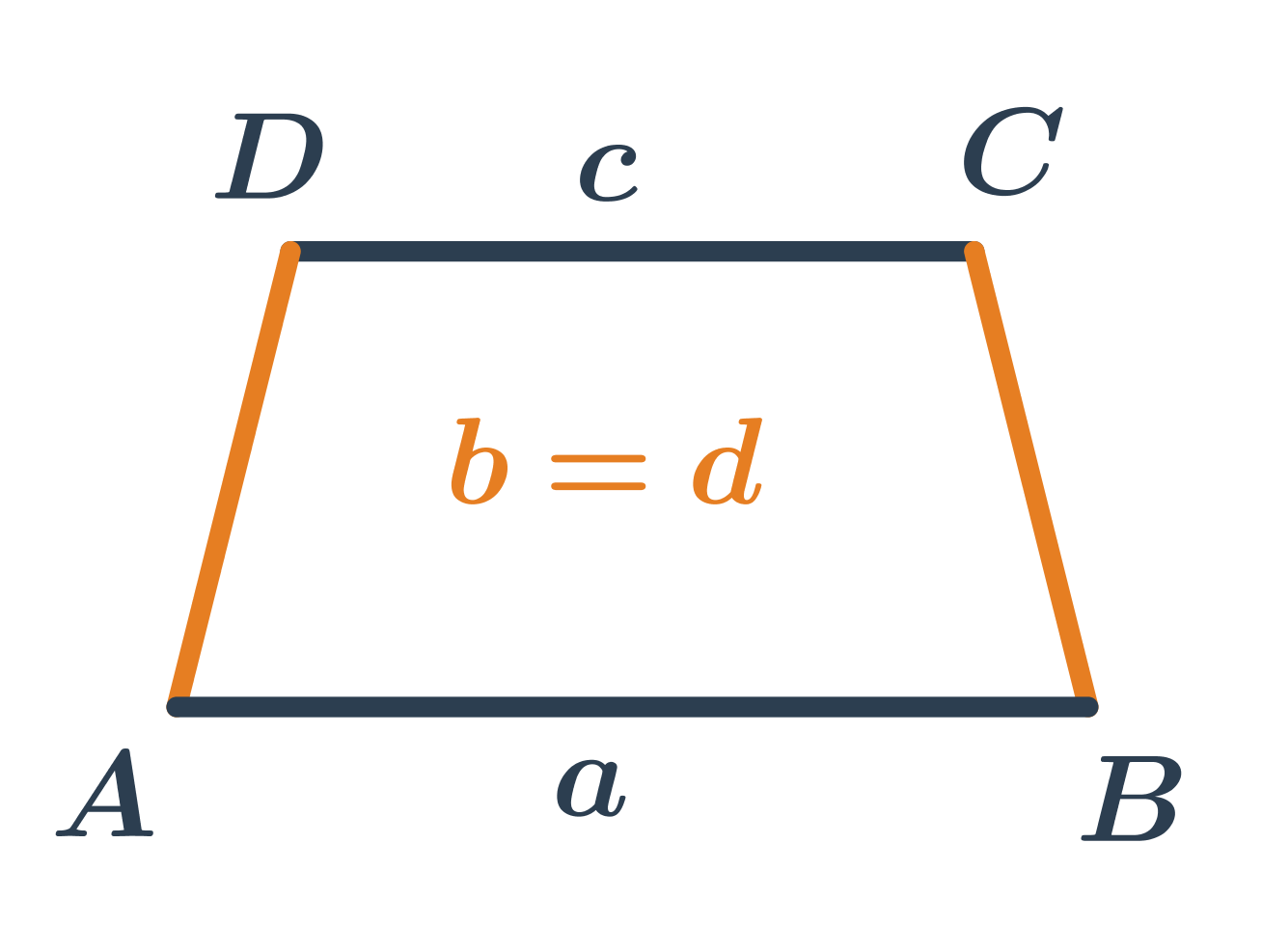
Kruh a kružnica
Kružnica s daným stredom S a polomerom r je tvorená všetkými bodmi v rovine, ktoré sú od stredu vzdialené presne o r. V prípade každého bodu v rovine potom môžeme určiť, kde ležia:
- na kružnici (ich vzdialenosť od S je rovná r)
- vo vnútornej oblasti kružnice (ich vzdialenosť od S je menšia než r, tieto body neležia na kružnici)
- vo vnútornej oblasti kružnice (ich vzdialenosť od S je väčšia než r, tieto body tiež neležia na kružnici)
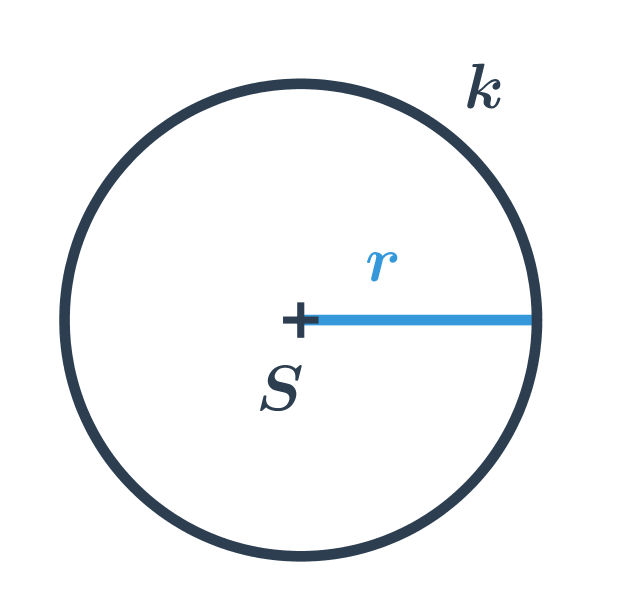
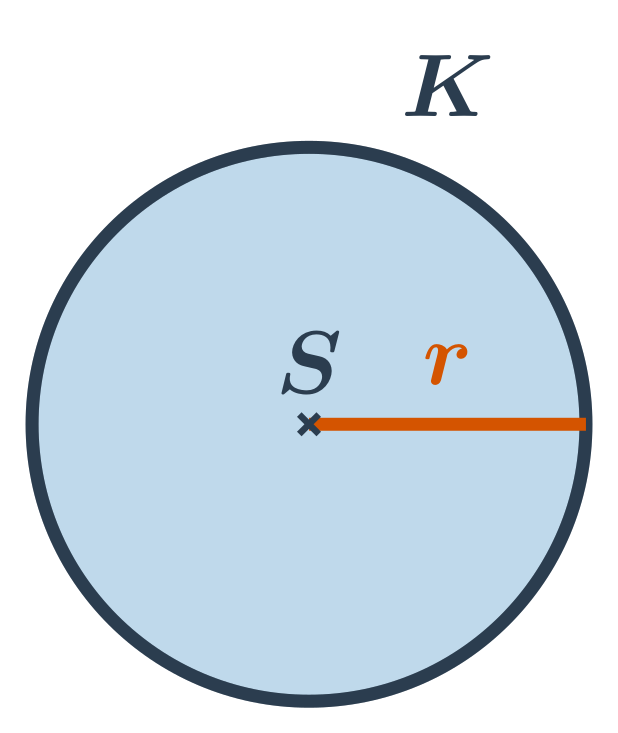
Kruh s daným stredom S a polomerom r je tvorený všetkými bodmi v rovine, ktoré sú od stredu vzdialené najviac o r. Kruh s daným stredom a polomerom je teda zjednotenie kružnice s rovnakým stredom a polomerom a jej vnútornou oblasťou. Stred S kruhu je bod, ktorý patrí do kruhu. (Zatiaľ čo stred kružnice neleží na kružnici, ale v jej vnútornej oblasti.)


 Slovenčina
Slovenčina Angličtina
Angličtina Informatika
Informatika Vieme to
Vieme to Nemčina
Nemčina Biológia
Biológia Zemepis
Zemepis Chémia
Chémia Fyzika
Fyzika