Výpočty so zlomkami

Základné výpočty so zlomkami sú nasledujúce:

Krátenie zlomkov

• Zlomky sa krátia tak, že čitateľ aj menovateľ vydelíme ich spoločným deliteľom.
• Zlomok \frac{9}{12} môžeme skrátiť na \frac{3}{4}, pretože čitateľ aj menovateľ majú spoločný deliteľ 3.

Sčítanie a odčítanie zlomkov

• Pre sčítanie a odčítanie zlomkov je nutné previesť zlomky na spoločný menovateľ.
• \frac{1}{4} + \frac{1}{6} prevedieme na spoločný menovateľ 12 a dostaneme \frac{3}{12} + \frac{2}{12} = \frac{5}{12}.

Násobenie a delenie zlomkov

• Násobenie sa vykonáva tak, že vynásobíme čitateľ aj menovateľ medzi sebou.
• \frac{2}{3} \cdot \frac{3}{4} = \frac{6}{12} = \frac{1}{2}
• Delenie sa vykonáva násobením prevráteného zlomku.
• \frac{2}{3} : \frac{3}{4} = \frac{2}{3} \cdot \frac{4}{3} = \frac{8}{9}

Zlomky a percentá

• Prevod zlomku na percentá sa vykonáva pomocou násobenia 100.
• \frac{3}{4} = 0{,}75 = 75 \%

Zlomky a desatinné čísla

• Zlomky prevedieme na desatinné čísla tak, že čitateľ vydelíme menovateľom. Naopak desatinné číslo je možné previesť na zlomok pomocou roznásobenie mocninami desiatky.
• \frac{2}{5} = 2 : 5 = 0{,}4
• 0{,}25 = 0{,}25 \cdot\frac{100}{100} = \frac{25}{100}, čo po skrátení dáva \frac{1}{4}

Kombinácie operácií so zlomkami

• Zadania kombinujúce rôzne aritmetické operácie so zlomkami.

Rovnakú hodnotu môžeme vyjadriť mnohými zlomkami, napríklad \frac23 = \frac46 = \frac{10}{15} = \frac{200}{300}. Len jedno možné vyjadrenie však považujeme za základný tvar. Zlomok je v základnom tvare, ak sú čitateľ a menovateľ nesúdeliteľné, nemajú teda žiadny spoločný deliteľ okrem jednotky. V uvedenom príklade je v základnom tvare zlomok \frac23.

Ako krátenie zlomku sa označuje operácia, kedy čitateľ a menovateľ vydelíme rovnakým, nenulovým číslom. Krátenie zachováva hodnotu zlomku. Ak chceme zlomok previesť do základného tvaru, krátime najväčším spoločným deliteľom čitateľa a menovateľa.

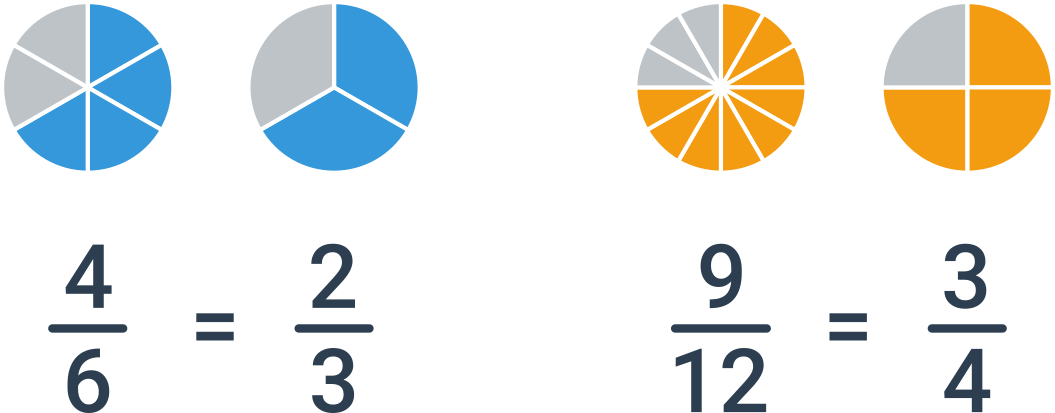
Príklady

• Zlomok \frac{15}{28} je v základnom tvare, pretože čísla 15 a 28 nemajú spoločný deliteľ (sú nesúdeliteľné).

• Zlomok \frac{25}{30} môžeme krátiť číslom 5, čím dostaneme zlomok \frac{5}{6}, ktorý je v základnom tvare.

• Zlomok \frac{12}{18} môžeme krátiť číslom 2, čím dostaneme zlomok \frac{6}{9}. Ak chceme krátiť na základný tvar, nájdeme najväčší spoločný deliteľ čísel 12 a 18, čo je 6. Po krátení číslom 6 dostávame zlomok \frac{2}{3}.

Než sa pustíme do sčítania zlomkov, je dobré mať jasno v tom, čo je čitateľ („to hore“) a menovateľ („to dole“). V zlomku \frac{3}{7} je 3 čitateľ, 7 menovateľ.

Sčítanie zlomkov s rovnakým menovateľom

Ak majú sčítané zlomky rovnaké menovatele, stačí jednoducho sčítať čitatele. Menovateľ necháme rovnaký, teda \frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}.

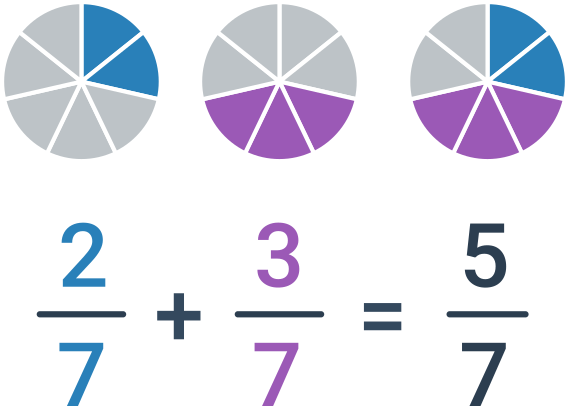
Sčítanie zlomkov s rôznymi menovateľmi

Ak majú sčítané zlomky rôzne menovatele, musíme ich najskôr rozšíriť tak, aby mali rovnaký menovateľ. Najvýhodnejšie je rozšíriť zlomky na najmenší spoločný násobok pôvodných menovateľov. Keď už majú zlomky rovnaký menovateľ, sčítame ich vyššie uvedeným postupom.

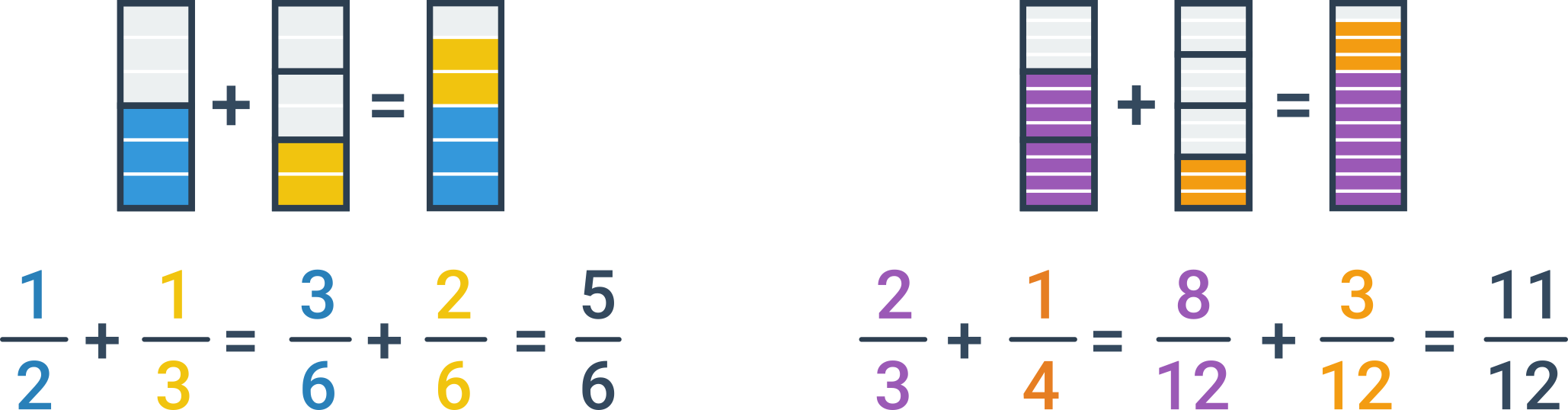
Úpravy a odčítanie

Výsledný zlomok väčšinou ešte krátime, aby sme dostali výsledok v základnom tvare. Odčítanie zlomkov funguje rovnakým spôsobom.

Príklady

• Príklad s rovnakým menovateľom, bez nutnosti krátenia:
  \frac{2}{5}+\frac{1}{5} = \frac{2+1}{5} = \frac{3}{5}.

• Príklad s rovnakým menovateľom, kedy výsledok krátime:
  \frac{5}{6}-\frac{1}{6} = \frac{5-1}{6} = \frac{4}{6} = \frac{2}{3}.

• Príklad s rôznymi menovateľmi: \frac{5}{6} - \frac{3}{4}. Najmenší spoločný násobok menovateľov 6 a 4 je 12, rozšírime teda zlomky na menovateľ 12:
  \frac{5}{6} - \frac{3}{4} = \frac{5\cdot 2}{6\cdot 2} - \frac{3\cdot 3}{4\cdot 3}= \frac{10}{12} - \frac{9}{12} = \frac{1}{12}

Násobenie zlomkov si môžeme predstaviť s pomocou čokolády. Ak násobíme \frac45\cdot \frac23 je to ako keby sme brali štyri z piatich stĺpčekov a dva z troch riadkov. Koľko štvorčekov čokolády takto vezmeme? Osem z pätnástich, teda \frac{8}{15}.

Pri násobení zlomkov teda jednoducho vynásobíme čitateľ prvého zlomku a čitateľ druhého zlomku a dostaneme výsledný čitateľ, podobne pre menovateľ: \frac{a}{b}\cdot \frac{c}{d} = \frac{a\cdot c}{b\cdot d}. Ak sa chceme vyhnúť násobeniu veľkých čísel, môžeme zlomky krátiť, a to aj „do kríža“. Príklady:

• \frac{2}{3}\cdot\frac{1}{5} = \frac{2\cdot 1}{3\cdot 5}=\frac{2}{15}
• \frac{2}{3}\cdot\frac{3}{4} = \frac{2\cdot 3}{3\cdot 4}=\frac{2}{4}=\frac{1}{2} (všimnite si, že neroznásobujeme, ale hneď krátime)

Delenie zlomkov je to isté ako násobenie prevráteným zlomkom: \frac{a}{b}:\frac{c}{d} = \frac{a}{b}\cdot\frac{d}{c}=\frac{a\cdot d}{b\cdot c}. Príklady:

• \frac13:\frac12 =\frac13\cdot \frac21 = \frac23
• \frac{2}{5}:\frac{3}{4}=\frac{2}{5}\cdot \frac{4}{3} = \frac{2\cdot 4}{5\cdot 3} = \frac{8}{15}