Predchádzajúce
Nadväzujúce
Cvičenie
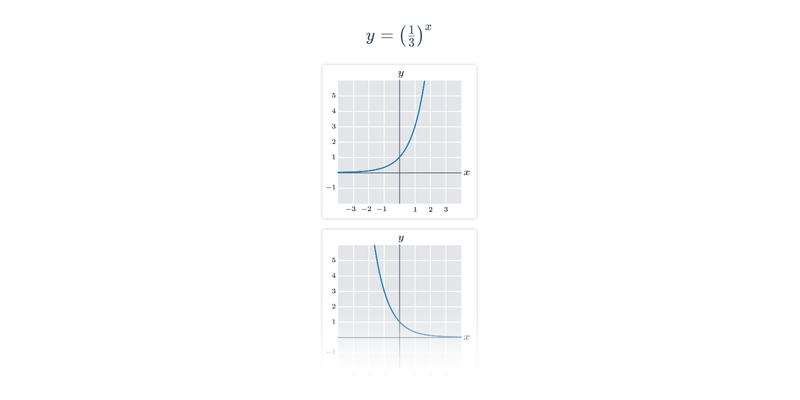
Grafy exponenciálnych funkcií
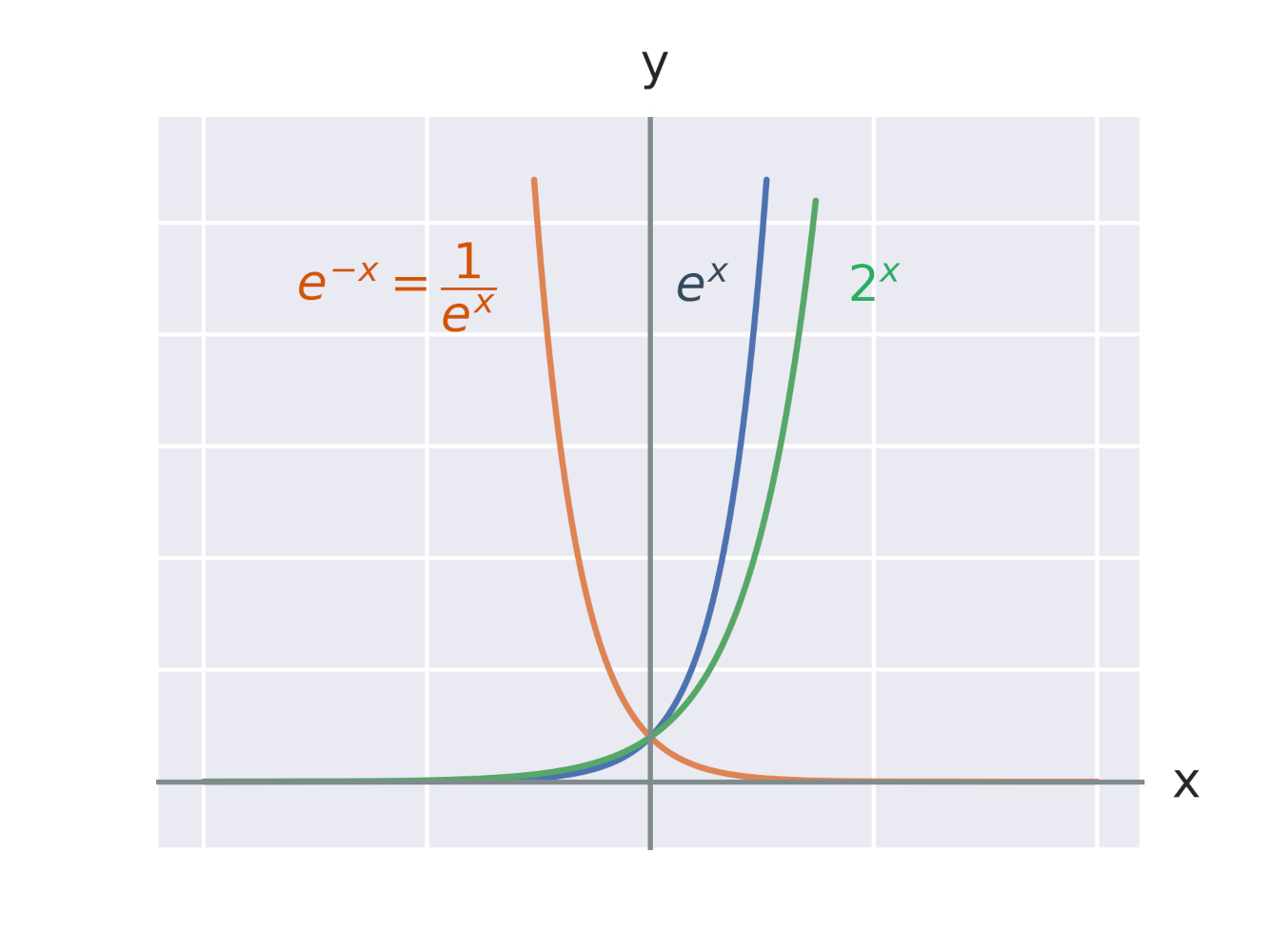
Grafom exponenciálnej funkcie je krivka s názvom exponenciála. Na obrázku sú grafy exponenciálnych funkcií so základmi 2 a e = 2{,}7 182 818 284\ldots. Vidíme tiež, že grafy funkcií e^x a e^{-x} sú spolu súmerné podľa osi y.
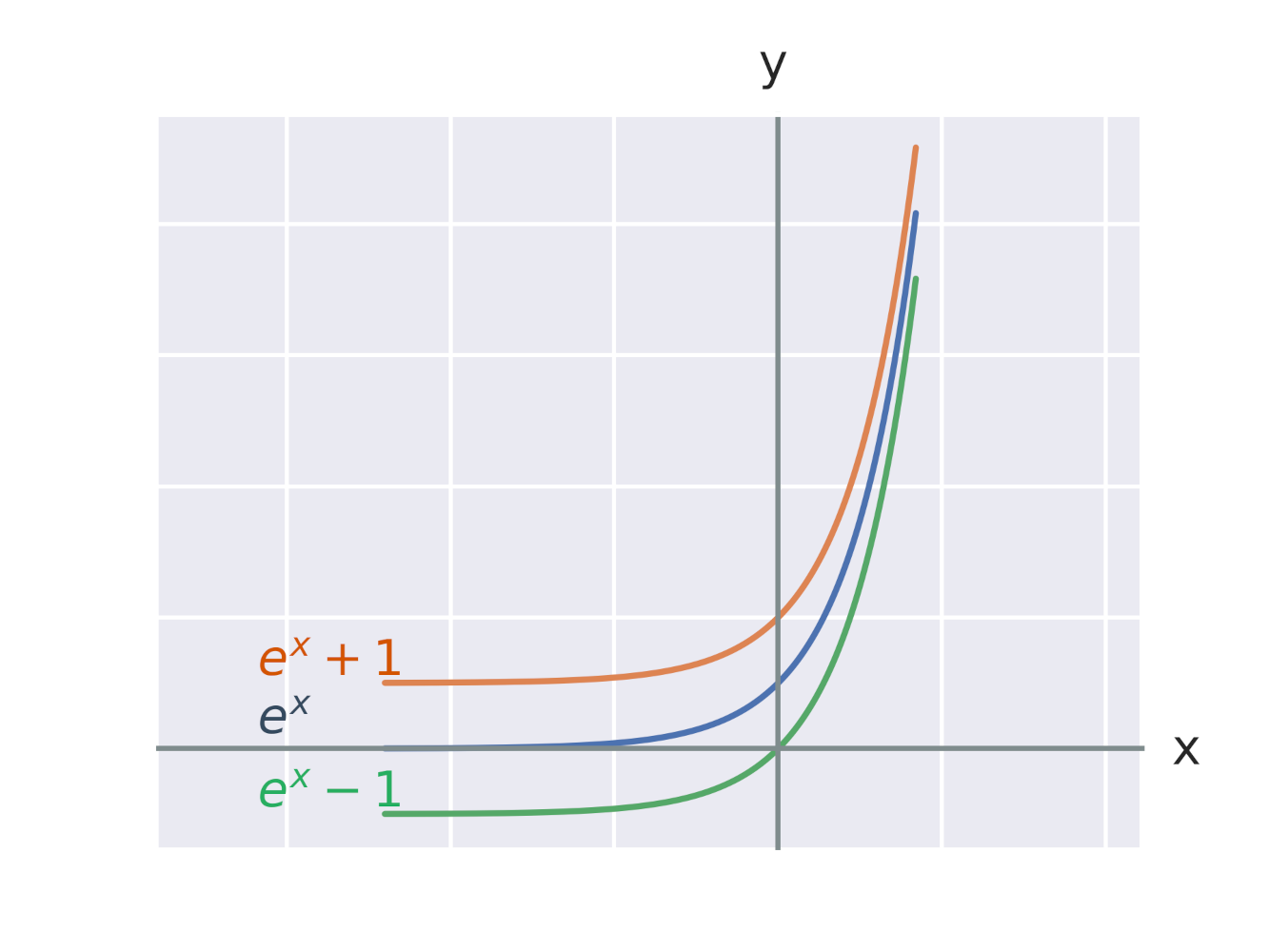
Efekt pripočítania konštanty k exponenciálnej funkcii
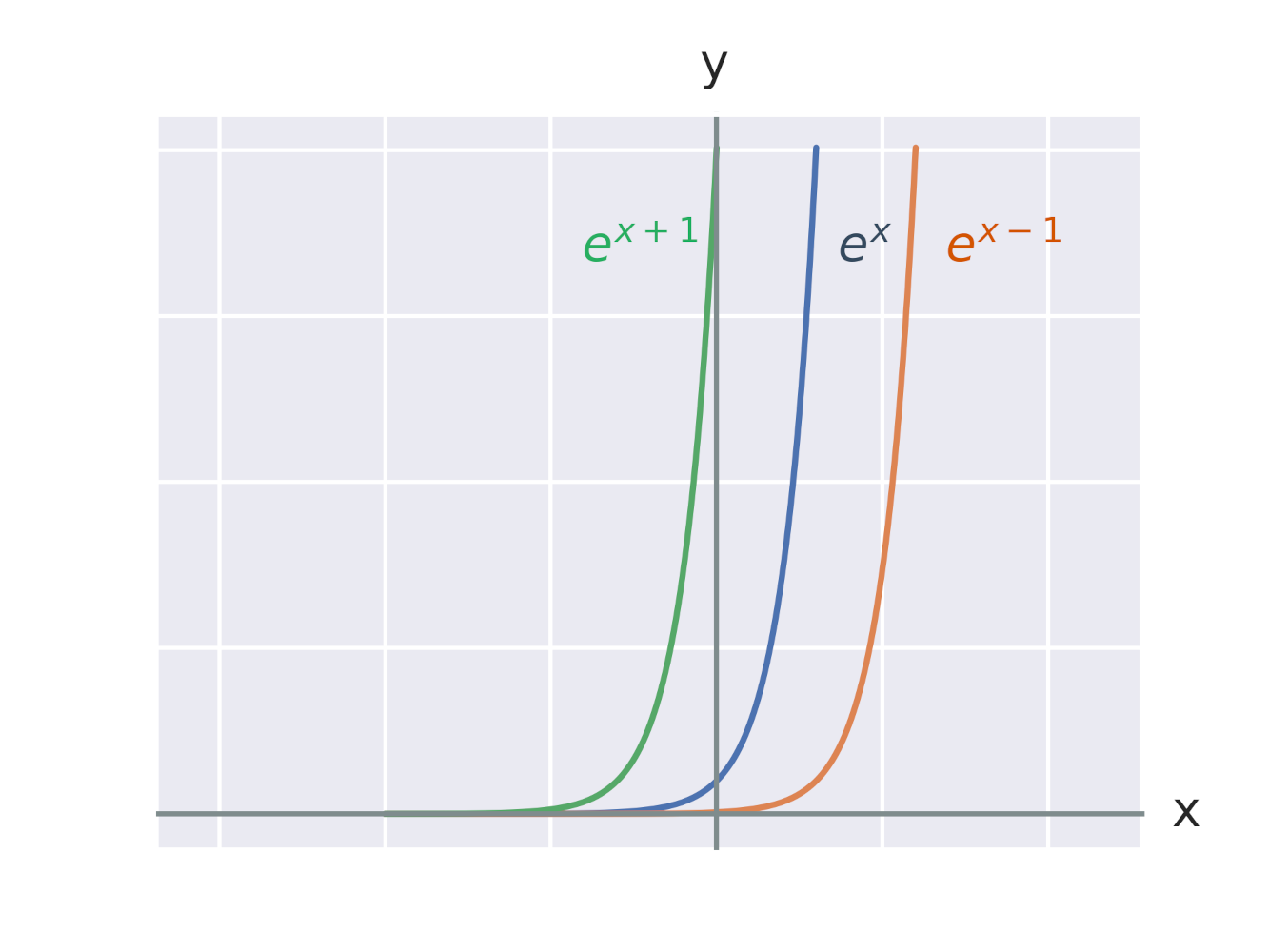
Efekt pripočítania konštanty k exponentu
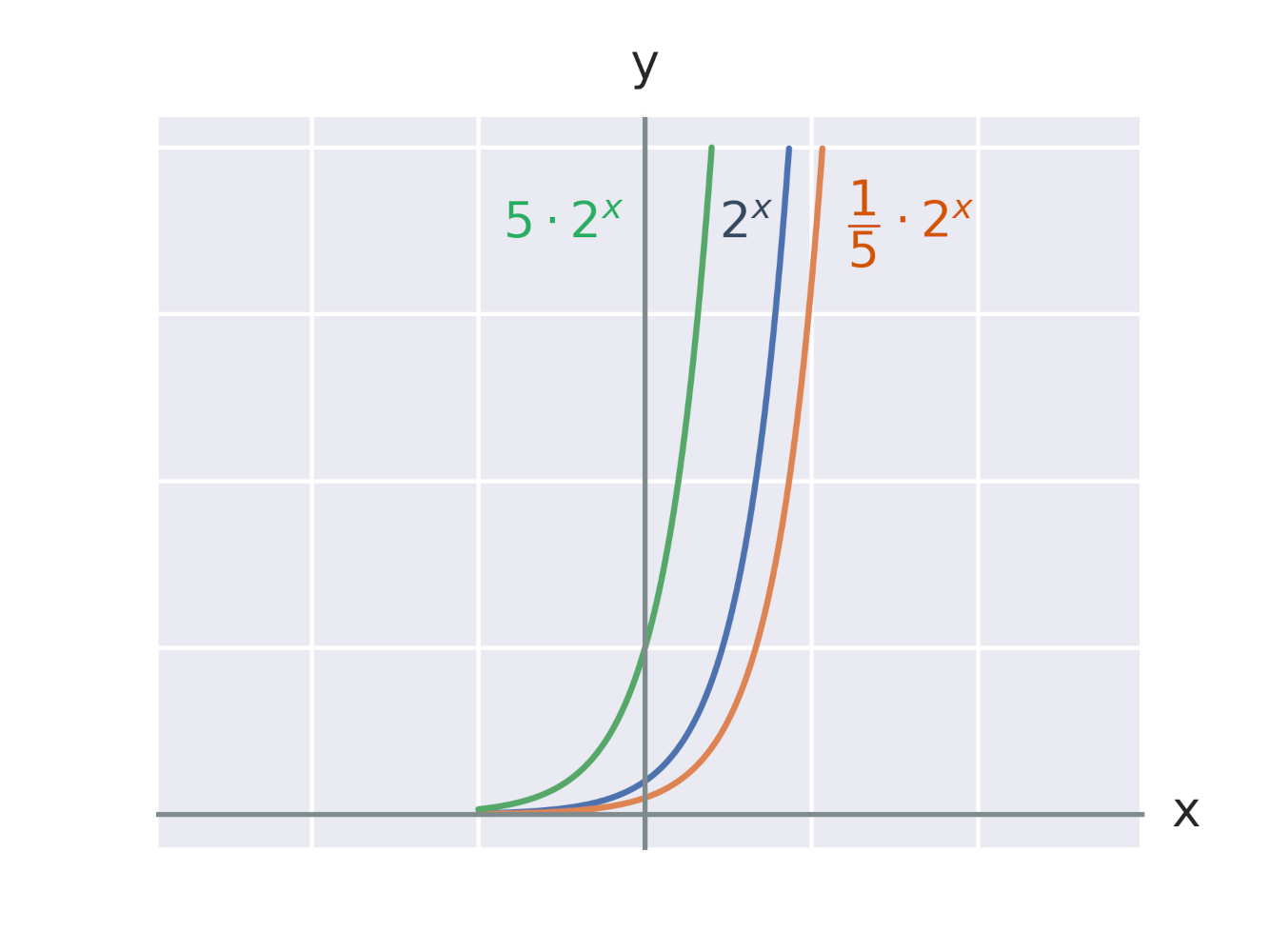
Efekt vynásobenia exponenciálnej funkcie konštantou
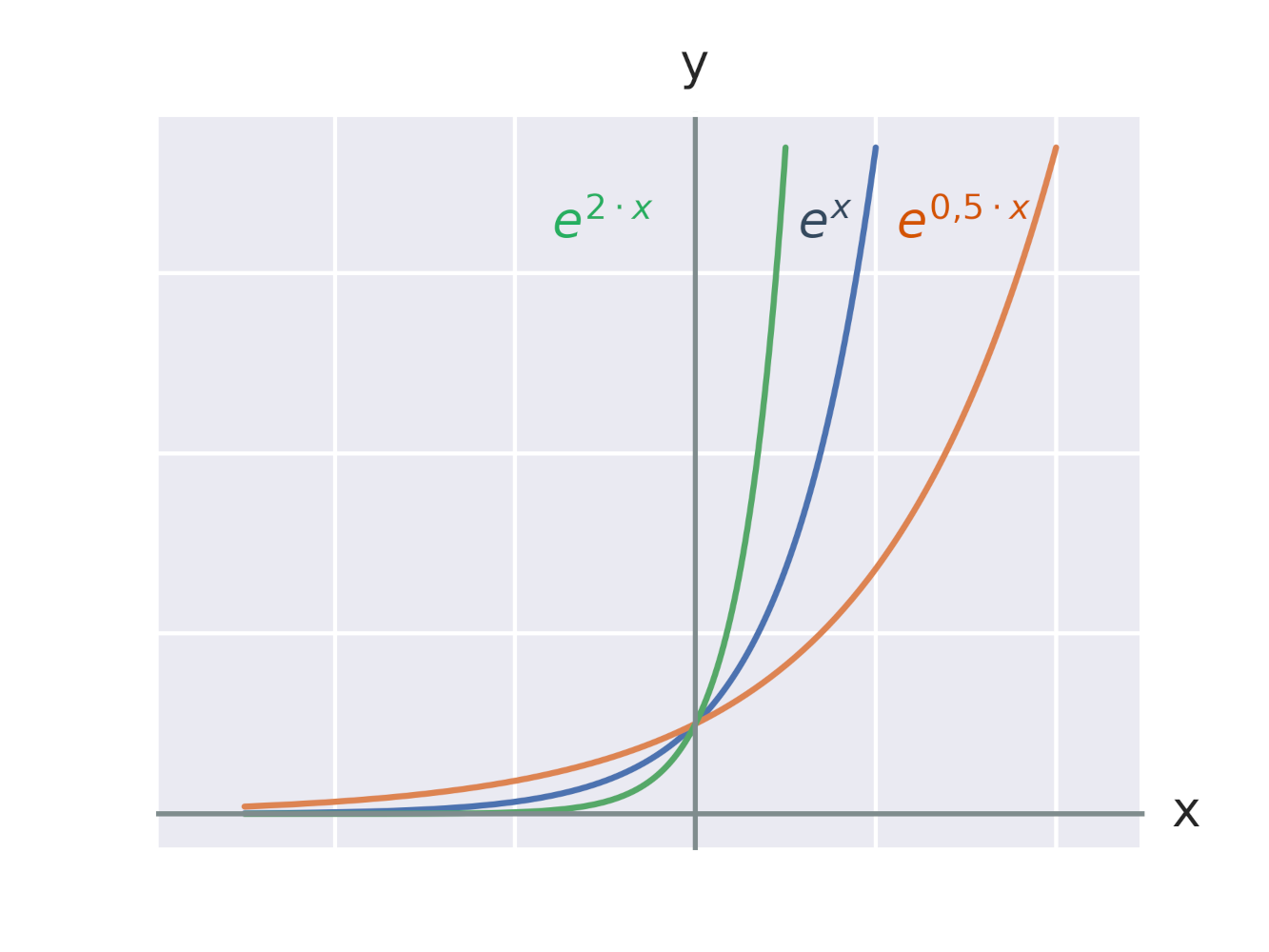
Efekt vynásobenia exponentu konštantou
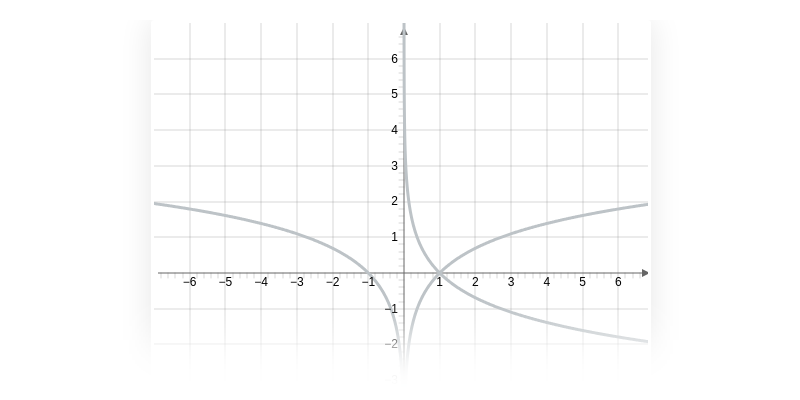
Grafy logaritmických funkcií
Logaritmická funkcia je inverzná k exponenciálnej funkcii s rovnakým základom. Grafy dvoch navzájom inverzných funkcií sú osovo súmerné podľa osi prvého kvadrantu (teda priamky spĺňajúcej x=y).
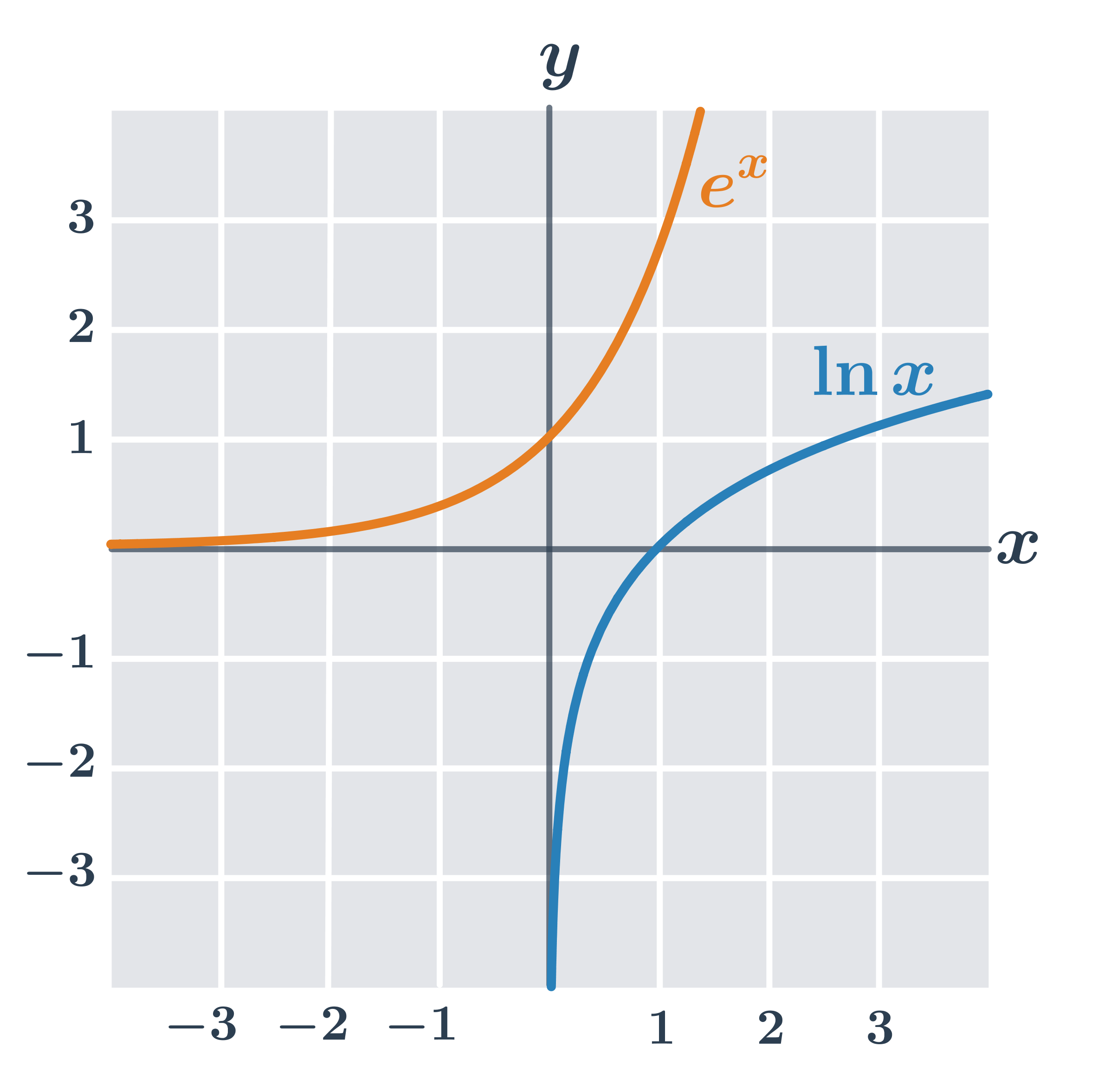
Na obrázku vidíme grafy logaritmických funkcií s rôznymi základmi 2, e, 10.
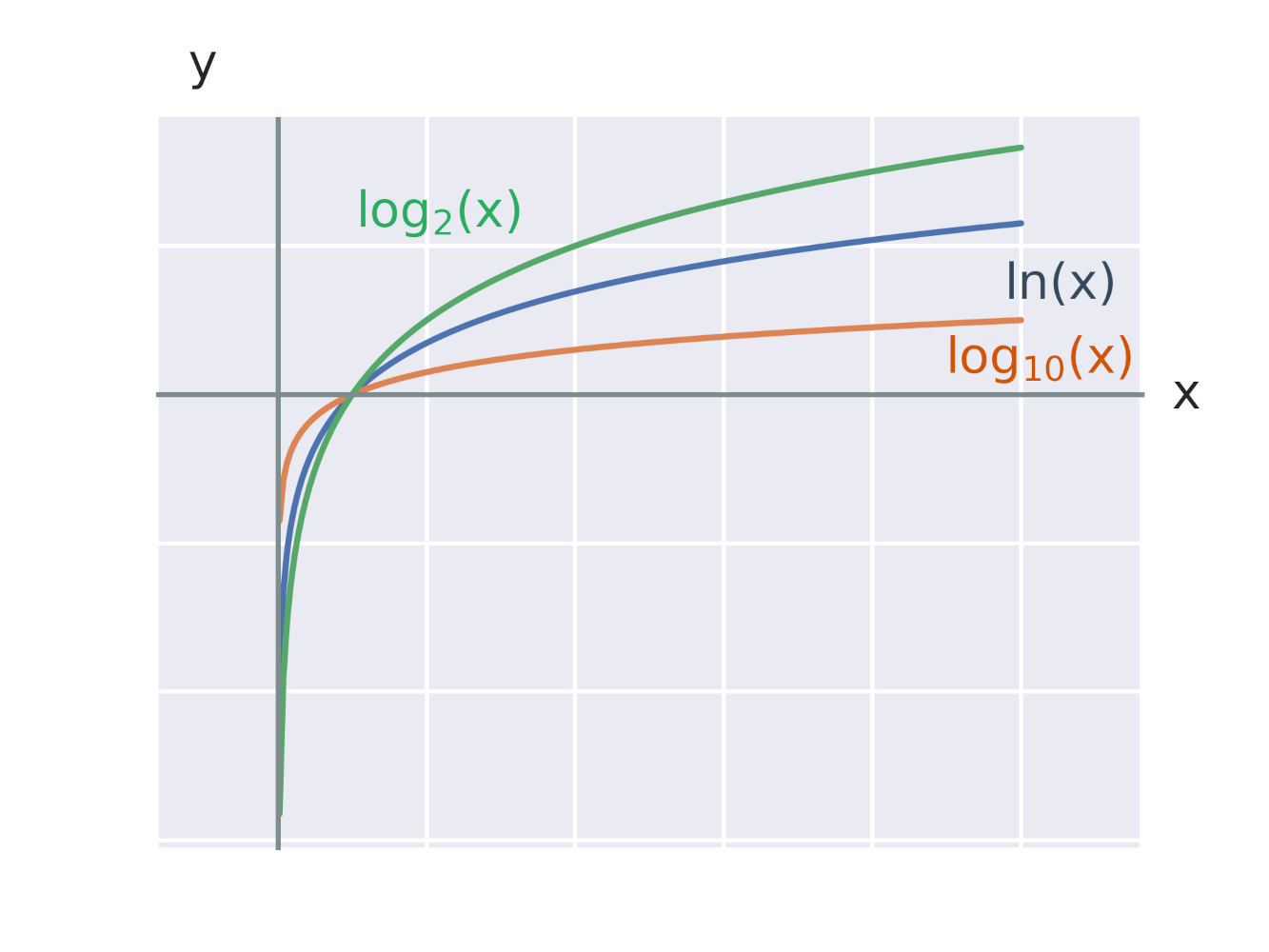
Značenie niektorých význačných logaritmických funkcií:
| funkcia | popis | značenie |
|---|---|---|
| \log_a x | všeobecne logaritmus x so základom a pre nejaké a >0, a\neq 1 | \log_a x |
| \log_e x | prirodzený logaritmus x | t u\ln x, v angl. textoch niekedy \log x |
| \log_{10} x | dekadický logaritmus x | tu \log x, v textoch slovenských aj angl. býva \log x, \log_{10}x |
| \log_2 x | binárny logaritmus x | tu \log_2 x, v textoch niekedy je aj \mathrm{lb}\;x |
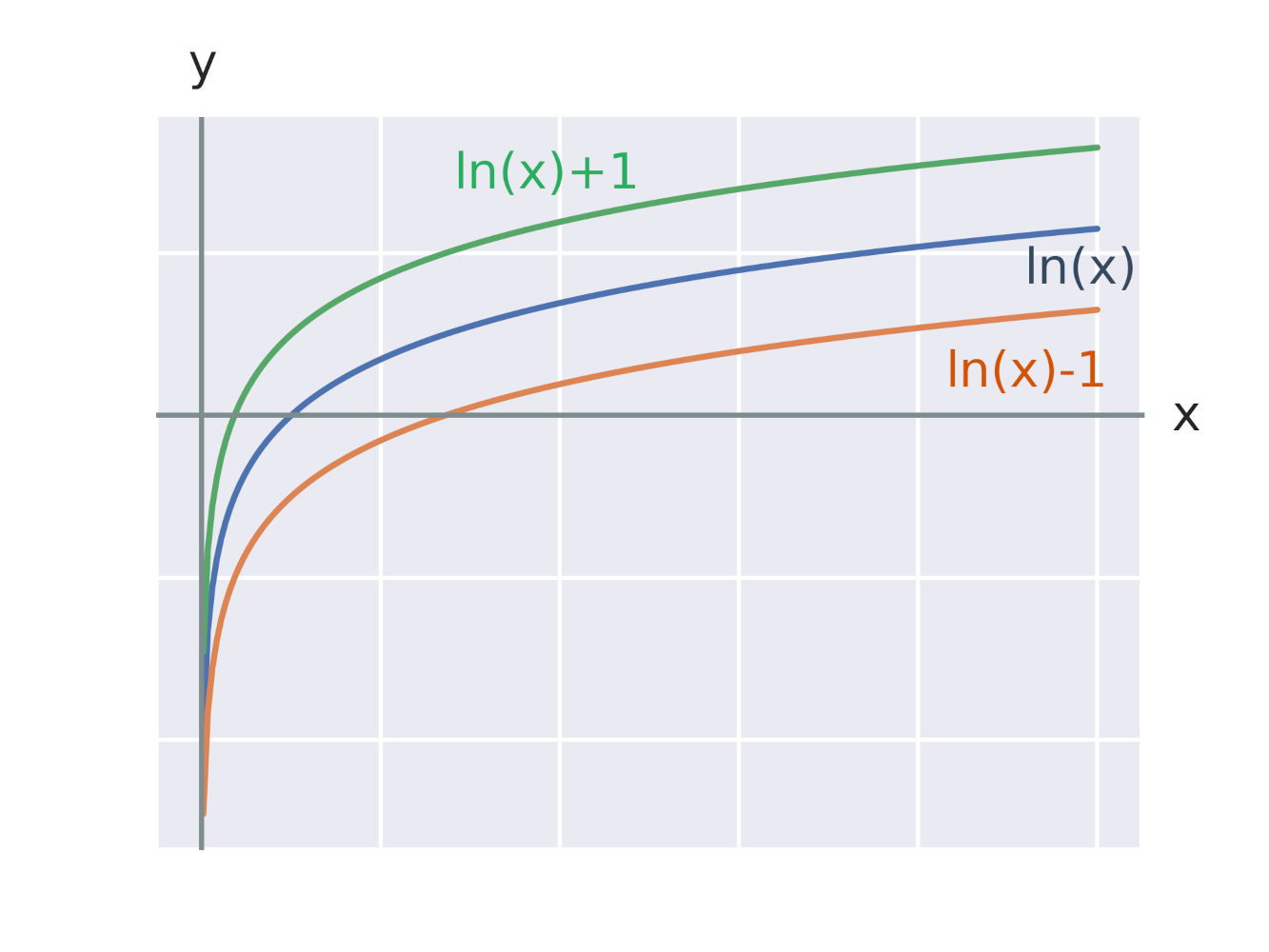
Efekt pripočítania konštanty k logaritmickej funkcii
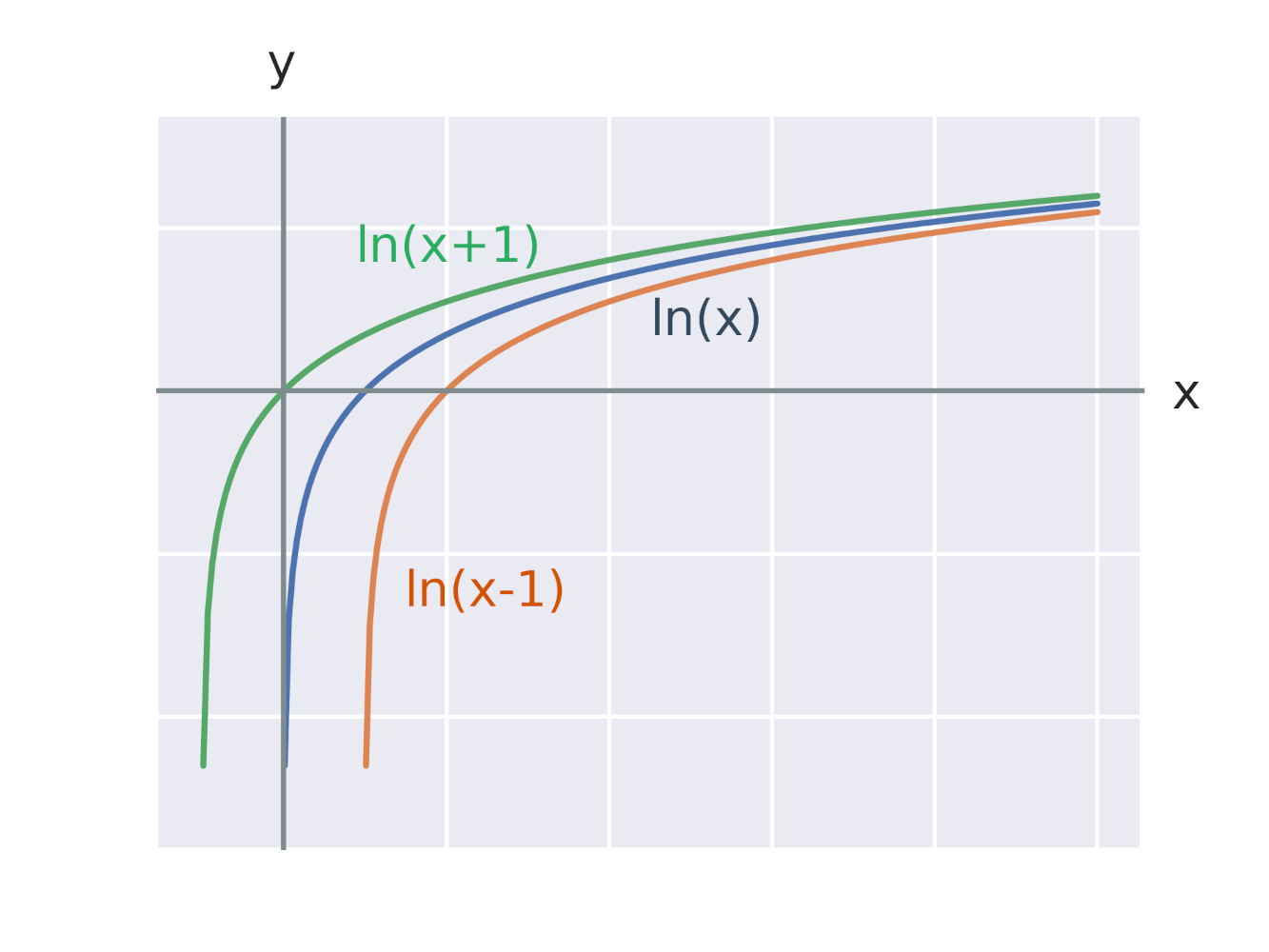
Efekt pripočítania konštanty k argumentu logaritmickej funkcie
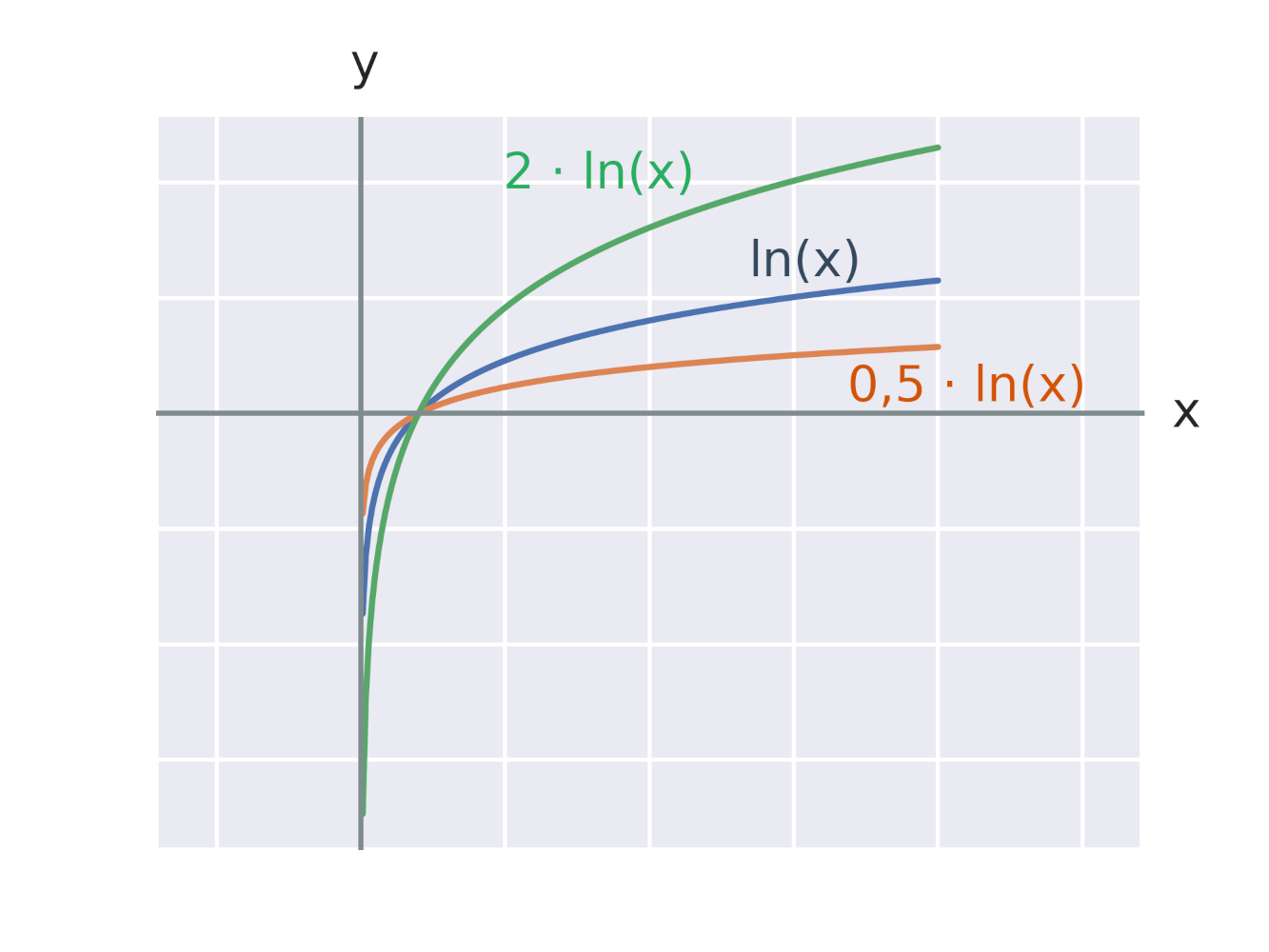
Efekt vynásobenia logaritmickej funkcie konštantou
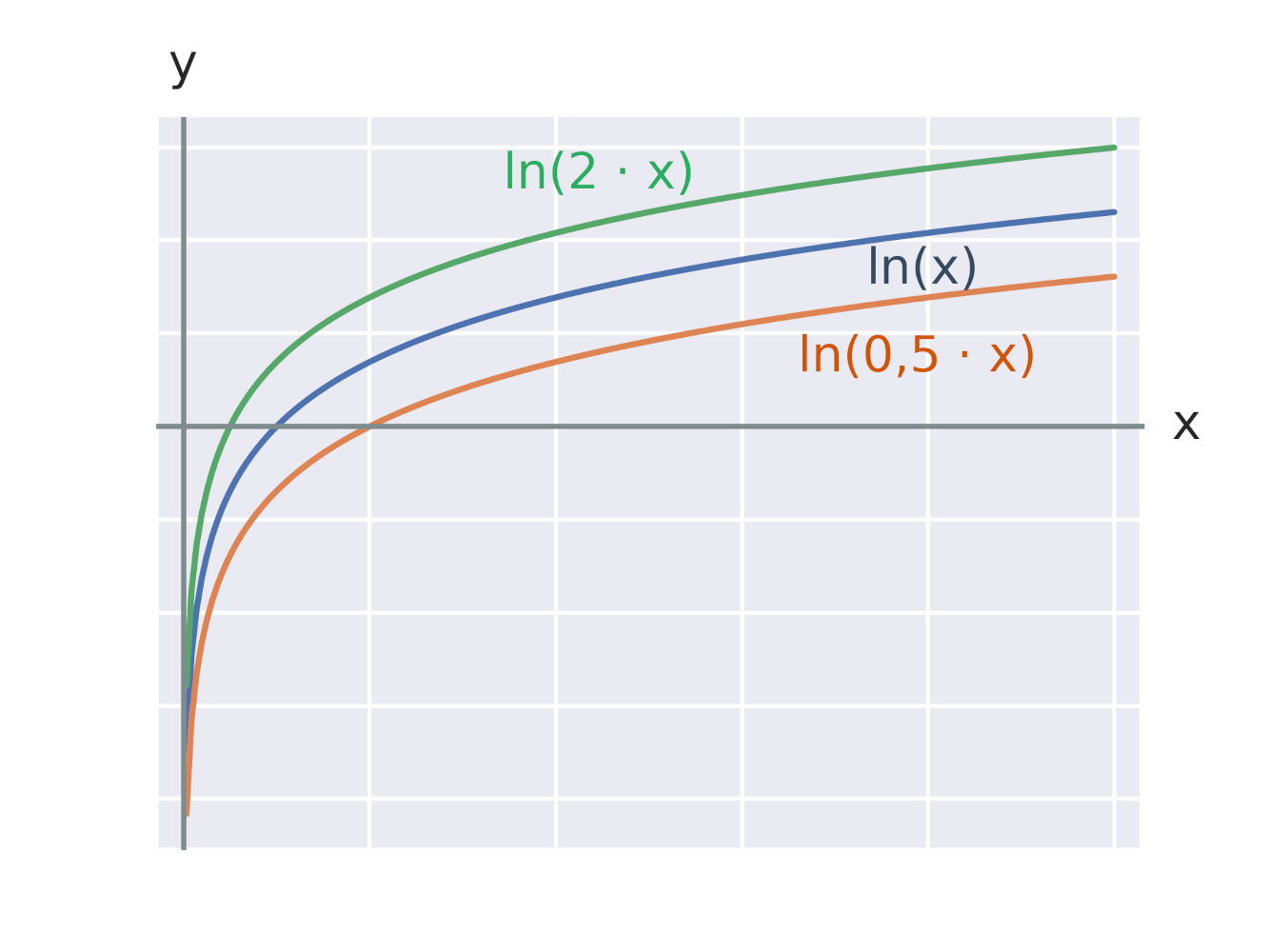
Efekt vynásobenie argumentu logaritmickej funkcie konštantou
Rozhodovačka
Rýchle precvičovanie výberom z dvoch možností.
Grafy exponenciálnych funkcií 
Zobraziť prehľad témy
ťažké
Grafy exponenciálnych funkcií (ťažké) • G1Z
Typicky zaberie: 5 min
Grafár
Špecializované cvičenie na prácu s grafom a funkciami.
Grafy exponenciálnych funkcií
Zobraziť prehľad témy
ťažké
Grafy exponenciálnych funkcií (ťažké) • E6S
Typicky zaberie: 8 min
Presúvanie
Presúvanie kartičiek na správne miesto. Jednoduché ovládanie, zaujímavé a neotrepané úlohy.
Grafy exponenciálnych funkcií
Zobraziť prehľad témy
Grafy exponenciálnych funkcií
ťažké
Grafy exponenciálnych funkcií (ťažké) • G7H
Typicky zaberie: 5 min
