Výpis prehľadov
Zlomky, percentá, desatinné čísla
Prechádzate súhrny informácií k určitým témam. Systémy Vieme sa zameriavajú hlavne na ich precvičovanie. K cvičeniam k jednotlivým podtémam sa dostanete pomocou odkazov nižšie.
Podkapitoly
- Zlomky, percentá, desatinné čísla
- Zlomky
- Zlomky: základy
- Určovanie zlomkov
- Zlomky na číselnej osi
- Porovnávanie zlomkov
- Zmiešané čísla
- Výpočty so zlomkami
- Krátenie zlomkov
- Sčítanie a odčítanie zlomkov
- Násobenie a delenie zlomkov
- Zlomky, mocniny, odmocniny
- Percentá
- Percentá: určovanie
- Počítanie s percentami
- Zlomky a percentá
- Desatinné čísla
- Desatinné čísla: základy
- Desatinné čísla slovom
- Porovnávanie desatinných čísel
- Zaokrúhľovanie desatinných čísel
- Desatinné čísla na číselnej osi
- Výpočty s desatinnými číslami
- Sčítanie a odčítanie desatinných čísel
- Násobenie desatinných čísel
- Delenie desatinných čísel
- Zlomky a desatinné čísla
Zlomky, percentá, desatinné čísla
Zlomky, percentá a desatinné čísla vyzerajú na prvý pohľad úplne inak, no úzko spolu súvisia – umožňujú nám vyjadrovať časti celku.
Napríklad ak je pohár z polovice plný vody, môžeme tento stav zapísať:
- zlomkom: \frac{1}{2},
- percentami: 50 %,
- desatinným číslom: 0,5.
Iný príklad – máme na obed pizzu a jednu štvrtinu sme už zjedli. Zostávajú nám teda tri štvrtiny, čo môžeme zapísať:
- zlomkom: \frac{3}{4},
- percentami: 75 %,
- desatinným číslom: 0,75.
Zlomky zapisujeme v tvare \frac{a}{b}, kde a sa nazýva čitateľ a b menovateľ. Aby mal zlomok zmysel, nesmie byť menovateľ nula. Význam zlomku zodpovedá deleniu. Napríklad: v zlomku \frac32 je čitateľom číslo 3 a menovateľom číslo 2, hodnota zlomku \frac32 sa rovná deleniu 3:2 = 1{,}5 („jeden a pol“).
Rozširovanie a krátenie
Hodnota zlomku sa nemení rozširovaním a krátením (nenulovým číslom c).
| Rozšírenie číslom c: | \frac{a}{b} = \frac{c\cdot a}{c \cdot b} |
| Krátenie číslom c: | \frac{a}{b} = \frac{a:c}{b:c} |
Príklady:
- Rozšírenie zlomku \frac64 číslom 5: \frac64 = \frac{6\cdot 5}{4\cdot 5} = \frac{30}{20}.
- Krátenie zlomku \frac64 číslom 2: \frac64 = \frac{6:2}{4:2} = \frac{3}{2}.
Základný tvar
Vďaka rozširovaniu a kráteniu môžeme rovnakú hodnotu zapísať nekonečným množstvom rôznych zlomkov. Zlomok \frac{a}{b} je v základnom tvare, ak sú čísla a, b nesúdeliteľné (ich jediný kladný spoločný deliteľ je teda číslo 1). Príklady:
- Zlomok \frac64 nie je v základnom tvare, pretože čísla 6 a 4 sú súdeliteľné (majú spoločný deliteľ 2, ktorým je možné zlomok krátiť).
- Zlomok \frac34 je v základnom tvare, pretože čísla 3 a 4 sú nesúdeliteľné.
Zlomky: základy
Zlomky zapisujeme v tvare \frac{a}{b}, kde a sa nazýva čitateľ a b menovateľ. Aby mal zlomok zmysel, nesmie byť menovateľ nula. Význam zlomku zodpovedá deleniu. Príklad: v zlomku \frac32 je čitateľom číslo 3 a menovateľom číslo 2, hodnota zlomku \frac32 sa rovná deleniu 3:2 = 1{,}5 („jedna a pol“).
Zlomok \frac{a}{b} je v základnom tvare, ak sú čísla a, b nesúdeliteľné (teda ich jediný kladný spoločný deliteľ je číslo 1). Na základný tvar prevádzame zlomky pomocou krátenia. Príklady:
- Zlomok \frac64 nie je v základnom tvare, pretože čísla 6 a 4 sú súdeliteľné – majú spoločný deliteľ 2, ktorým je možné zlomok krátiť, čím dostávame základný tvar \frac32.
- Zlomok \frac34 je v základnom tvare, pretože čísla 3 a 4 sú nesúdeliteľné.
Základy práce so zlomkami si môžete precvičiť v týchto témach:
HoreUrčovanie zlomkov
Zlomky vyjadrujú „časti z celku“. Môžeme ich graficky vyjadriť mnohými spôsobmi:

Zlomky na číselnej osi
Zlomok môžeme na číselnú os umiestniť tak, že ho prevedieme na desatinné číslo (vydelíme jednoducho čitateľ menovateľom) a potom postupujeme rovnako ako pri desatinných číslach. Napríklad \frac{6}{5} = 1{,}2, teda zlomok \frac{6}{5} leží dve desatiny za jednotkou. Ďalšie príklady:
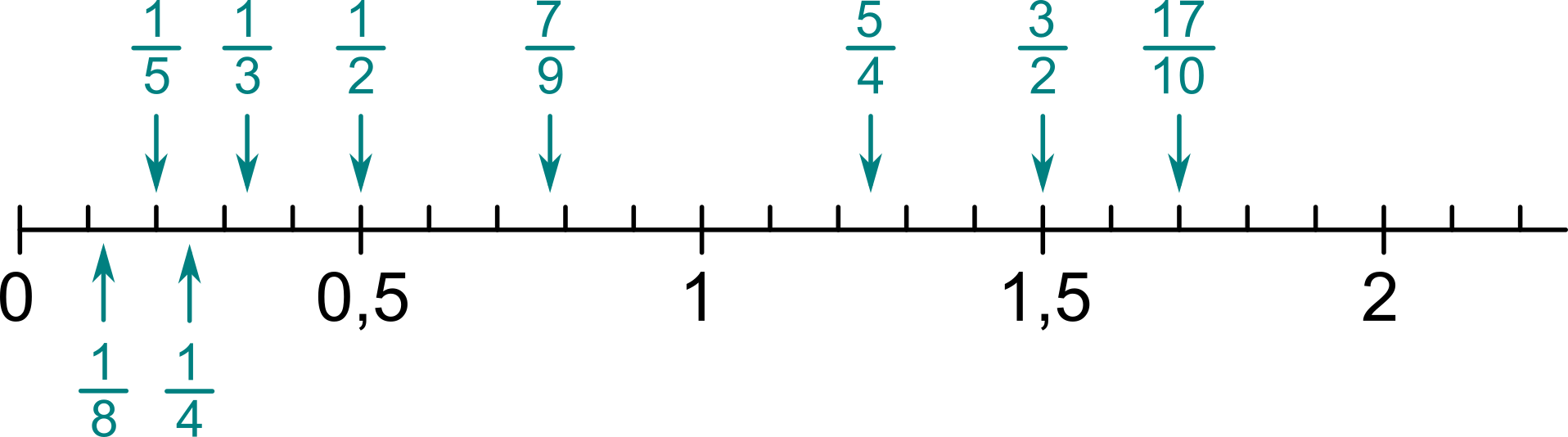
Zlomky menšie než 1 môžeme umiestňovať na číselnú os tiež priamo (bez prevodu na desatinné číslo) vďaka predstave „časť z celku“. Ak máme umiestniť zlomok \frac{3}{7}, predstavíme si, ako by sme rozdelili úsečku od 0 po 1 na sedem rovnakých častí. Zlomok \frac{3}{7} potom umiestnime na tretiu pozíciu.
Hodí sa si vybudovať dobrú predstavu hlavne pre zlomky s malým menovateľom:
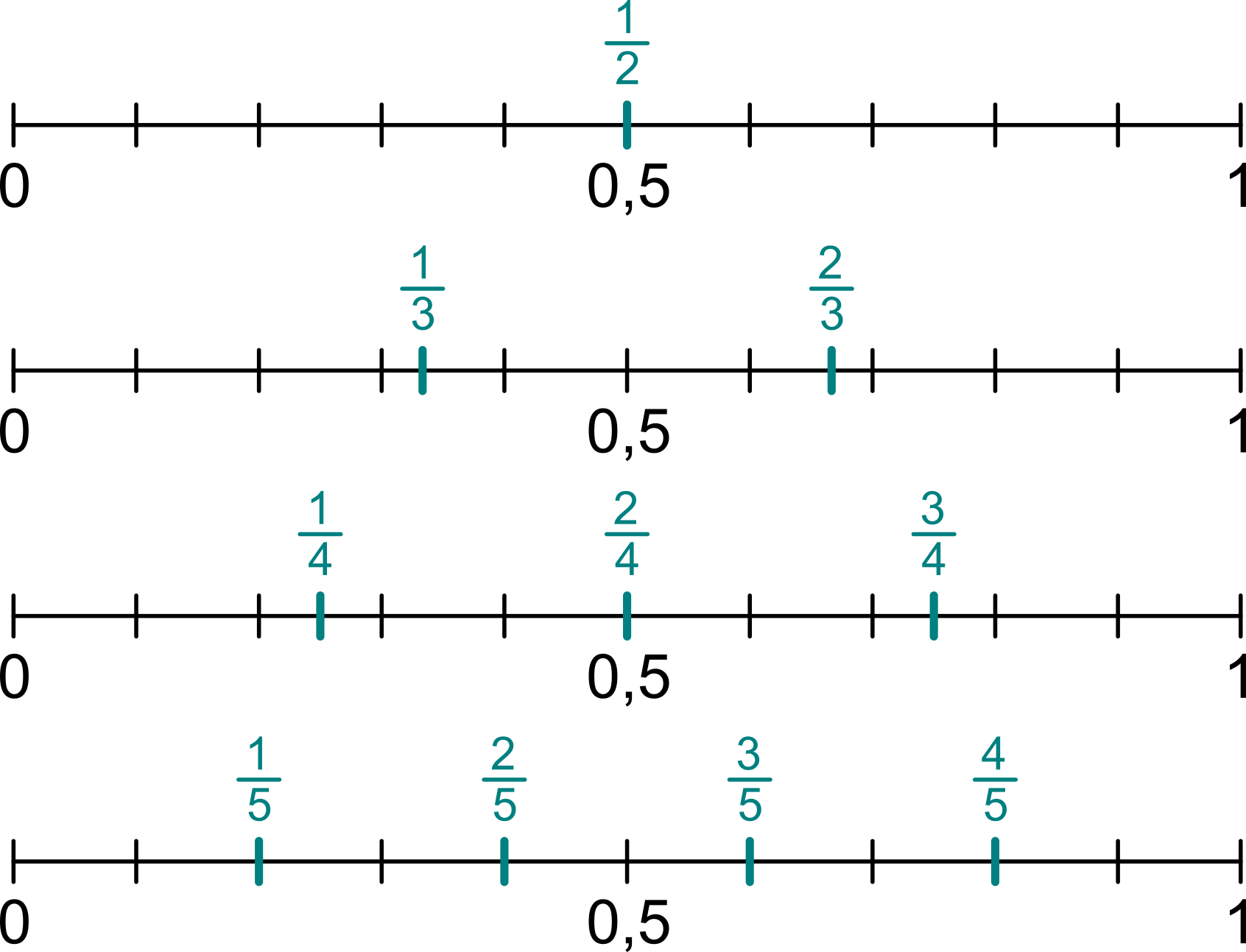
Porovnávanie zlomkov
Než sa pustíme do porovnávania zlomkov, je dobré mať jasno v tom, čo je čitateľ („to hore“) a menovateľ („to dole“). V zlomku \frac{3}{7} je 3 čitateľ, 7 menovateľ.
Porovnávanie zlomkov s rovnakým menovateľom
Porovnávania zlomkov s rovnakým menovateľom je jednoduché: stačí jednoducho porovnať čitatele. Ak napríklad porovnávame zlomky \frac{3}{7} a \frac{5}{7}, je väčší druhý zlomok. Oba zlomky vyjadrujú sedminy z celku a je jednoducho viac, keď máme sedmín päť.
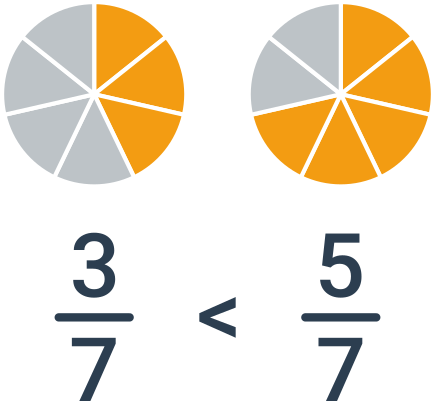
Porovnávanie zlomkov s rovnakým čitateľom
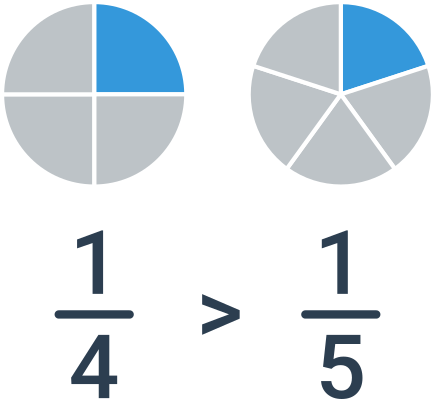
Ak majú zlomky rovnaký čitateľ, potom stačí porovnať menovatele. V tomto prípade je ale poradie zlomkov opačné než poradie menovateľov. Ak porovnávame napríklad zlomky \frac{1}{4} a \frac{1}{5}, je väčšia jedna štvrtina: dostanem väčší kúsok pizzy, ak sa bude deliť medzi 4 ľudí, než keď sa bude deliť medzi 5 ľudí.
Odlišný menovateľ aj čitateľ
V tomto prípade potrebujeme zlomky najskôr previesť na spoločný menovateľ a až potom vykonať porovnanie podľa čitateľov. Príklad: porovnanie zlomkov \frac{2}{3} a \frac{4}{7}. Najmenší spoločný menovateľ je 21, po rozšírení dostávame dvojicu zlomkov \frac{2}{3}=\frac{2\cdot 7}{3\cdot 7}=\frac{14}{21} a \frac{4}{7}=\frac{4\cdot 3}{7\cdot 3}=\frac{12}{21}. Pretože 14 > 12, je väčší prvý zlomok, tj. \frac{2}{3}.
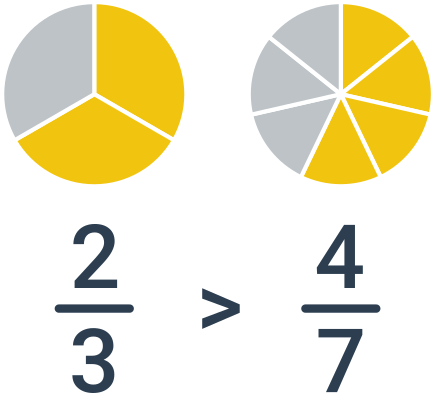
Porovnanie bez výpočtu
Často môžeme vykonať porovnanie aj bez detailného výpočtu, ak si zlomky správne predstavíme alebo porovnáme s vhodnou hodnotou „medzi“:
Zlomky \frac{2}{3} a \frac{7}{6}. Prvý z nich je menší než 1, druhý je väčší než 1. Platí teda \frac{2}{3} < \frac{7}{6}.
Zlomky \frac{1}{3} a \frac{4}{5}. Prvý z nich je určite menší než polovica, druhý je výrazne väčší než polovica. Platí teda \frac{1}{3} < \frac{4}{5}.
Zmiešané čísla
Ak má zlomok menovateľ väčší než čitateľ (zlomok je menší než jedna), označuje sa zlomok ako pravý. Nepravé zlomky (teda tie, ktoré sú väčšie ako jedna) môžeme zapísať pomocou zmiešaného čísla. Zmiešané číslo a\frac{b}{c} je zápis súčtu a + \frac{b}{c}, kde \frac{b}{c} je kladný zlomok menší než jedna. Príklady:
- 1\frac{1}{2} = \frac{3}{2}
- 2\frac{3}{5} = \frac{13}{5}
Prevod zmiešaného čísla na zlomok urobíme na základe pozorovania, že jednotku môžeme zapísať ako \frac{c}{c}. Príklad: 3\frac14 = 3\cdot\frac44 + \frac14 = \frac{12}{4}+\frac14 = \frac{13}{4}.

Prevod nepravého zlomku na zmiešané číslo urobíme pomocou delenia so zvyškom. Celá časť zmiešaného čísla zodpovedá podielu, čitateľ zvyšného zlomku zodpovedá zvyšku. Príklad:
- \frac{17}{3} = 5\frac23, pretože 17:3 je 5 a zvyšok 2.
- \frac{15}{7}= 2\frac17, pretože 15:7 je 2 a zvyšok 1.
Výpočty so zlomkami
Základné výpočty so zlomkami sú nasledujúce:
- Zlomky sa krátia tak, že čitateľ aj menovateľ vydelíme ich spoločným deliteľom.
- Zlomok \frac{9}{12} môžeme skrátiť na \frac{3}{4}, pretože čitateľ aj menovateľ majú spoločný deliteľ 3.
- Pre sčítanie a odčítanie zlomkov je nutné previesť zlomky na spoločný menovateľ.
- \frac{1}{4} + \frac{1}{6} prevedieme na spoločný menovateľ 12 a dostaneme \frac{3}{12} + \frac{2}{12} = \frac{5}{12}.
- Násobenie sa vykonáva tak, že vynásobíme čitateľ aj menovateľ medzi sebou.
- \frac{2}{3} \cdot \frac{3}{4} = \frac{6}{12} = \frac{1}{2}
- Delenie sa vykonáva násobením prevráteného zlomku.
- \frac{2}{3} : \frac{3}{4} = \frac{2}{3} \cdot \frac{4}{3} = \frac{8}{9}
- Prevod zlomku na percentá sa vykonáva pomocou násobenia 100.
- \frac{3}{4} = 0{,}75 = 75 \%
- Zlomky prevedieme na desatinné čísla tak, že čitateľ vydelíme menovateľom. Naopak desatinné číslo je možné previesť na zlomok pomocou roznásobenie mocninami desiatky.
- \frac{2}{5} = 2 : 5 = 0{,}4
- 0{,}25 = 0{,}25 \cdot\frac{100}{100} = \frac{25}{100}, čo po skrátení dáva \frac{1}{4}
Kombinácie operácií so zlomkami
- Zadania kombinujúce rôzne aritmetické operácie so zlomkami.
Krátenie zlomkov
Rovnakú hodnotu môžeme vyjadriť mnohými zlomkami, napríklad \frac23 = \frac46 = \frac{10}{15} = \frac{200}{300}. Len jedno možné vyjadrenie však považujeme za základný tvar. Zlomok je v základnom tvare, ak sú čitateľ a menovateľ nesúdeliteľné, nemajú teda žiadny spoločný deliteľ okrem jednotky. V uvedenom príklade je v základnom tvare zlomok \frac23.
Ako krátenie zlomku sa označuje operácia, kedy čitateľ a menovateľ vydelíme rovnakým, nenulovým číslom. Krátenie zachováva hodnotu zlomku. Ak chceme zlomok previesť do základného tvaru, krátime najväčším spoločným deliteľom čitateľa a menovateľa.
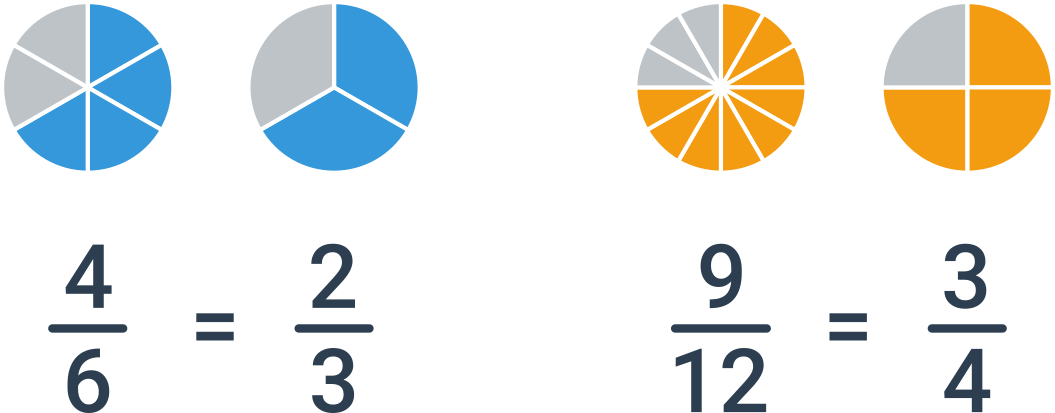
Príklady
Zlomok \frac{15}{28} je v základnom tvare, pretože čísla 15 a 28 nemajú spoločný deliteľ (sú nesúdeliteľné).
Zlomok \frac{25}{30} môžeme krátiť číslom 5, čím dostaneme zlomok \frac{5}{6}, ktorý je v základnom tvare.
Zlomok \frac{12}{18} môžeme krátiť číslom 2, čím dostaneme zlomok \frac{6}{9}. Ak chceme krátiť na základný tvar, nájdeme najväčší spoločný deliteľ čísel 12 a 18, čo je 6. Po krátení číslom 6 dostávame zlomok \frac{2}{3}.
Sčítanie a odčítanie zlomkov
Než sa pustíme do sčítania zlomkov, je dobré mať jasno v tom, čo je čitateľ („to hore“) a menovateľ („to dole“). V zlomku \frac{3}{7} je 3 čitateľ, 7 menovateľ.
Sčítanie zlomkov s rovnakým menovateľom
Ak majú sčítané zlomky rovnaké menovatele, stačí jednoducho sčítať čitatele. Menovateľ necháme rovnaký, teda \frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}.
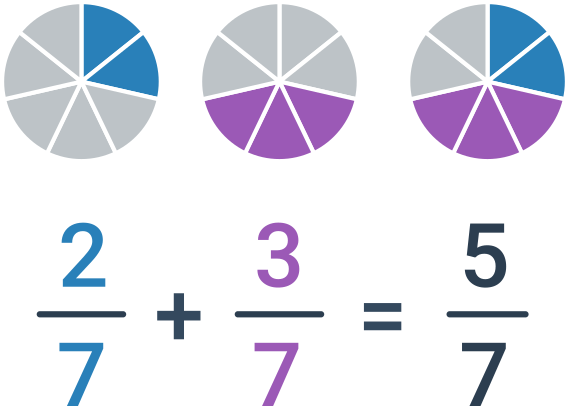
Sčítanie zlomkov s rôznymi menovateľmi
Ak majú sčítané zlomky rôzne menovatele, musíme ich najskôr rozšíriť tak, aby mali rovnaký menovateľ. Najvýhodnejšie je rozšíriť zlomky na najmenší spoločný násobok pôvodných menovateľov. Keď už majú zlomky rovnaký menovateľ, sčítame ich vyššie uvedeným postupom.
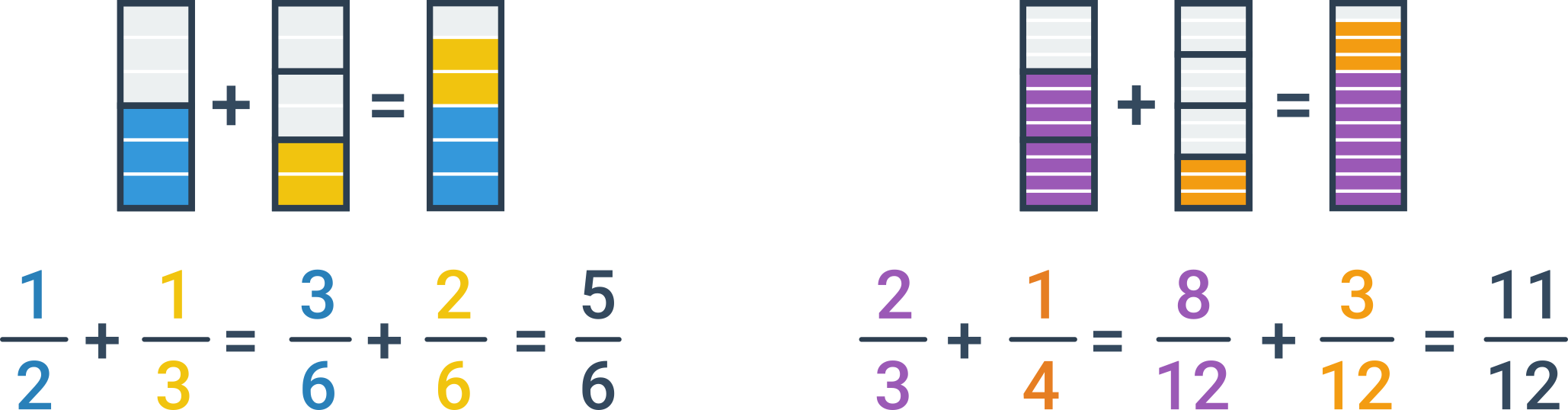
Úpravy a odčítanie
Výsledný zlomok väčšinou ešte krátime, aby sme dostali výsledok v základnom tvare. Odčítanie zlomkov funguje rovnakým spôsobom.
Príklady
Príklad s rovnakým menovateľom, bez nutnosti krátenia:
\frac{2}{5}+\frac{1}{5} = \frac{2+1}{5} = \frac{3}{5}.Príklad s rovnakým menovateľom, kedy výsledok krátime:
\frac{5}{6}-\frac{1}{6} = \frac{5-1}{6} = \frac{4}{6} = \frac{2}{3}.Príklad s rôznymi menovateľmi: \frac{5}{6} - \frac{3}{4}. Najmenší spoločný násobok menovateľov 6 a 4 je 12, rozšírime teda zlomky na menovateľ 12:
\frac{5}{6} - \frac{3}{4} = \frac{5\cdot 2}{6\cdot 2} - \frac{3\cdot 3}{4\cdot 3}= \frac{10}{12} - \frac{9}{12} = \frac{1}{12}
Násobenie a delenie zlomkov
Násobenie zlomkov si môžeme predstaviť s pomocou čokolády. Ak násobíme \frac45\cdot \frac23 je to ako keby sme brali štyri z piatich stĺpčekov a dva z troch riadkov. Koľko štvorčekov čokolády takto vezmeme? Osem z pätnástich, teda \frac{8}{15}.

Pri násobení zlomkov teda jednoducho vynásobíme čitateľ prvého zlomku a čitateľ druhého zlomku a dostaneme výsledný čitateľ, podobne pre menovateľ: \frac{a}{b}\cdot \frac{c}{d} = \frac{a\cdot c}{b\cdot d}. Ak sa chceme vyhnúť násobeniu veľkých čísel, môžeme zlomky krátiť, a to aj „do kríža“. Príklady:
- \frac{2}{3}\cdot\frac{1}{5} = \frac{2\cdot 1}{3\cdot 5}=\frac{2}{15}
- \frac{2}{3}\cdot\frac{3}{4} = \frac{2\cdot 3}{3\cdot 4}=\frac{2}{4}=\frac{1}{2} (všimnite si, že neroznásobujeme, ale hneď krátime)
Delenie zlomkov je to isté ako násobenie prevráteným zlomkom: \frac{a}{b}:\frac{c}{d} = \frac{a}{b}\cdot\frac{d}{c}=\frac{a\cdot d}{b\cdot c}. Príklady:
- \frac13:\frac12 =\frac13\cdot \frac21 = \frac23
- \frac{2}{5}:\frac{3}{4}=\frac{2}{5}\cdot \frac{4}{3} = \frac{2\cdot 4}{5\cdot 3} = \frac{8}{15}
Zlomky, mocniny, odmocniny
Umocňovanie a odmocňovanie zlomkov
Pri umocňovaní (odmocňovaní) zlomku jednoducho umocníme (odmocníme) čitateľ aj menovateľ:
\large(\frac{2}{3}\large)^2 = \frac{2^2}{3^2} = \frac{4}{9}
\sqrt{\frac{2}{3}} = \frac{\sqrt{2}}{\sqrt{3}}
\large(\frac{4}{5}\large)^{-1} = \frac{4^{-1}}{5^{-1}} = \frac{5}{4} (umocňovanie na -1 zodpovedá zameneniu čitateľa a menovateľa)
Umocňovanie na zlomok
Umocňovanie na zlomok zodpovedá tomu, že vezmeme mocninu podľa čitateľa a odmocninu podľa menovateľa, teda x^\frac{a}{b} = \sqrt[b]{a^x}. Príklady:
2^\frac{2}{3} = \sqrt[3]{2^2} = \sqrt[3]{4} = 1{,}587\ldots
4^\frac{1}{2} = \sqrt{4^1} = 2
81^\frac{3}{4} = \sqrt[4]{81^3} = \sqrt[4]{81}^3 = 3^3 = 27
Percento (%) je bezrozmerová jednotka vyjadrujúca jednu stotinu celku. Napríklad zápis „42 %“ (42 percent) je to isté ako zlomok \frac{42}{100} alebo desatinné číslo 0,42.
Promile (‰) je jedna desatina percenta, teda jedna tisícina celku.
Základné využitie percent je na vyjadrenie časti celku, napríklad:
- aká časť obyvateľov pracuje v poľnohospodárstve,
- koľko študentov úspešne splnilo skúšku,
- koľko alkoholu obsahuje fľaša vína.
Ďalšie oblasti využitia percent sú:
- vyjadrovanie pravdepodobnosti (aká je šanca, že bude zajtra pršať),
- finančné vzťahy (zľavy, úroky),
- spracovanie a prezentovanie štatistických dát.
Percentá: určovanie
Pre dobré pochopenie percent je vhodné vybudovať si základný prehľad o tom, čo percentá znamenajú a ako zodpovedajú jednotlivé hodnoty grafickému znázorneniu. Pre niektoré často sa vyskytujúce hodnoty je dobrý nápad si ich význam zapamätať:
| 10 % | = | jedna desatina |
| 20 % | = | jedna pätina |
| 25 % | = | jedna štvrtina |
| 33 % | = | jedna tretina |
| 50 % | = | jedna polovica |
| 75 % | = | tri štvrtiny |
| 80 % | = | štyri pätiny = celok bez jednej pätiny |
| 90 % | = | deväť desatín = celok bez jednej desatiny |
Počítanie s percentami
Pre počítanie s percentami je najdôležitejšie si uvedomiť, že percento je jedna stotina, teda \frac{1}{100}. Ak teda chceme vypočítať napríklad „15 % z 300“, počítame takto: 15\ \% \textrm{ z } 300 = \frac{15}{100} \cdot 300 = 15 \cdot 3 = 45.
Pre niektoré často sa vyskytujúce percentá si môžeme výpočet uľahčiť:
50 % = jedna polovica, delíme teda číslom 2
25 % = jedna štvrtina, delíme teda číslom 4
10 % = jedna desatina, delíme teda číslom 10
90 % = bez jednej desatiny
Zlomky a percentá
Prevod percent na zlomok v základnom tvare
Jedno percento je to isté ako jedna stotina, teda \frac{1}{100}. Vynásobíme teda číslo (udávajúce percentá) zlomkom \frac{1}{100} a následne zlomok vykrátime (pomocou delenia najväčším spoločným deliteľom) na základný tvar. Príklady:
- 45\ \% = 45 \cdot \frac{1}{100} = \frac{45}{100} = \frac{5\cdot 9}{5\cdot 20}= \frac{9}{20}
- 12\ \% = 12 \cdot \frac{1}{100} = \frac{12}{100} = \frac{4\cdot 3}{4\cdot 25}= \frac{3}{25}
Prevod zlomku na percentá
Chceme zlomok \frac{a}{b} vyjadriť ako p\ \%. Pretože jedno percento je jedna stotina, musí teda platiť \frac{a}{b} = \frac{p}{100}. Takže p = \frac{a}{b}\cdot 100. Stačí teda zlomok vynásobiť číslom 100. Príklady:
- \frac{2}{5} = \frac{2}{5} \cdot 100\ \% = \frac{200}{5}\ \% = 40\ \%
- \frac{3}{20} = \frac{3}{20} \cdot 100\ \% = \frac{300}{20}\ \% = 15\ \%
Desatinné čísla
Desatinné číslo je spôsob zápisu čísla pomocou celej časti a desatinnej časti, ktorá je oddelená desatinnou čiarkou. Napríklad v zápise 154,28 je 154 celá časť a 28 desatinná časť. Na prvom mieste za desatinou čiarkou sú desatiny, na druhom stotiny, na treťom tisíciny.
Pomocou desatinných čísel vyjadrujeme čísla, ktoré nie sú „celé“. Napríklad ak rozdelíme 6 koláčov spravodlivo medzi 4 deti, dostane každé dieťa „jeden a pol“ koláča, čo zapisujeme ako 1,5.
Poznámka k zápisu desatinných čísel: v slovenčine sa používa desatinná čiarka. V anglofónnom svete sa používa desatinná bodka, namiesto 154,28 sa teda píše 154.28. Tento spôsob zápisu sa používa vo výpočtovej technike po celom svete.
HoreDesatinné čísla: základy
Pomocou desatinných čísel vyjadrujeme čísla, ktoré nie sú „celé“. Príklad: Ak rozdelíme 6 koláčov spravodlivo medzi 4 deti, dostane každé dieťa „jeden a pol“ koláča, čo zapisujeme ako 1,5.
Táto téma sa zaoberá základným porozumením desatinným číslam:
- Desatinné čísla slovom – prevod medzi slovným pomenovaním a číselným zápisom
- Porovnávanie desatinných čísel – porovnávanie kladných aj záporných čísel s desatinnou časťou
- Zaokrúhľovanie desatinných čísel – zaokrúhľovanie čísel na rôzne počty desatinných miest
- Desatinné čísla na číselnej osi – dobrá predstava o umiestnení čísel na číselnú os pomáha aj s inými operáciami (napr. zaokrúhľovanie a porovnanie)
Nadväzujúca téma potom rieši výpočty s desatinnými číslami.
HoreDesatinné čísla slovom
Desatinné čísla môžeme čítať mnohými rôznymi spôsobmi. Prvým je „priamočaré čítanie“, kedy namiesto „čiarka“ hovoríme „celé“. Desatinnú časť môžeme prečítať ako jedno číslo, alebo vymenovať po cifrách:
| 4,23 | = | „čtyri celé dvadsať tri“ |
| 21,508 | = | „dvadsaťjeden celé päť nula osem“ |
Ďalej môžeme desatinné číslo prečítať pomocou desatín, stotín, tisícin:
| 0,1 | = | „jedna desatina“ |
| 0,01 | = | „jedna stotina“ |
| 0,001 | = | „jedna tisícina“ |
| 3,4 | = | „tri a štyri desatiny“ |
| 0,25 | = | „dve desatiny a päť stotín“ = „dvadsaťpäť stotín“ |
| 42,007 | = | „štyridsaťdva a sedem tisícin“ |
Niekedy môžeme tiež desatinné číslo pomenovať podľa zlomku, ktorý predstavuje:
| 0,5 | = | „jedna polovica“ |
| 3,5 | = | „tri a pol“ |
| 0,25 | = | „jedna štvrtina“ |
Porovnávanie desatinných čísel
Pri porovnávaní desatinných čísel nájdeme tú „najdôležitejšiu“ časť v ktorej sú rozdielne a podľa nej porovnávame. Najskôr teda porovnávame celú časť. Ak sú celé časti zhodné, porovnávame desatiny, následne stotiny, tisíciny a tak ďalej. Nesmieme tiež zabudnúť skontrolovať znamienko, ktoré má rovnaký vplyv ako v prípade celých čísel. Príklady:
15{,}3 \lt 17{,}9987 – líši sa celá časť, takže pre účely porovnania môžeme desatinné miesta úplne ignorovať.
0{,}2 > 0{,}17 – celá časť je rovnaká, rozhodujeme teda podľa desatín, kde 2>1. Pri príkladoch tohto typu sa často robia chyby, pretože to vyzerá, že 17 > 2, čo je však chybná úvaha. Pre lepšiu predstavu si môžeme doplniť z pravej strany nulu: 0{,}20 > 0{,}17.
3{,}21 > -3{,}22 – tu vôbec nehrajú rolu desatinné miesta, pretože prvé číslo je kladné a druhé záporné.
-4{,}2791 \lt -4{,}2758 – porovnávanie vykonávame podľa cifier na pozícii tisícin (9 a 5), výsledok je „naopak“, pretože ide o záporné čísla.
Zaokrúhľovanie desatinných čísel
Zaokrúhľovanie desatinných čísel funguje podobne ako zaokrúhľovanie celých čísel, pracujeme však aj s časťou za desatinnou čiarkou. Pri desatinných číslach je téma zaokrúhľovania obzvlášť dôležitá, pretože sa jej občas nemôžeme vyhnúť – niektoré čísla v desiatkovej sústave totiž nie je možné presne zapísať, napríklad \frac{1}{3} = 0{,}3333\ldots, \sqrt{2} = 1{,}4142\ldots, \pi = 3{,}14 159\ldots
Zaokrúhľovanie na desatiny znamená, že číslo nahradíme najbližším násobkom čísla 0,1 (teda číslom s jednou cifrou za desatinnou čiarkou). Zaokrúhľovanie na stotiny znamená, že číslo nahradíme najbližším násobkom čísla 0,01 (teda číslom s dvomi ciframi za desatinnou čiarkou). Podobne zaokrúhľujeme aj s vyššou presnosťou. Rovnako ako pri zaokrúhľovaní celých čísel aj pri desatinných číslach zaokrúhľujeme čísla končiace sa číslicou 5 nahor. Príklady:
3,628 zaokrúhlené na desatiny je 3,6.
3,628 zaokrúhlené na stotiny je 3,63.
12,25 zaokrúhlené na desatiny je 12,3.
4,8975 zaokrúhlené na celé číslo je 5.
84,15 zaokrúhlené na desiatky je 80 (pozor na rozdiel medzi zaokrúhľovaním na „desatiny“ a „desiatky“).
Desatinné čísla na číselnej osi
Podobne ako pri iných číselných osiach, prvý krok je určiť, aké sú rozostupy medzi značkami na číselnej osi. Pri práci s desatinnými číslami býva často rozostup 0,1 (jedna desatina), ale nemusí to tak byť vždy.
Príklad:

Výpočty s desatinnými číslami
Táto téma sa zaoberá aritmetickými operáciami s desatinnými číslami:
Sčítanie a odčítanie desatinných čísel
- Pri sčítaní a odčítaní desatinných čísel je dôležité zarovnať čísla podľa desatinnej čiarky.
- 3{,}75 + 1{,}2 = 4{,}95
- Pri násobení desatinných čísel násobíme rovnako ako celé čísla a potom správne umiestnime desatinnú čiarku v závislosti od počtu desatinných miest.
- 1{,}2 \times 3{,}4 = 4{,}08
- Pri delení desatinných čísel sa môžeme desatinnej časti zbaviť tak, že delenec aj deliteľ vynásobíme dostatočne veľkou mocninou desiatky. Následne potom čísla delíme rovnako ako prirodzené čísla.
- 4{,}5 : 1{,}5 = 45 : 15 = 3
- Zlomky prevedieme na desatinné čísla tak, že čitateľ vydelíme menovateľom. Naopak desatinné číslo je možné previesť na zlomok pomocou roznásobenia mocninami desiatky.
- \frac{2}{5} = 2 : 5 = 0{,}4
- 0{,}25 = 0{,}25 \cdot\frac{100}{100} = \frac{25}{100}, čo po vykrátení dáva \frac{1}{4}
Kombinácie operácií s desatinnými číslami
- Zadanie kombinujúce rôzne aritmetické operácie s desatinnými číslami.
Sčítanie a odčítanie desatinných čísel
Pri sčítaní a odčítaní desatinných čísel postupujeme rovnako ako pri bežnom sčítaní a odčítaní, čísla len musíme mať „zarovnané“ podľa desatinnej čiarky. Vhodnou pomôckou (hlavne pri sčítaní a odčítaní pod sebou) môže byť doplniť si nuly z pravej strany, aby mali obe čísla rovnaký počet cifier za desatinnou čiarkou. Príklady:
1{,}2+2{,}3 = 3{,}5
3{,}457+4{,}2 = 3{,}457+4{,}200 = 7{,}657
1{,}3-0{,}8 = 0{,}5
0{,}001+0{,}01+0{,}1 = 0{,}001+0{,}010+0{,}100 = 0{,}111
2{,}01-0{,}1 = 2{,}01 - 0{,}10 = 1{,}91
Násobenie desatinných čísel
Násobenie desatinných čísel môžeme vykonať nasledujúcim spôsobom: 1) Obe čísla vynásobíme, ako keby desatinnú čiarku vôbec nemali. 2) Do výsledku umiestnime desatinnú čiarku tak, aby mal výsledok toľko desatinných miest ako oba činitele spolu. Tento postup zodpovedá násobeniu a následnému deleniu mocninami desiatky. Príklady:
5 \cdot 0{,}4 – násobíme 5\cdot 4 = 20, výsledok posunieme o 0+1=1 desatinné miesto, dostávame 2{,}0.
2{,}5 \cdot 0{,}05 – násobíme 25\cdot 5=125, výsledok posunieme o 1+2=3 desatinné miesta, dostávame 0,125.
0{,}9 \cdot 0{,}8 – násobíme 9\cdot 8=72, výsledok posunieme o 1+1=2 desatinné miesta, dostávame 0,72.
Výsledok je dobré skontrolovať rýchlym odhadom pomocou zaokrúhlených čísel. Napríklad pri násobení 0{,}9 \cdot 0{,}8 sú oba činitele „trochu menšie než 1“, takže aj výsledok by mal byť „trochu menší než 1\cdot 1“, pri násobení 4{,}92\cdot 3{,}06 môžeme ľahko odhadnúť, že výsledok by mal byť približne 5\cdot 3=15.
HoreDelenie desatinných čísel
Pri delení desatinných čísel sa môžeme desatinnej časti ľahko zbaviť tak, že delenec aj deliteľ vynásobíme dostatočne veľkou mocninou desiatky. Následne potom čísla delíme rovnako ako prirodzené čísla. Príklady:
- 8:0{,}2 = 80:2 = 40
- 1:0{,}05 = 100:5 = 20
- 2{,}5:2 = 25:20 = 1{,}25
Zlomky a desatinné čísla
Prevod desatinného čísla na zlomok
Desatinné číslo roznásobíme pomocou mocniny desiatky tak, aby sme sa „zbavili“ desatinnej čiarky. Potom zlomok vykrátime (najväčším spoločným deliteľom), aby sme dostali zlomok v základnom tvare. Príklady:
1{,}5 = 1{,}5\cdot \frac{10}{10} = \frac{1{,}5\cdot 10}{10} = \frac{15}{10} = \frac{3}{2}
1{,}25 = 1{,}25 \cdot \frac{100}{100} = \frac{1{,}25\cdot 100}{100} = \frac{125}{100} = \frac{5}{4}
Počítanie nám môže uľahčiť, keď si zapamätáme niektoré užitočné prevody, s pomocou ktorých môžme vyriešiť aj ďalšie príklady:
0{,}01 = \frac{1}{100}
0{,}1 = \frac{1}{10}
0{,}2 = \frac{1}{5}
0{,}25 = \frac{1}{4}
0{,}333\ldots = \frac{1}{3}
0{,}5 = \frac{1}{2}
Prevod zlomku na desatinné číslo
Význam zlomku je jednoducho podiel čitateľa a menovateľa. Zlomok teda vyjadríme ako desatinné číslo jednoducho tak, že vydelíme čitateľ menovateľom (môže sa nám hodiť postup pre „delenie pod sebou“). Príklady:
\frac{3}{4} = 3:4 = 0{,}75
\frac{6}{5} = 6:5 = 1{,}2
\frac{3}{20} = 3:20 = 0{,}15

