Výpis prehľadov
Analytická geometria
Prechádzate súhrny informácií k určitým témam. Systémy Vieme sa zameriavajú hlavne na ich precvičovanie. K cvičeniam k jednotlivým podtémam sa dostanete pomocou odkazov nižšie.
Podkapitoly
- Analytická geometria
- Body
- Súradnice bodov v rovine
- Súradnice bodov v priestore
- Vzdialenosť bodov v rovine
- Vzdialenosť bodov v priestore
- Úsečky
- Dĺžka úsečky v rovine
- Stred úsečky v rovine
- Vzájomná poloha úsečiek v rovine
- Dĺžka úsečky v priestore
- Stred úsečky v priestore
- Vzájomná poloha úsečiek v priestore
- Vektory
- Vektory: pojmy
- Súradnice vektorov
- Veľkosť vektorov
- Vzájomná poloha vektorov
- Operácie s vektormi
- Vektory: násobenie konštantou, súčet, rozdiel
- Vektory: skalárny súčin
- Priamky
- Priamky: pojmy
- Určenie priamky
- Parametrické rovnice priamky v rovine
- Všeobecná rovnica priamky v rovine
- Smernicový tvar rovnice priamky
- Vzájomná poloha priamok v rovine
- Vzájomná poloha priamky a bodu v rovine
- Polohové úlohy
- Metrické úlohy
- Vzdialenosť bodu od priamky
- Odchýlka dvoch priamok
- Roviny
- Roviny: pojmy
- Parametrické rovnice roviny
- Všeobecná rovnica roviny
- Vzájomná poloha bodu a roviny
- Kužeľosečky
- Kružnica (kužeľosečka)
- Elipsa
- Parabola
- Hyperbola
Analytická geometria
Analytická geometria nám dovoľuje zapísať geometrické problémy algebraicky a vyriešiť ich pomocou rovníc.
Najjednoduchšie objekty popísateľné analyticky sú body, úsečky a vektory v rovine alebo v priestore. Keď už dokážeme manipulovať s vektormi, môžeme ich použiť napríklad k popisu priamky alebo roviny.
V prípade priamok a rovín stále ešte ide o objekty popísateľné lineárnymi rovnicami alebo sústavami lineárnych rovníc. Ak sa začneme zaoberať aj kvadratickými rovnicami, dokážeme popísať aj kužeľosečky v rovine, napríklad kružnicu, elipsu, parabolu a hyperbolu.
Dva významné typy problémov, ktoré riešime v rámci analytickej geometrie sú polohové úlohy, v ktorých vyšetrujeme vzájomnú polohu geometrických objektov, a metrické úlohy, v ktorých počítame konkrétnu číselnú hodnotu výsledku, ako je napr. vzdialenosť dvoch bodov alebo uhol zvieraný dvomi pretínajúcimi sa priamkami.
HoreAk sa zaoberáme bodmi v rovine alebo v priestore, kde máme zavedenú karteziánsku sústavu súradníc (v rovine s dvomi osami x,y alebo v priestore s tromi osami x,y,z), môžeme body popísať číselne súradnicami v rovine, prípadne súradnicami v priestore.
Pomocou súradníc potom dokážeme vypočítať vzdialenosť dvoch bodov „vzdušnou čiarou“ – dĺžku úsečky v rovine, prípadne v priestore.
HoreSúradnice bodov v rovine
Súradnice bodov väčšinou zapisujeme pomocou karteziánskej sústavy súradníc v rovine, ktorá má ako osi dve kolmé priamky. Vodorovná priamka sa tradične označuje x a súradnica pozdĺž tejto osi sa zapisuje prvá. Zvislá priamka sa tradične označuje y a súradnica pozdĺž tejto osi sa zapisuje druhá. Priamky x, y sa pretínajú v bode [0;0].
Priamky x a y sú súradnicové osi, bod [0;0] je počiatok sústavy súradníc.
Príklad: Súradnice bodu A
Bod A na obrázku je v danej sústave súradníc určený ako x=1, y=2, čo môžeme zapísať ako A[1;2].
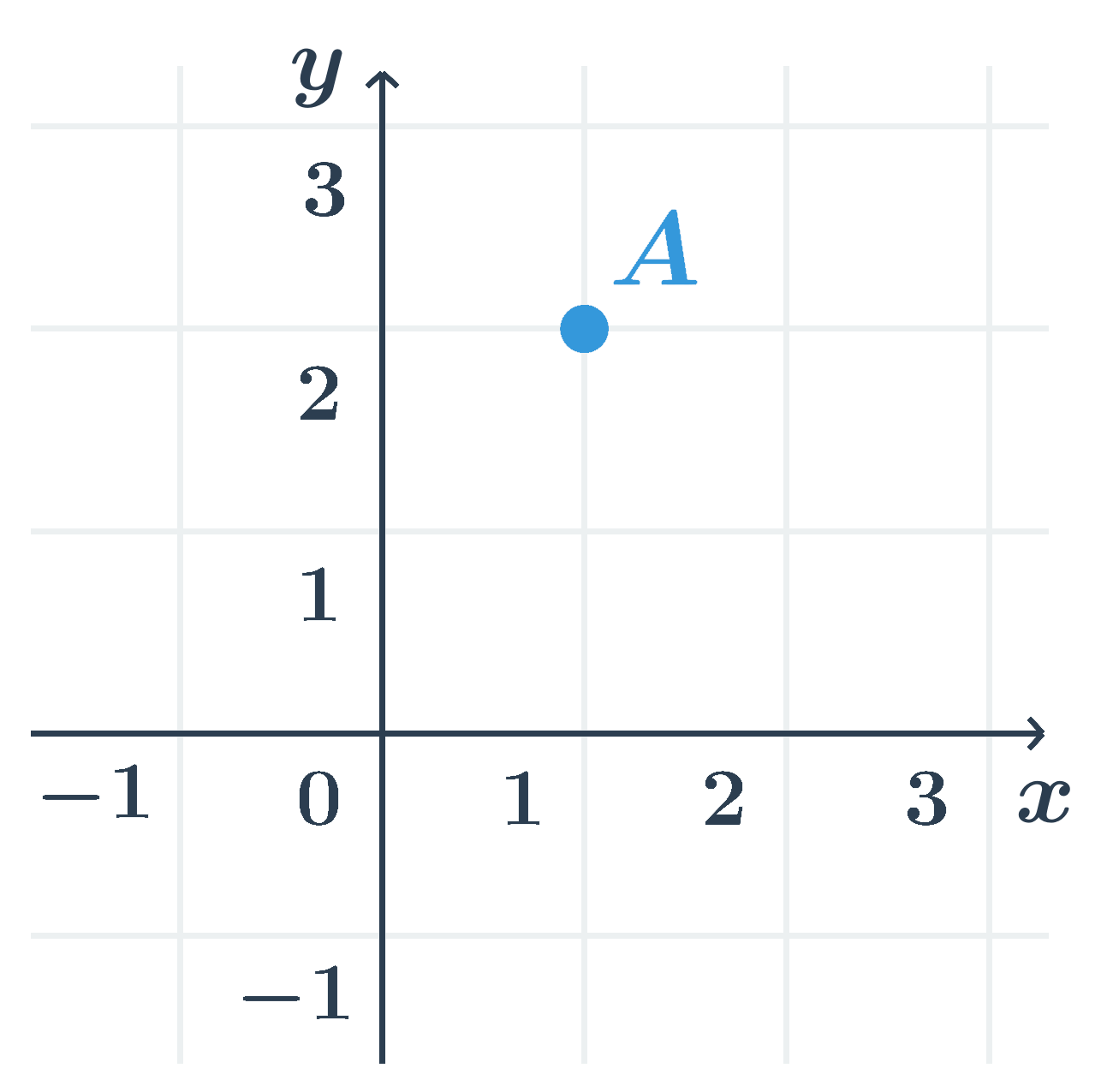
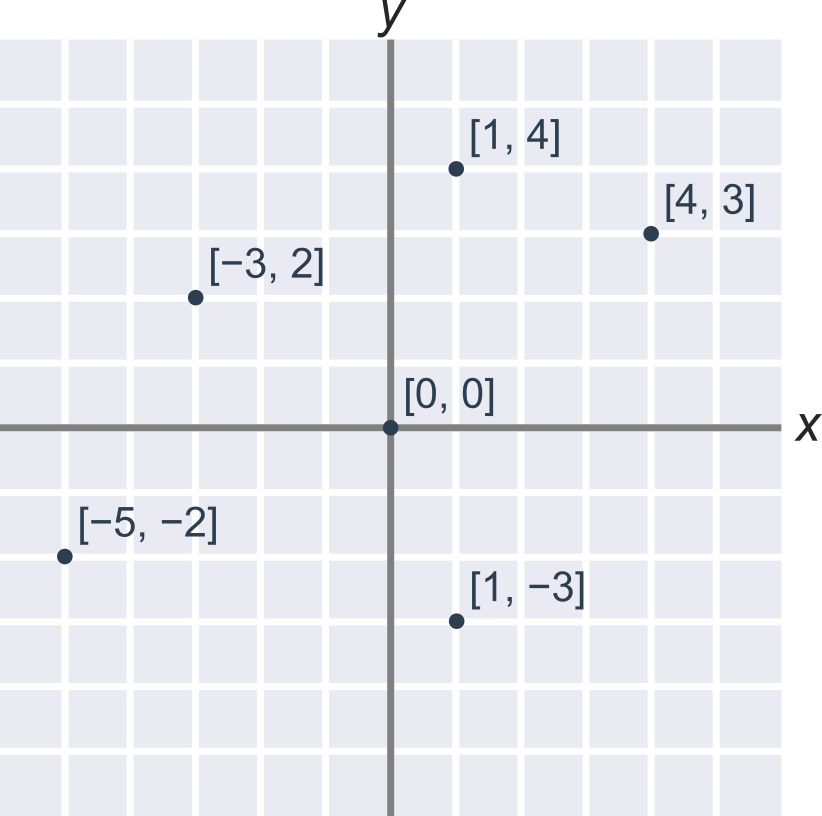
Ďalšie príklady súradníc bodov
Súradnice bodov v priestore
Kartézska sústava súradníc v rovine je daná trojicou navzájom kolmých číselných os x,y,z, ktoré sa pretínajú v bode [0;0;0].
Priamky x,y,z sú súradnicové osi v priestore, bod [0;0;0] je počiatok sústavy súradníc.
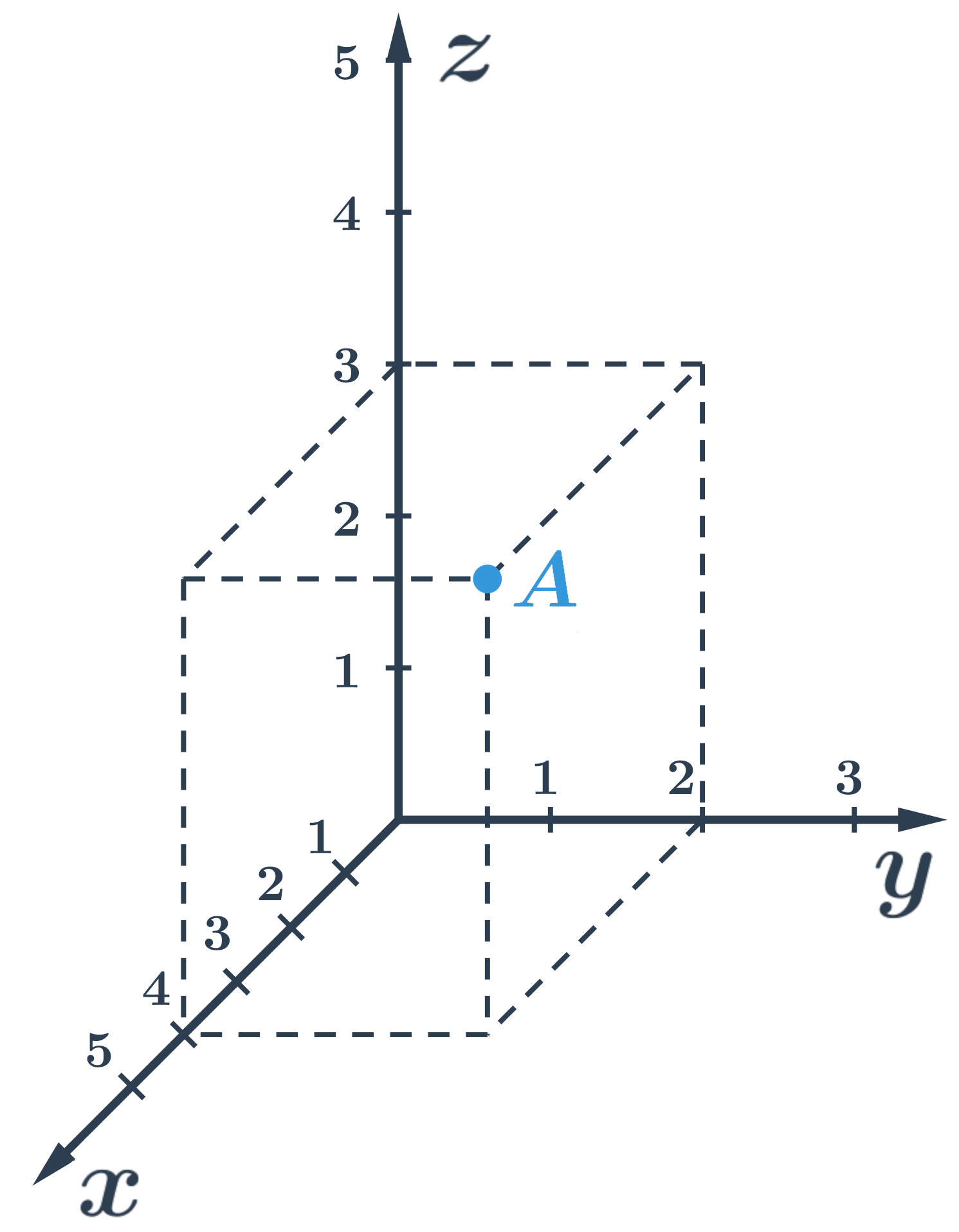
Príklad: Súradnice bodu A
Bod A na obrázku je v danej sústave súradníc určený ako x=4, y=2, z=3, čo môžeme zapísať ako A[4;2;3].
Vzdialenosť bodov v rovine
Vzdialenosť dvoch bodov v rovine môžeme vypočítať, keď poznáme ich súradnice.
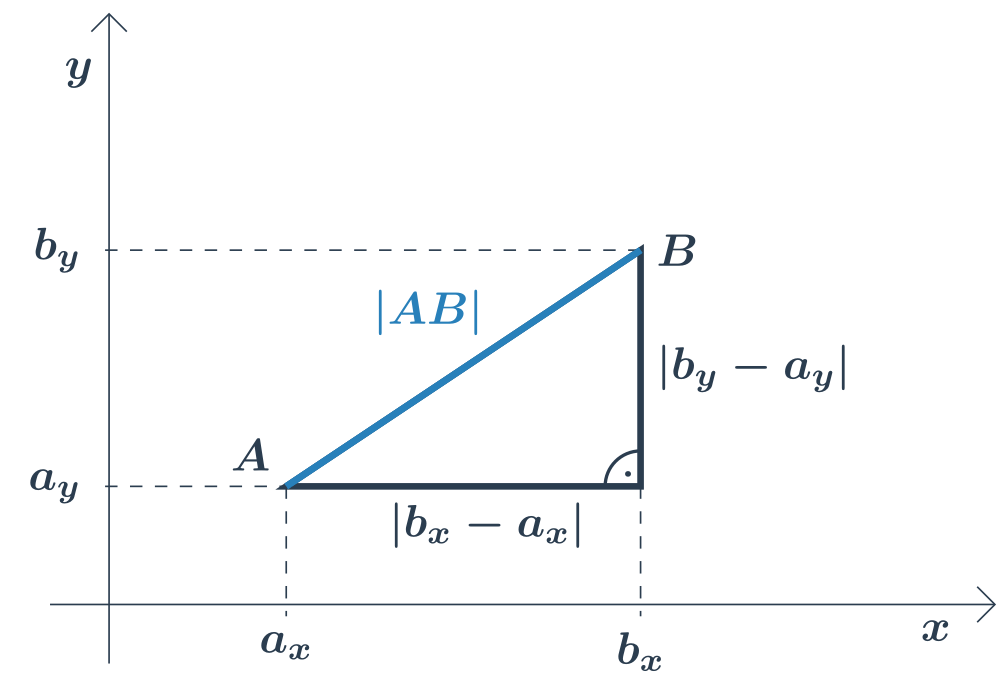
Ak sú dané súradnice A=[a_x,a_y], B=[b_x,b_y], je vzdialenosť bodu A od bodu B:
|AB| = \sqrt{(b_x-a_x)^2 + (b_y-a_y)^2}
Vzorec vychádza z Pytagorovej vety. Všimnime si pravouhlého trojuholníka s dĺžkami odvesien (b_x-a_x) a (b_y-a_y), ktorého prepona má dĺžku |AB|.
Príklad: vzdialenosť C[0;1],D[4;4]
- |CD| = \sqrt{(d_x-c_x)^2 + (d_y-c_y)^2}
- Dosadíme súradnice bodov C[0;1] a D[4;4]:
\sqrt{(4-0)^2 + (4-1)^2}=\sqrt{4^2 + 3^2}=\sqrt{25}=5 - Vzdialenosť je: |CD|=5
Príklad: vzdialenosť M[2;-1], N[-1;-2]
- |MN| = \sqrt{(n_x-m_x)^2 + (n_y-m_y)^2}
- Dosadíme súradnice bodov M[2;-1] a N[-1;-2]:
\sqrt{(-1-2)^2 + (-2-(-1))^2}=\sqrt{(-3)^2 + (-1)^2}=\sqrt{10} - Vzdialenosť je: |MN|=\sqrt{10}
Vzdialenosť bodov v priestore
Vzdialenosť dvoch bodov v priestore vypočítame podobne ako v rovine pomocou ich súradníc. Ak máme súradnice bodov A=[a_x,a_y,a_z], B=[b_x,b_y,b_z], môžeme ich vzdialenosť určiť takto:
|AB| = \sqrt{(b_x-a_x)^2 + (b_y-a_y)^2 + (b_z-a_z)^2}
Podobným spôsobom (dvakrát po sebe použijeme Pytagorovu vetu) počítame dĺžku telesovej uhlopriečky kvádra.
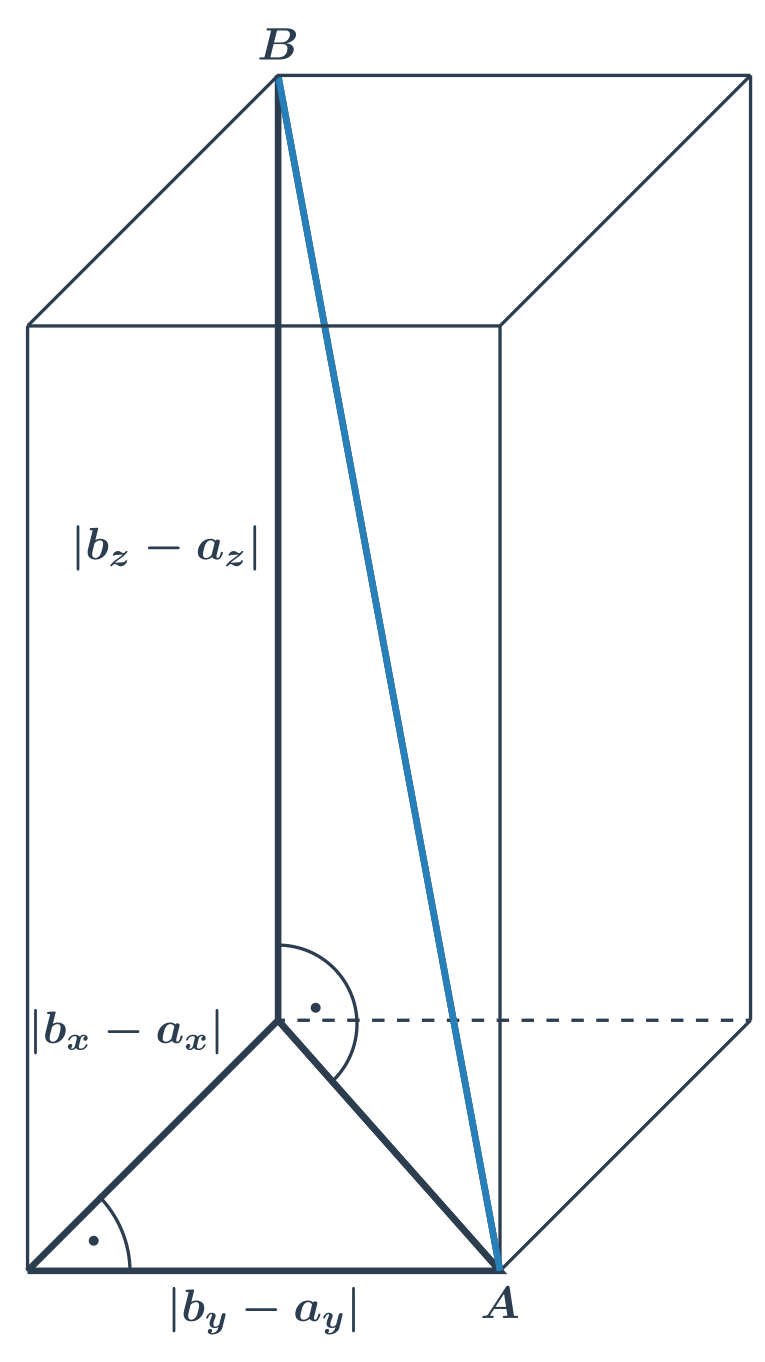
Príklad: vzdialenosť C[1;2;0],D[4;5;1]
- |CD| = \sqrt{(d_x-c_x)^2 + (d_y-c_y)^2 + (d_z-c_z)^2}
- Dosadíme súradnice bodov C[1;2;0] a D[4;5;1]: \sqrt{(4-1)^2 + (5-2)^2 + (1-0)^2}=\sqrt{3^2 + 3^2 + 1^2}=\sqrt{19}
- Vzdialenosť je: |CD|=\sqrt{19}
Príklad: vzdialenosť M[0;-1;3], N[-4;1;-1]
- |MN| = \sqrt{(n_x-m_x)^2 + (n_y-m_y)^2 + (n_y-m_y)^2}
- Dosadíme súradnice bodov M[0;-1;3] a N[-4;1;-1]: \sqrt{(-4-0)^2 + (1-(-1))^2 + (-1-3)^2}=\sqrt{(-4)^2 + 2^2+(-4)^2}=\sqrt{36}=6
- Vzdialenosť je: |MN|=6
Úsečka je časť priamky medzi dvomi krajnými bodmi (vrátane týchto bodov). Úsečka je v rovine aj v priestore jednoznačne zadaná svojimi krajnými bodmi.
HoreDĺžka úsečky v rovine
Dĺžku úsečky v rovine vypočítame rovnako ako vzdialenosť bodov v rovine.
Ak sú dané súradnice A[x_A; y_A], B[x_B; y_B], je dĺžka úsečky AB:
|AB| = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2}
Vzorec vychádza z Pytagorovej vety.
Je nutné počítať rozdiel súradníc v poradí „druhý bod mínus prvý“?
- Nie je. Výrazy x_B-x_A a x_A-x_B nie sú rovnaké. Ale sú opačné a vo vzorci počítame ich druhé mocniny, ktoré sa rovnajú.
- Naviac geometricky je dĺžka úsečky AB rovnaká ako dĺžka úsečky BA.
- Dôvodom zápisu práve v tomto tvare je fakt, že dĺžka úsečky je rovná veľkosti vektora \overrightarrow{AB} a pri vektore sa jeho veľkosť vždy počíta „koncový bod mínus počiatočný“.
Príklad: Dĺžka úsečky EF: E[0;-1], F[-4;2]
- |EF| = \sqrt{(x_F-x_E)^2 + (y_F-y_E)^2}
- Dosadíme súradnice bodov E[0;-1] a F[-4;2]: \sqrt{(-4-0)^2 + (2-(-1))^2}=\sqrt{4^2 + 3^2}=\sqrt{25}=5
- Dĺžka úsečky je: |EF|=5
Stred úsečky v rovine
Stred úsečky delí úsečku na dve rovnaké časti. Ak ležia krajné body úsečky AB na číselnej osi a ich polohám zodpovedajú hodnoty a a b, potom jej stredu S zodpovedá číslo s=\frac{a+b}{2}. Stred úsečky je „priemerom“ jej krajných bodov.
Pre úsečku v rovine bude situácia nasledujúca. 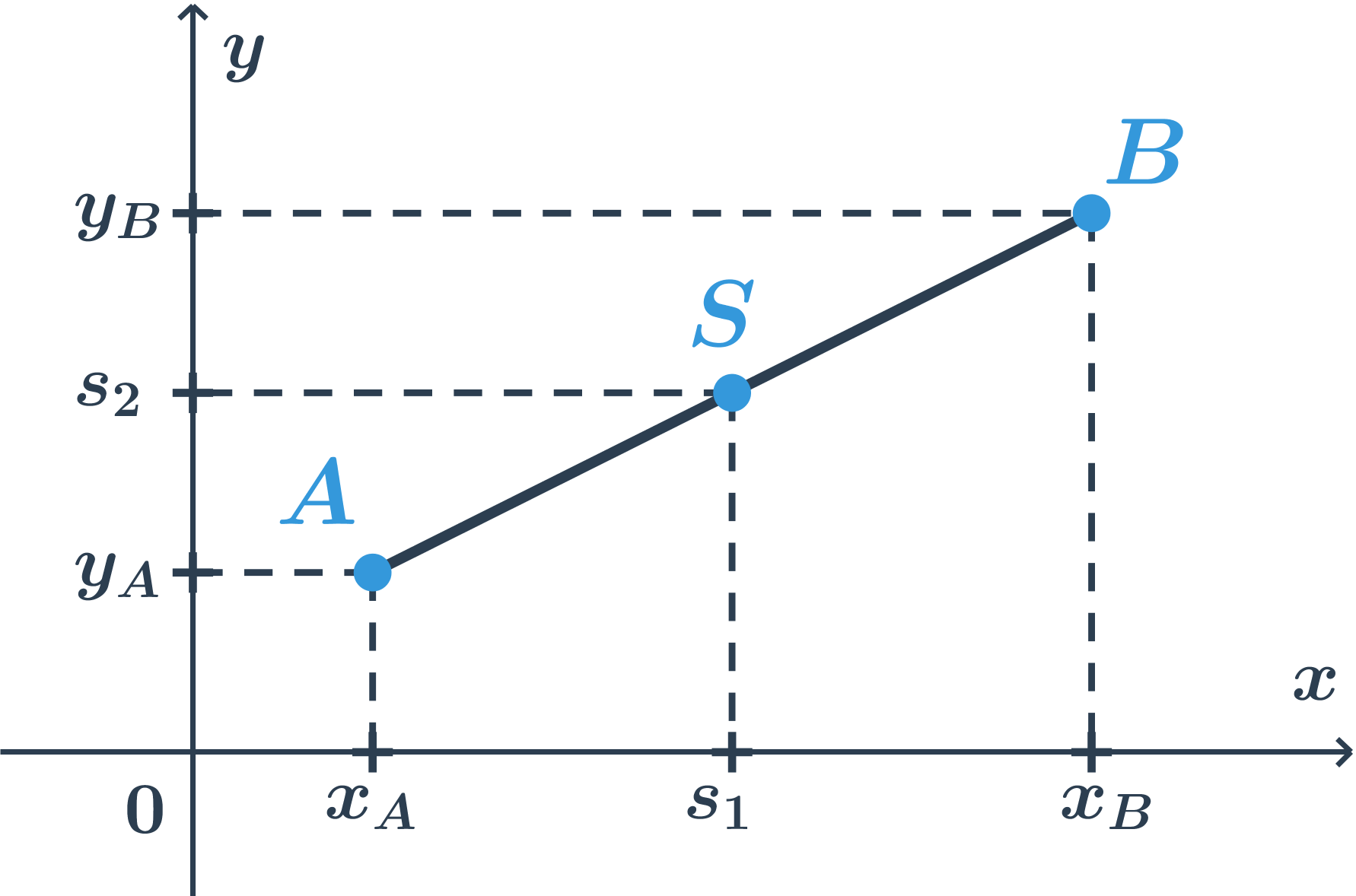 Situácia na oboch súradnicových osách je rovnaká ako predtým. Vypočítame obe súradnice stredu ako priemery zodpovedajúcich súradníc krajných bodov.
Situácia na oboch súradnicových osách je rovnaká ako predtým. Vypočítame obe súradnice stredu ako priemery zodpovedajúcich súradníc krajných bodov.
Pre stred S[s_1;s_2] úsečky AB, kde A[x_A; y_A], B[x_B; y_B] platí:
s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
Príklad: určenie stredu úsečky
Nájdite stred úsečky AB: A[6;-1], B[2;3]
- Pre súradnice stredu S[s_1;s_2] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
- Dosadíme súradnice bodov A[6;-1], B[2;3]: s_1 = \frac{6+2}{2}=4, s_2 = \frac{-1+3}{2}=1
- Stred úsečky AB je bod S[4;1]
Príklad: určenie druhého krajného bodu úsečky
Určite súradnice druhého krajného bodu úsečky AB, ak je daný bod A[-3;0] a jej stred S[1;3].
- Pre súradnice stredu S[s_1;s_2] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}
- Dosadíme súradnice bodov A[-3;0], S[1;3]: 1 = \frac{-3+x_B}{2}, 3 = \frac{0+y_B}{2}
- Dopočítame neznáme x_B, y_B: 2=-3+x_B\Rightarrow x_B=5\\ 6=0+y_B\Rightarrow y_B=6
- Bod B má súradnice [5;6].
Vzájomná poloha úsečiek v rovine
Dve úsečky v rovine môžu mať spoločné krajné body, potom hovoríme, že sú totožné. Ak sa úsečky pretínajú v jednom bode, hovoríme, že sú rôznobežné. Úsečky sa tiež nemusia pretínať, nemajú teda žiadny spoločný bod. Špeciálne môžu v tomto prípade byť rovnobežné.
HoreDĺžka úsečky v priestore
Dĺžku úsečky v priestore vypočítame rovnako ako vzdialenosť bodov v priestore.
Ak sú dané súradnice A[x_A; y_A;z_A], B[x_B; y_B;z_B], je dĺžka úsečky AB:
|AB| = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2+(z_B-z_A)^2}
Príklad: Dĺžka úsečky EF: E[-2;0;1], F[-4;2;0]
- |EF| = \sqrt{(x_F-x_E)^2 + (y_F-y_E)^2+ (z_F-z_E)^2}
- Dosadíme súradnice bodov EF; E[-2;0;1], F[-4;2;0]:
\sqrt{(-4-(-2))^2 + (2-0)^2+(0-1)^2}=\sqrt{(-2)^2 + 2^2+(-1)^2}=\sqrt{4+4+1}=\sqrt{9}=3 - Dĺžka úsečky je: |EF|=3
Stred úsečky v priestore
Stred úsečky v priestore vypočítame podobne ako stred úsečky v rovine. Vypočítame všetky súradnice stredu ako priemery zodpovedajúcich súradníc krajných bodov.
Pre stred S[s_1;s_2;s_3] úsečky AB, kde A[x_A; y_A;z_A], B[x_B; y_B;z_B] platí:
s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2} , s_3 = \frac{z_A+z_B}{2}
Príklad: určenie stredu úsečky
Nájdite stred úsečky AB: A[2;1;-3], B[2;-3;3]
Pre súradnice stredu S[s_1;s_2;s_3] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}, s_3 = \frac{z_A+z_B}{2}
Dosadíme súradnice bodov A[2;1;-3], B[2;-3;3].
s_1 = \frac{2+2}{2}=2, s_2 = \frac{1-3}{2}=-1, s_3 = \frac{-3+3}{2}=0
Stred úsečky AB je bod S[2;-1;0]
Príklad: určenie druhého krajného bodu úsečky
Určite súradnice druhého krajného bodu úsečky AB, ak je daný bod A[1;2;4] a jej stred S[1;-3;0].
- Pre súradnice stredu S[s_1;s_2;s_3] platí: s_1 = \frac{x_A+x_B}{2}, s_2 = \frac{y_A+y_B}{2}, s_3 = \frac{z_A+z_B}{2}
- Dosadíme súradnice bodov A[1;2;4], S[1;-3;0].
- 1 = \frac{1+x_B}{2}, -3 = \frac{2+y_B}{2}, 0 = \frac{4+z_B}{2}
- Dopočítame neznáme x_B, y_B, z_B:
\begin{array}{rclcrcr} 2&=&1+x_B &\Rightarrow& x_B&=&1\\ -6&=&2+y_B &\Rightarrow& y_B&=&-8\\ 0&=&4+z_B&\Rightarrow& z_B&=&-4 \end{array}
- Bod B má súradnice [2;-8;-4].
Vzájomná poloha úsečiek v priestore
Podobne ako v rovine môžu mať dve úsečky spoločné krajné body, potom hovoríme, že sú totožné. Ak sa úsečky pretínajú v jednom bode, hovoríme, že sú rôznobežné. Úsečky sa tiež nemusia pretínať, nemajú teda žiadny spoločný bod. Špeciálne môžu v tomto prípade byť rovnobežné.
HoreVektor je množina všetkých zhodne orientovaných úsečiek, ktoré majú rovnakú dĺžku. Každú z týchto úsečiek nazývame umiestnením vektora.
Vektor je určený počiatočným a koncovým bodom, graficky znázorňujeme so šípkou pri koncovom bode, zapisujeme: \vec{u}=\overrightarrow{AB}
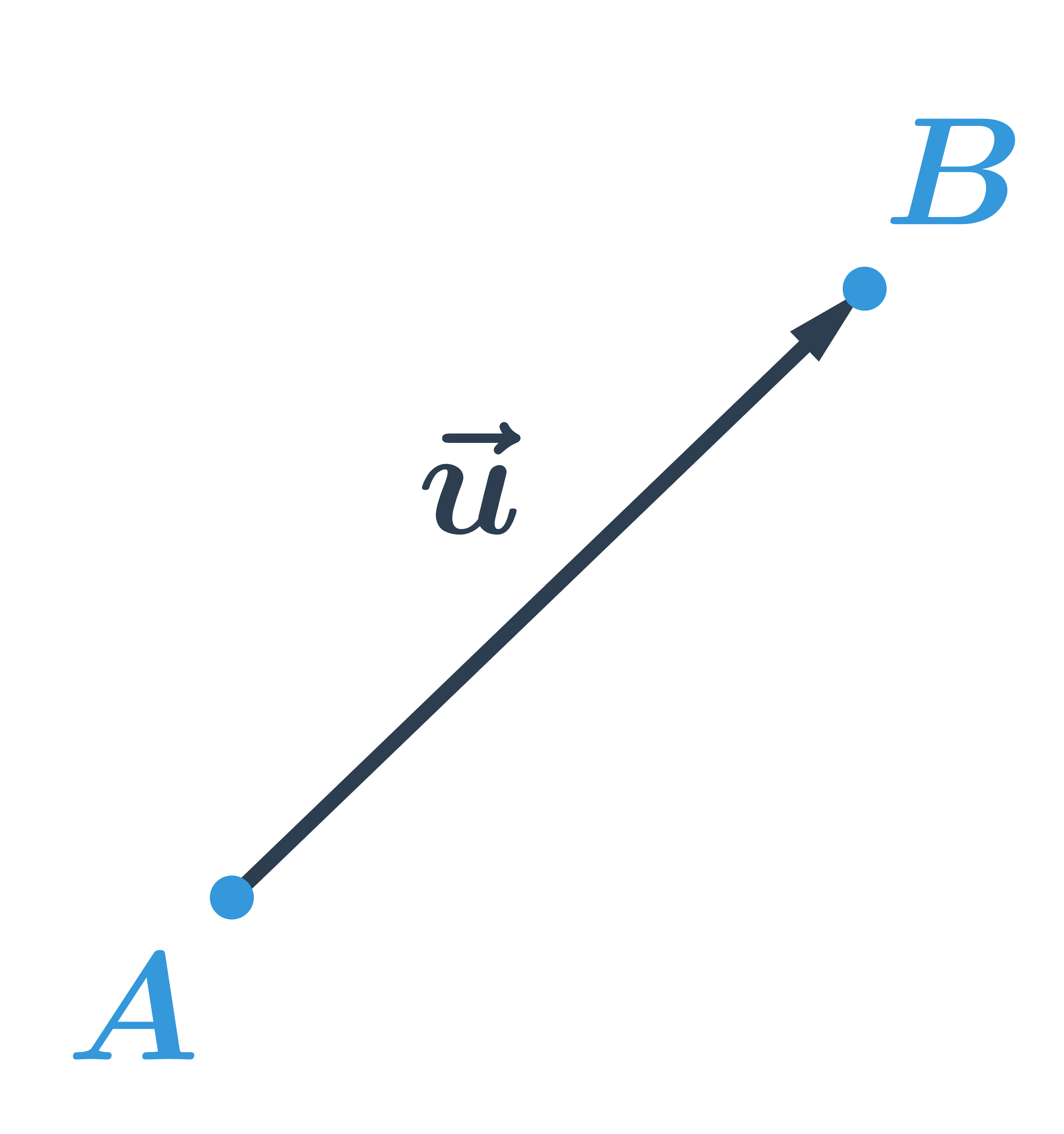
Na obrázku je A počiatočný bod vektora \vec{u}, B je koncový bod vektora \vec{u}.
HoreVektory: pojmy
Opačné vektory sú vektory, ktoré majú rovnakú dĺžku a opačnú orientáciu:
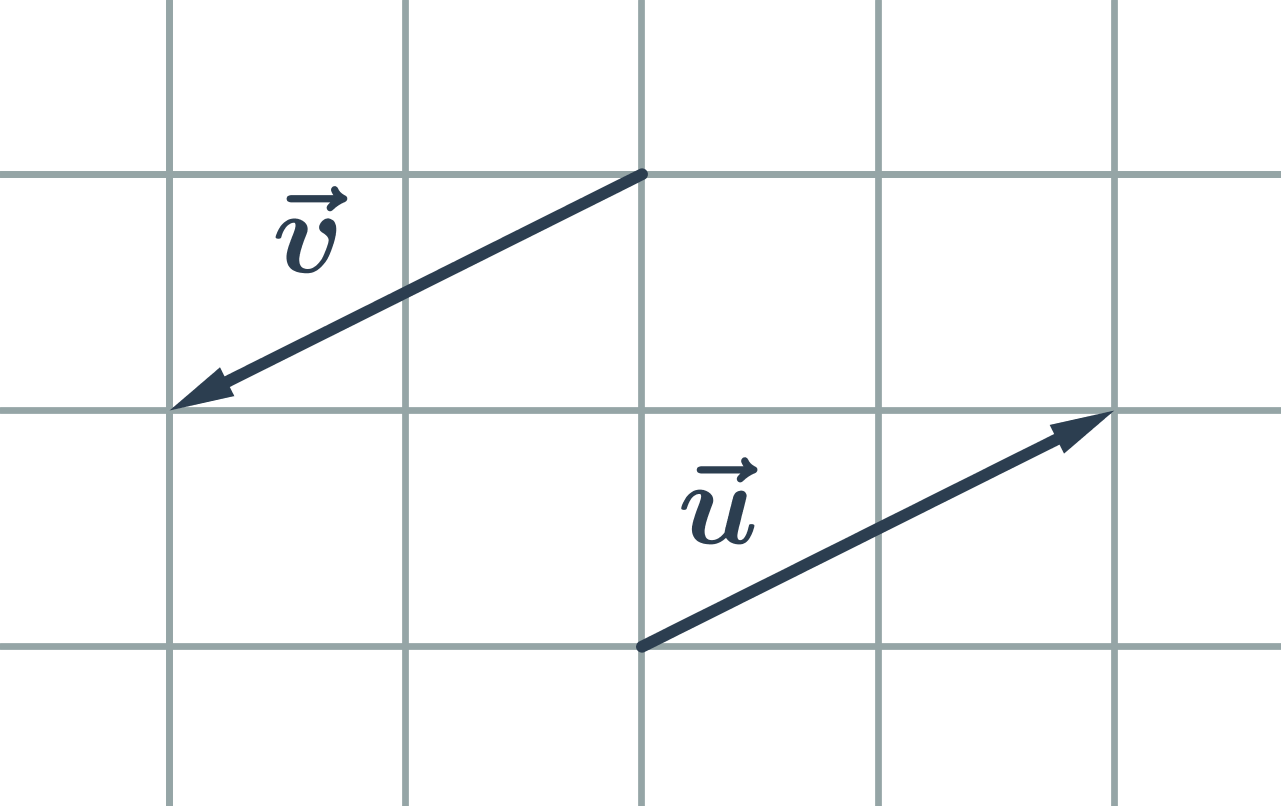
Kolineárne vektory sú vektory, ktoré môžeme umiestniť na jednu priamku. Teda nemusia mať rovnakú dĺžku, môžu mať rovnakú alebo opačnú orientáciu:
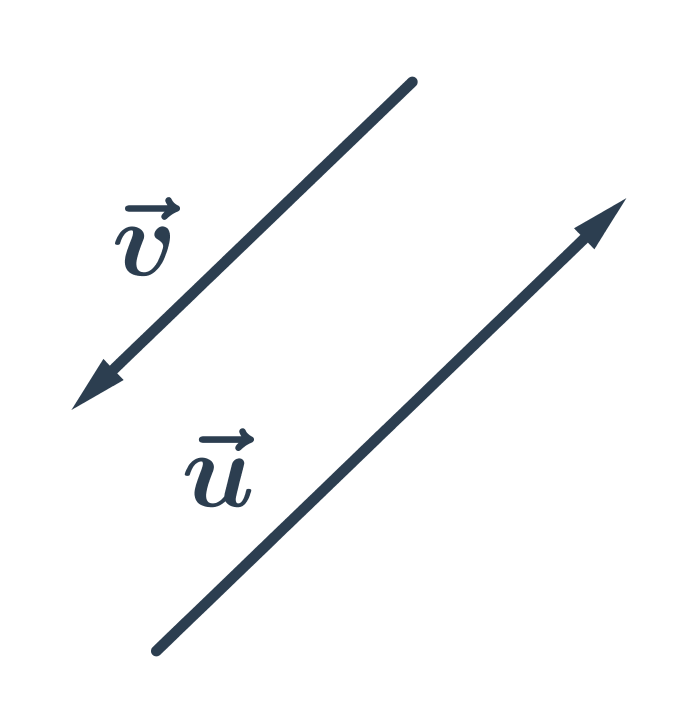
Kolmé vektory sú vektory, ktoré zvierajú pravý uhol:
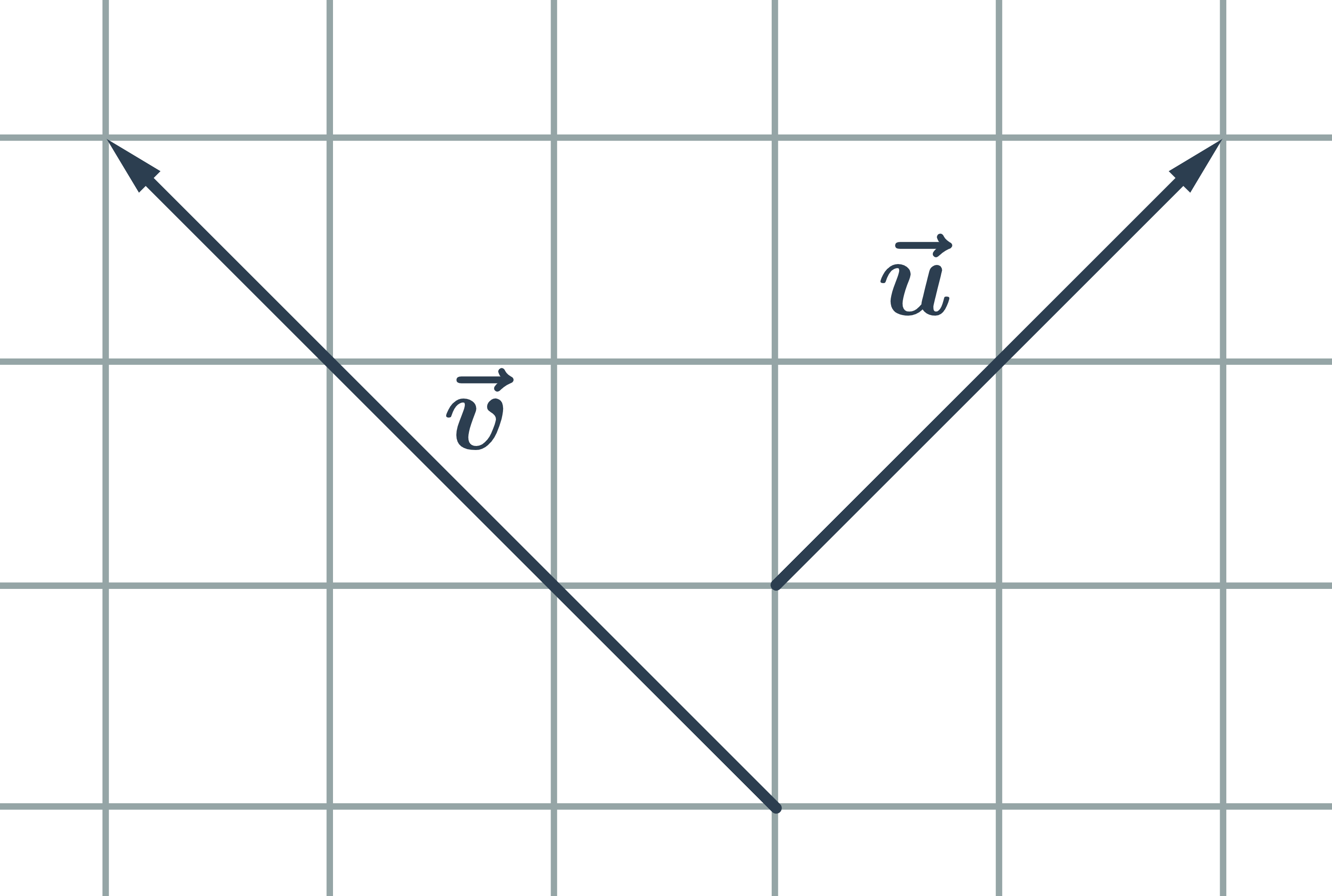
Súradnice vektora sú pravouhlé priemety vektora do súradnicových osí, teda vektor \vec{u}=\overrightarrow{AB} má súradnice: \vec{u}=(u_1;u_2)=(b_1-a_1;b_2-a_2)
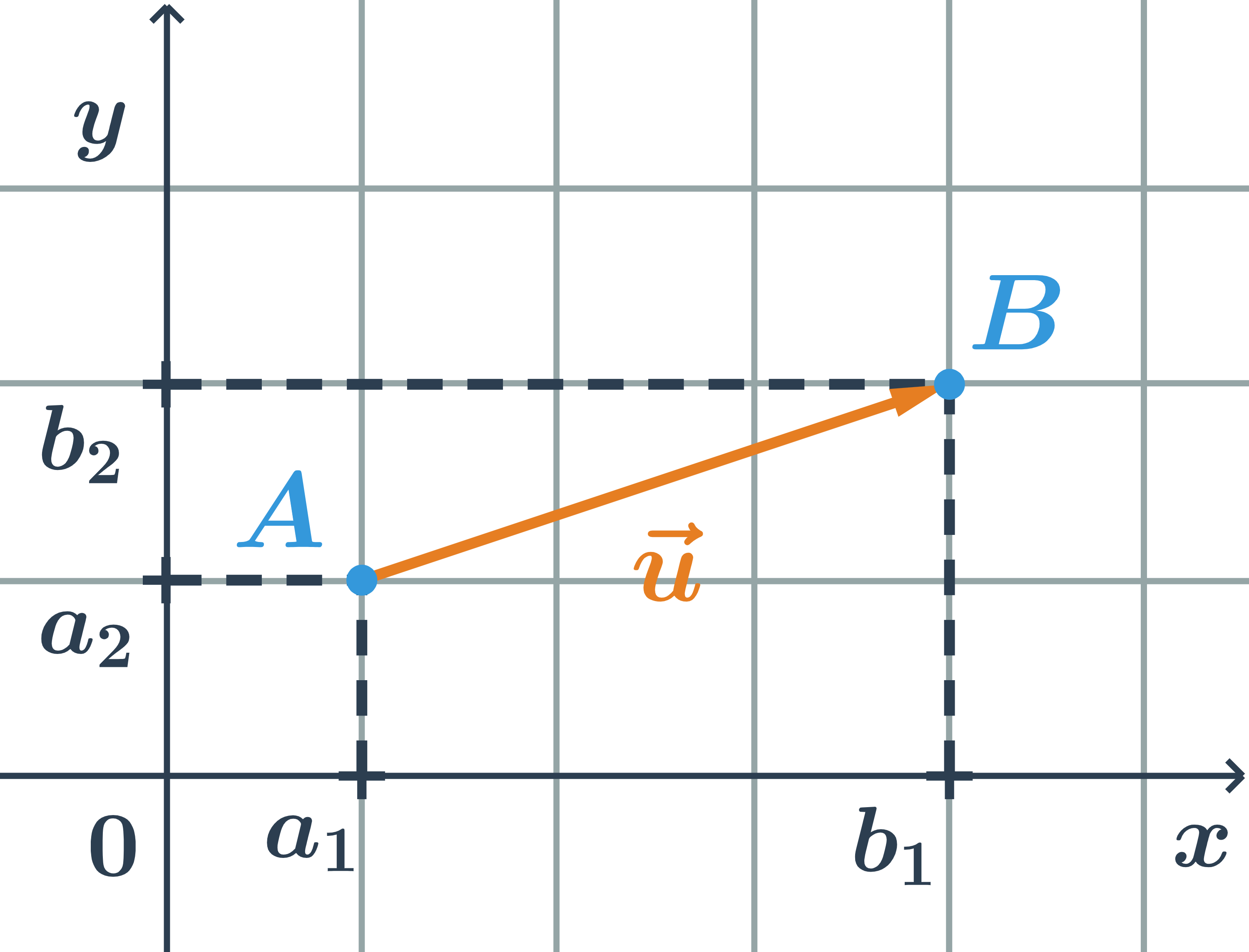
Veľkosť vektora \vec {u}=\overrightarrow{AB} je dĺžka úsečky AB, značíme \left| \vec{u} \right| a platí: \left| \vec{u} \right|=\sqrt{u_1^2+u_2^2}
Jednotkový vektor má dĺžku 1.
Nulový vektor má nulovú dĺžku, teda splýva jeho počiatočný a koncový bod.
HoreSúradnice vektorov
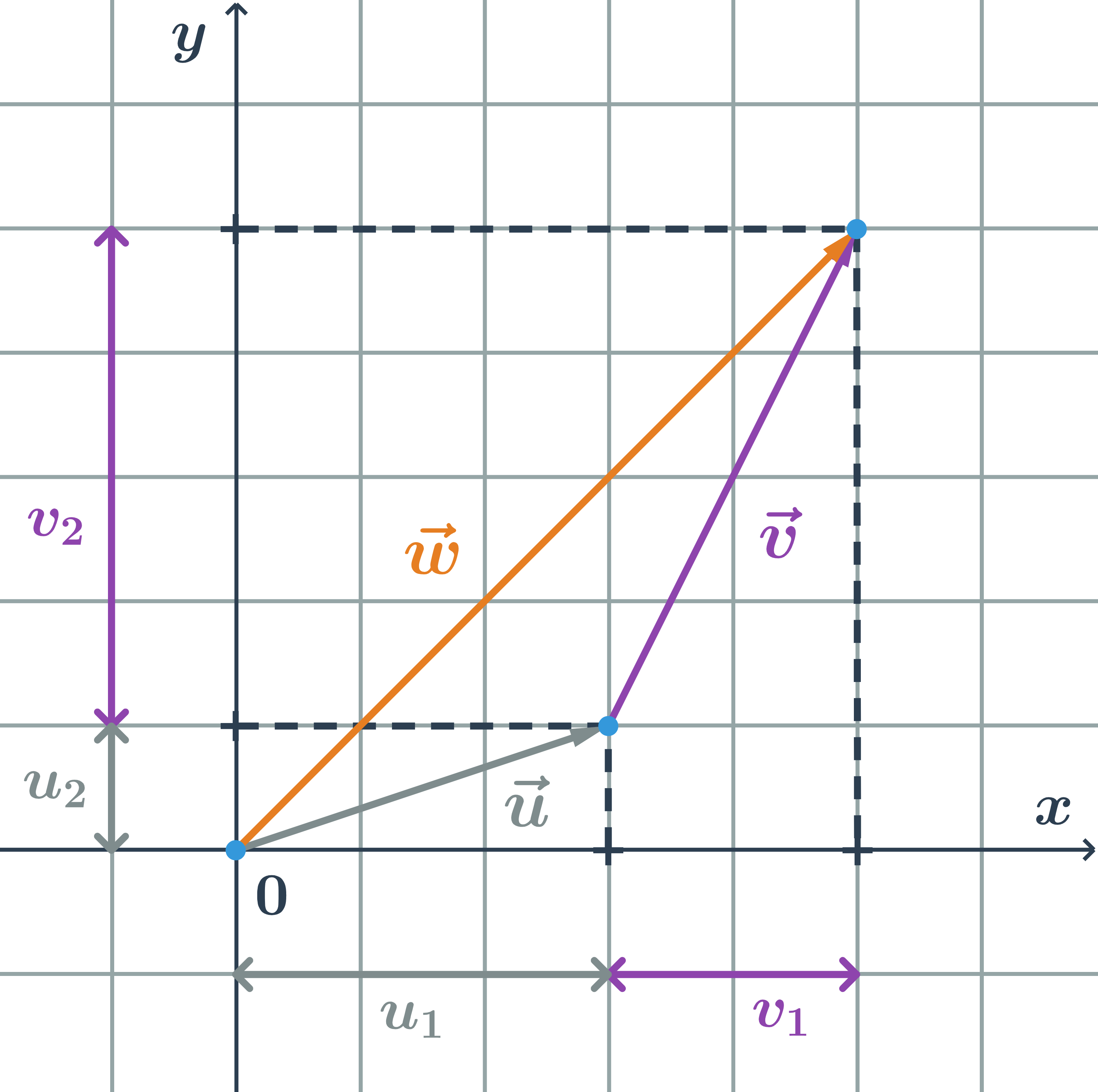
Už vieme, že vektor je množina nekonečne veľa orientovaných úsečiek, jedna z nich má počiatok v počiatku súradnicového systému, v bode O=[0;0]. Súradnice koncového bodu sú súradnice daného vektora.
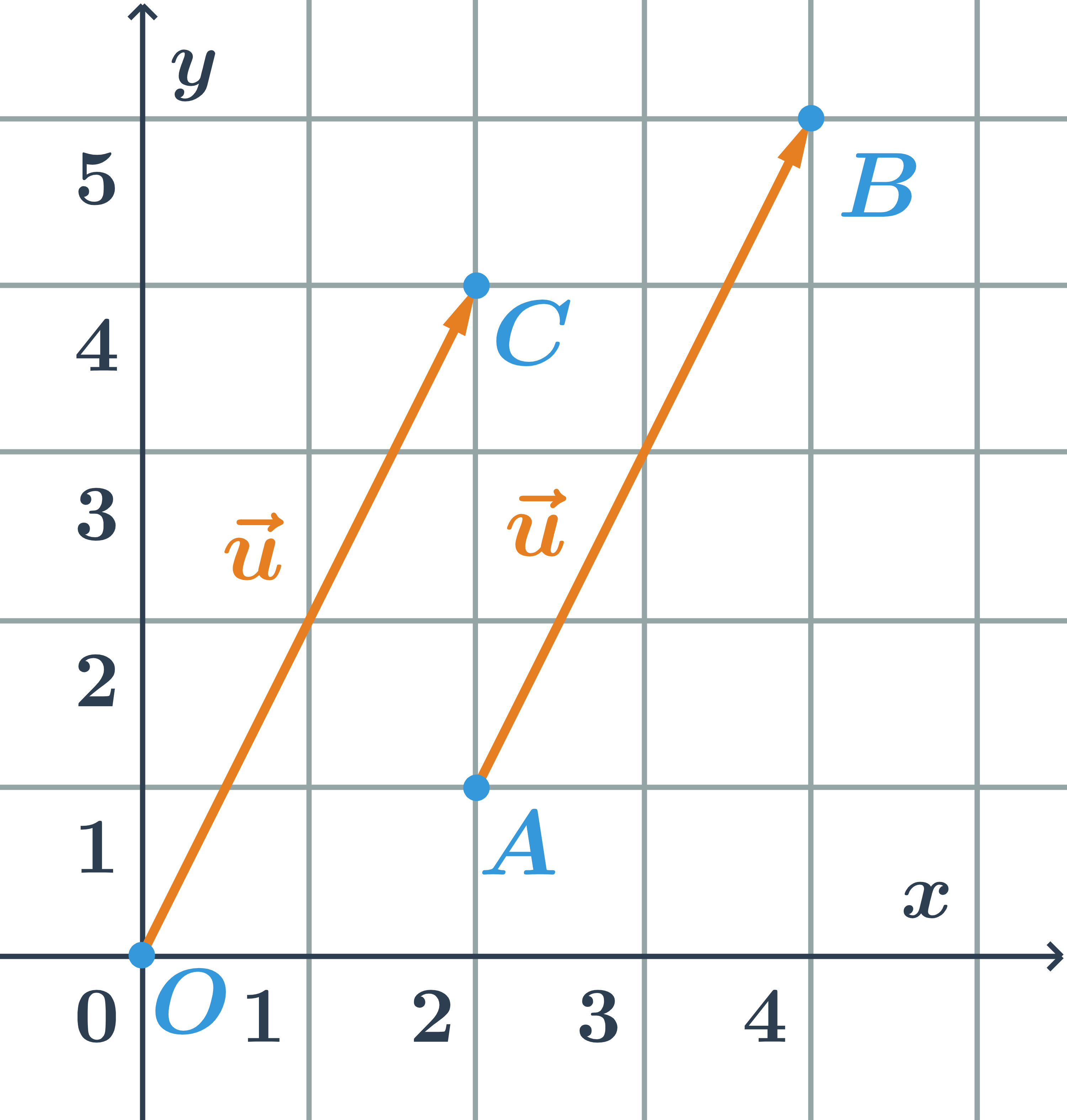
Súradnice vektora \overrightarrow{AB}
- Ak chceme vektor \overrightarrow{AB} posunúť do počiatku súradnicového systému, posunieme ho o dva štvorčeky vľavo a o jeden štvorček dole.
- Bod A sa posunie do bodu O, bod B sa posunie do bodu C. Tento posun môžeme vyjadriť takto:
- A sa posunie na [2-2;1-1]=[0;0]
- B sa posunie na [4-2;5-1]=[2;4]
- Súradnice vektora na obrázku sú: \vec{u}=\overrightarrow{AB}=\overrightarrow{OC}=(2;4)
Všimnite si, že súradnice vektora \overrightarrow{AB} sme získali odčítaním súradníc bodu A od súradníc bodu B
Pre súradnice vektora \overrightarrow{AB} určeného bodmi A=[a_1;a_2], B=[b_1;b_2] platí: \overrightarrow{AB}=B-A=(b_1-a_1;b_2-a_2)
HoreVeľkosť vektorov
Veľkosť vektora \overrightarrow{AB} je dĺžka úsečky AB. Vektor, ktorý má dĺžku 1, sa nazýva jednotkový vektor:
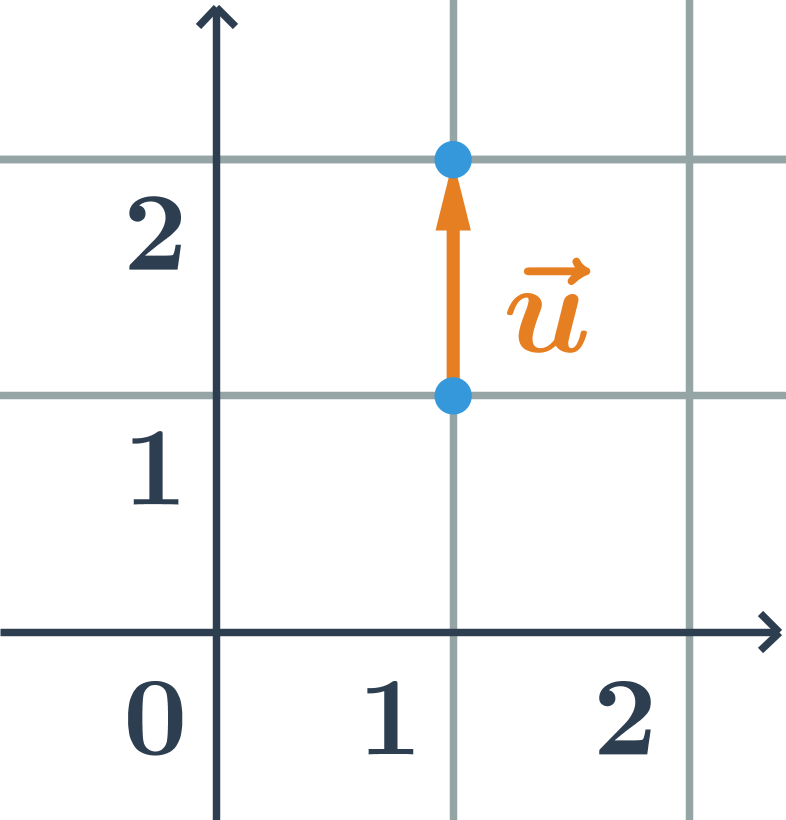
Vektor, ktorý má nulovú dĺžku (počiatočný a koncový bod vektora splýva) sa nazýva nulový vektor:
Veľkosť vektora \vec{u}=(u_1;u_2) určíme s využitím Pytagorovej vety: \left| \vec{u} \right|=\sqrt{u_1^2+u_2^2}
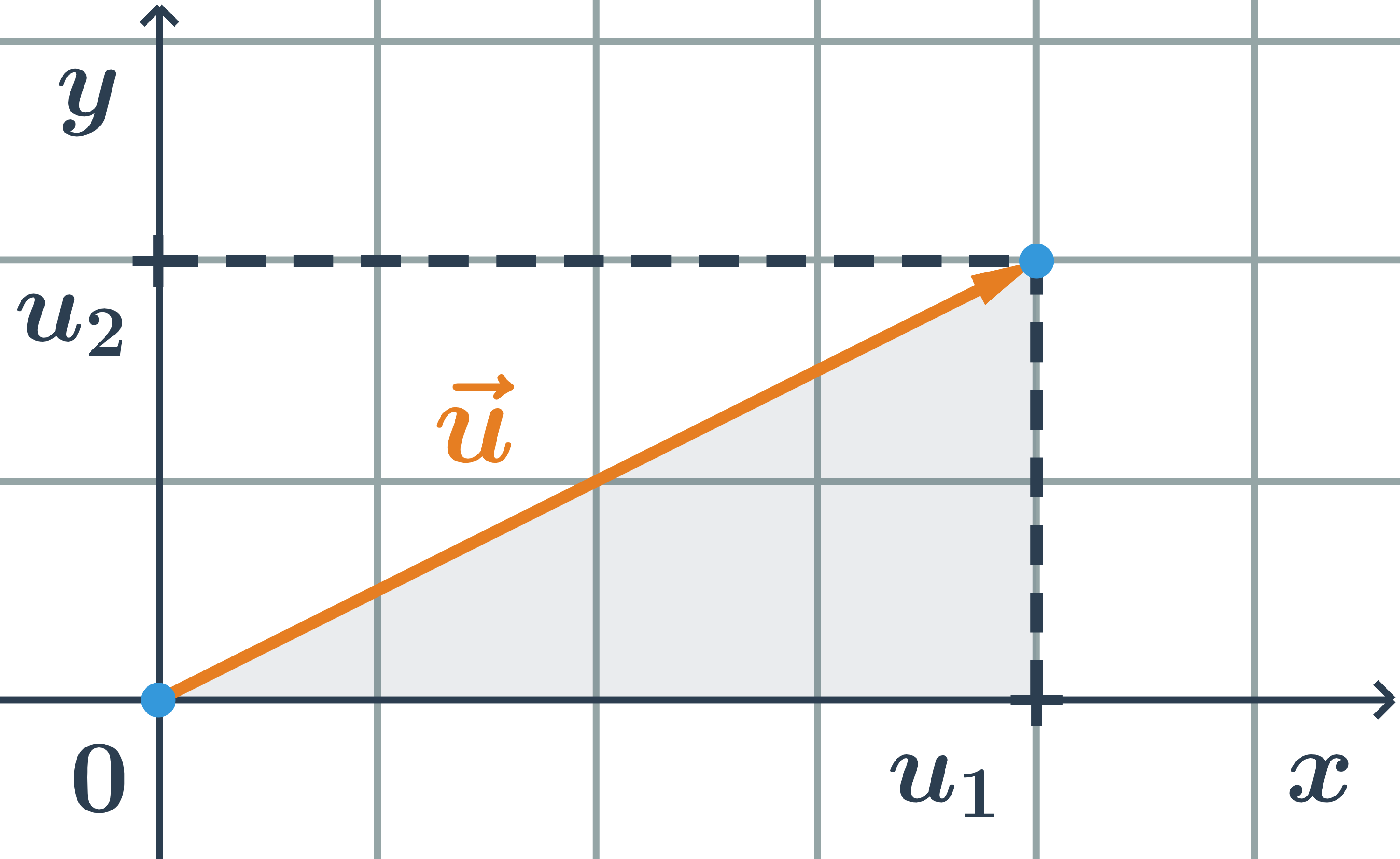
Vo vyfarbenom trojuholníku je dĺžka vektora prepona, odvesny majú dĺžky u_1 a u_2.
Príklad: veľkosť vektora
Určite veľkosť vektora na obrázku:
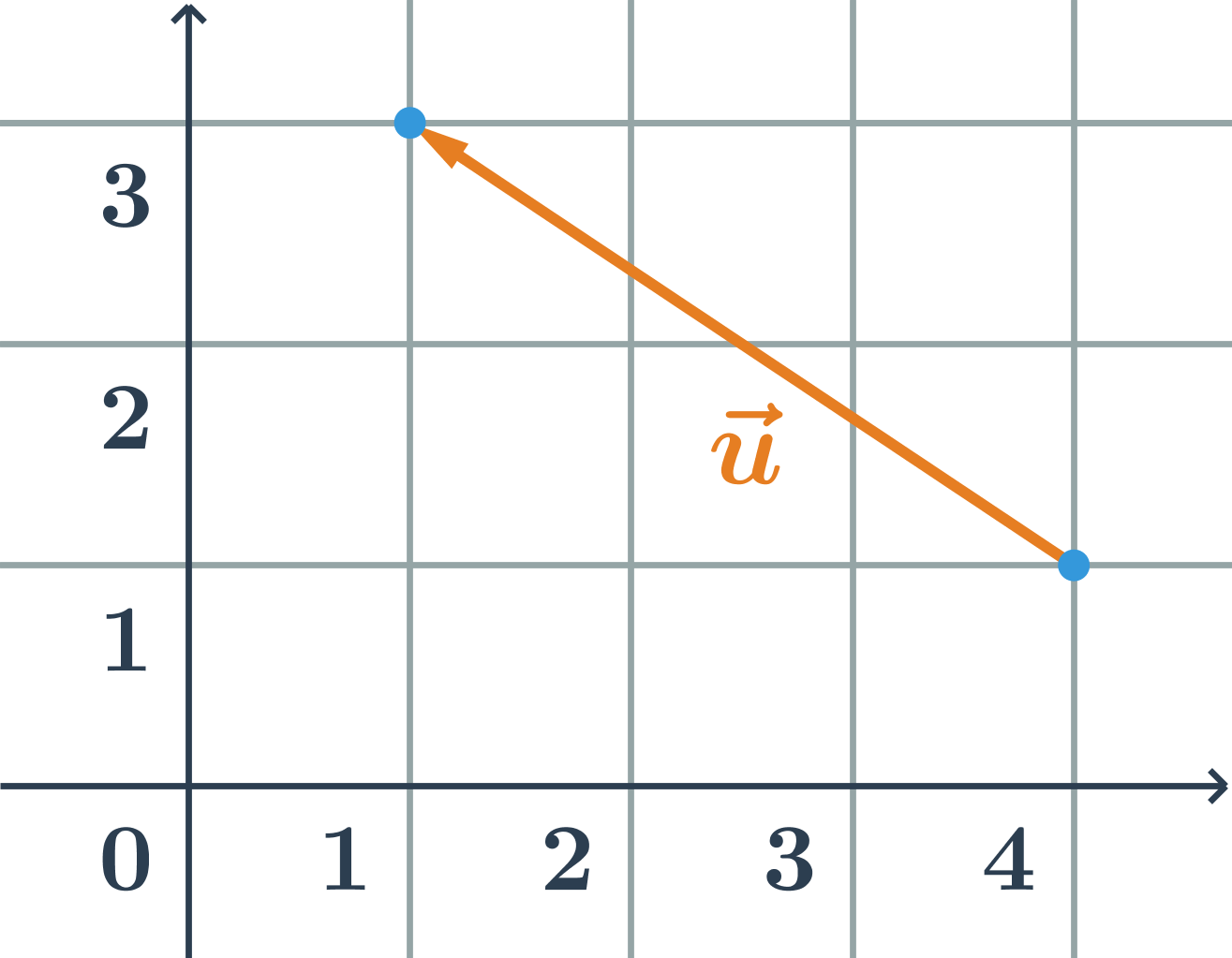
Vektor na obrázku má súradnice \vec{u}=(-3;2), jeho veľkosť je \left| \vec{u} \right|=\sqrt{(-3)^2+2^2}=\sqrt{(-3)^2+2^2}=\sqrt{13}
Vzájomná poloha vektorov
Opačné vektory sú vektory, ktoré majú rovnakú dĺžku a opačnú orientáciu. K vektoru \vec{u}=(u_1;u_2) je opačný vektor \vec{v}=(-u_1;-u_2)
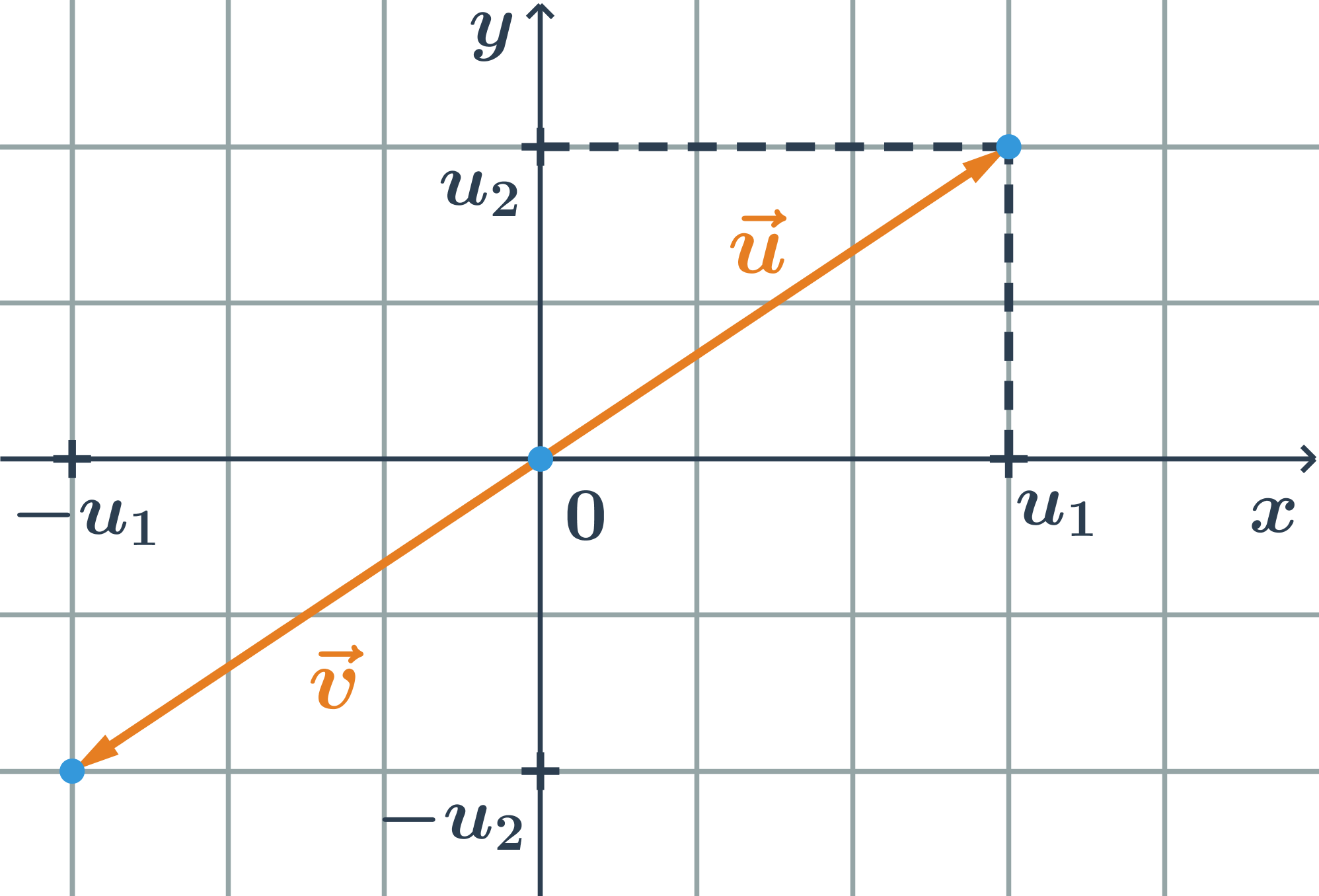
Príklad opačný vektor
- Určite opačný vektor k vektoru \vec{u}=(3;-1).
- Opačný vektor \vec{v} k vektoru \vec{u} má súradnice: (-u_1;-u_2)=(-3;1)
Kolineárne vektory sú vektory, ktoré môžeme umiestniť na jednu priamku. S vektorom \vec{u}=(u_1;u_2) je kolineárny každý vektor \vec{v}=(k\cdot u_1;k \cdot u_2), kde k je reálne nenulové číslo. Pre k > 0 majú vektory rovnaký smer, pre k < 0 majú vektory opačný smer.
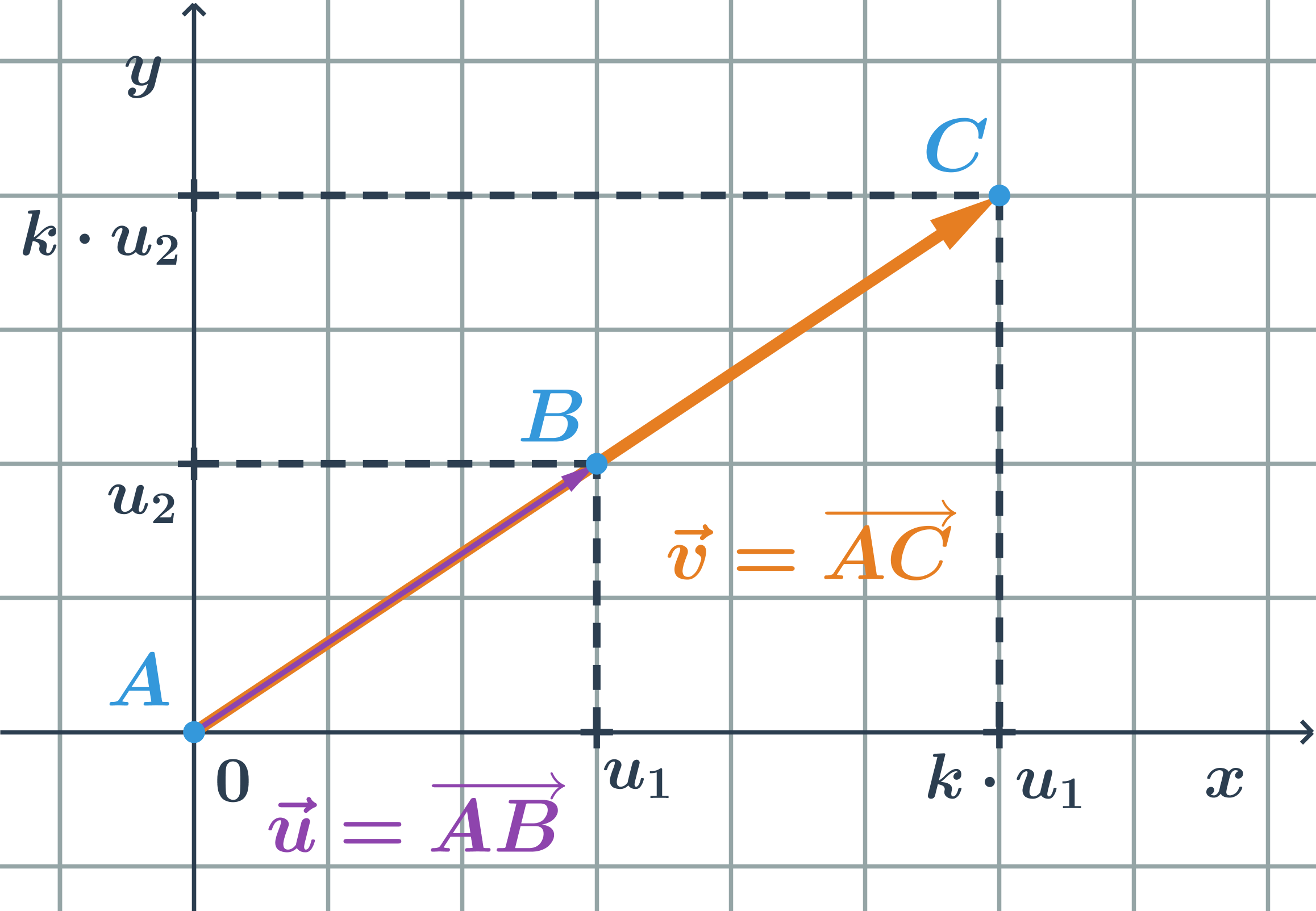
Príklad kolineárny vektor
- Doplňte súradnicu vektora \vec{v}=(v_1;3) tak, aby bol kolineárny s vektorom \vec{u}=(2;-1).
- Pre druhú súradnicu platí: v_2=3, u_2=-1, teda v_2= (-3) \cdot u_2
- Vidíme, že k=-3 je záporné, teda \vec{u} a \vec{v} majú opačnú orientáciu
- Pre prvú súradnicu musí platiť: v_1= (-3) \cdot u_1= (-3)\cdot2=-6.
Kolmé vektory sú vektory, ktoré zvierajú pravý uhol Na vektor \vec{u}=(u_1;u_2) je kolmý každý vektor \vec{v}=(-k\cdot u_2;k \cdot u_1), kde k je reálne nenulové číslo.
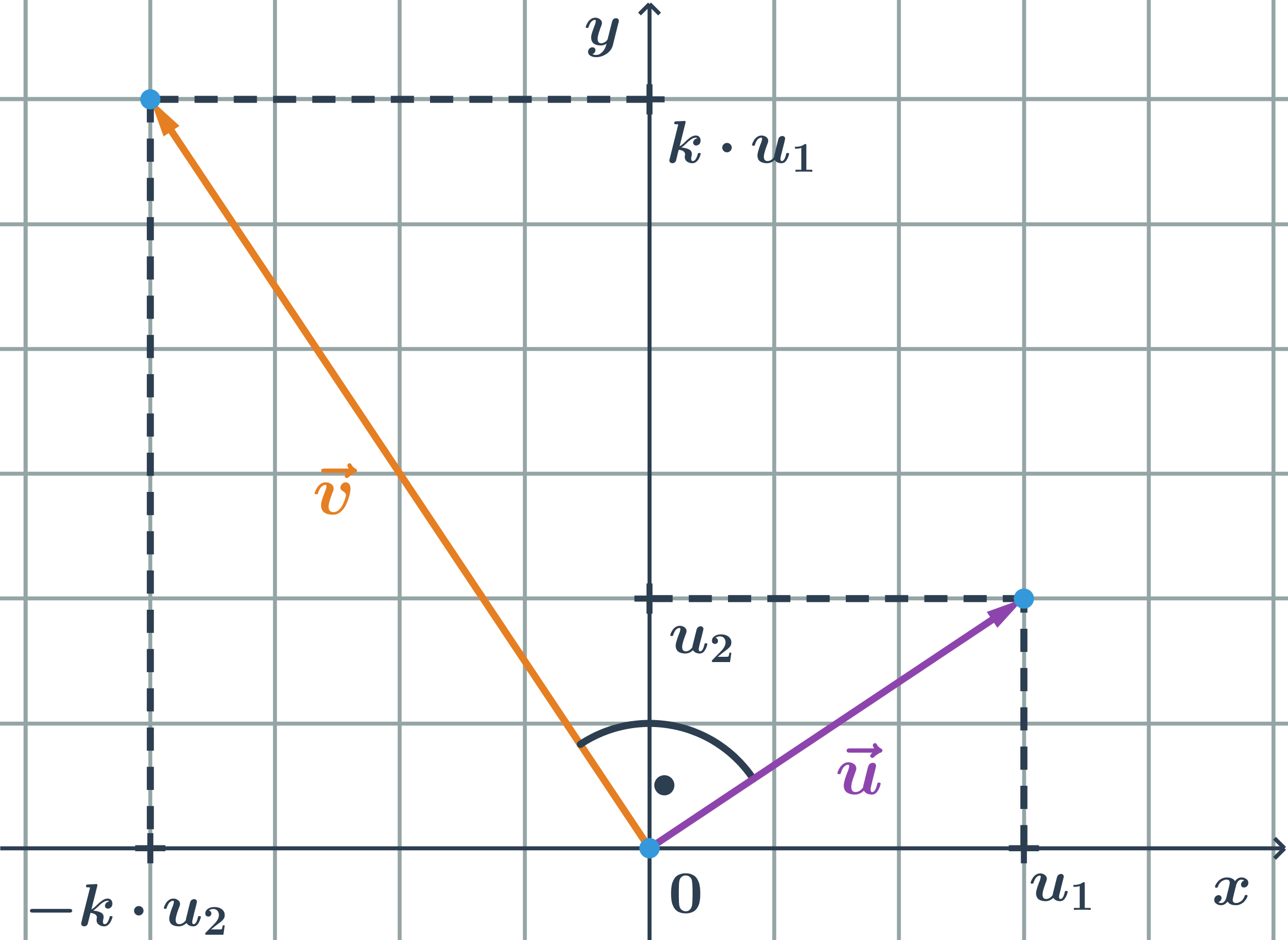
Príklad kolmý vektor
- Doplňte súradnicu vektora \vec{v}=(v_1;4) tak, aby bol kolmý k vektoru \vec{u}=(2;-1).
- Platí: v_2=2 \cdot u_1, teda musí platiť: v_1 = - 2 \cdot u_2.
- Máme teda v_1 = - 2 \cdot u_2 = -2 \cdot (-1) = 2.
Operácie s vektormi
Vektory v rovine môžu byť zapísané ako dvojice čísel – súradníc v rovine, podobne trojrozmerné vektory je možné zapísať ako trojice čísel – súradníc v priestore.
Operácie ako súčet, rozdiel a vynásobenie reálnym číslom, ktoré vieme jednoducho vykonávať s číslami, je možné s vektormi vykonávať po jednotlivých súradniciach. Tým sa zaoberá kapitolka Vektory: násobenie konštantou, súčet, rozdiel. Príklady praktického použitia týchto operácií s vektormi:
- vrabec letí rovnakým smerom ako mucha a dvakrát rýchlejšie než mucha – vektor rýchlosti vrabca získame, keď vektor rýchlosti muchy vynásobíme konštantou 2,
- satelitné snímky ukazujú, že ráno ešte vozidlo Marka Watneyho stálo na marsovskej základni, za dnes prekonal 50 km na východ – jeho novú polohu získame, keď k súradniciam základne pripočítame vektor (50;0),
- slimák preliezol rovno po monitore z ľavého horného rohu (súradnice v pixeloch [0;0]) do bodu [1007;555] – vektor, ktorého súradnice sú počty pixelov, ktoré slimák prekonal v horizontálnom a vertikálnom smere, získame ako rozdiel jeho umiestnenia na konci pohybu a jeho umiestnenia na začiatku pohybu.
Špeciálna operácia, ktorú je možné vykonať s dvomi vektormi rovnakej dimenzie (majú rovnaký počet súradníc), je skalárny súčin. Vstup tejto operácie sú dva vektory, výstup je reálne číslo.
Vďaka skalárnemu súčinu môžeme vypočítať napríklad aký uhol vektory zvierajú, špeciálne či sú na seba kolmé (v takom prípade ich skalárny súčin vyjde nulový).
HoreVektory: násobenie konštantou, súčet, rozdiel
Súčet vektorov
Vektory \vec{u} a \vec{v} sčítame takto: počiatočný bod vektora \vec{v} posunieme do koncového bodu vektora \vec{u}. Súčet vektorov \vec{u} a \vec{v} je vektor \vec{w}, ktorý má počiatočný bod rovnaký ako vektor \vec{u} a koncový bod rovnaký ako vektor \vec{v}. Píšeme: \vec{u}+\vec{v}=\vec{w}
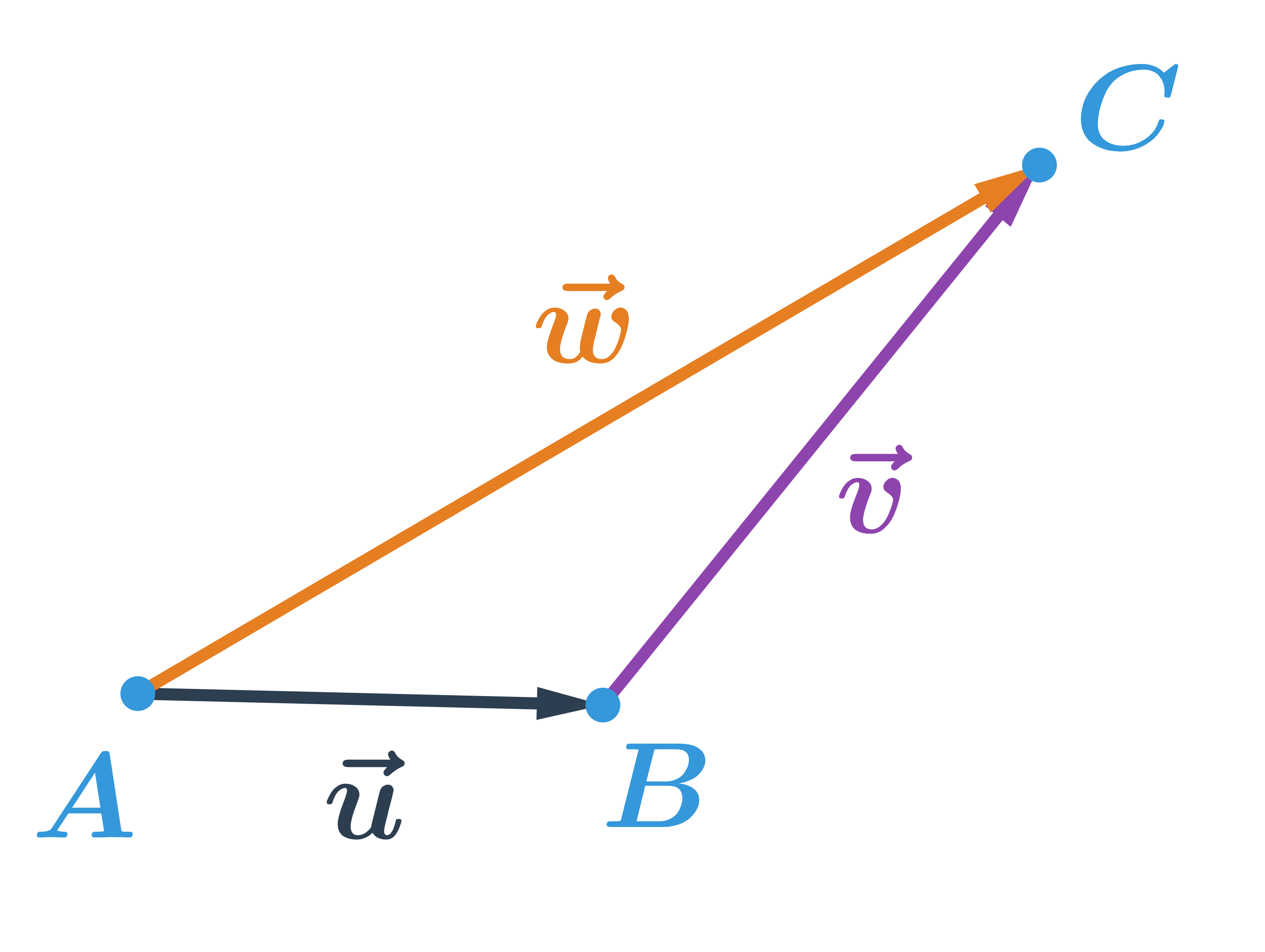
Vektory na obrázku sú označené \vec{u}=\overrightarrow{AB}, \vec{v}=\overrightarrow{BC}. Súčet týchto vektorov: \overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}
Majme vektory so súradnicami \vec{u}=(u_1;u_2), \vec{v}=(v_1;v_2). Potom súčet vektorov \vec{u} a \vec{v} je vektor \vec{w} so súradnicami \vec{w}=(u_1+v_1; u_2+v_2).
Rozdiel vektorov
Rozdiel vektorov \vec{u} a \vec{v} je súčet vektora \vec{u} s vektorom opačným k \vec{v}. Teda:
\vec{u}-\vec{v}=\vec{u}+(-\vec{v})
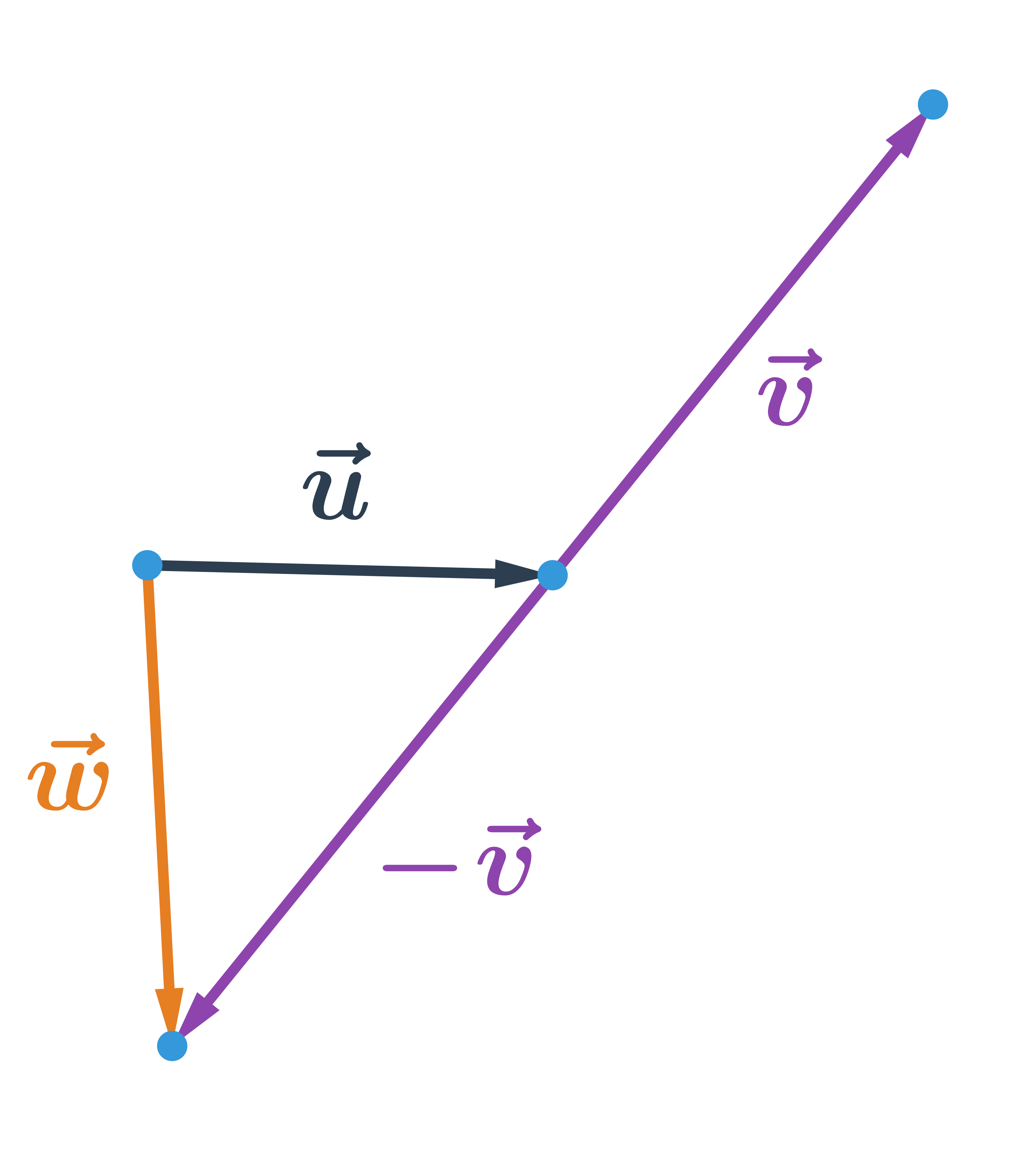
Ak máme súradnice vektorov: \vec{u}=(u_1;u_2), \vec{v}=(v_1;v_2), potom rozdiel vektorov \vec{u} a \vec{v} je vektor \vec{w}, ktorý má súradnice: \vec{w}=(u_1-v_1; u_2-v_2).
Násobok vektora
Vektor \vec{u} môžeme vynásobiť ľubovoľným reálnym číslom k. Dostaneme vektor \vec{v}, ktorému hovoríme násobok vektora. Píšeme \vec{v}=k \cdot \vec{u}
- Ak k > 0, vektory \vec{u} a k \cdot \vec{u} majú rovnaký smer
- Ak k < 0, vektory \vec{u} a k \cdot \vec{u} majú opačný smer
- Ak k = 0, vektor k \cdot \vec{u} je nulový vektor
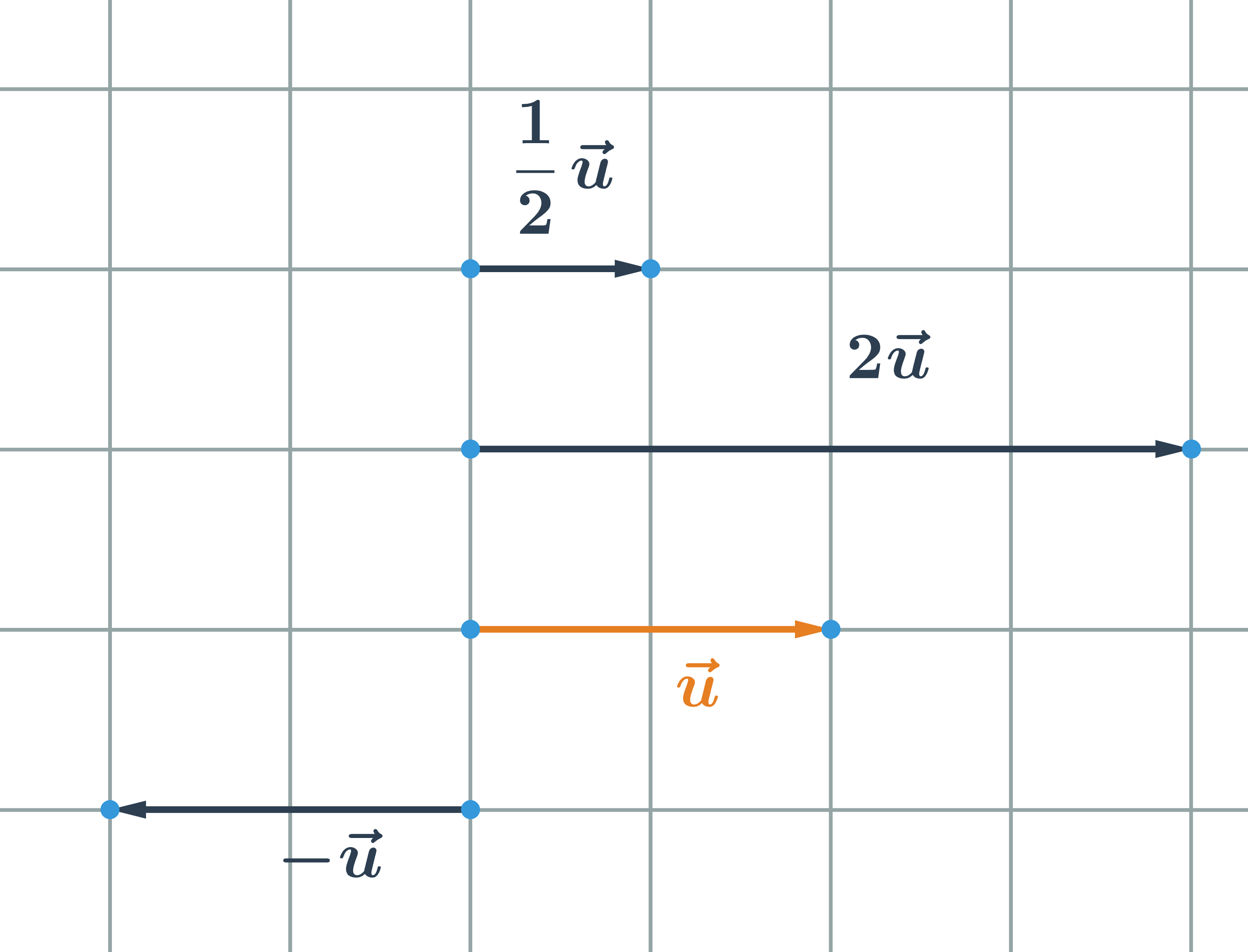
Ak máme súradnice vektora \vec{u}=(u_1;u_2), potom jeho násobok \vec{v}=k \cdot \vec{u} má súradnice \vec{v}=(k \cdot u_1; k\cdot u_2).
Príklad súčtu a násobku vektora graficky
Načrtnite vektor \vec{w}=2\vec{a}-\vec{b}+\vec{c}.
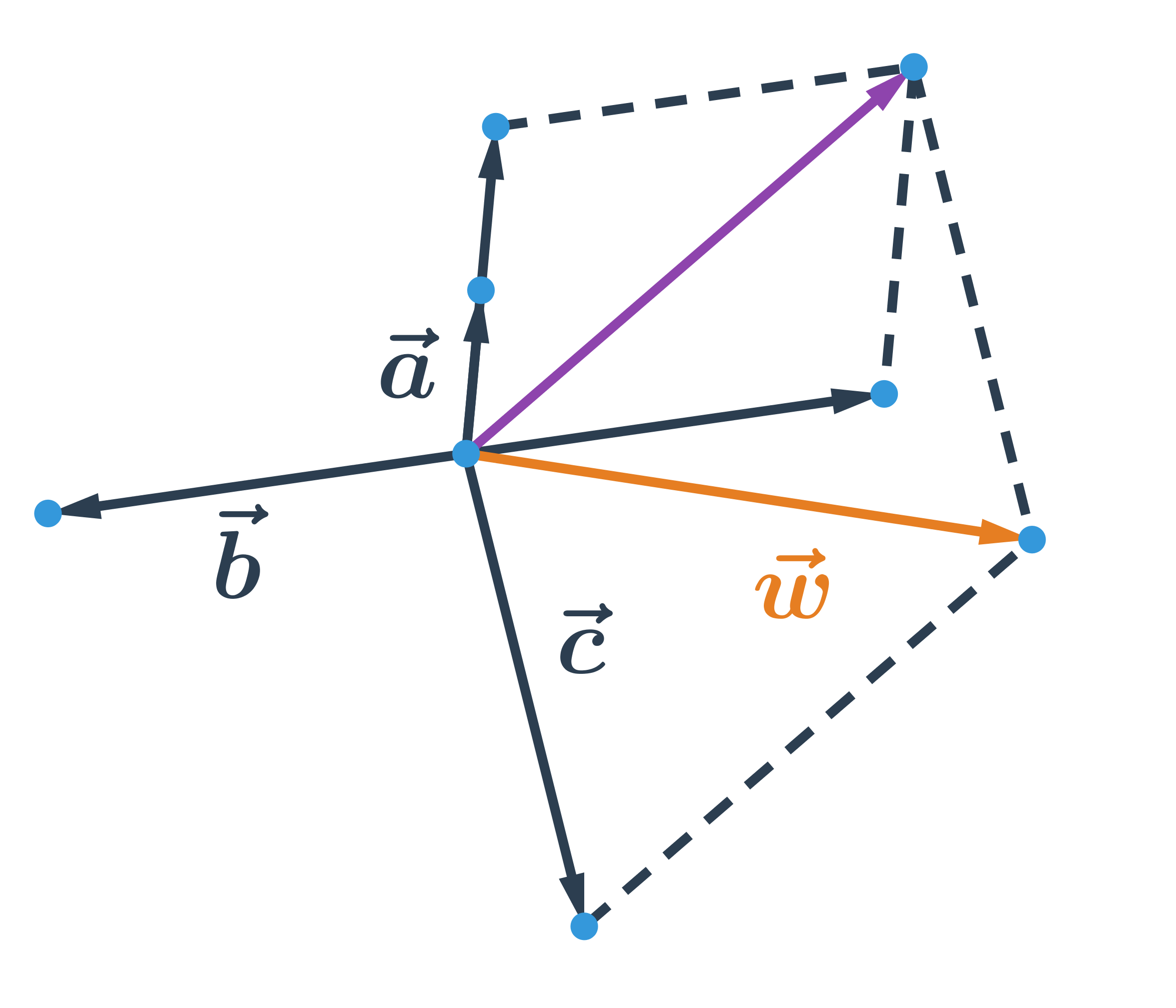
Príklad súčtu a násobku vektora v súradniciach
Sú dané vektory \vec{u}=(2;-3), \vec{v}=(4;1). Určite súradnice vektora \vec{w}=\vec{u}-4\cdot \vec{v}.
- w_1=u_1-4\cdot v_1=2-4\cdot 4=-14
- w_2=u_2-4\cdot v_2=-3-4\cdot 1=-7
Vektory: skalárny súčin
Skalárny súčin vektorov \vec{u} a \vec{v} označujeme \vec{u}\cdot \vec{v}. Pre vektory \vec{u}, \vec{v} s veľkosťami \left| \vec{u} \right| a \left| \vec{v} \right|, ktoré spolu zvierajú uhol \alpha, je skalárny súčin definovaný nasledovne:
\vec{u}\cdot \vec{v}=\left| \vec{u} \right|\cdot\left| \vec{v} \right|\cdot \cos \alpha
Vlastnosti skalárneho súčinu
- Výsledkom skalárneho súčinu dvoch vektorov je číslo (teda skalár).
- Skalárny súčin nulového vektora s ľubovoľným iným vektorom je vždy rovný 0.
- Skalárny súčin vektorov, ktoré sú na seba kolmé, je tiež rovný nule.
Výpočet pomocí súradníc
Ak máme súradnice vektorov \vec{u}=(u_1;u_2), \vec{v}=(v_1;v_2), potom hodnota ich skalárneho súčinu je:
u_1\cdot v_1+u_2 \cdot v_2
Poznámka: ďalšie typy súčinu vektorov
Okrem skalárneho súčinu existujú aj iné typy súčinu vektorov (vektorový, zmiešaný), preto je dôležité písať o aký súčin ide.Príklad: skalárny súčin vektorov
Určite skalárny súčin vektorov, ak platí: \left| \vec{u} \right|=4, \left| \vec{v} \right|=3 a vektory zvierajú uhol 60°.
- Vzorec: \vec{u}\cdot \vec{v}=\left| \vec{u} \right|\cdot\left| \vec{v} \right|\cdot \cos \alpha
- Dosadíme známe hodnoty: \vec{u}\cdot \vec{v}=4\cdot3\cdot \cos 60°=4\cdot3\cdot\frac{1}{2}=6
Určenie uhla zvieraného dvomi vektormi
S využitím vzťahu pre skalárny súčin môžeme určiť uhol vektorov: \cos \alpha=\frac{\vec{u}\cdot \vec{v}}{\left| \vec{u} \right|\cdot\left| \vec{v} \right|}
Príklad: uhol zvieraný vektormi
Určite uhol vektorov \vec{u}=(3;3) a \vec{v}=(2;0).
- Platí \cos \alpha=\frac{\vec{u}\cdot \vec{v}}{\left| \vec{u} \right|\cdot\left| \vec{v} \right|}.
- Pomocou známych súradníc vektorov vieme vypočítať skalárny súčin \vec{u}\cdot\vec{v} a veľkosti vektorov \left| \vec{u} \right|, \left| \vec{v} \right|:
- \vec{u}\cdot \vec{v}=u_1\cdot v_1+u_2 \cdot v_2=3\cdot2+3\cdot0=6
- \left| \vec{u} \right|=\sqrt{u_1^2 + u_2^2}=\sqrt{3^2+3^2}=\sqrt{18}
- \left| \vec{v} \right|=\sqrt{v_1^2 + v_2^2}=\sqrt{2^2+0^2}=\sqrt{4}
- Dosadíme tieto hodnoty do vzťahu pre výpočet \cos \alpha:
- \cos \alpha =\frac {6}{\sqrt{18}\cdot\sqrt{4}}=\frac{6}{3\sqrt{2}\cdot2}=\frac{1}{\sqrt{2}}
- Uhol vektorov je 60°.
Priamka je jednoznačne určená bodom, ktorý na nej leží, a smerovým vektorom, čo si môžete prakticky vyskúšať v kapitolke Určenie priamky.
V rovine aj v priestore sa dá zapísať priamku ako množinu bodov, ktoré spĺňajú parametrickú rovnicu. V rovine dokážeme pre danú priamku napísať tiež všeobecnú rovnicu (ale v priestore nie).
Ak máme priamku popísanú rovnicou, dokážeme určiť vzájomnú polohu dvoch priamok alebo vzájomnú polohu priamky a bodu výpočtom.
HorePriamky: pojmy
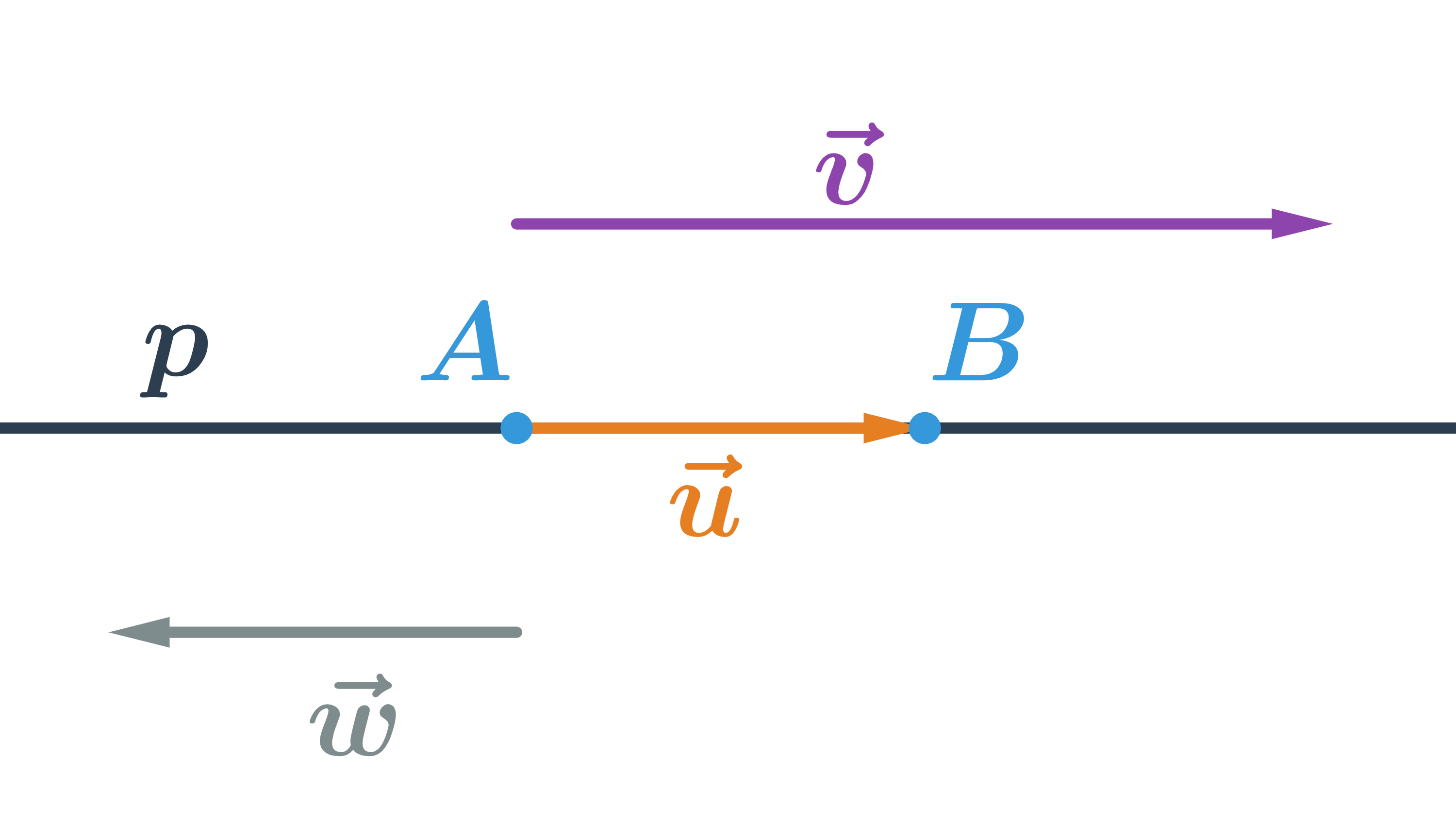
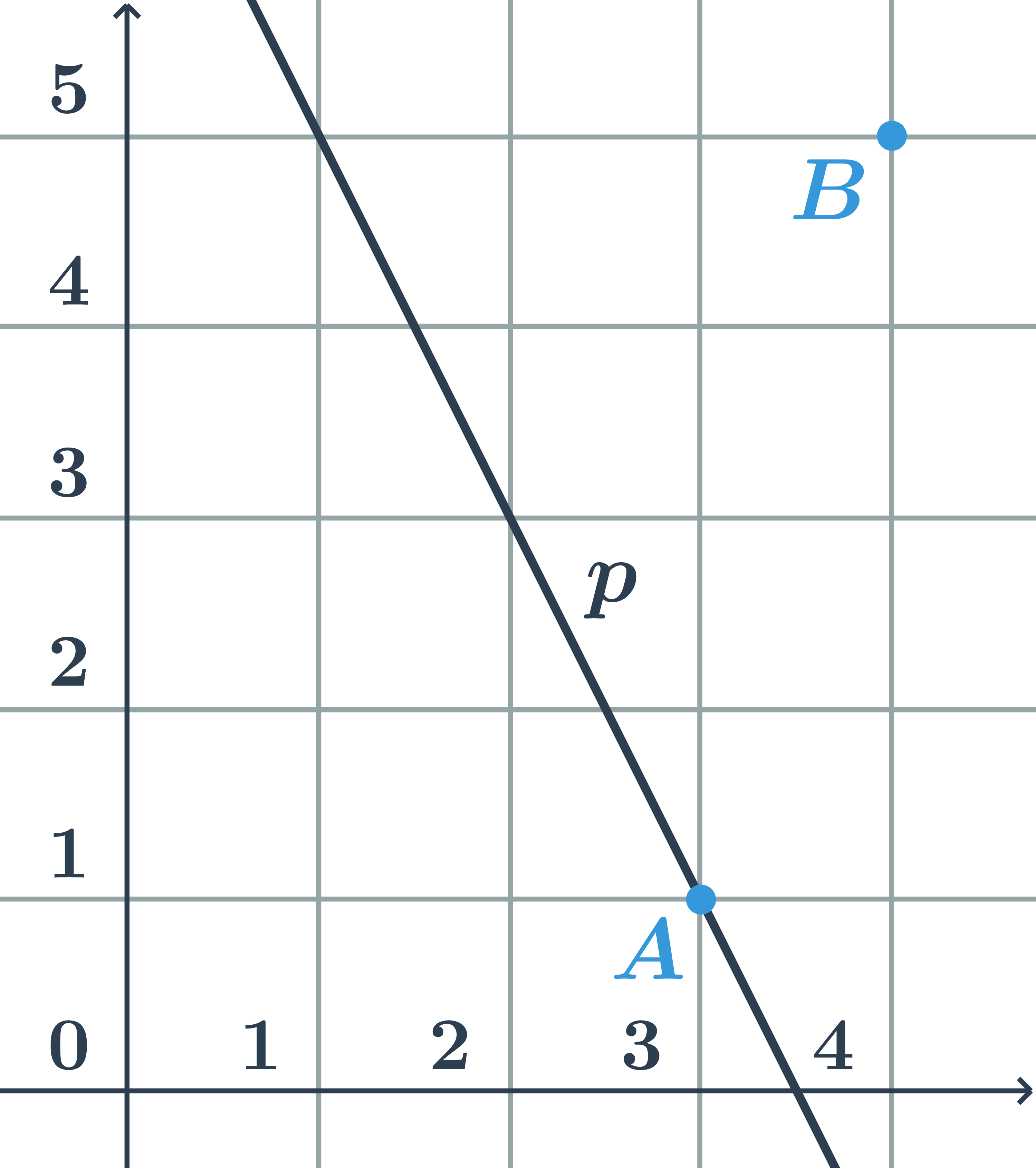
Priamka je jednoznačne určená dvomi bodmi, na obrázku je priamka p určená bodmi A a B. Každý vektor, ktorý je rovnobežný s vektorom \overrightarrow{AB} sa nazýva smerový vektor priamky p. Ktorýkoľvek z vektorov na obrázku je smerový vektor priamky p. K tomu, aby sme určili konkrétnu priamku ešte potrebujeme poznať jeden bod na priamke (priamka p na obrázku je určená bodom A a ktorýmkoľvek z vektorov \vec{u}, \vec{v}, \vec{w}).
Parametrické rovnice priamky
Priamka určená bodom A=[a_1;a_2] a vektorom \vec{u}=(u_1;u_2) má parametrické rovnice tvaru: \begin{array}{rrl}x&=&a_1+t\cdot u_1\\y&=&a_2+t\cdot u_2\\&&t\in\mathbb{R}\end{array} Skrátene môžeme vyjadriť p:X=A+t\vec{u}, číslo t nazývame parameter.
Ako súvisí hodnota parametra t s polohou bodu na priamke
- Priamka p je určená bodom A a vektorom \vec{u}=\overrightarrow{AB}, teda p:X=A+t\vec{u}
- Pre hodnotu t=0 dostaneme: X=A+t\vec{u}=A+0\cdot \vec{u} … bod A
- Pre hodnotu t=1 dostaneme: X=A+t\vec{u}=A+1\cdot \vec {u} … bod B
- Pre hodnotu t=2 dostaneme: X=A+t\vec{u}=A+2\cdot \vec {u} … bod C
- Pre hodnotu t=\frac{1}{2} dostaneme: X=A+t\vec{u}=A+\frac{1}{2}\cdot \vec{u} … bod D (stred úsečky AB)
- Pre hodnotu t=-1 dostaneme: X=A+t\vec{u}=A-1\cdot \vec{u} … bod E
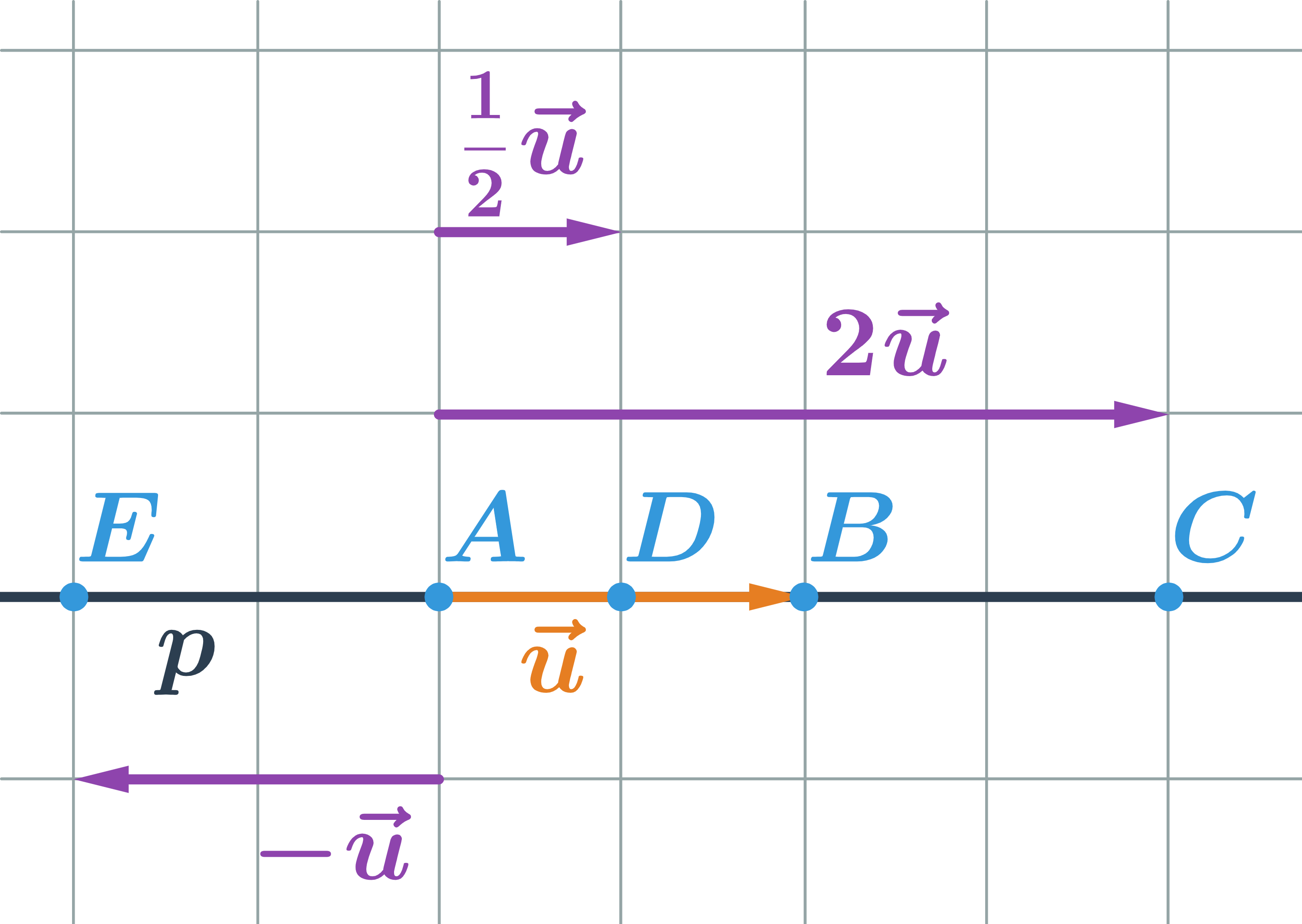
- Každá hodnota parametra určuje jeden bod na priamke, na určenie celej priamky teda potrebujeme všetky reálne čísla, preto píšeme t\in\mathbb{R}.
- Body, ktoré ležia na úsečke AB (teda body ležiace medzi bodmi A a B), vyjadríme parametricky, ak do rovnice X=A+t\vec{u} dosadíme hodnoty parametra t spĺňajúce 0\leq t\leq1.
Všeobecná rovnica priamky
Každý vektor kolmý k priamke p sa nazýva normálový vektor priamky p. Všeobecná rovnica priamky je rovnica v tvare: ax+by+c=0, kde konštanty a a b sú súradnice normálového vektora a c reálne číslo.
Súradnice smerového a normálového vektora priamky p
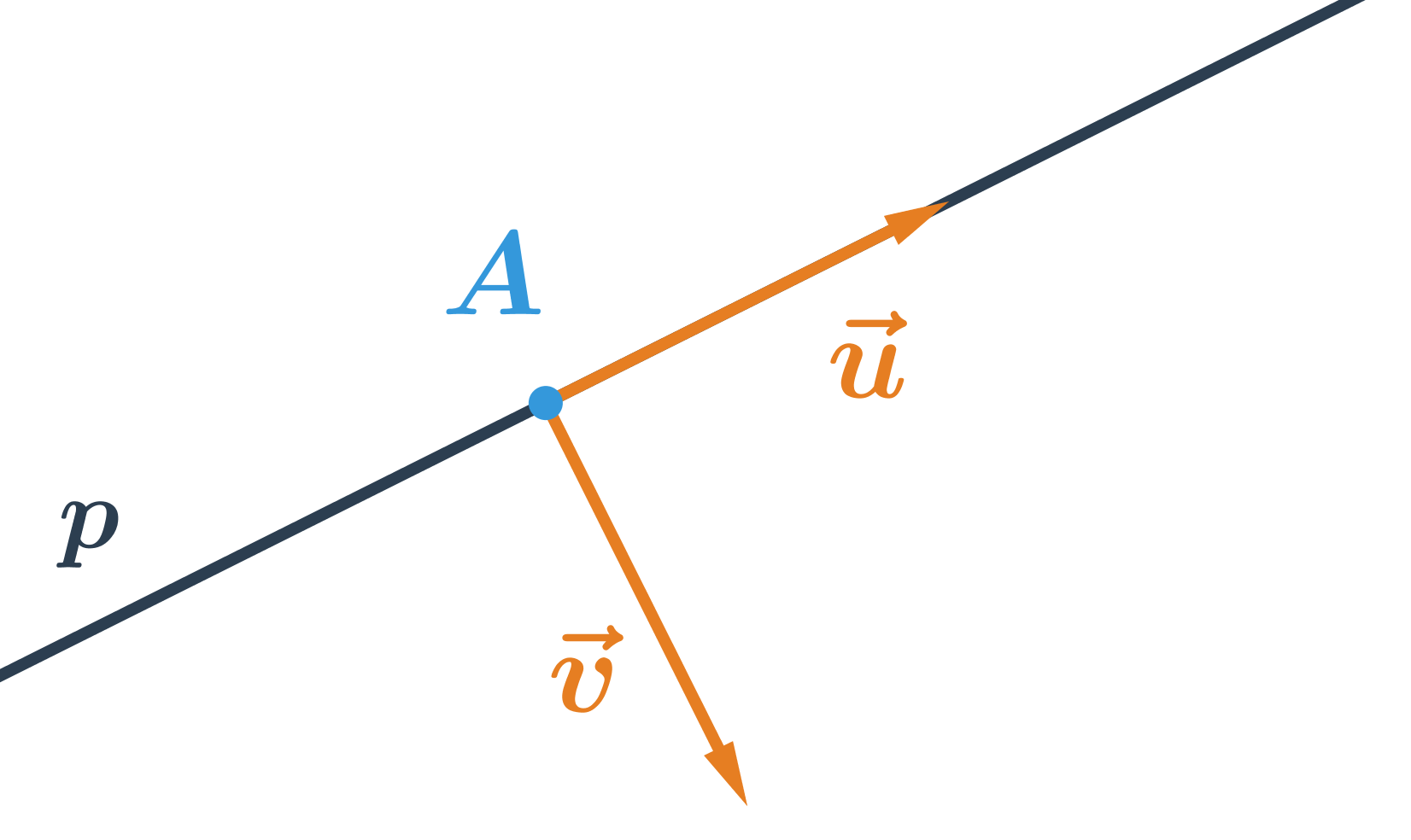
- Pre priamku danú všeobecnou rovnicou ax+by+c=0:
- \vec{v} je normálový vektor priamky p, jeho súradnice sú: \vec{v}=(a;b)
- \vec{u} je smerový vektor priamky p, pretože je to vektor kolmý na vektor \vec{v}=(a;b), jeho súradnice sú: \vec{u}=(-b;a)
- Pre priamku danú parametricky: \begin{array}{rrl}x&=&a_1+t\cdot u_1\\y&=&a_2+t\cdot u_2\\&&t\in\mathbb{R}\end{array}
- \vec{u} je smerový vektor priamky p, jeho súradnice sú: \vec{u}=(u_1;u_2)
- \vec{v} je normálový vektor priamky p, pretože je to vektor kolmý na vektor \vec{u}=(u_1;u_2), jeho súradnice sú: \vec{v}=(-u_2;u_1)
Všeobecná rovnica priamky rovnobežnej s osou x
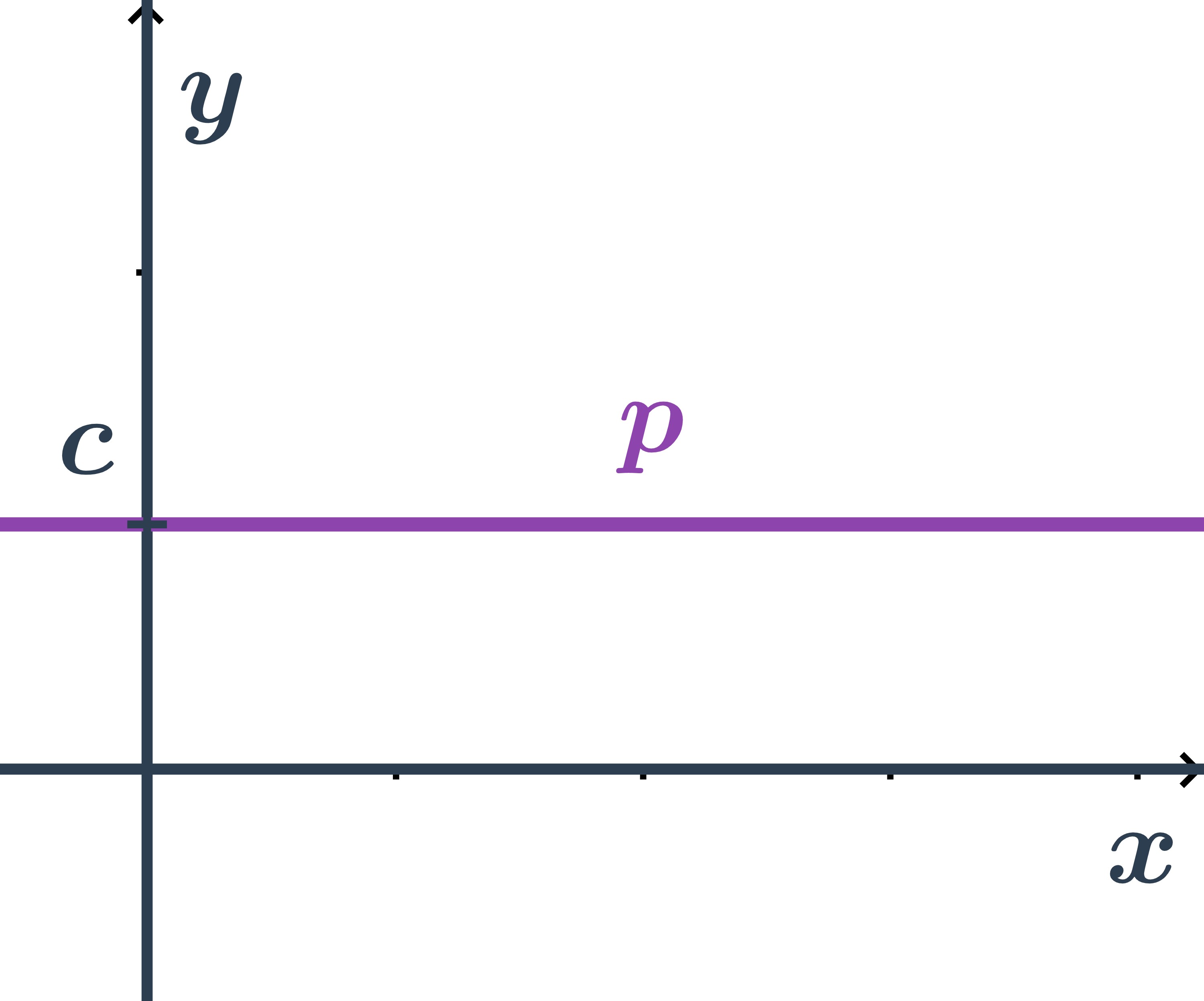
- Pre všetky body ležiace na priamke je druhá súradnica rovnaká a to: y=c
- Teda priamka má všeobecnú rovnicu: y-c=0
Všeobecná rovnica priamky rovnobežnej s osou y
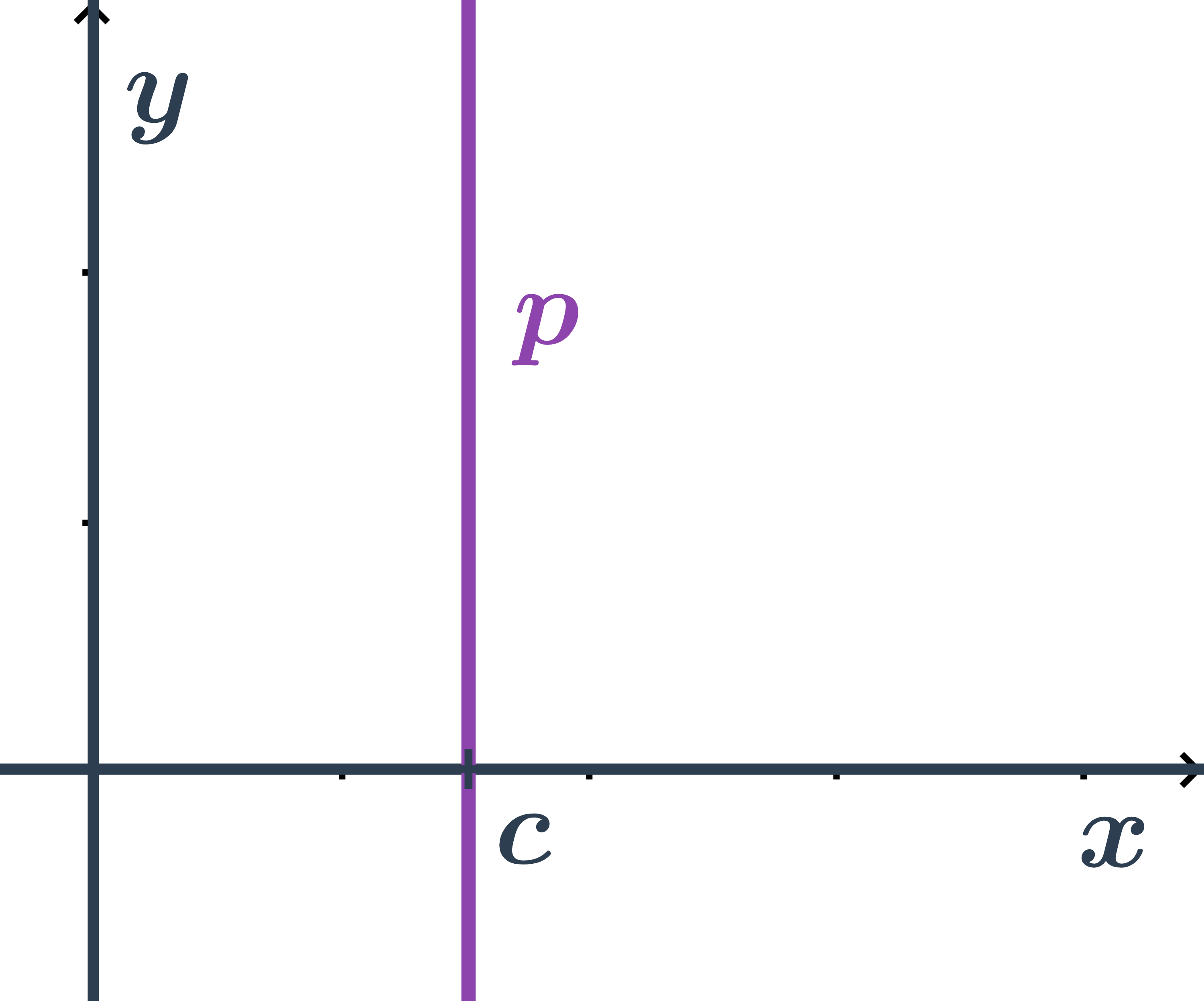
- Pre všetky body ležiace na priamke je prvá súradnica rovnaká a to: x=c
- Teda priamka má všeobecnú rovnicu: x-c=0
Bod a priamka
Bod M=[m_1;m_2] leží na priamke, ak jeho súradnice vyhovujú rovnici priamky. Ak je priamka daná všeobecnou rovnicou ax+by+c=0, pre súradnice bodu, ktorý leží na priamke platí: a\cdot m_1+b\cdot m_2+c=0. Ak je priamka daná parametricky, po dosiahnutí súradníc bodu vychádza z oboch rovníc rovnaká hodnota parametra t. (Viac o vzájomnej polohe bodu a priamky.)
Všeobecná rovnica priamky, ktorá prechádza počiatkom
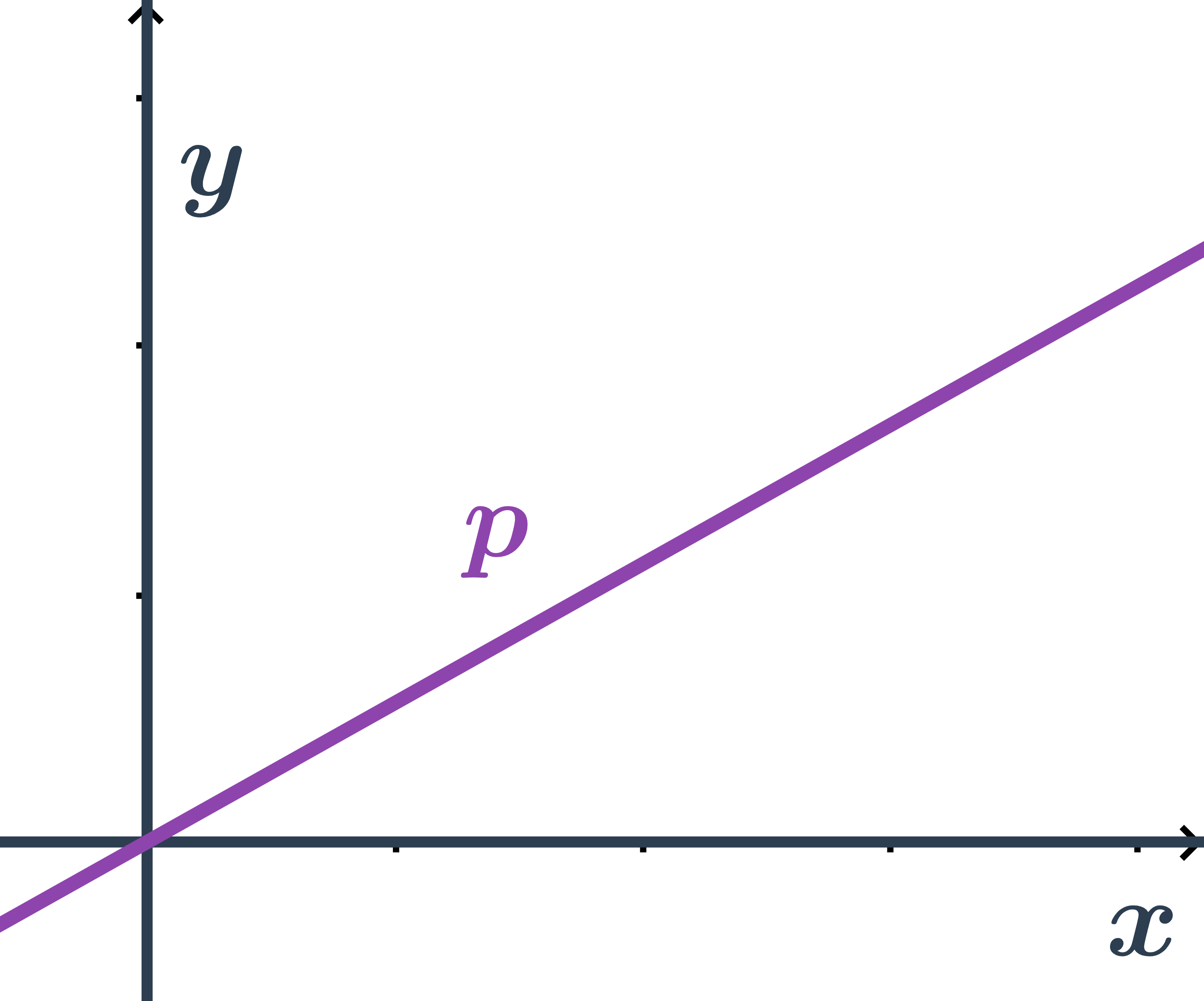
- Priamka prechádza bodom O=[0;0], teda súradnice počiatku spĺňajú jej všeobecnú rovnicu ax+by+c=0.
- Dosadíme súradnice bodu O a skúsime zistiť nejaké informácie o konštantách a,b,c.
- a\cdot0+b\cdot0+c=0\Leftrightarrow c=0
- Preto má priamka, ktorá prechádza počiatkom, všeobecnú rovnicu ax+by=0.
Dve priamky
Priamky rovnobežné majú rovnaký smer, teda ich smerové vektory sú kolineárne. Normálové vektory dvoch rovnobežných priamok sú tiež kolineárne. V špeciálnom prípade môžu byť priamky totožné.
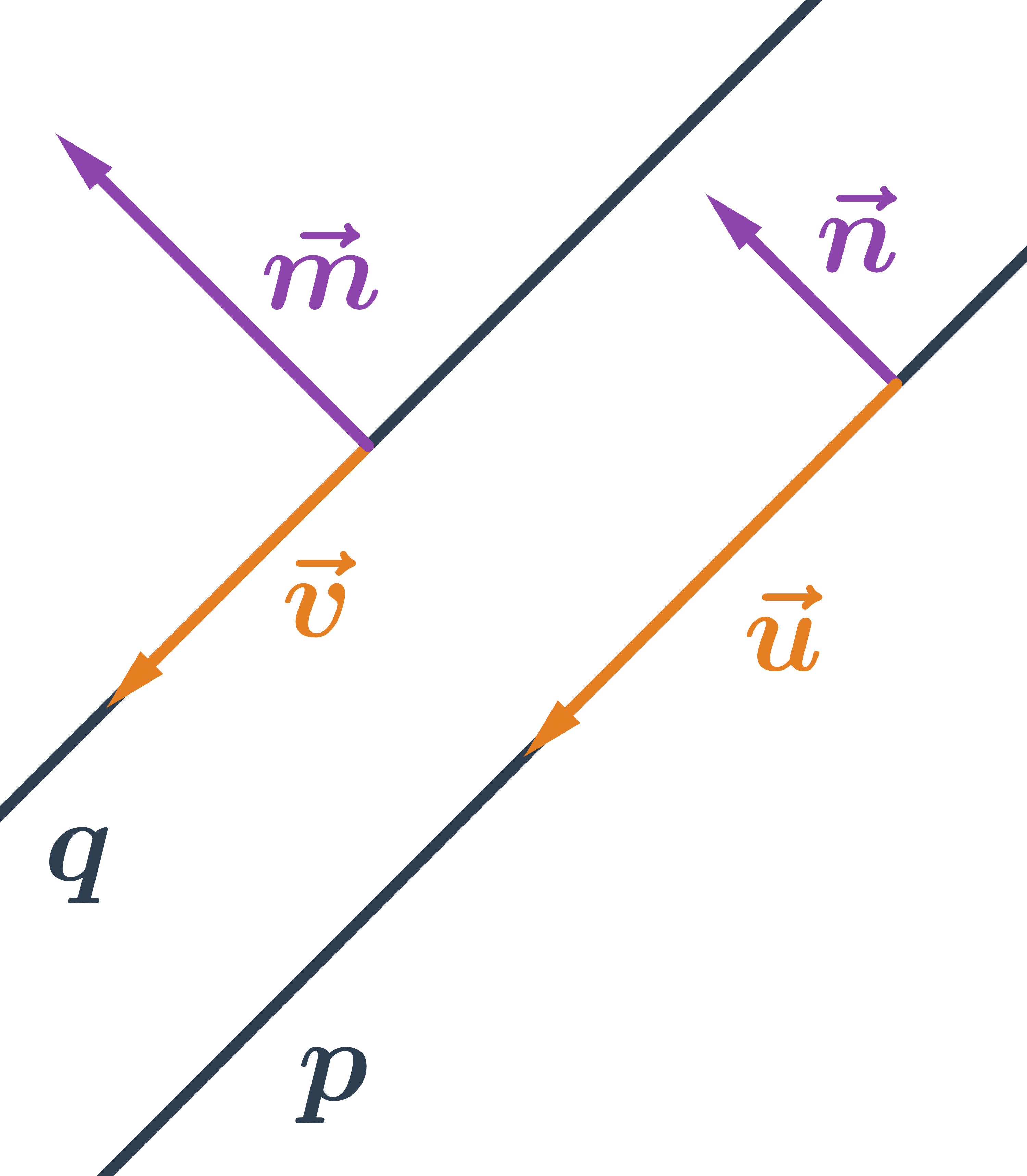
Priamky rôznobežné majú jeden spoločný bod, tento bod musí spĺňať rovnice oboch priamok. Ich smerové vektory nie sú kolineárne, normálové vektory tiež nie sú kolineárne.
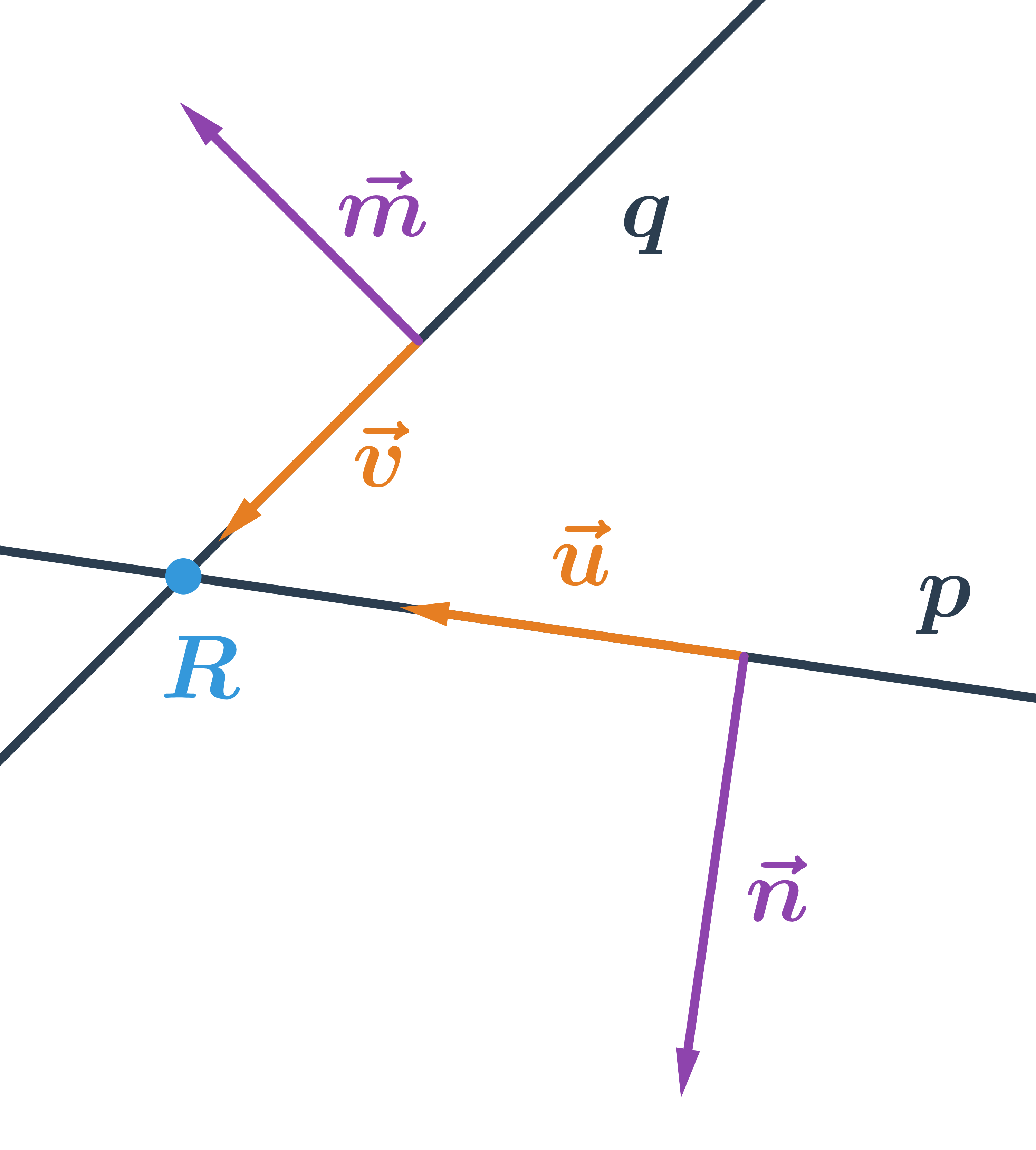
Viac o vzájomnej polohe dvoch priamok.
Priamka v priestore
Priamku v priestore nie je možné vyjadriť všeobecnou rovnicou. Parametrickú rovnicu priamky v priestore určíme podobne ako v rovine na základe znalosti súradníc smerového vektora a jedného bodu na priamke.
HoreUrčenie priamky
Priamka je väčšinou určená bodom a vektorom, prípadne dvomi bodmi.
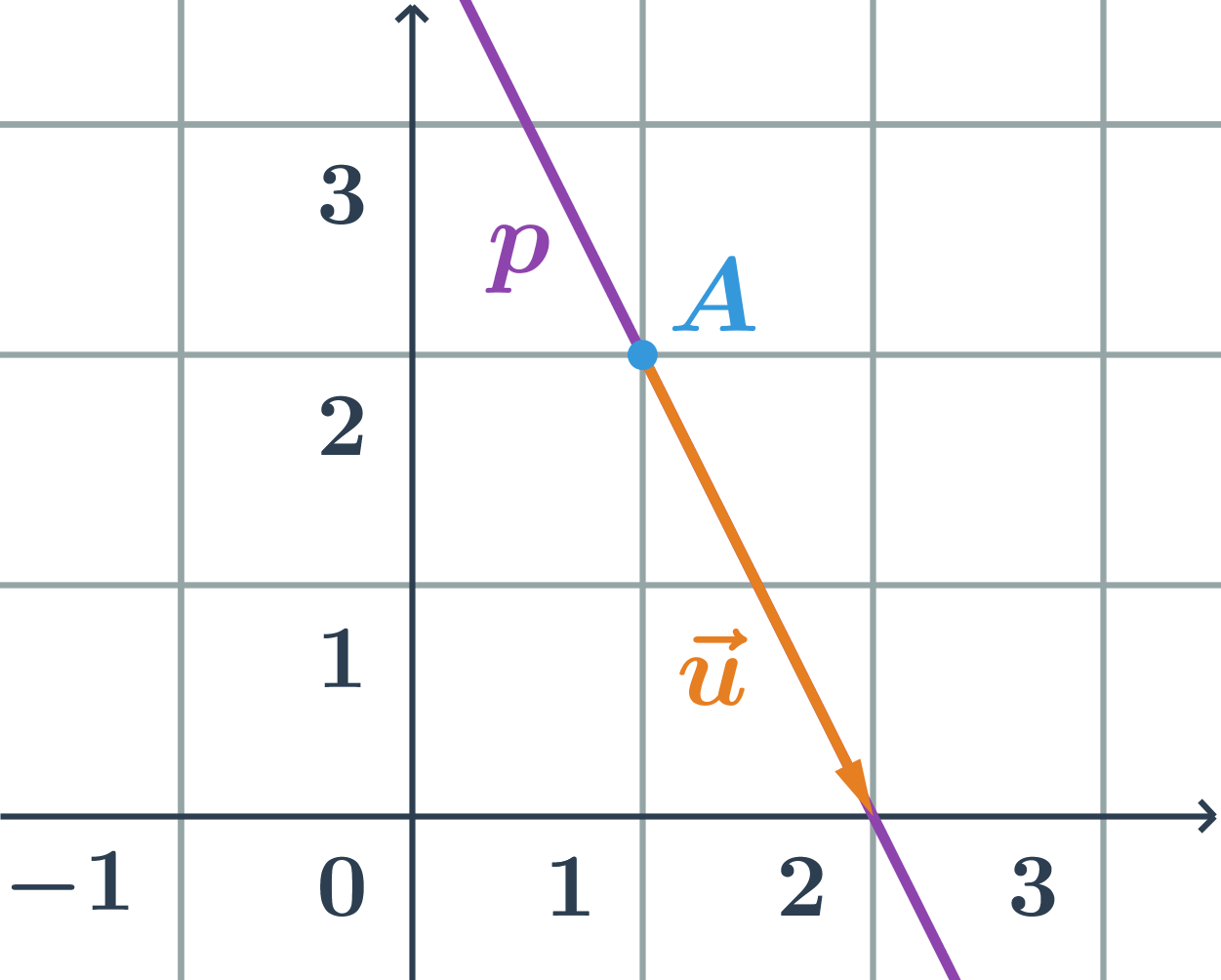
Priamka p na obrázku je určená napríklad:
- bodom A=[1;2], ktorý na nej leží a smerovým vektorom \vec{u}=(1;-2)
- alebo dvomi rôznymi bodmi [1;2] a [2;0], ktoré na nej ležia
Parametrické rovnice priamky v rovine
Priamka určená bodom A=[a_1;a_2] a smerovým vektorom \vec{u}=(u_1;u_2) má parametrické rovnice tvaru:
\begin{array}{rrl}x&=&a_1+t\cdot u_1\\y&=&a_2+t\cdot u_2\\&&t\in\mathbb{R}\end{array}
Skrátene môžeme vyjadriť p:X=A+t\vec{u}, číslo t nazývame parameter. Ak poznáme dva body A, B ležiace na priamke, smerový vektor je napríklad \vec{u}=\overrightarrow{AB}.
Parametrické rovnice priamky p určenej bodmi A=[1;2] a B=[3;1]
- priamka p je určená bodom A a smerovým vektorom \vec{u}=\overrightarrow{AB}=B-A=(2;-1)
- parametrické rovnice priamky p: \begin{array}{rrl}x&=&1+2t\\y&=&2-t\\&&t\in\mathbb{R}\end{array}
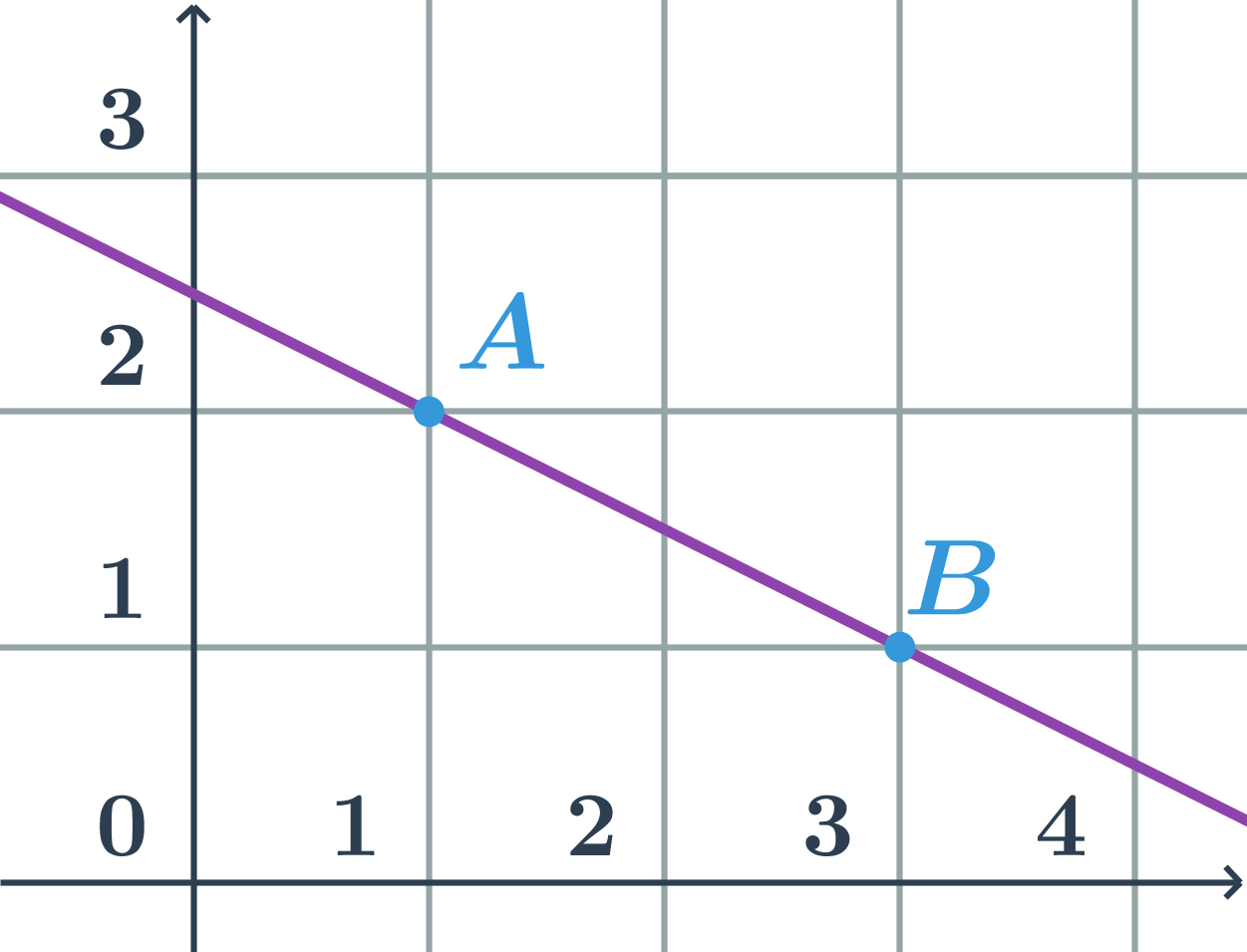
Rôzne parametrické rovnice priamky na obrázku
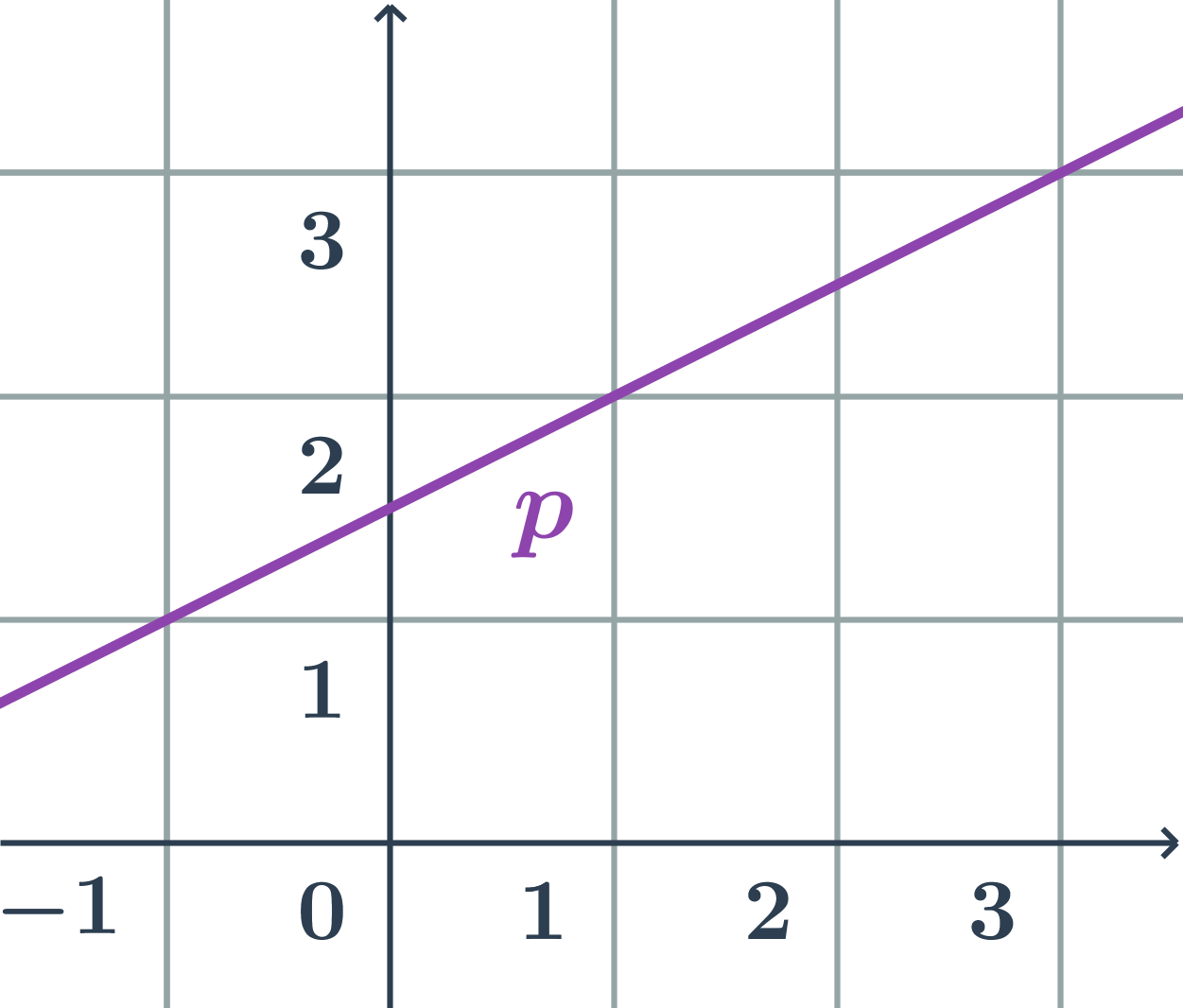
Určíme súradnice smerového vektora a jedného bodu na priamke:
- napríklad: \vec{u}=(2;1), A=[1;2]
- parametrické rovnice priamky p: \begin{array}{rrl}x&=&1+2t\\y&=&2+t\\&&t\in\mathbb{R}\end{array}
Ďalšia možnosť parametrického vyjadrenia:
- \vec{v}=(-4;-2), B=[3;3]
- parametrické rovnice priamky p: \begin{array}{rrl}x&=&3-4t\\y&=&3-2t\\&&t\in\mathbb{R}\end{array}
Na určenie parametrických rovníc môžeme vybrať ktorýkoľvek bod ležiaci na priamke a akýkoľvek zápis súradníc smerového vektora, možností ako parametricky vyjadriť danú priamku je teda nekonečne veľa.
Všeobecná rovnica priamky v rovine
Všeobecná rovnica priamky v rovine má tvar: ax+by+c=0, kde konštanty a a b sú súradnice normálového vektora a c reálne číslo. Normálový vektor \vec{n}=(a;b) je vektor kolmý na danú priamku, teda aj kolmý na smerový vektor priamky.
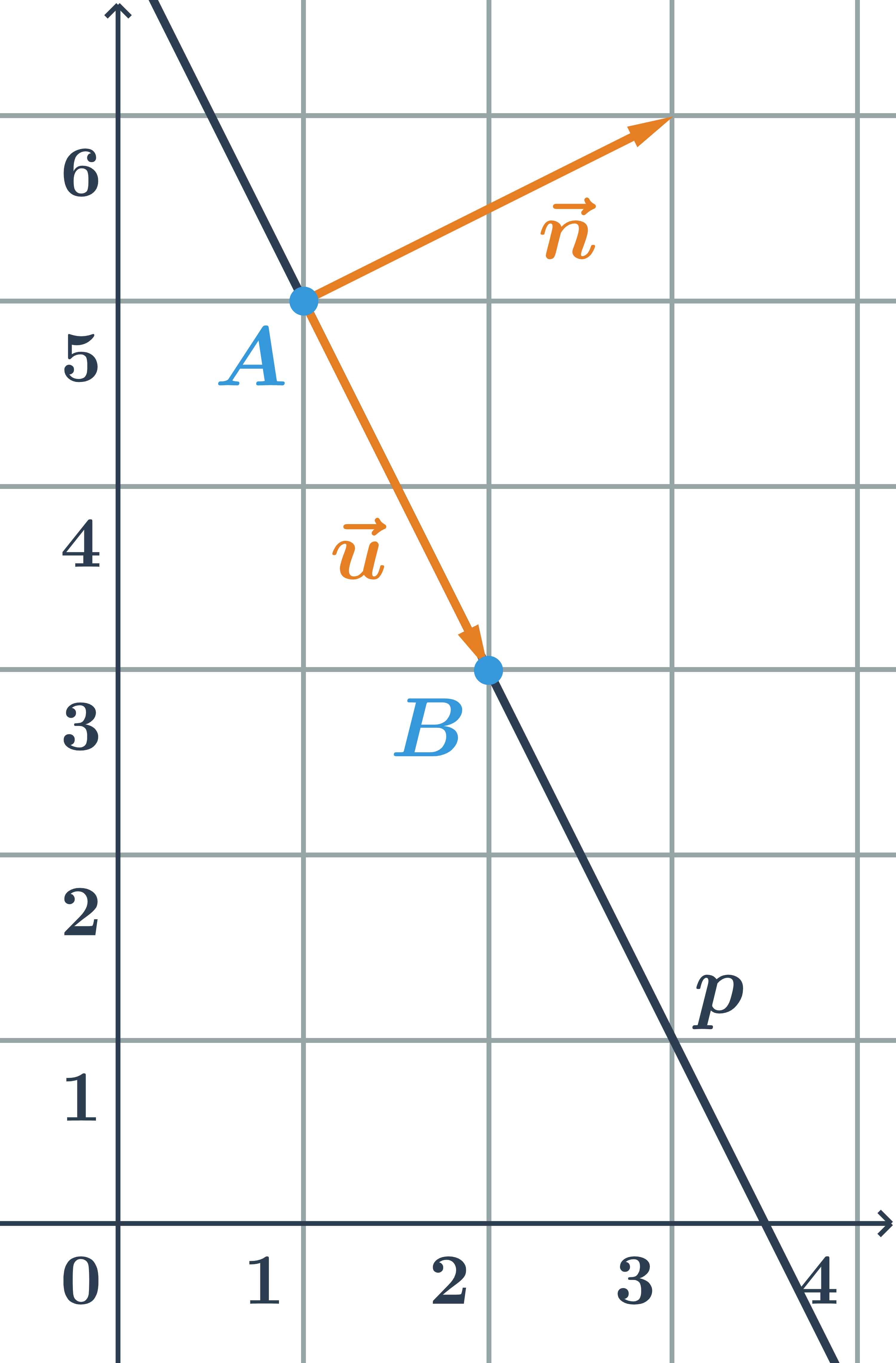
Všeobecná rovnica priamky p určené body A=[1;5] a B=[2;3]
- Priamka p je určená bodom A a smerovým vektorom \vec{u}=\overrightarrow{AB}=B-A=(1;-2).
- Normálový vektor je kolmý na vektor \vec{u}=(1;-2), teda napríklad vektor \vec{n}=(2;1).
- Súradnice normálového vektoru sú konštanty a a b vo všeobecnej rovnici priamky. Všeobecná rovnica má tvar: 2x+y+c=0
- Konštantu c dopočítame dosadením súradníc bodu A=[1;5] :
- 2\cdot1+5+c=0\Rightarrow c=-7
- Všeobecná rovnica priamky p je: 2x+y-7=0
Všeobecná rovnica priamky danej parametricky
Určite všeobecnú rovnicu priamky p, ktorá je daná nasledujúcou parametrickou sústavou rovníc: \begin{array}{rrl}x&=&1+2t\\y&=&4+6t\\&&t\in\mathbb{R}\end{array}
- Priamka p je určená bodom A=[1;4] a smerovým vektorom \vec{u}=(2;6).
- Súradnice smerového vektora môžeme upraviť na tvar: \vec{u}=(1;3).
- Normálový vektor je kolmý na vektor \vec{u}=(1;3), teda napríklad vektor \vec{n}=(3;-1).
- Súradnice normálového vektora sú konštanty a a b vo všeobecnej rovnici priamky. Všeobecná rovnica má tvar: 3x-y+c=0
- Konštantu c dopočítame dosadením súradníc bodu A=[1;4] :
- 3\cdot1-4+c=0\Rightarrow c=1
- Všeobecná rovnica priamky p je: 3x-y+1=0
Parametrické vyjadrenie priamky danej všeobecnou rovnicou
Určite parametrické vyjadrenie priamky p, ktorá má všeobecnú rovnicu: 3x-2y+4=0.
- Priamka p má normálový vektor \vec{n}=(3;-2).
- Smerový vektor je kolmý na vektor \vec{n}=(3;-2), teda napríklad vektor \vec{u}=(2;3).
- Určíme jeden bod na priamke p : jednu súradnicu môžeme zvoliť, napríklad x=0, druhú súradnicu dopočítame: 3\cdot0-2y+4=0\Rightarrow y=2
- Zo všeobecnej rovnice sme teda zistili, že na priamke leží bod A=[0;2].
- Parametrické vyjadrenie priamky p je: \begin{array}{rrl}x&=&0+3t\\y&=&2-2t\\&&t\in\mathbb{R}\end{array}
Smernicový tvar rovnice priamky
Každú priamku p, ktorá nie je rovnobežná s osou y môžeme vyjadriť v tvare: y=kx+q, kde k,q\in\mathbb{R}.
Tento tvar sa nazýva smernicový tvar rovnice priamky.
Konštanta k sa nazýva smernica a jej hodnota je tangens uhla, ktorý zviera priamka p s kladnou časťou osi x, teda: k=\tan \varphi.
Konštanta q určuje priesečník priamky p s osou y, súradnice priesečníka sú: P=[0;q]. Pre priamku, ktorá prechádza počiatkom je q=0, teda smernicový tvar jej rovnice je: y=kx.
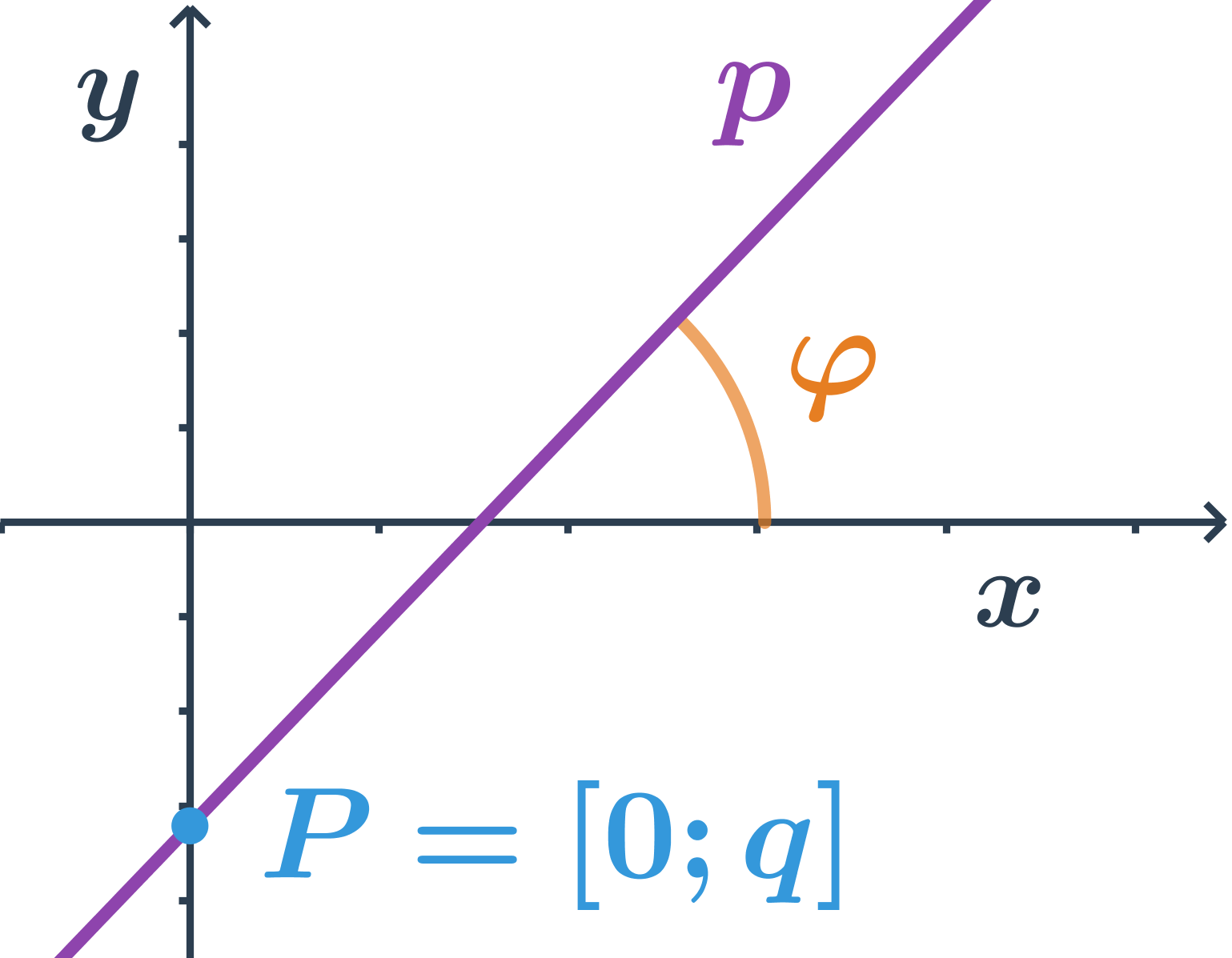
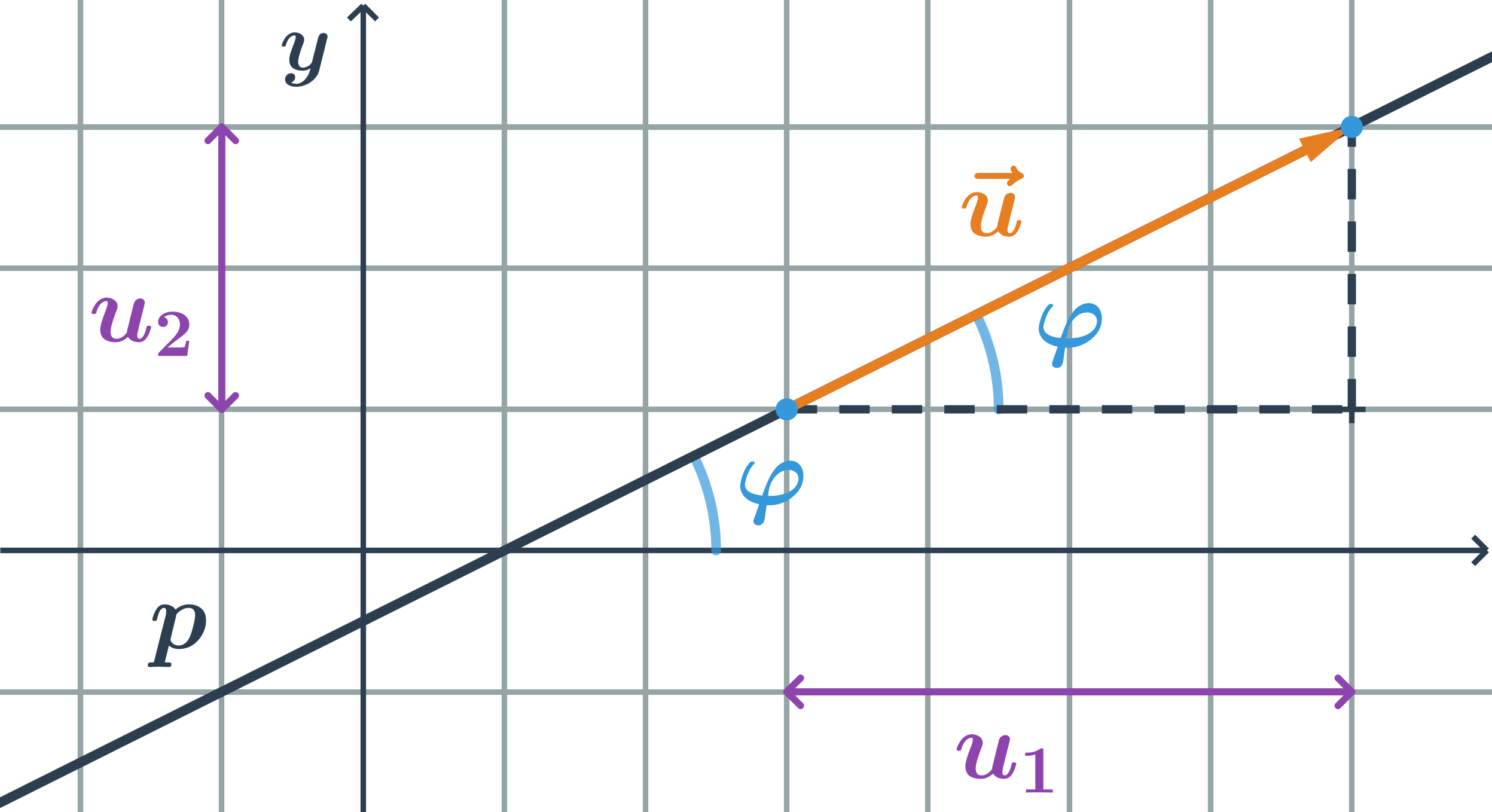
Smernica priamky, ktorá má smerový vektor \vec{u}=(u_1;u_2) je podiel súradnic smerového vektora:
k=\tan \varphi=\frac{u_2}{u_1}
Rôzne hodnoty smernice
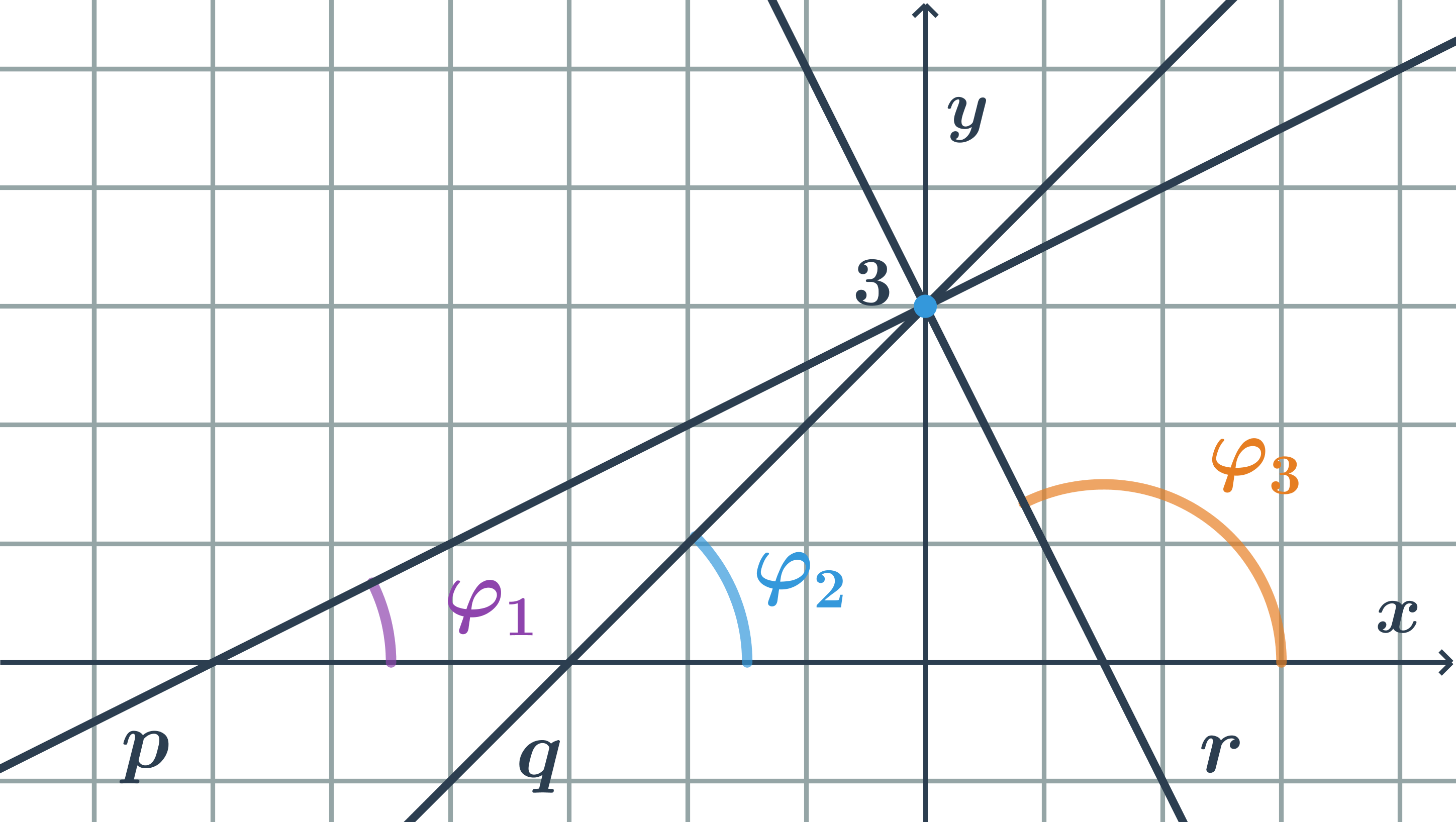
- Smernica priamky p: k_1=\tan \varphi_1=\frac{1}{2}
- Smernica priamky q: k_2=\tan \varphi_2=\frac{1}{1}=1
- Smernica priamky r: k_3=\tan \varphi_3=\frac{2}{1}=2
- Čím väčšia odchýlka od kladnej časti osi x, tým väčšia hodnota smernice k.
- Priamka rovnobežná s osou x zviera s kladnou časťou osi x uhol 0^\circ a teda jej smernica je \tan 0^\circ=0.
- Priamka rovnobežná s osou y zviera s kladnou časťou osi x uhol 90^\circ a pre túto hodnotu funkcie tangens nie je definovaná, preto nemôžeme určiť smernicu.
Smernicový tvar priamky z obrázka
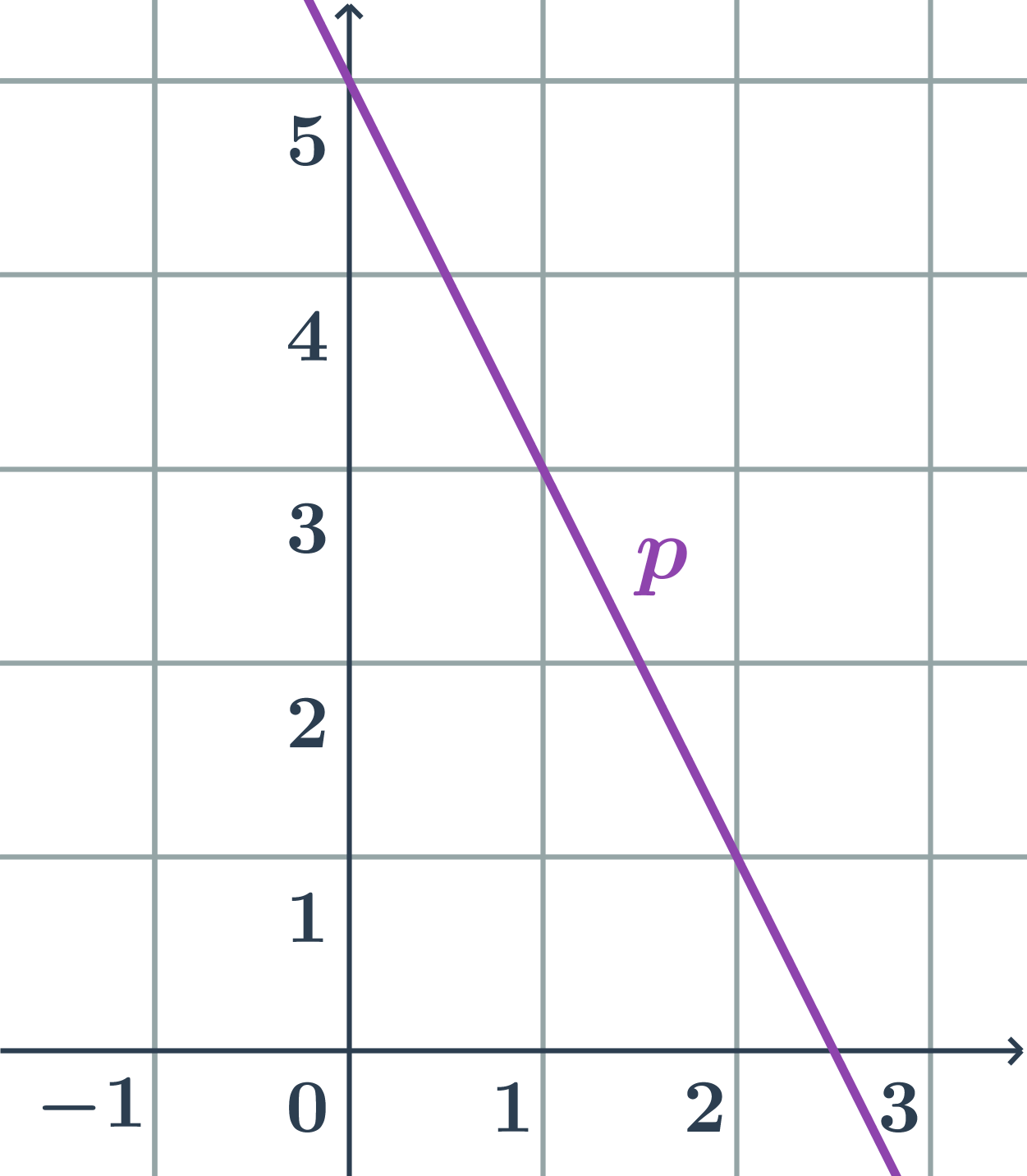
Hľadáme smernicový tvar rovnice priamky: y=kx+q.
- Pre nájdenie konštánt k a q určíme smerový vektor priamky p a priesečník s osou y.
- smerový vektor priamky: \vec{u}=(1;-2)
- smernica: k=\tan \varphi=\frac{u_2}{u_1}=\frac{-2}{1}=-2
- priesečník priamky s osou y: P=[0;5]
- konštanta q=y_P=5
- priamka na obrázku má smernicový tvar y=-2x+5
Dve priamky
Dve rovnobežné priamky zvierajú s kladnou časťou osi x rovnaký uhol, majú teda rovnakú smernicu.
Pre dve na seba kolmé priamky platí:
- priamka p má smerový vektor \vec{u}=(u_1;u_2) a teda smernicu: k=\frac{u_2}{u_1}
- každá priamka na ňu kolmá má smerový vektor (-u_2;u_1) a teda smernicu: \frac{-u_2}{u_1}=-\frac{1}{k}
Vzájomná poloha priamok v rovine
Vzájomnú polohu dvoch priamok môžeme ľahko určiť, ak poznáme súradnice ich smerových, prípadne normálových vektorov. Rovnobežne priamky majú rovnaký smer, teda ich smerové vektory sú kolineárne. Normálové vektory dvoch rovnobežných priamok sú tiež kolineárne. V špeciálnom prípade môžu byť priamky totožné. Rôznobežné priamky majú jeden spoločný bod, tento bod musí spĺňať rovnice oboch priamok. Ich smerové vektory nie sú kolineárne, normálové vektory tiež nie sú kolineárne.
Rovnobežky zadané parametrickými rovnicami
Určite vzájomnú polohu dvoch priamok p, q zadaných parametricky:
p: \begin{array}{rrl}x&=&-3+3t\\y&=&\hspace{0.25cm}2+t\\&&\hspace{0.25cm}t\in\mathbb{R}\end{array} \hspace{0.5cm}q: \begin{array}{rrl}x&=&1-3s\\y&=&2-s\\&&s\in\mathbb{R}\end{array}
- smerový vektor priamky p:\hspace{0.25cm}\vec{u}=(3;1)
- smerový vektor priamky q:\hspace{0.25cm}\vec{v}=(-3;-1)
- Priamky p a q sú rovnobežné, pretože ich smerové vektory sú kolineárne.
- Overíme, že priamky nie sú totožné. Stačí určiť, či bod, ktorý leží na jednej priamke neleží na priamke druhej.
- Na priamke p leží napríklad bod A=[-3;2].
- Overíme, že tento bod neleží na priamke q dosadením súradníc bodu A do rovníc priamky q: \begin{array}{rrl}-3&=&1-3s \Rightarrow s=\frac{4}{3}\\2&=&2-\hspace{0.15cm}s\Rightarrow s=0\end{array}
- Vyšli rôzne hodnoty parametra s, takže bod A neleží na q \Rightarrow priamky nie sú totožné
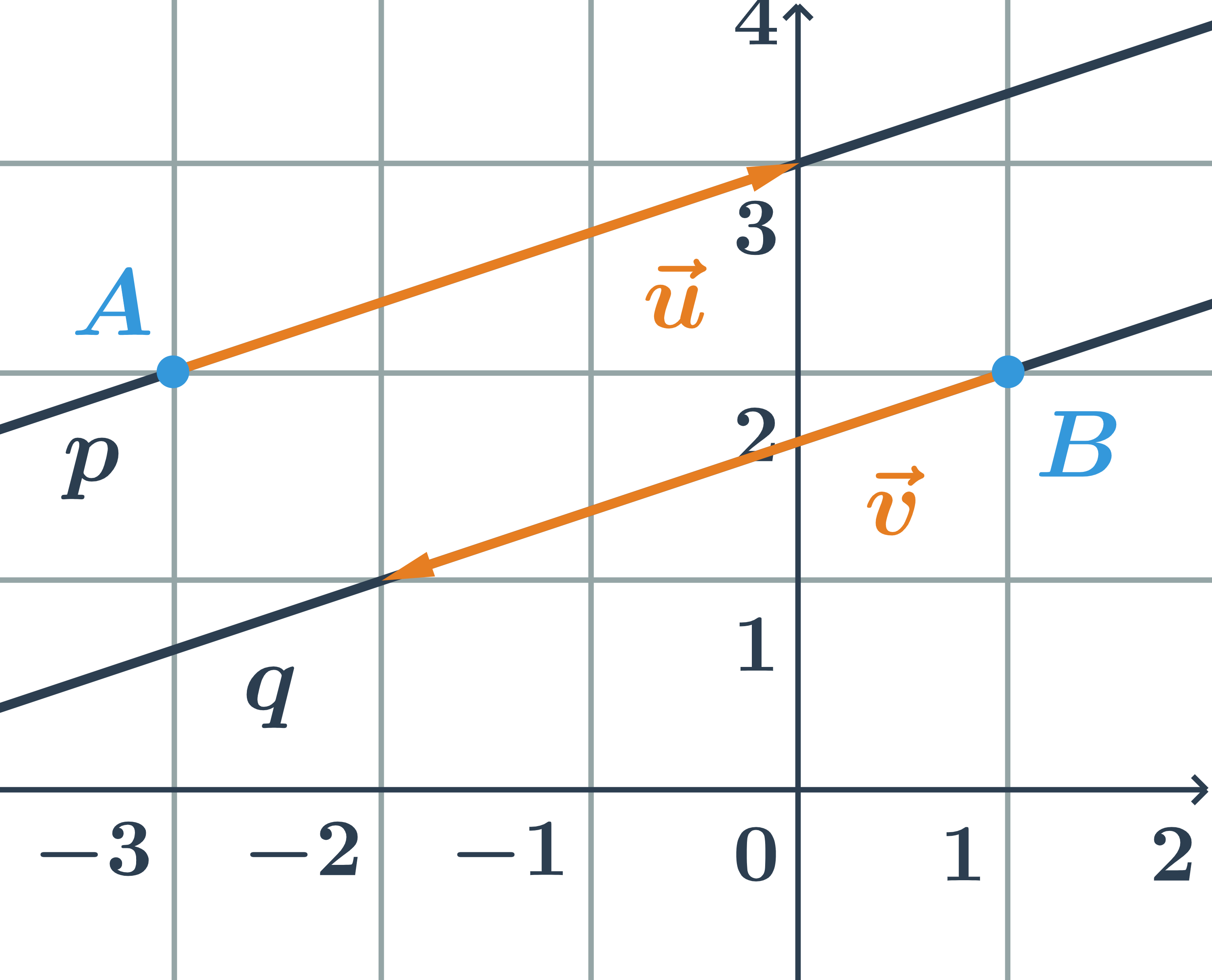
Rovnobežky zadané všeobecnými rovnicami
Určite vzájomnú polohu dvoch priamok daných všeobecnými rovnicami p: 2x+y-1=0 a q:4x+2y+3=0.
- normálový vektor priamky p:\hspace{0.25cm}\vec{n}=(2;1)
- normálový vektor priamky q:\hspace{0.25cm}\vec{m}=(4;2)
- Priamky p a q sú rovnobežné, pretože ich normálové vektory sú kolineárne.
- Overíme, že priamky nie sú totožné. Stačí určiť, či bod, ktorý leží na jednej priamke neleží na priamke druhej.
- Na priamke p leží napríklad bod A=[0;1].
- Overíme, či A leží na p dosadením súradníc bodu A do rovnice priamky p: 4\cdot0+2\cdot1+3\neq 0
- A nespĺňa rovnicu, takže neleží na priamke q \Rightarrow priamky nie sú totožné
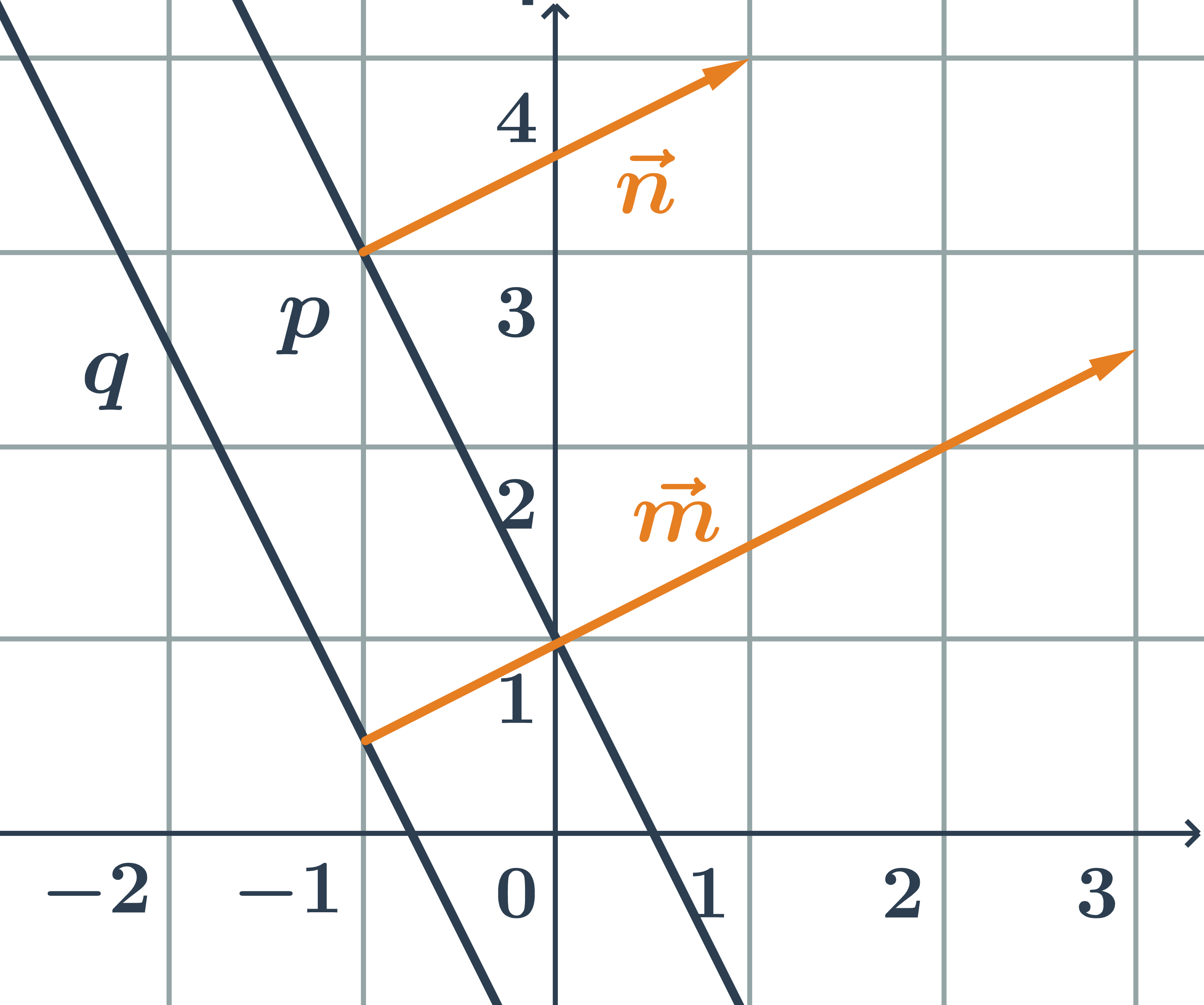
Rôznobežky zadané parametrickými rovnicami
Určite vzájomnú polohu priamok p, q zadaných parametricky:
p: \begin{array}{rrl}x&=&-1+t\\y&=&\hspace{0.25cm}3+2t\\&&\hspace{0.25cm}t\in\mathbb{R}\end{array} \hspace{0.5cm}q: \begin{array}{rrl}x&=&-4+s\\y&=&\hspace{0.25cm}3-s\\&&\hspace{0.25cm}s\in\mathbb{R}\end{array}
smerový vektor priamky p:\hspace{0.25cm}\vec{u}=(1;2)
smerový vektor priamky q:\hspace{0.25cm}\vec{v}=(1;-1)
Priamky p a q sú rôznobežné, pretože ich smerové vektory nie sú kolineárne.
Priesečník priamok spĺňa rovnice oboch priamok, teda každú z jeho súradníc je možné vyjadriť dvomi spôsobmi, dostávame nasledujúcu sústavu rovníc: \begin{array}{lrr}-1+t&=&-4+s\\\hspace{0.25cm}3+2t&=&3-s\end{array}
Sústavu môžeme vyriešiť sčítaním oboch rovníc: 2+3t=-1\Rightarrow3+3t=0\Rightarrow t=-1
Výsledný parameter t dosadíme do parametrických rovníc ktorejkoľvek z priamok a dostaneme súradnice x,y priesečníka.
Priesečník priamok p a q je bod R=[-2;1].
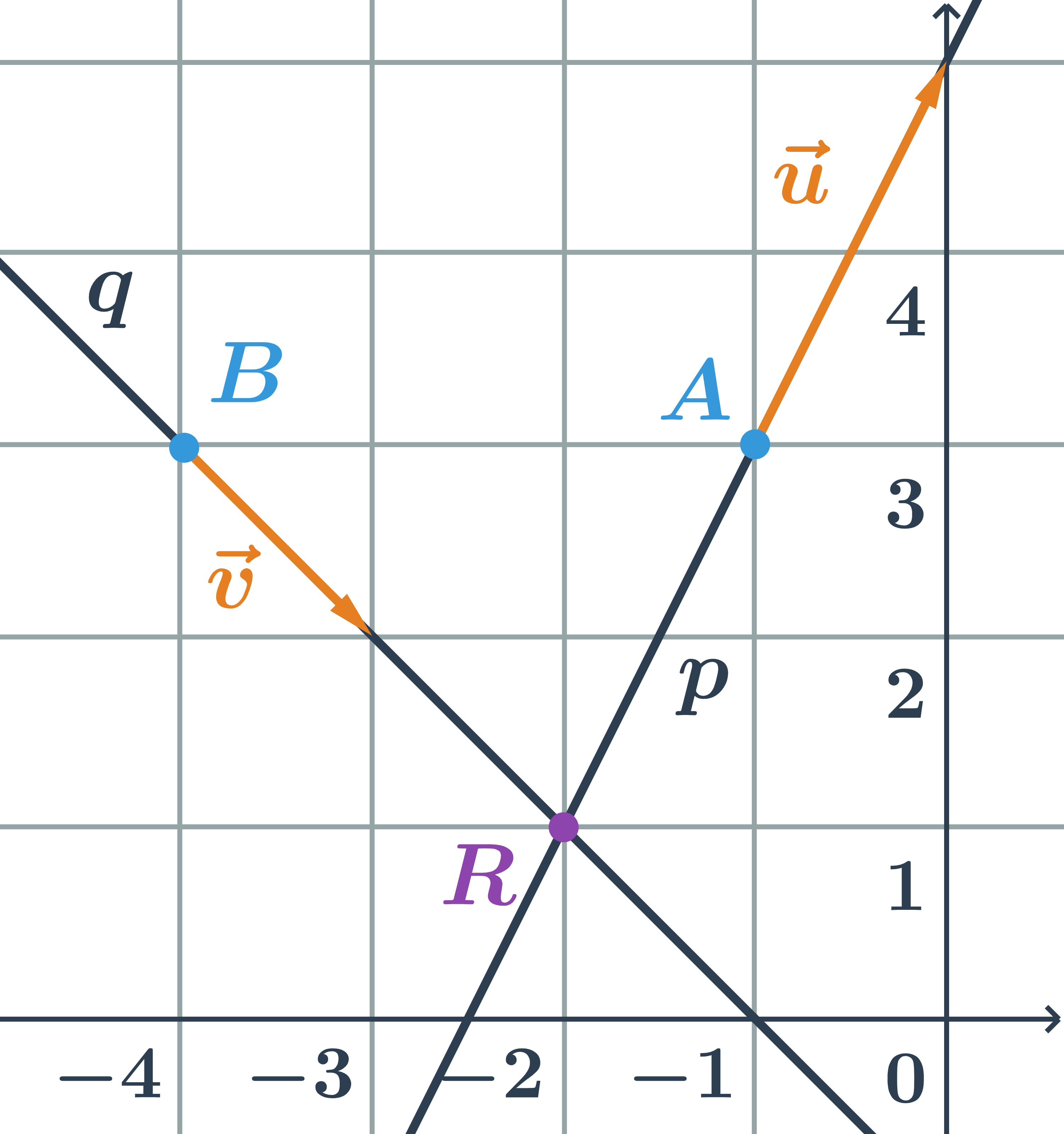
Rôznobežky zadané všeobecnými rovnicami
Určíme vzájomnú polohu dvoch priamok zadaných všeobecnými rovnicami p: 2x+y-1=0 a q:x-y+1=0.
- normálový vektor priamky p:\hspace{0.25cm}\vec{n}=(2;1)
- normálový vektor priamky q:\hspace{0.25cm}\vec{m}=(1;-1)
- Priamky p a q sú rôznobežné, pretože ich normálové vektory nie sú kolineárne.
- Priesečník priamok spĺňa rovnice oboch priamok, teda jeho súradnice sú riešením sústavy: \begin{array}{rrr}2x+y-1&=&0\\x-y+1&=&0\end{array}
- Môžeme vyriešiť sčítaním oboch rovníc: 3x=0\Rightarrow x=0
- Priesečník priamok p a q je bod R=[0;1]
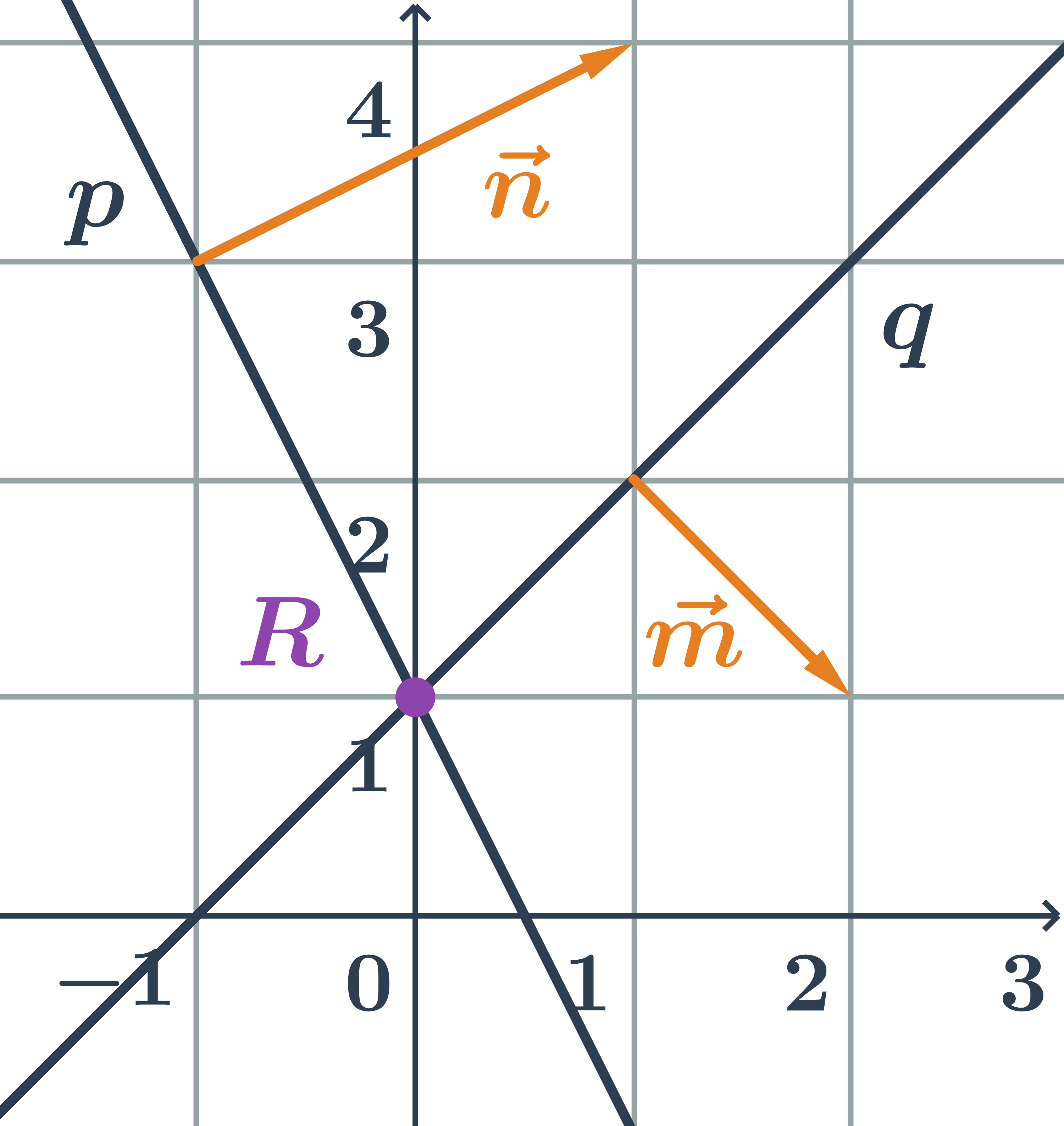
Priamka daná všeobecnou rovnicou a druhá parametricky – prvý príklad
Určite vzájomnú polohu priamok p,q zadaných takto:
\hspace{0.25cm}p: 2x-y+3=0\hspace{0.25cm} \hspace{0.5cm}q: \begin{array}{rrl}x&=&3-2t\\y&=&2-4t\\&&t\in\mathbb{R}\end{array}
- normálový vektor priamky p:\hspace{0.25cm}\vec{n}=(2;-1)
- smerový vektor priamky q:\hspace{0.25cm}\vec{v}=(-2;-4)
- Priamky p a q sú rovnobežné, pretože ich smerové vektory sú kolineárne. Preto je normálový vektor jednej priamky kolmý na smerový vektor druhej priamky.
- Overíme, že priamky nie sú totožné: stačí určiť, či bod, ktorý leží na jednej priamke neleží na priamke druhej.
- Na priamke q leží napríklad bod B=[3;2].
- Na priamke p tento bod neleží, čo zistíme dosadením súradníc bodu B do rovnice priamky: 2\cdot3-2+3\neq 0
- Bod B nespĺňa rovnicu, takže neleží na priamke p \Rightarrow priamky nie sú totožné
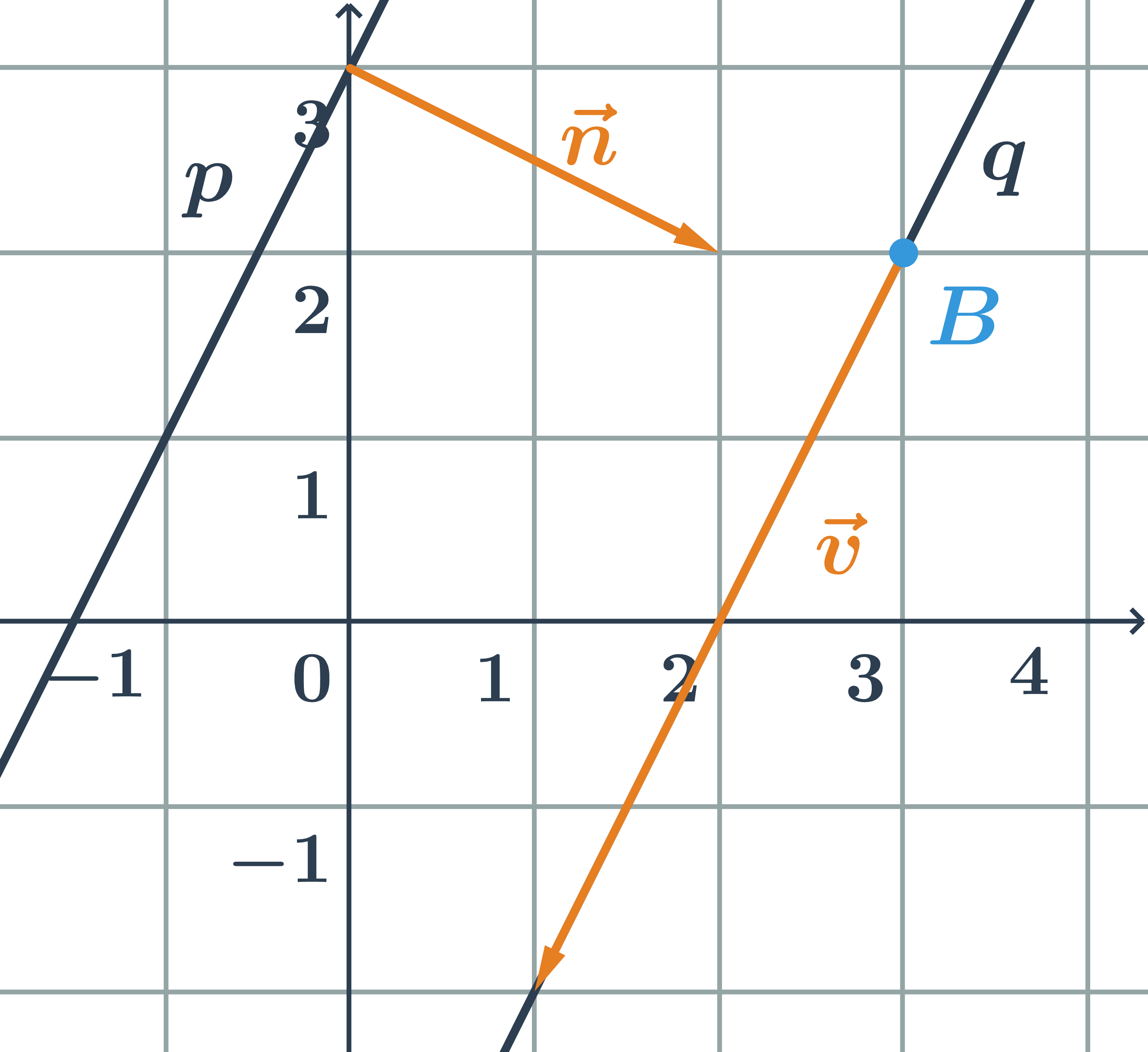
Priamka daná všeobecnou rovnicou a druhá parametricky – druhý príklad
Určite vzájomnú polohu priamok p,q zadaných:
\hspace{0.25cm}p: x-3y+3=0\hspace{0.25cm} \hspace{0.5cm}q: \begin{array}{rrl}x&=&\hspace{0.28cm}1+t\\y&=&-2+2t\\&&\hspace{0.28cm}t\in\mathbb{R}\end{array}
- normálový vektor priamky p:\hspace{0.25cm}\vec{n}=(1;-3)
- smerový vektor priamky q:\hspace{0.25cm}\vec{v}=(1;2)
- Priamky p a q sú rôznobežné, pretože ich smerové vektory nie sú kolineárne. Vyplýva z toho, že normálový vektor jednej priamky nie je kolmý na smerový vektoru druhej priamky.
- Priesečník priamok spĺňa rovnice oboch priamok, teda jeho súradnice nájdeme tak, že parametrické vyjadrenie priamky q dosadíme do všeobecnej rovnice priamky p: \begin{array}{rrl}(1+t)-3(-2+2t)+3&=&0\\1+t+6-6t+3&=&0\\10-5t&=&0\\t&=&2\end{array}
- Priesečník priamok p a q je bod R=[3;2]
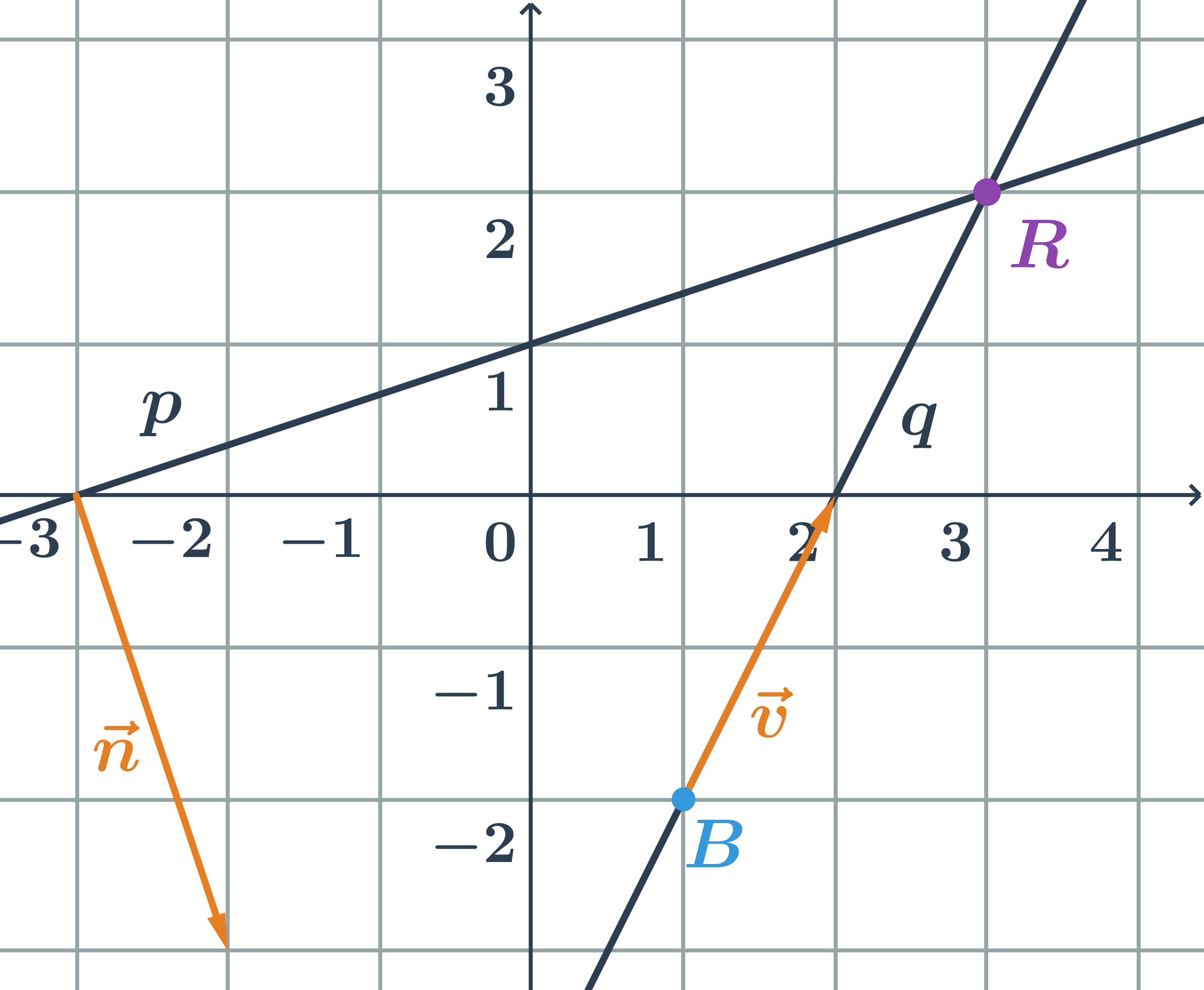
Súvislosť počtu spoločných bodov priamok s počtom riešení sústavy rovníc
Na určenie spoločného bodu (bodov) dvoch priamok, vždy riešime sústavu rovníc. Táto sústava môže mať:
- jedno riešenie – priamky sú rôznobežné
- žiadne riešenie – priamky sú rovnobežné
- nekonečne veľa riešení – priamky sú totožné
Počet spoločných bodov – prvý príklad
Hľadáme priesečník(y) priamok p,q zadaných ako: \hspace{0.25cm}p: x-3y+3=0\hspace{0.25cm} a \hspace{0.25cm}q: \begin{array}{rrl}x&=&\hspace{0.28cm}1+t\\y&=&-2+2t\end{array}
- Dosadíme parametrické vyjadrenie do všeobecnej rovnice a riešime sústavu rovníc:
\begin{array}{rrl}(1+t)-3(-2+2t)+3&=&0\\1+t+6-6t+3&=&0\\10-5t&=&0\\t&=&2\end{array}
- Jedno riešenie \Rightarrow rôznobežné priamky
Počet spoločných bodov – druhý príklad
Hľadáme priesečník(y) priamok p,q zadaných ako: \hspace{0.25cm}p: 2x-y+3=0\hspace{0.25cm} a \hspace{0.25cm}q: \begin{array}{rrl}x&=&3-2t\\y&=&2-4t\end{array}
- Dosadíme parametrické vyjadrenie do všeobecnej rovnice a riešime sústavu rovníc:
\begin{array}{rrl}2(3-2t)-(2-4t)+3&=&0\\6-4t-2+4t+3&=&0\\7&=&0\end{array}
- Žiadne riešenie \Rightarrow rôzne rovnobežné priamky
Počet spoločných bodov – tretí príklad
Hľadáme priesečník(y) priamok p,q zadaných ako: \hspace{0.25cm}p: 2x-y+3=0\hspace{0.25cm} a \hspace{0.25cm}q: \begin{array}{rrl}x&=&3+t\\y&=&9+2t\end{array}
- Dosadíme parametrické vyjadrenie do všeobecnej rovnice a riešime sústavu rovníc:
\begin{array}{rrl}2(3+t)-(9+2t)+3&=&0\\6+2t-9-2t+3&=&0\\0&=&0\end{array}
- Nekonečne veľa riešení \Rightarrow totožné priamky
Vzájomná poloha priamky a bodu v rovine
Bod leží na priamke, ak jeho súradnice vyhovujú rovnici priamky.
- Ak je priamka daná všeobecnou rovnicou, po dosadení súradníc bodu, ktorý na priamke leží do rovnice priamky nastane rovnosť.
- Ak je priamka daná parametricky, po dosadení súradníc bodu vychádza z oboch rovníc rovnaká hodnota parametra t.
Bod a priamka daná všeobecnou rovnicou
Určite, či body A=[2;3] a B=[-1;2] ležia na priamke p:2x-3y+5=0.
- Do rovnice priamky dosadíme súradnice bodu A=[2;3]:
- 2\cdot 2-3\cdot3+5=0\Rightarrow bod A leží na priamke p
- Do rovnice priamky dosadíme súradnice bodu B=[-1;2]:
- 2\cdot (-1)-3\cdot2+5=-3\Rightarrow bod B neleží na priamke p
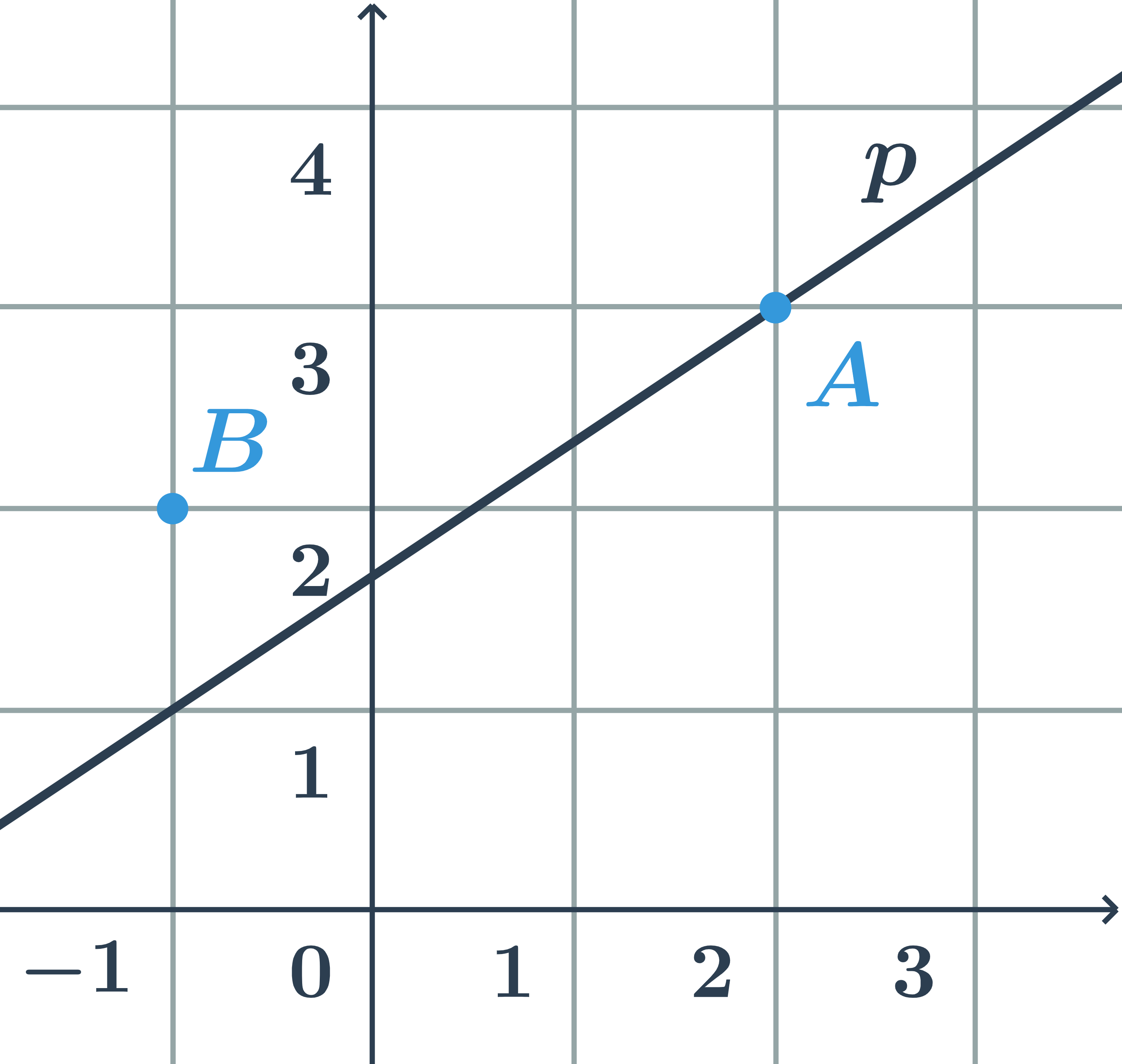
Bod a priamka daná parametricky
Určite, či body A=[3;1] a B=[4;4] ležia na priamke p danej parametricky: \begin{array}{rrl}x&=&2-t\\y&=&3+2t\\&&t\in\mathbb{R}\end{array}
- Do rovníc priamky dosadíme súradnice bodu A=[3;1]:
\begin{array}{rrrr}3&=&2-t&\Rightarrow t=-1\\1&=&3+2t&\Rightarrow t=-1\end{array} \Rightarrow bod A leží na priamke p
- Do rovnice priamky dosadíme súradnice bodu B=[4;5]:
\begin{array}{rrrl}4&=&2-t&\Rightarrow t=-2\\5&=&3+2t&\Rightarrow t=1\end{array}\Rightarrow bod B neleží na priamke p
Polohové úlohy
V polohových úlohách riešime analyticky vzájomnú polohu geometrických útvarov v rovine. Najčastejšie ide o vzájomnú polohu dvoch priamok alebo o vzájomnú polohu priamky a bodu.
HoreMetrické úlohy
V metrických úlohách v analytickej geometrii býva úlohou vypočítať konkrétnu číselnú hodnotu veličín ako je:
- vzdialenosť dvoch objektov, napr. vzdialenosť bodu od priamky,
- odchýlka dvoch priamok v rovine.
Vzdialenosť bodu od priamky
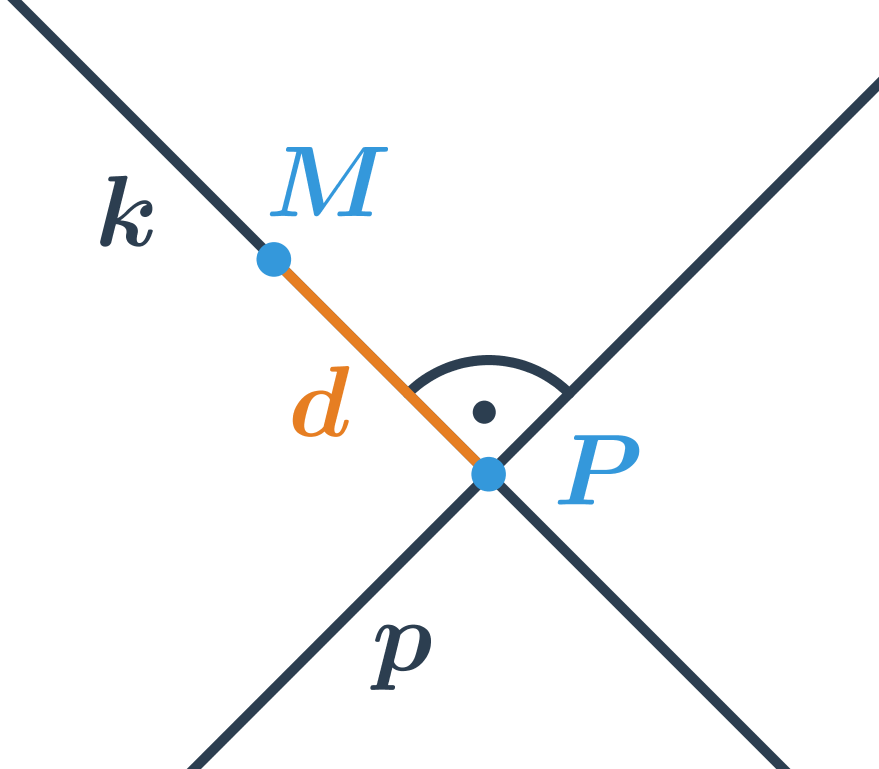
Vzdialenosť bodu od priamky je dĺžka najkratšej úsečky určenej bodom M a bodom ležiacim na priamke p. Ako je vidieť z obrázka, táto najkratšia úsečka leží na kolmici z bodu M k priamke p. Vzdialenosť bodu od priamky teda môžeme určiť takto:
- nájdeme priamku k, ktorá prechádza bodom M a je kolmá na priamku p
- určíme priesečník P priamky k s priamkou p
- vzdialenosť bodu M od priamky p je dĺžka úsečky PM
Príklad: vzdialenosť bodu od priamky – pomocou kolmice
Určite vzdialenosť bodu M=[5;2] od priamky p:4x+3y-1=0.
- Priamka k, ktorá prechádza bodom M a je kolmá na priamku p má smerový vektor kolineárny s normálovým vektorom priamky p.
- Súradnice smerového vektora priamky k sú: \vec{u}=(4;3).
- Priamka k má parametrické vyjadrenie: p:X=M+t\vec{u}
- p:\begin{array}{rrl}x&=&5+4t\\y&=&2+3t\\&&t\in\mathbb{R}\end{array}
- Súradnice priesečníka P priamky k s priamkou p určíme dosadením parametrického vyjadrenia priamky k do všeobecnej rovnice priamky p.
\begin{array}{rrl}4(5+4t)+3(2+3t)-1&=&0\\20+16t+6+9t-1&=&0\\25+25t&=&0\Rightarrow t=-1\end{array}
- Priesečník priamok k a p je bod P=[1;-1].
- Vzdialenosť bodu M od priamky p je dĺžka úsečky PM:
- Vzorec pre dĺžku úsečky: d=\sqrt{(x_M-x_P)^2+(y_M-y_P)^2}
- Dosadíme súradnice bodov M,P: d=\sqrt{(5-1)^2+(2-(-1))^2}=\sqrt{16+9}=5
Vzorec pre vzdialenosť bodu od priamky danej všeobecnou rovnicou
Vzdialenosť bodu M=[m_1;m_2] od priamky p danej všeobecnou rovnicou ax+by+c=0 je daná vzorcom: d=\frac{\left| am_1+bm_2+c \right|}{\sqrt{a^2+b^2}}
Príklad: vzdialenosť bodu od priamky – pomocou vzorca
Určite vzdialenosť bodu M=[5;2] od priamky p:4x+3y-1=0 s využitím vzorca.
- Dosadíme do vzorca d=\frac{\left| am_1+bm_2+c \right|}{\sqrt{a^2+b^2}} súradnice bodu M=[5;2] a koeficienty a a b zo všeobecnej rovnice priamky.
- Všeobecná rovnica pre p je 4x+3y-1=0, teda a=4 a b=3.
- Máme: d=\frac{\left| 4\cdot5+3\cdot2-1\right|}{\sqrt{4^2+3^2}}=\frac{25}{\sqrt{25}}=5
Vzdialenosť dvoch rovnobežiek
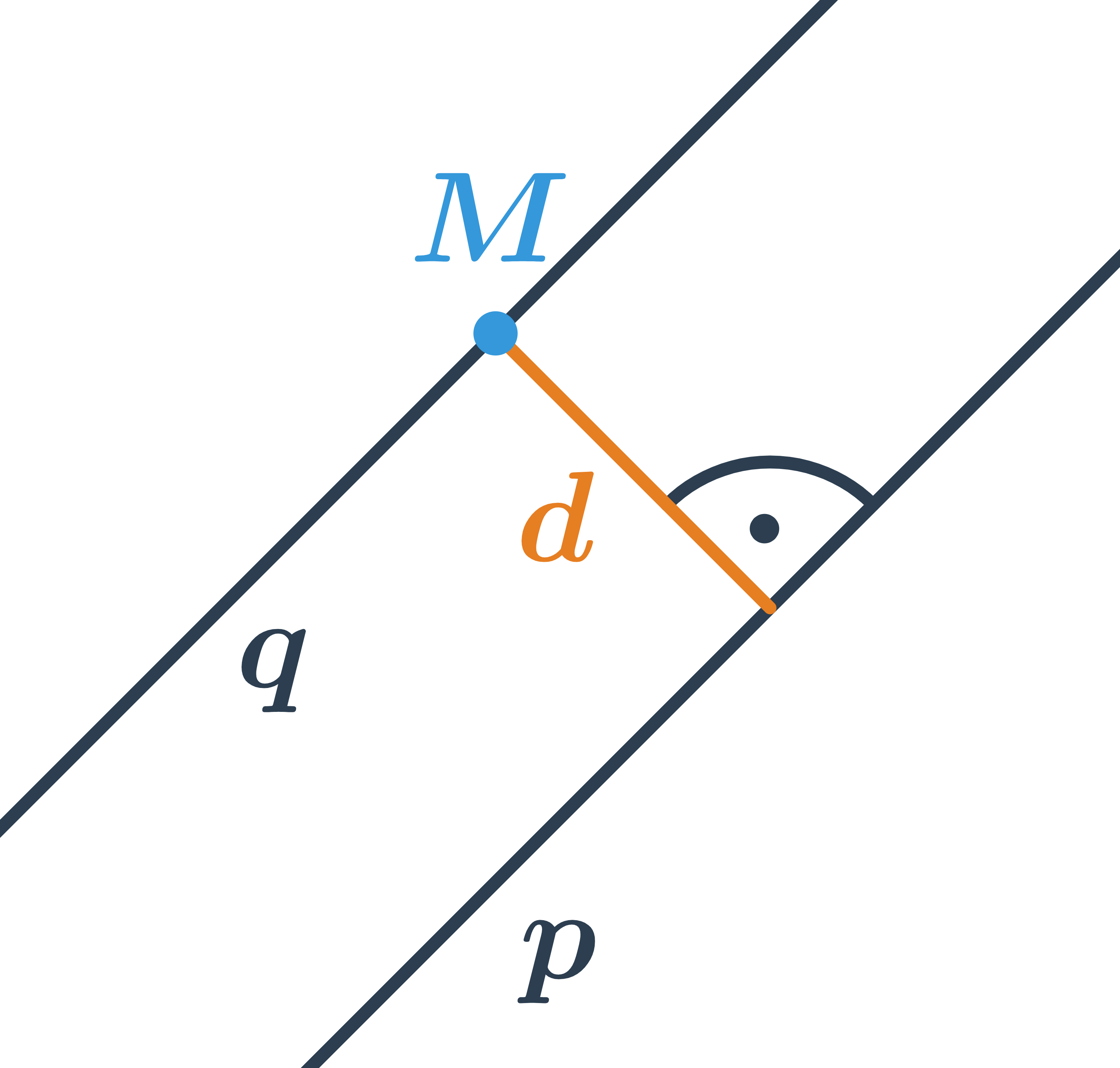
Ak vieme určiť vzdialenosť bodu od priamky, ľahko určíme tiež vzdialenosť dvoch rovnobežiek. Stačí si uvedomiť, že všetky body ležiace na jednej priamke majú od druhej priamky rovnakú vzdialenosť. Preto je vzdialenosť rovnobežiek rovnaká ako vzdialenosť ľubovoľného bodu na jednej priamke od priamky druhej.
Príklad: vzdialenosť rovnobežiek
Určite vzdialenosť rovnobežiek p:2x-4y+3=0 a q:x-2y+1=0.
- Určíme súradnice jedného bodu (M) na priamke q tak, že jednu súradnicu zvolíme a druhú dopočítame.
- Zvolíme napríklad súradnicu y=0, potom x-2\cdot0+1=0\Rightarrow x=-1
- Dosadíme do vzorca d=\frac{\left| am_1+bm_2+c \right|}{\sqrt{a^2+b^2}} súradnice bodu M=[-1;0] a koeficienty a a b zo všeobecnej rovnice priamky p.
- Všeobecná rovnica pre p je 2x-4y+3=0, teda a=2 a b=-4.
- Máme: d=\frac{\left| 2\cdot(-1)-4\cdot0+3\right|}{\sqrt{2^2+(-4)^2}}=\frac{1}{\sqrt{20}}
- Vzdialenosť rovnobežiek p a q je: d=\frac{1}{\sqrt{20}}
Odchýlka dvoch priamok
Odchýlka rovnobežiek je 0^\circ. Odchýlka rôznobežiek je veľkosť ostrého alebo pravého uhla, ktorý priamky zvierajú.
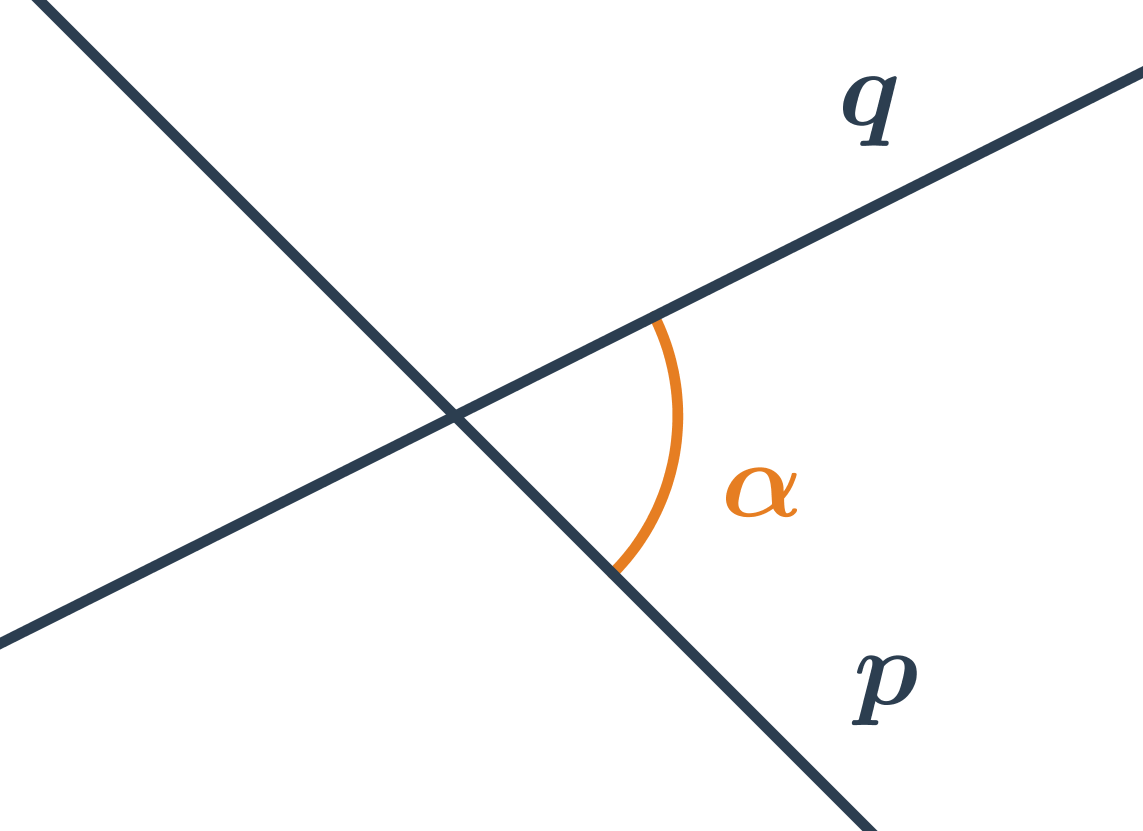
Odchýlku rôznobežiek p a q môžeme vypočítať na základe znalosti smerových alebo normálových vektorov priamok. Vzorec na výpočet uhlov rôznobežiek je podobný ako vzorec na výpočet uhla vektorov.
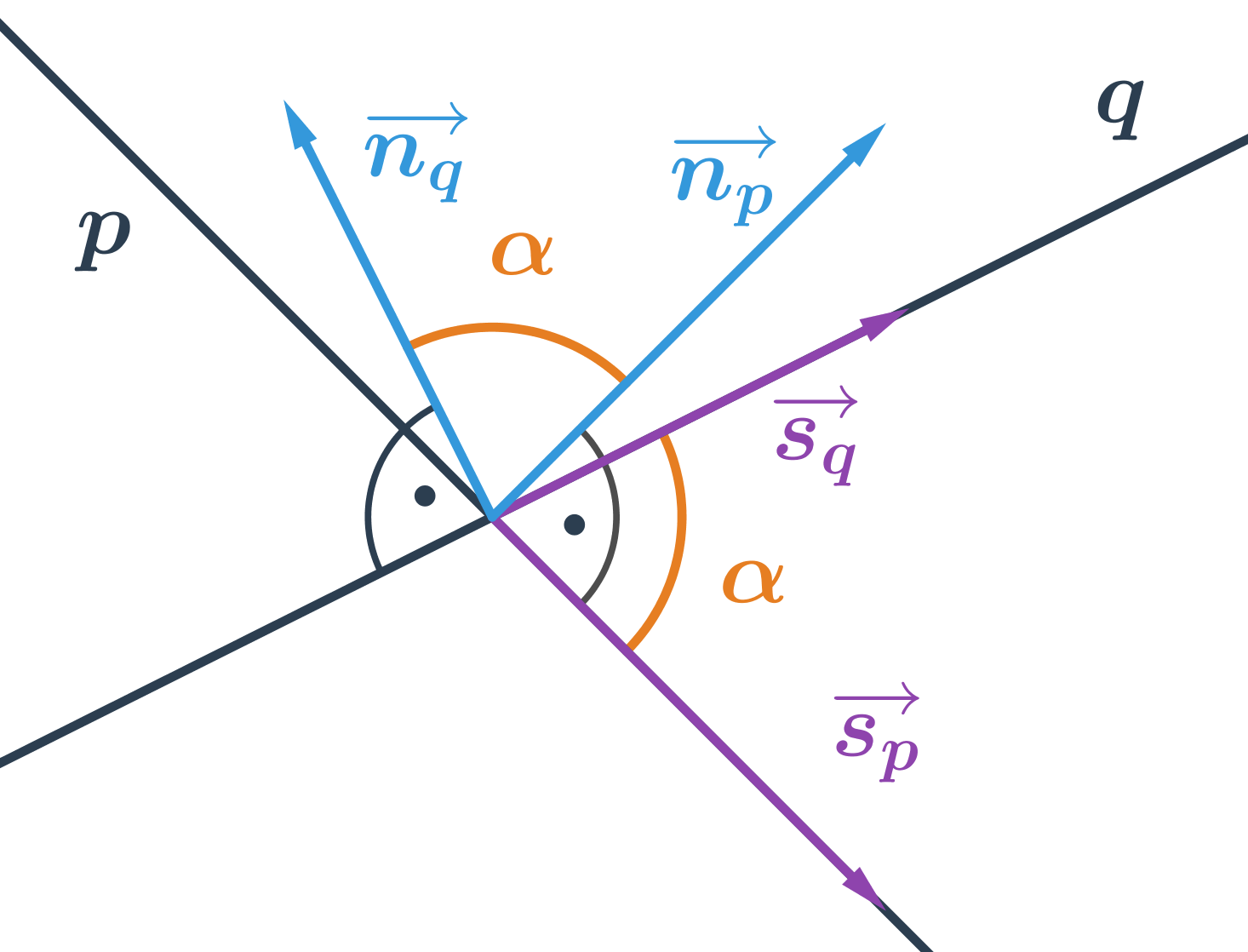
Odchýlka rôznobežiek je uhol \alpha, pre ktorý platí: \cos \alpha =\frac{\left| \vec{u} \cdot \vec{v} \right|}{\left| \vec{u} \right|\cdot \left| \vec{v} \right|} Vektory \vec{u} a \vec{v} uvedené vo vzorci sú smerové vektory \overrightarrow{s_p} a \overrightarrow{s_q} alebo normálové vektory \overrightarrow{n_p} a \overrightarrow{n_q} priamok p a q.
Pre dve na seba kolmé priamky platí, že ich odchýlka \alpha=90^\circ a teda \cos\alpha=0.
Prečo musí byť vo vzorci pre výpočet odchýlky priamok absolútna hodnota?
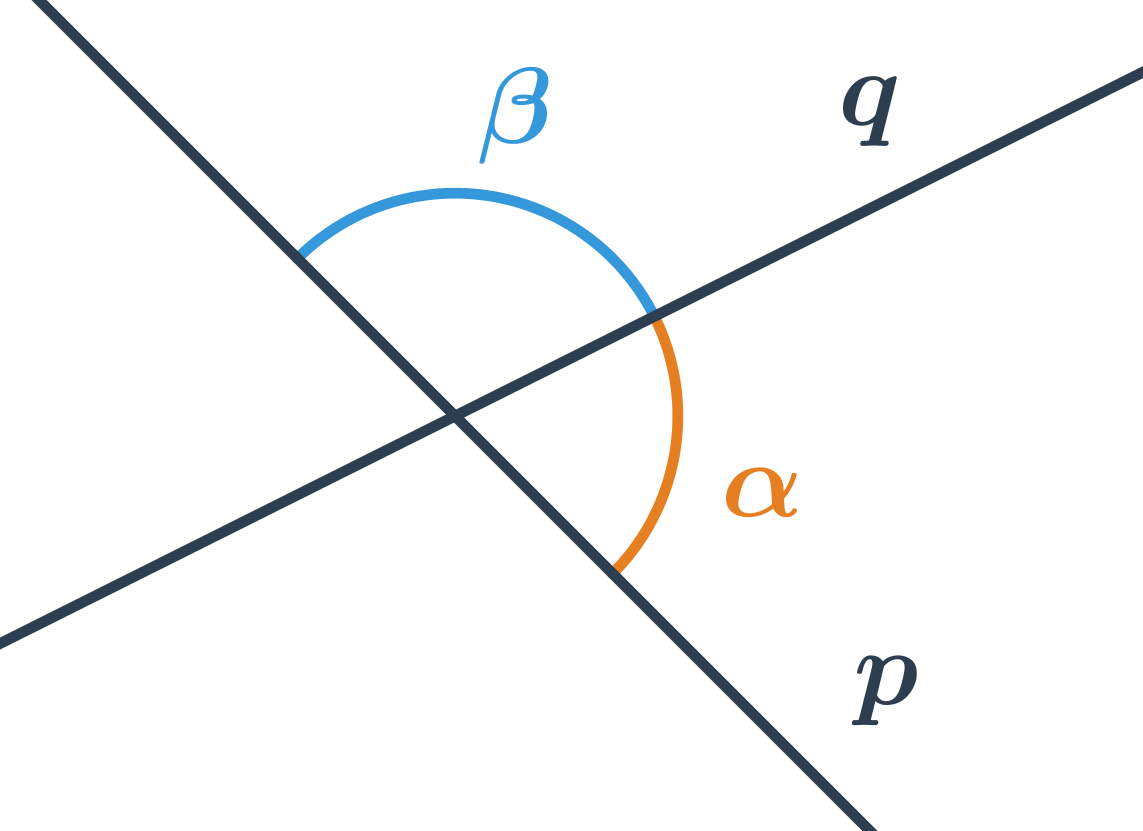
- Odchýlka priamok p a q na obrázku je ostrý uhol \alpha, nie tupý uhol \beta.
- \alpha a \beta sú vedľajšie uhly, pre ktoré je hodnota funkcie \cos opačná, teda: \cos\alpha=-\cos\beta
- Pre uhol \alpha je \cos\alpha > 0, pre \beta je \cos\beta < 0
- Absolútna hodnota vo vzorci nám zaručí, že nájdeme uhol, kde hodnota funkcie \cos je kladná, teda uhol ostrý, ktorý je odchýlkou daných priamok.
Odchýlka priamok a uhly v trojuholníku
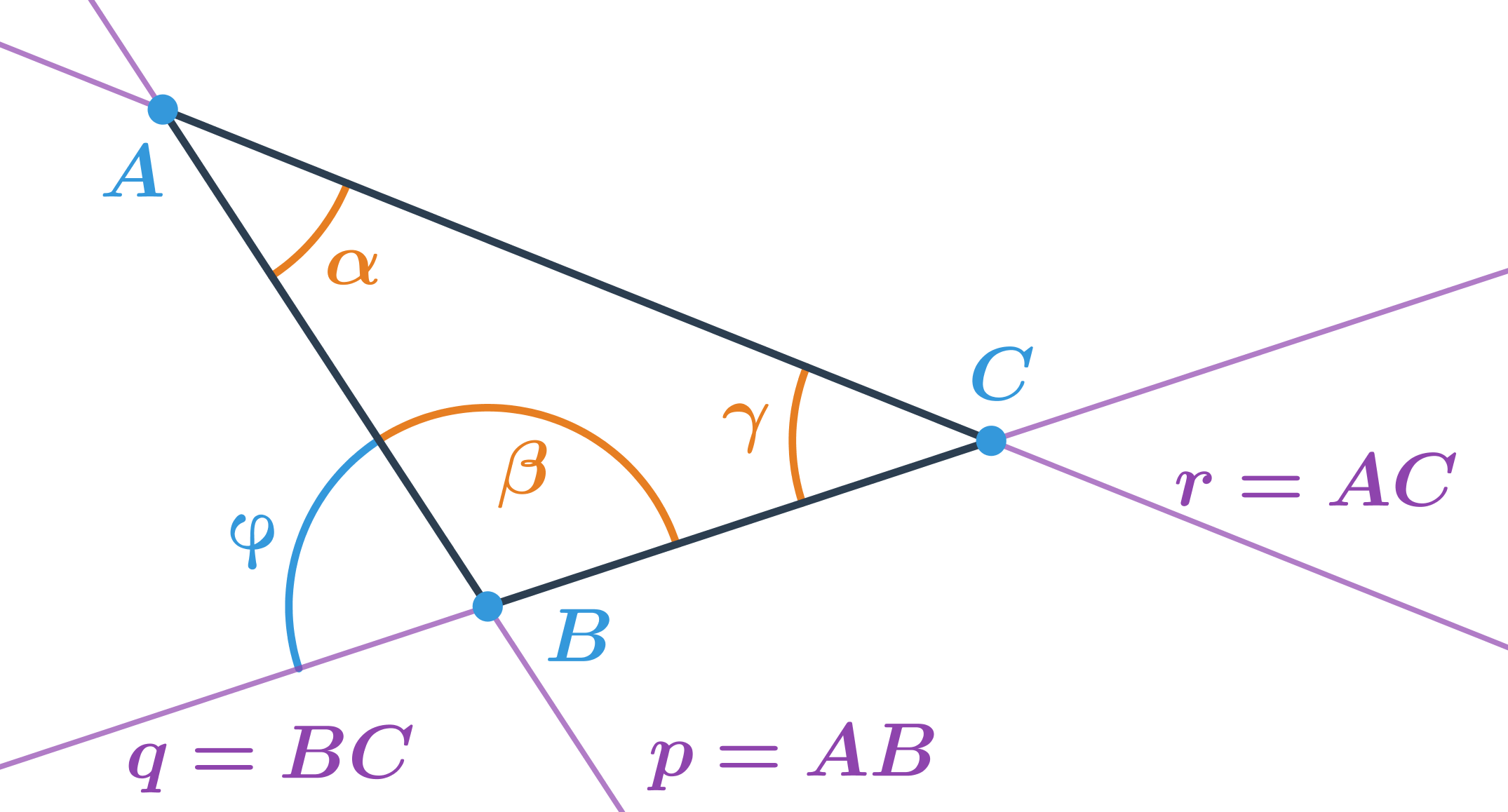
V trojuholníku na obrázku:
- uhol \alpha je menší než 90^\circ a je to odchýlka priamok AB a AC
- uhol \beta je väčší než 90^\circ a nie je to odchýlka priamok AB a BC
- uhol \gamma je menší než 90^\circ a je to odchýlka priamok BC a AC
Veľkosť uhlov v trojuholníku nemusí byť rovnaká ako odchýlka priamok, na ktorých ležia strany trojuholníka. Uhly v trojuholníku počítame ako odchýlku vektorov, ktoré určujú daný uhol. Tento uhol môže byť väčší než 90^\circ, preto využijeme vzorec pre výpočet odchýlky vektorov (vo vzorci nebude absolútna hodnota).
Odchýlka priamok
Určite odchýlku priamok p:x-2y+3=0 a q:2x-y+1=0
- Priamky sú dané všeobecnými rovnicami, preto pre výpočet ich odchýlky využijeme normálové vektory: \overrightarrow{n_p}=(1;-2) a \overrightarrow{n_q}=(2;-1)
- Dosadíme do vzorca: \cos \alpha =\frac{\left| \vec{u} \cdot \vec{v} \right|}{\left| \vec{u} \right|\cdot \left| \vec{v} \right|}=\frac{\left| 1\cdot2+(-2) \cdot(-1) \right|}{\sqrt{1^2+(-2)^2}\cdot\sqrt{2^2+(-1)^2}}=\frac{4}{\sqrt{5}\cdot \sqrt{5}}=\frac{4}{5}
- Pomocou funkcie cos^{-1} na kalkulačke dopočítame odchýlku: \alpha=36^\circ
Rovina je určená tromi bodmi, ktoré neležia na jednej priamke. Z predchádzajúcich kapitol už vieme, že dvojica bodov určuje priamku, prípadne vektor, preto je veľa ďalších spôsobov, ako určiť rovinu:
- bodom a priamkou
- dvomi rôznobežnými priamkami
- dvomi rovnobežnými priamkami
- bodom a dvomi vektormi
V priestore je možné zapísať rovinu ako množinu bodov, ktoré spĺňajú parametrickú rovnicu alebo všeobecnú rovnicu.
Ak máme rovinu popísanú rovnicou, dokážeme určiť vzájomnú polohu roviny a bodu výpočtom.
HoreRoviny: pojmy
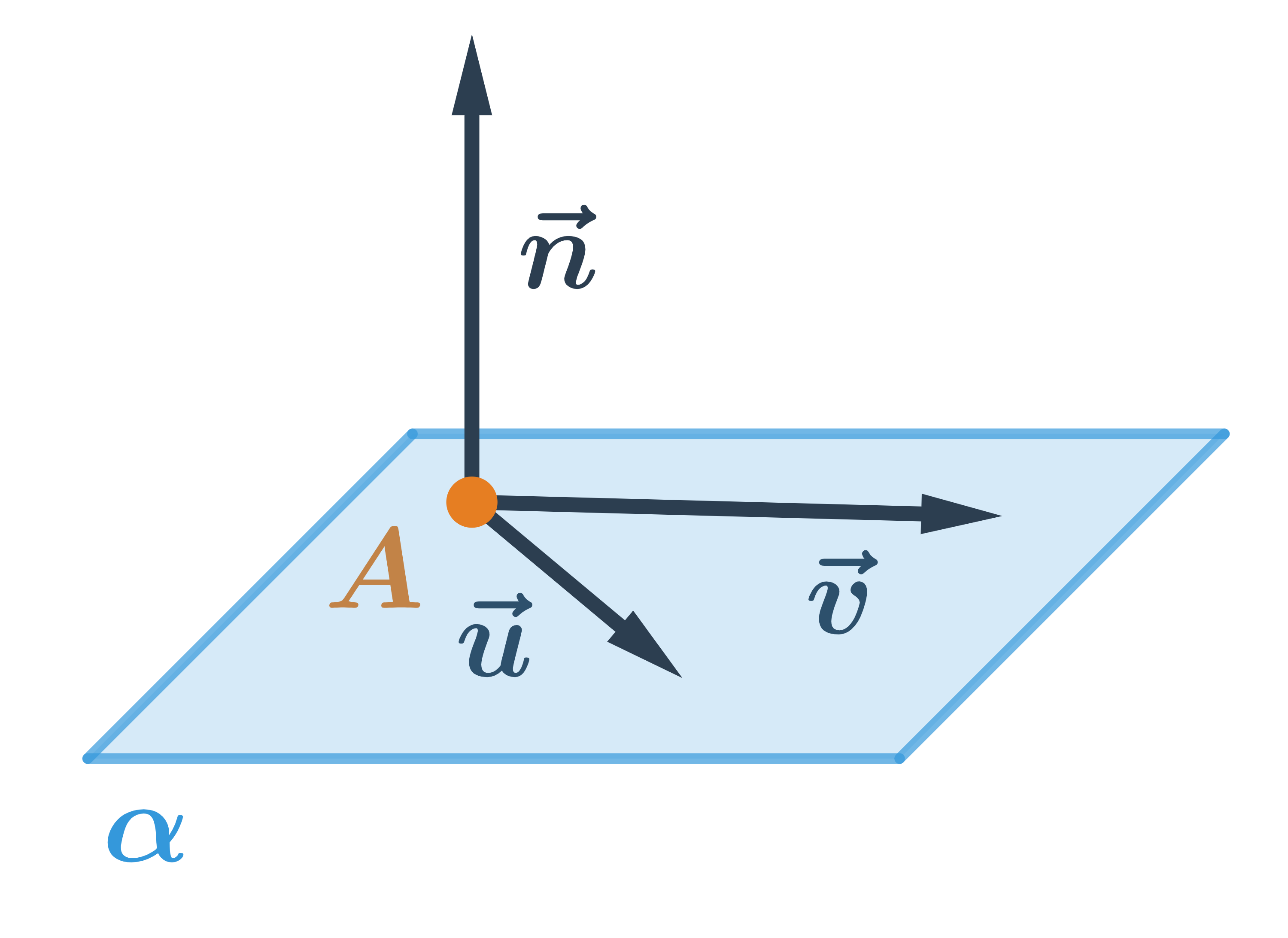
Priamka je jednoznačne určená bodom a dvomi vektormi, ktoré nie sú kolineárne. Na obrázku je rovina \alpha určená bodom A a vektormi \vec{u}, \vec{v}. Každý vektor, ktorý je kolmý na rovinu \alpha sa nazýva normálový vektor roviny \alpha. Na obrázku je normálový vektor \vec{n}.
Parametrické rovnice roviny
Rovina určená bodom A=[a_1;a_2;a_3] a vektormi \vec{u}=(u_1;u_2;u_3) a \vec{v}=(v_1;v_2;v_3) má parametrické rovnice tvaru:
\begin{array}{rrl}x&=&a_1+t\cdot u_1+s\cdot v_1\\y&=&a_2+t\cdot u_2+s\cdot v_2\\z&=&a_3+t\cdot u_3+s\cdot v_3\\&&t,s\in\mathbb{R}\end{array}
Skrátene môžeme vyjadriť \alpha:X=A+t\vec{u}+s\vec{v}, kde t, s nazývame parametrami.
Všeobecná rovnica roviny
Všeobecná rovnica roviny je v tvare ax+by+cz+d=0, kde konštanty a, b, c sú súradnice normálového vektora a d reálne číslo.
Všeobecná rovnica roviny rovnobežnej s osami x a y
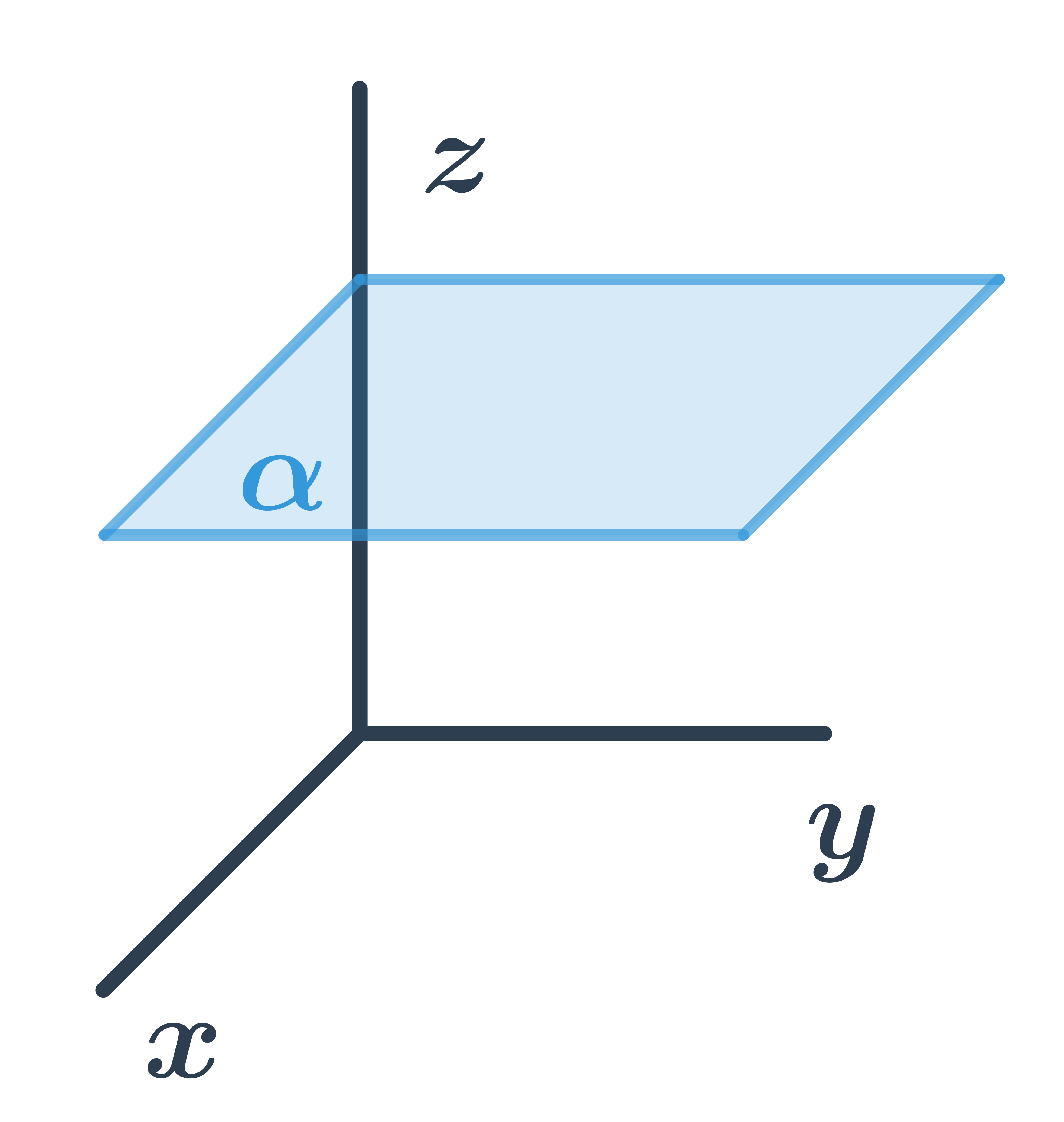
Pre všetky body ležiace v rovine je tretia súradnica rovnaká, teda rovina má všeobecnú rovnicu: z+d=0.
Všeobecná rovnica roviny rovnobežnej s osami x a z
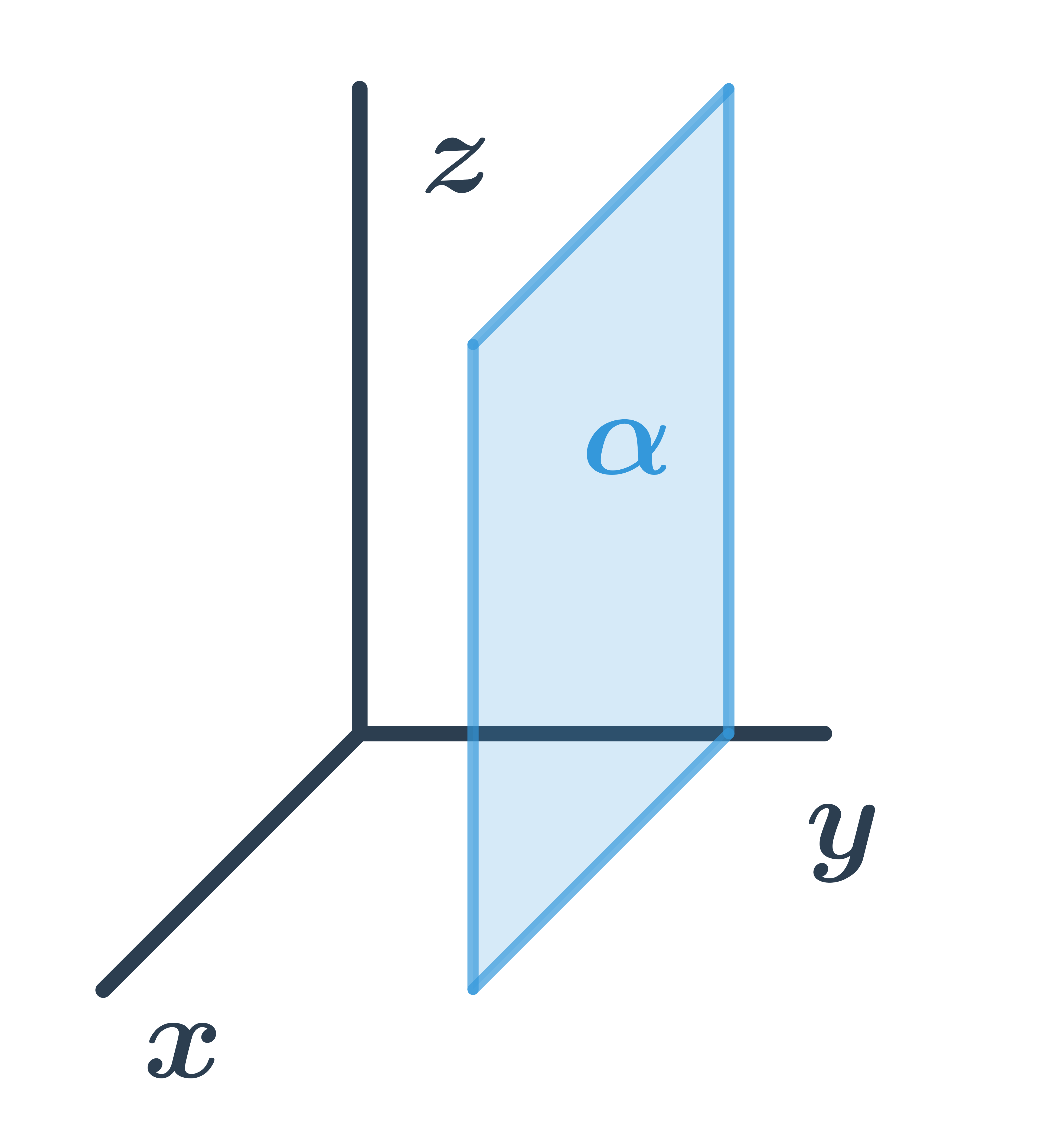
Pre všetky body ležiace v rovine je druhá súradnica rovnaká, teda rovina má všeobecnú rovnicu: y+d=0.
Všeobecná rovnica roviny rovnobežnej s osami y a z
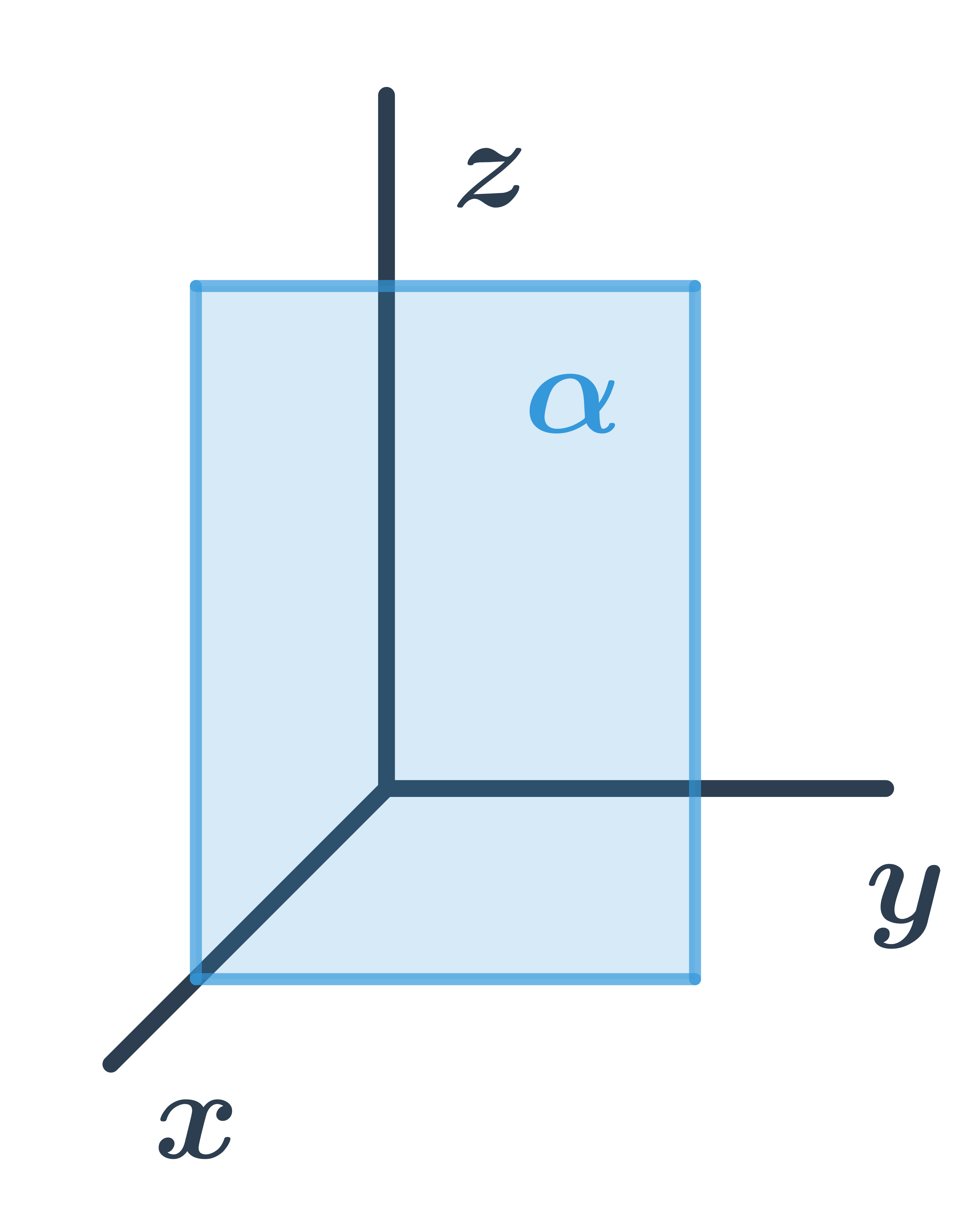
Pre všetky body ležiace v rovine je prvá súradnica rovnaká, teda rovina má všeobecnú rovnicu: z+d=0.
Bod a rovina
Bod M=[m_1;m_2;m_3] leží v rovine, ak jeho súradnice vyhovujú rovnici roviny.
- Ak je rovina daná všeobecnou rovnicou ax+by+cz+d=0, pre súradnice bodu, ktorý leží na priamke platí: a\cdot m_1+b\cdot m_2+c\cdot m_3+d=0
- Ak je rovina daná parametricky, po dosadení súradníc bodu do parametrických rovníc dostaneme sústavu troch rovníc pre dve neznáme t, s, ktorá má presne jedno riešenie (dvojicu reálnych čísel).
Všeobecná rovnica roviny, ktorá prechádza počiatkom
- Rovina prechádza bodom O=[0;0;0], musí teda platiť: a\cdot0+b\cdot0+c\cdot0+d=0\Rightarrow d=0.
- Rovina, ktorá prechádza počiatkom má všeobecnú rovnicu: ax+by+cz=0.
Dve rovnobežné roviny
Normálové vektory dvoch rovnobežných rovín \alpha: a_1x+b_1y+c_1z+d_1=0 a \beta: a_2x+b_2y+c_2z+d_2=0 sú kolineárne, teda súradnice jedného vektora sú k-násobok súradníc druhého vektora. Pre konštanty vo všeobecných rovniciach musí platiť:
\begin{array}{rll}a_2&=&k\cdot a_1\\ b_2&=&k\cdot b_1\\c_2&=&k\cdot c_1\\&&k\in\mathbb{R}\end{array}
Ak by platilo i d_2=k\cdot d_1 roviny sú totožné.
HoreParametrické rovnice roviny
Na určenie parametrických rovníc roviny potrebujeme poznať súradnice jedného bodu a dvoch nekolineárnych vektorov v rovine \alpha. Rovina určená bodom A=[a_1;a_2;a_3] a vektormi \vec{u}=(u_1;u_2;u_3) a \vec{v}=(v_1;v_2;v_3) má parametrické rovnice tvaru:
\begin{array}{rrl}x&=&a_1+t\cdot u_1+s\cdot v_1\\y&=&a_2+t\cdot u_2+s\cdot v_2\\z&=&a_3+t\cdot u_3+s\cdot v_3\\&&t,s\in\mathbb{R}\end{array}
Skrátene môžeme vyjadriť \alpha:X=A+t\vec{u}+s\vec{v}, kde t,s \in \mathbb{R} sú parametre.
Parametrické rovnice roviny určenej tromi bodmi
Určite parametrické rovnice roviny \alpha určenej body A=[3;2;1], B=[1;3;4], C=[2;-3;3].
- rovina \alpha je určená bodom A a vektormi \vec{u}=\overrightarrow{AB}, \vec{v}=\overrightarrow{AC}:
- \vec{u}=\overrightarrow{AB}=B-A=(-2;1;3)
- \vec{v}=\overrightarrow{AC}=C-A=(-1;-5;2)
- parametrické rovnice roviny \alpha sú:
\begin{array}{rrl}x&=&3-2t-s\\y&=&2+t-5s\\z&=&1+3t+2s\\&&t,s\in\mathbb{R}\end{array}
Parametrické rovnice roviny určenej bodom a dvomi vektormi
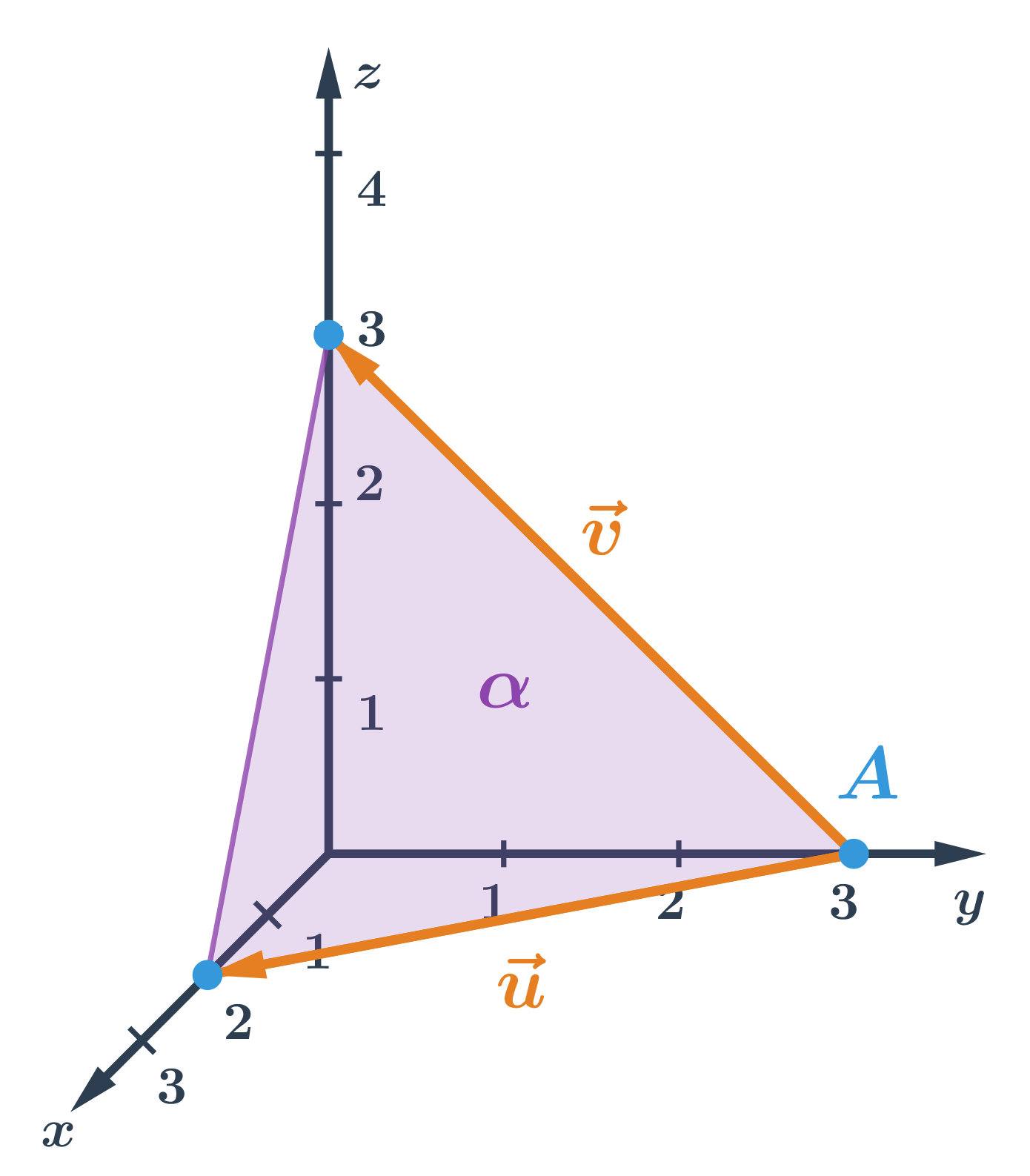
- rovina \alpha je určená bodom A a vektormi \vec{u}, \vec{v}
- súradnice určíme z obrázka:
- A=[0;3;0],
- \vec{u}=(2;-3;0),
- \vec{v}=(0;-3;3)
- parametrické rovnice roviny \alpha sú:
\begin{array}{rrl}x&=&2t\\y&=&3-3t-3s\\z&=&3s\\&&t,s\in\mathbb{R}\end{array}
Parametrické rovnice roviny určenej rôznobežkami p a q
Určite parametrické rovnice roviny určenej dvomi rôznobežkami s nasledujúcimi parametrickými rovnicami:
p:\begin{array}{rrl}x&=&2+3t\\y&=&1+2t\\z&=&4-4t\\&&t\in\mathbb{R}\end{array}, q:\begin{array}{rrl}x&=&2+4s\\y&=&1-2s\\z&=&4-5s\\&&s\in\mathbb{R}\end{array}
- rovina \alpha je určená spoločným bodom rôznobežiek a smerovými vektormi priamok p a q
- spoločný bod rôznobežiek: R=[2;1;4],
- smerový vektor priamky p:\vec{u}=(3;2;4),
- smerový vektor priamky q:\vec{v}=(4;-2;-5)
- parametrické rovnice roviny \alpha sú:
\begin{array}{rrl}x&=&2+3t+4s\\y&=&1+2t-2s\\z&=&4-4t-5s\\&&t,s\in\mathbb{R}\end{array}
Všeobecná rovnica roviny
Všeobecná rovnica roviny má tvar ax+by+cz+d=0, kde konštanty a, b, c sú súradnice normálového vektora a d reálne číslo. Normálový vektor \vec{n}=(a;b;c) je vektor kolmý na danú rovinu.
Všeobecná rovnica roviny určenej bodom a normálovým vektorom
Určite všeobecnú rovnicu roviny \alpha určenej bodom A=[-3;1;2] a normálovým vektorom \vec{n}=(2;3;-4).
- Súradnice normálového vektora sú konštanty a, b, c vo všeobecnej rovnici roviny, preto všeobecná rovnica bude mať tvar: 2x+3y-4z+d=0
- Konštantu d určíme dosadením súradníc bodu A=[-3;1;2] do všeobecnej rovnice: 2\cdot(-3)+3\cdot1-4\cdot 2+d=0\Rightarrow -11+d=0\Rightarrow d=11
- Všeobecná rovnica roviny \alpha je: 2x+3y-4z+11=0
Všeobecná rovnica roviny danej bodom a rovnobežnej s inou rovinou
Všeobecná rovnica roviny \alpha, ktorá prechádza bodom A=[2;3;1] a je rovnobežná s rovinou \beta:3x+y+4z+1=0.
- Dve rovnobežné roviny majú rovnaký normálový vektor, súradnice normálového vektoru sú súradnice a, b, c vo všeobecnej rovnici roviny.
- Preto všeobecná rovnica hľadanej roviny \alpha bude mať tvar: 3x+y+4z+d=0
- Konštantu d určíme dosadením súradníc bodu A=[2;3;1] do všeobecnej rovnice: 3\cdot2+3+4\cdot 1+d=0\Rightarrow 13+d=0\Rightarrow d=-13
- Všeobecná rovnica roviny \alpha je: 3x+y+4z-13=0
Vzájomná poloha bodu a roviny
Bod leží v rovine, ak jeho súradnice vyhovujú rovnici roviny. Ak je rovina daná všeobecnou rovnicou, po dosiahnutí súradnic bodu do rovnice roviny nastane rovnosť. Ak je rovina daná parametricky, po dosiahnutí súradníc bodu dostaneme sústavu troch rovníc pre dve neznáme, ktorá má presne jedno riešenie.
Bod a rovina daná všeobecnou rovnicou
Určite, či body A=[3;4;2] a B=[1;3;0] ležia v rovine \alpha danej všeobecnou rovnicou 2x-y+3z+1=0.
- Do rovnice roviny dosadíme súradnice bodu A=[3;4;2].
- 2\cdot 3-4+3\cdot2+1=0\Rightarrow9\neq 0, teda bod A neleží v rovine \alpha.
- Do rovnice priamky dosadíme súradnice bodu B=[1;3;0].
- 2\cdot 1-3+3\cdot0+1=0\Rightarrow0=0, teda bod B leží v rovine \alpha.
Bod a rovina daná parametricky
Určite, či body A=[2;3;4] a B=[0;2;2] ležia v rovine \alpha danej parametrickými rovnicami:
\begin{array}{rrl}x&=&1-t+s\\y&=&2+t+s\\z&=&3-t+s\\&&t,s\in\mathbb{R}\end{array}
- Do rovníc roviny dosadíme súradnice bodu A=[1;3;4]: \begin{array}{rrrr}2&=&1-t+s\\3&=&2+t+s\\4&=&3-t+s\\\end{array}
- Z prvých dvoch rovníc určíme hodnoty t a s, dosadením do tretej rovnice zistíme, či sú nájdené hodnoty riešením sústavy a teda či bod leží na priamke:
- prvú a druhú rovnicu sčítame: 5=3+2s\Rightarrow s=1
- hodnotu s=1 dosadíme do prvej rovnice: 1=1-t+1\Rightarrow t=1
- hodnoty s=1 a t=1 dosadíme do tretej rovnice: 4=3-1+1. Táto rovnosť neplatí, teda bod A neleží v rovine \alpha.
- Do rovníc roviny dosadíme súradnice bodu B=[0;-3;2]: \begin{array}{rrrr}0&=&1-t+s\\-3&=&2+t+s\\2&=&3-t+s\\\end{array}
- Z prvých dvoch rovníc určíme hodnoty t a s, dosadením do tretej rovnice zistíme, či sú nájdené hodnoty riešením sústavy a teda či bod leží na priamke:
- prvú a druhú rovnicu sčítame: -3=3+2s\Rightarrow s=-3
- hodnotu s=-3 dosadíme do prvej rovnice: 0=1-t-3\Rightarrow t=-2
- hodnoty s=-3 a t=-2 dosadíme do tretej rovnice: 2=3-(-2)-3. Táto rovnosť platí, teda bod B leží v rovine \alpha.
Kužeľosečky
Ako už názov napovedá, majú kužeľosečky spoločný pôvod. Vzniknú ako rez rotačnej kužeľovej plochy rovinou. 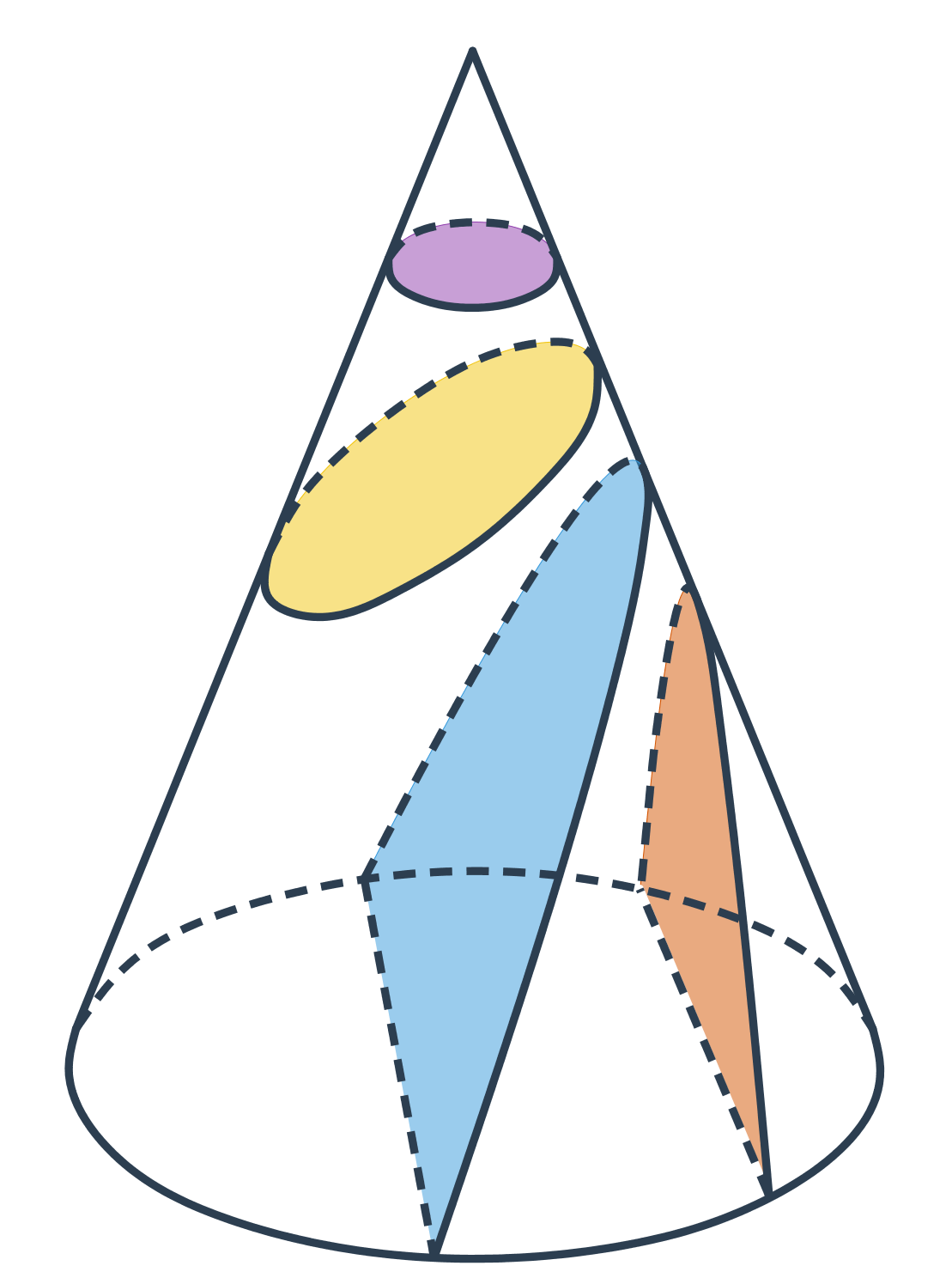
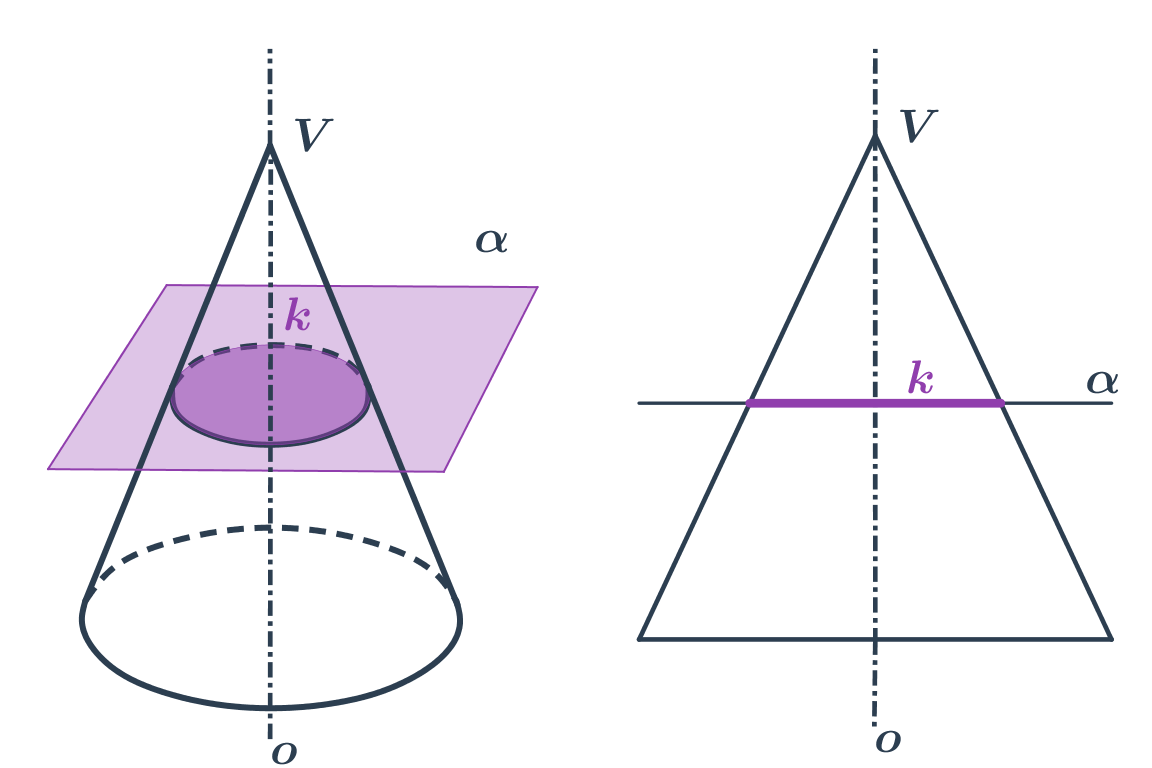
- Kružnica vznikne rezom roviny kolmej na os kužeľovej plochy.
- Ak rovinu rezu trochu nakloníme, vznikne elipsa.
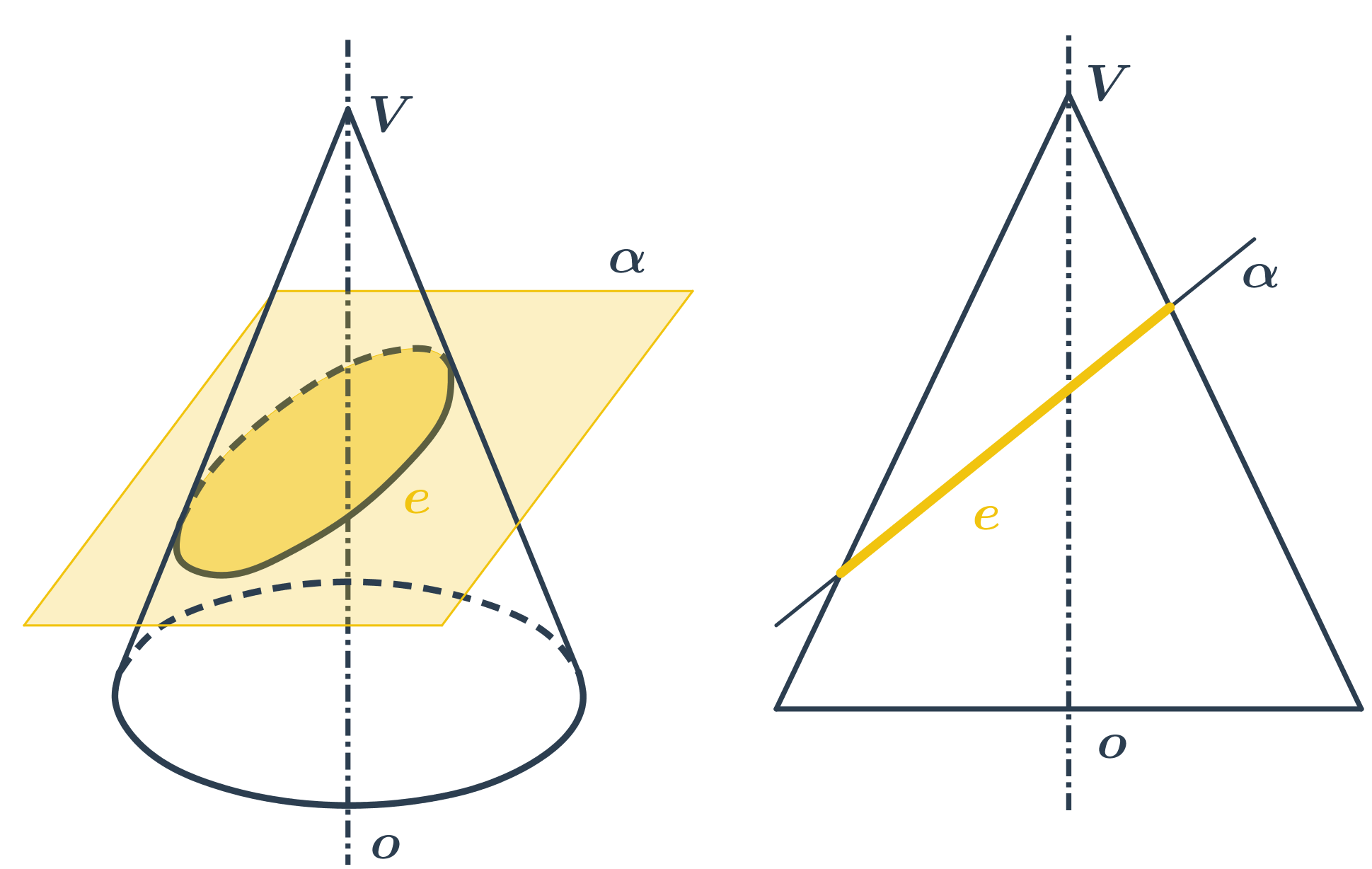
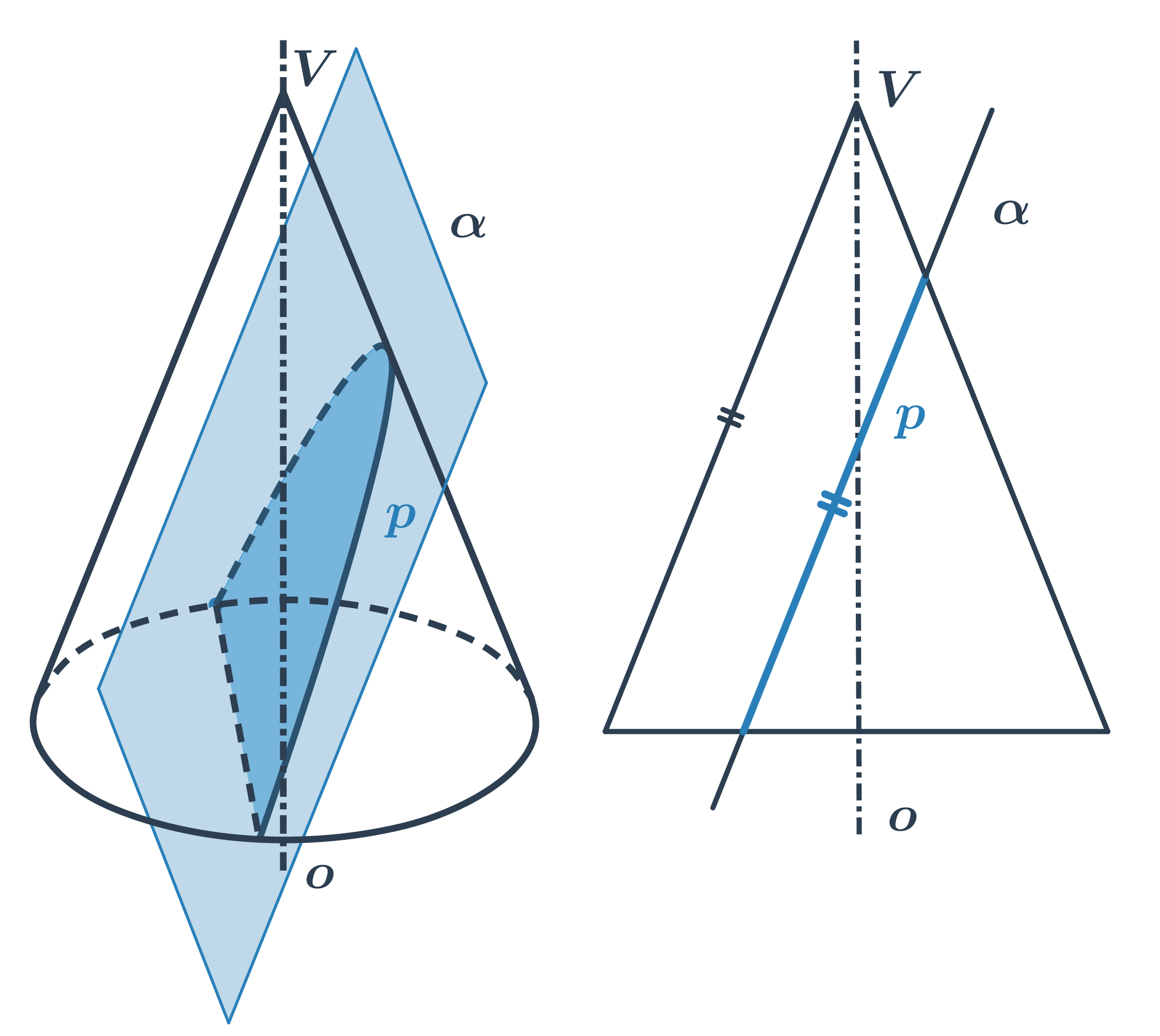
- Ak rovinu rezu nakloníme toľko, že bude rovnobežná s niektorou z priamok na kužeľovej ploche, vznikne parabola.
- Pri ďalšom nakláňaní už rovina rezu pretne obe časti kužeľovej plochy a vnikne dvojdielna hyperbola.
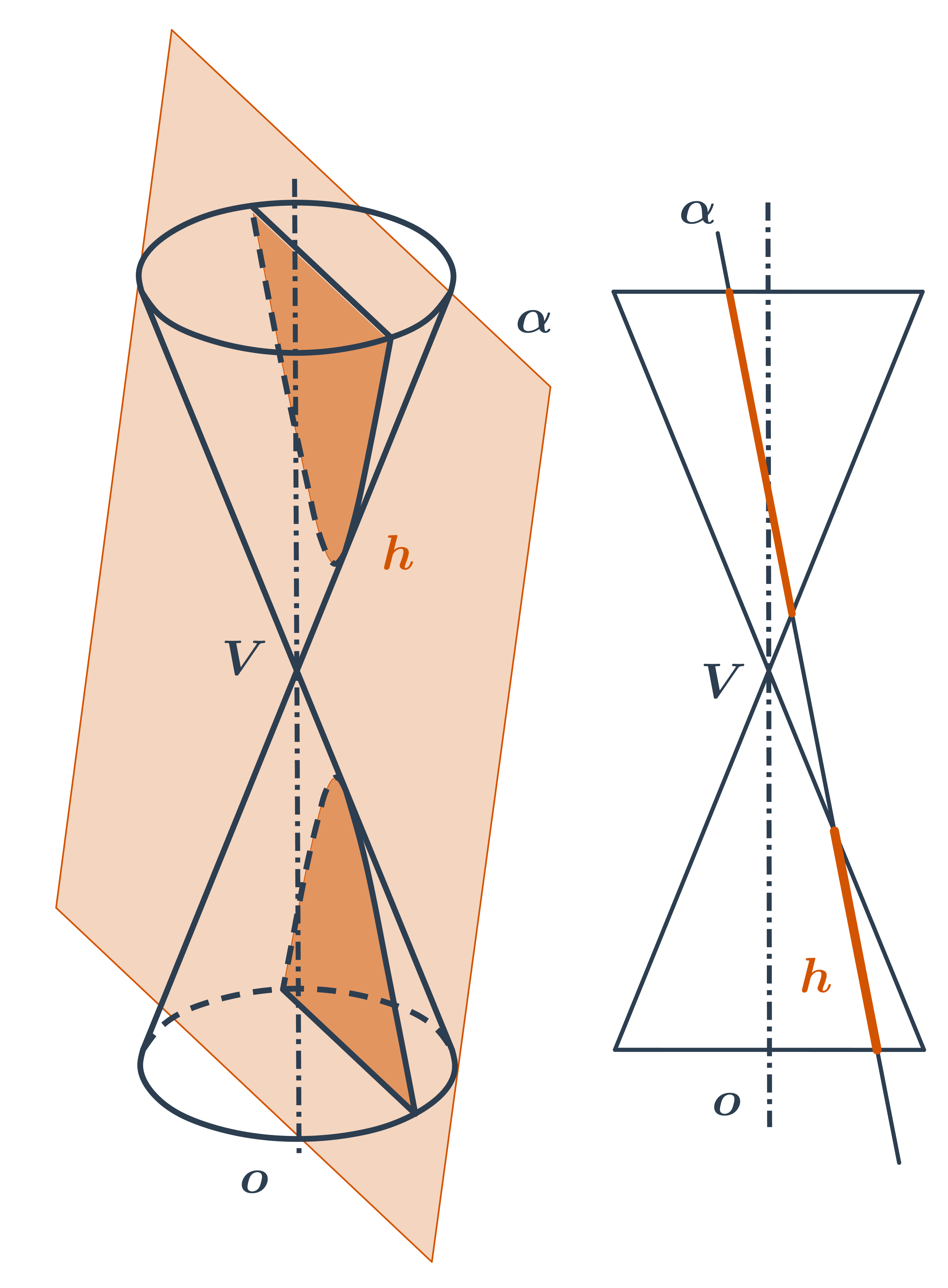
Kužeľosečky môžeme tiež chápať ako množiny bodov danej vlastnosti. V analytickej geometrii často zapisujeme tieto množiny pomocou rovníc.
HoreKružnica (kužeľosečka)
Kružnica je množina všetkých bodov v rovine, ktoré majú od daného pevného bodu S rovnakú vzdialenosť r. Bod S nazývame stred kružnice, hodnotu r nazveme polomer kružnice. 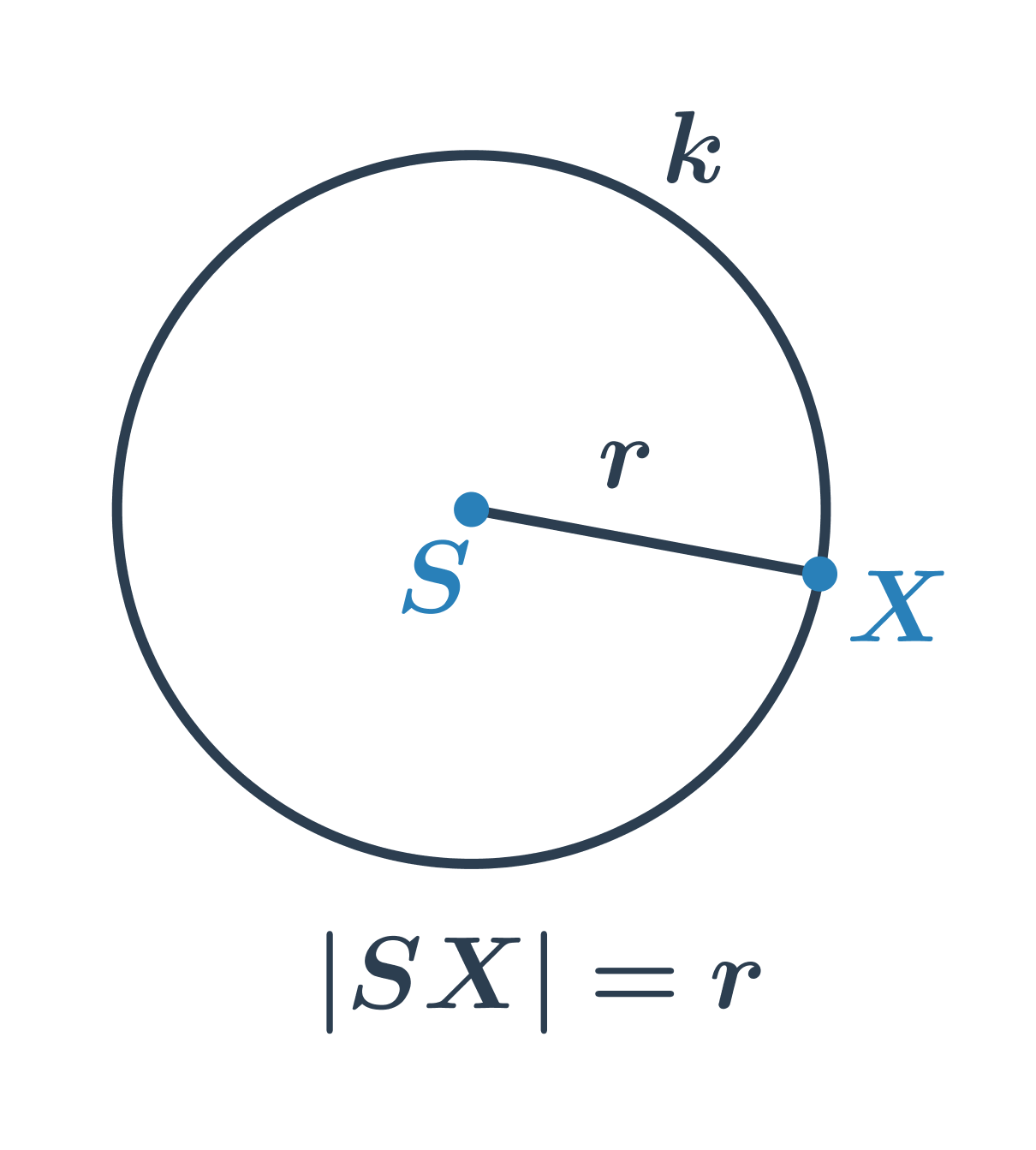
Stredová rovnica kružnice
Stredová rovnica kružnice so stredom S[m;n] a polomerom r je v tvare: (x-m)^2 +(y-n)^2=r^2 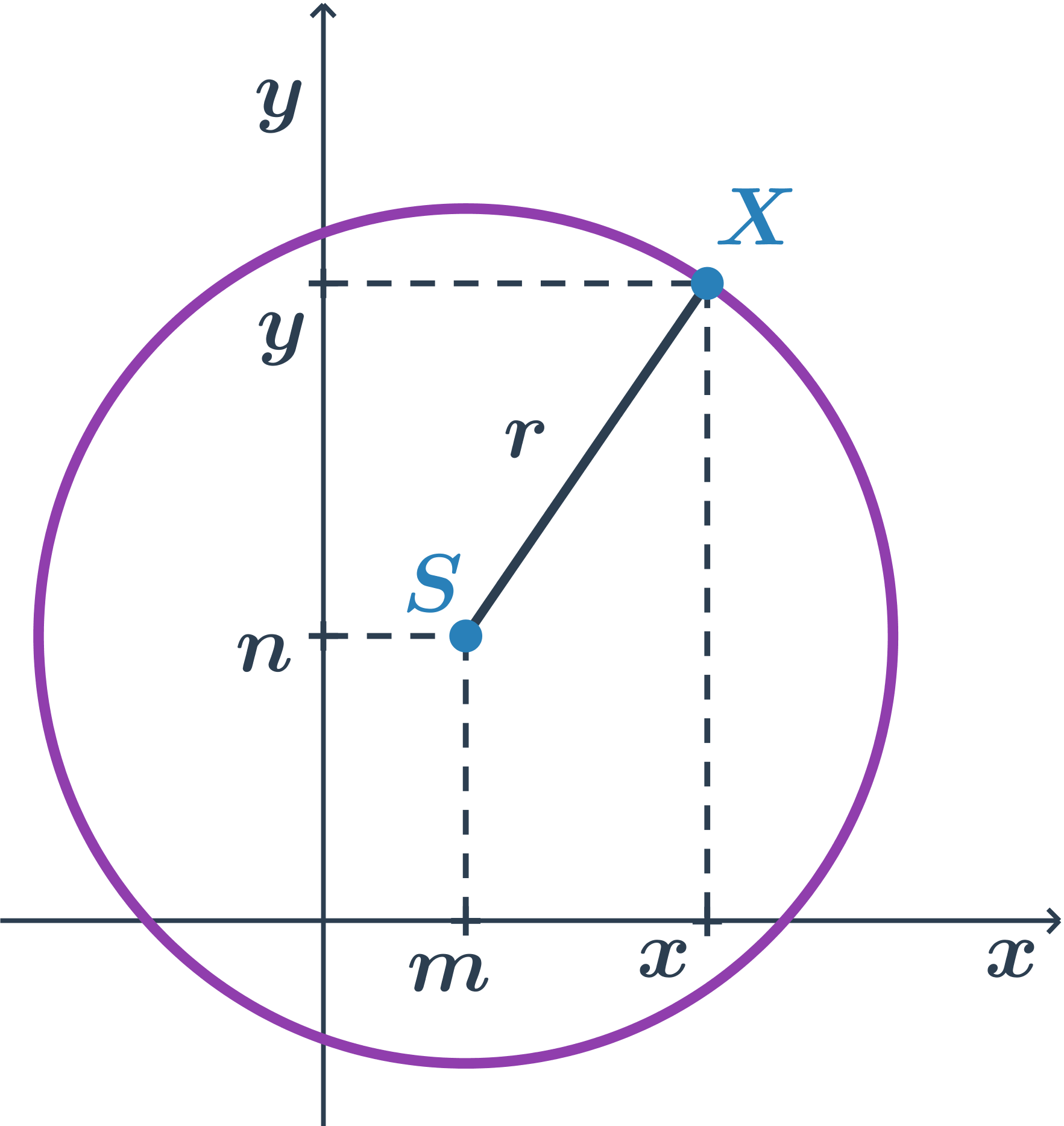
Príklad: Určite stredovú rovnicu kružnice so stredom v bode S[-1;2] a polomerom r=3.
- Stredová rovnica je v tvare: (x-m)^2 +(y-n)^2=r^2
- Dosadíme súradnice stredu a polomer. Pri dosadení si dáme pozor na to, že súradnice stredu v stredovej rovnici odčítame: (x-(-1))^2 +(y-2)^2=3^2
- Po úprave: (x+1)^2 +(y-2)^2=9
Všeobecná rovnica kružnice
Podobne ako existuje niekoľko tvarov rovníc priamky, môžeme aj rovnicu kružnice zapísať rôznymi spôsobmi. Všeobecná rovnica kružnice je v tvare: x^2 +y^2-2mx-2ny+p=1.
Každá rovnica v tomto tvare ale nemusí ešte byť všeobecnou rovnicou kružnice. Pre všeobecnú rovnicu kružnice musí platiť, že výraz m^2+n^2-p je kladný. Praktické overenie, či ide o kružnicu, ale väčšinou vykonávame prevedením na stredovú rovnicu kružnice.
Príklad: Nájdite stred a polomer kružnice danej všeobecnou rovnicou x^2+y^2+4x+6y-12=0.
- Najskôr si usporiadame členy podľa premenných: x^2+4x+y^2-6y-12=0.
- Našim ďalším cieľom je upraviť výraz na ľavej strane ako súčet dvoch druhých mocnín (štvorcov), podľa vzorcov a^2\pm 2ab+b^2=(a\pm b)^2.
- K obom stranám rovnice pripočítame konštanty 4 a 9, aby sme súčty členov s premennými x a y mohli upraviť na druhé mocniny (prevedieme v oboch prípadoch doplnenie na štvorec): x^2+4x+4+y^2-6y+9-12=4+9
- A upravíme: (x+2)^2 +(y-3)^2-12=13
- Na záver ešte prevedieme -12 na druhú stranu rovnice: (x+2)^2 +(y-3)^2=25
- Týmto sme previedli všeobecnú rovnicu kružnice na stredovú rovnicu kružnice.
- Polomer kružnice je r=\sqrt{25}=5.
- Súradnice stredu S[m,n] odčítame v stredovej rovnici od premenných x a y, majú teda opačné znamienka než konštanty v zátvorkách v stredovej rovnici \Rightarrow S[-2;3].
Kružnica a priamka
- priamka s pretína kružnicu v dvoch bodoch – sečnica kružnice
- priamka t pretína kružnicu v jednom bode – dotyčnica kružnice
- priamka v kružnici nepretína – vonkajšia priamka kružnice
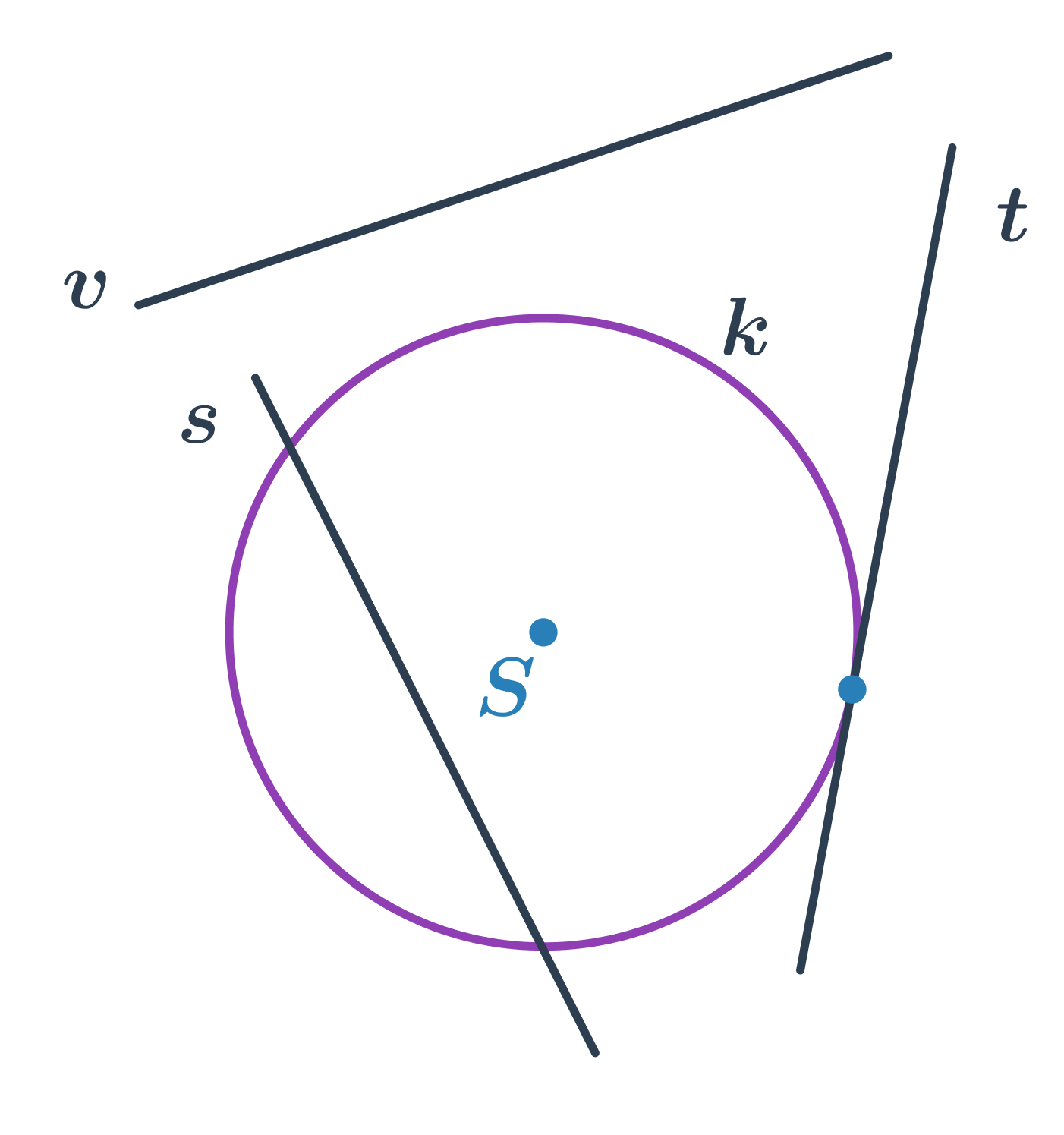
Rovnice dotyčnice kružnice v bode, ktorý leží na kružnici
Kružnica daná rovnicou (x-m)^2 +(y-n)^2=r^2 má v bode T[x_0;y_0] dotyčnicu (x_0-m)(x-m) +(y_0-n)(y-n)=r^2.Ako si zapamätať rovnicu dotyčnice
- Stredová rovnica je v tvare (x-m)^2 +(y-n)^2=r^2.
- Zátvorky rozložíme na súčiny dvojčlenov (x-m)(x-m) +(y-n)(y-n)=r^2.
- V každom súčine zameníme jedno x za x_0 a jedno y za y_0
- Dostaneme rovnicu dotyčnice (x_0-m)(x-m) +(y_0-n)(y-n)=r^2
Príklad: Určite rovnicu dotyčnice kružnice (x-1)^2+(y+2)^2=13 v jej bode T[3;1].
- Overíme, či bod T leží na kružnici: (3-1)^2+(1+2)^2=13 \Rightarrow 4+9=13
- Dotyčnica má rovnicu (x_0-m)(x-m) +(y_0-n)(y-n)=r^2
- Dosadíme súradnice bodu T: (3-1)(x-1) +(1+2)(y+2)=13
- Roznásobíme zátvorky: 2x-2 +3y+6=13
- A dostaneme všeobecnú rovnicu dotyčnice 2x+3y-9=0
Polára kružnice
Z bodu R mimo kružnicu môžeme zostrojiť dve dotyčnice k danej kružnici. Priamka určená bodmi dotyku dotyčníc sa nazýva polára kružnice vzhľadom k bodu R. 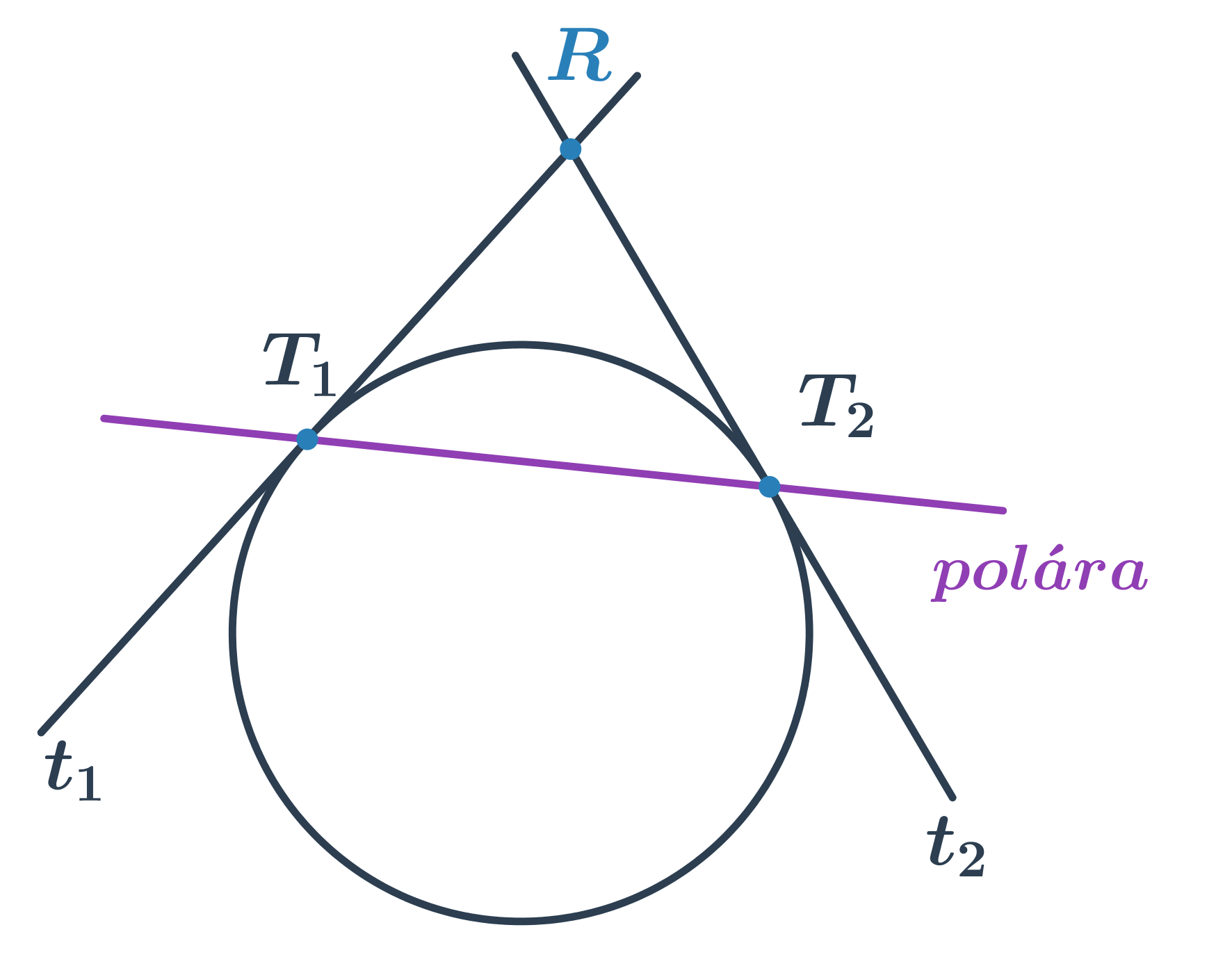
Rovnica poláry kružnice (x-m)^2 +(y-n)^2=r^2 vzhľadom k bodu R[r_1;r_2] je (r_1-m)(x-m) +(r_2-n)(y-n)=r^2.
Na čo poláru použijeme?
- Poláru využívame na konštrukciu dotyčníc ležiacich z bodu mimo kružnicu.
- Podľa vzorca určíme rovnicu poláry, teda priamky.
- Nájdeme priesečníky poláry a kružnice – to sú body dotyku hľadaných dotyčníc.
- Keď poznáme body dotyku, určíme podľa vzťahu pre rovnicu dotyčnice v bode kružnice všeobecné rovnice oboch dotyčníc.
Elipsa je množina všetkých bodov v rovine, ktoré majú od dvoch rôznych bodov (ohnísk) stály súčet vzdialeností 2a, ktorý je väčší než vzdialenosť ohnísk.
Stredová rovnica elipsy
Tvar stredovej rovnice elipsy so stredom S[m;n] s veľkosťami hlavnej a vedľajšej polosi a a b závisí od polohy hlavnej osi:
hlavná os je rovnobežná s osou x, rovnica je v tvare: \frac{(x-m)^2}{a^2} +\frac{(y-n)^2}{b^2}=1
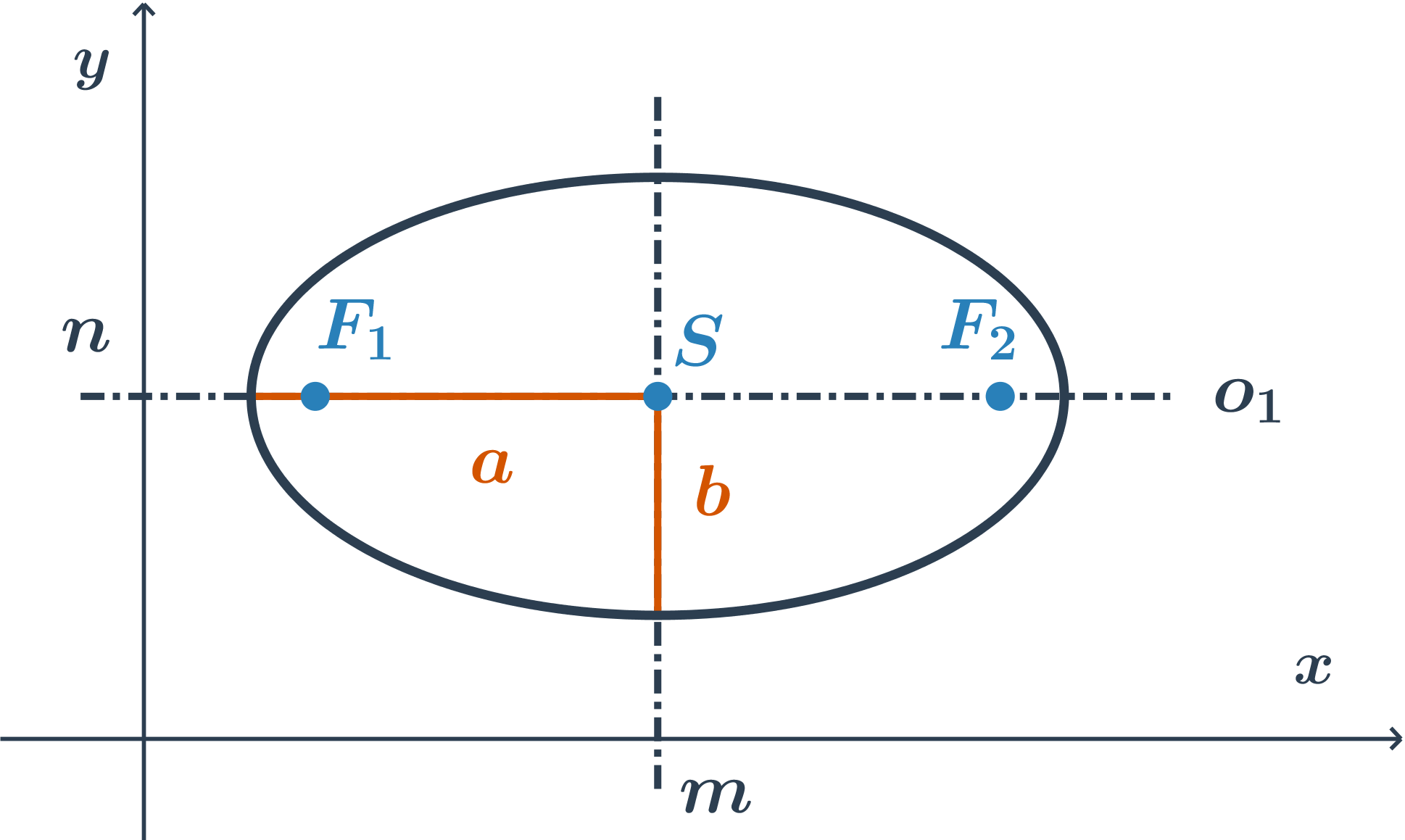
hlavná os je rovnobežná s osou y, rovnica je v tvare: \frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1
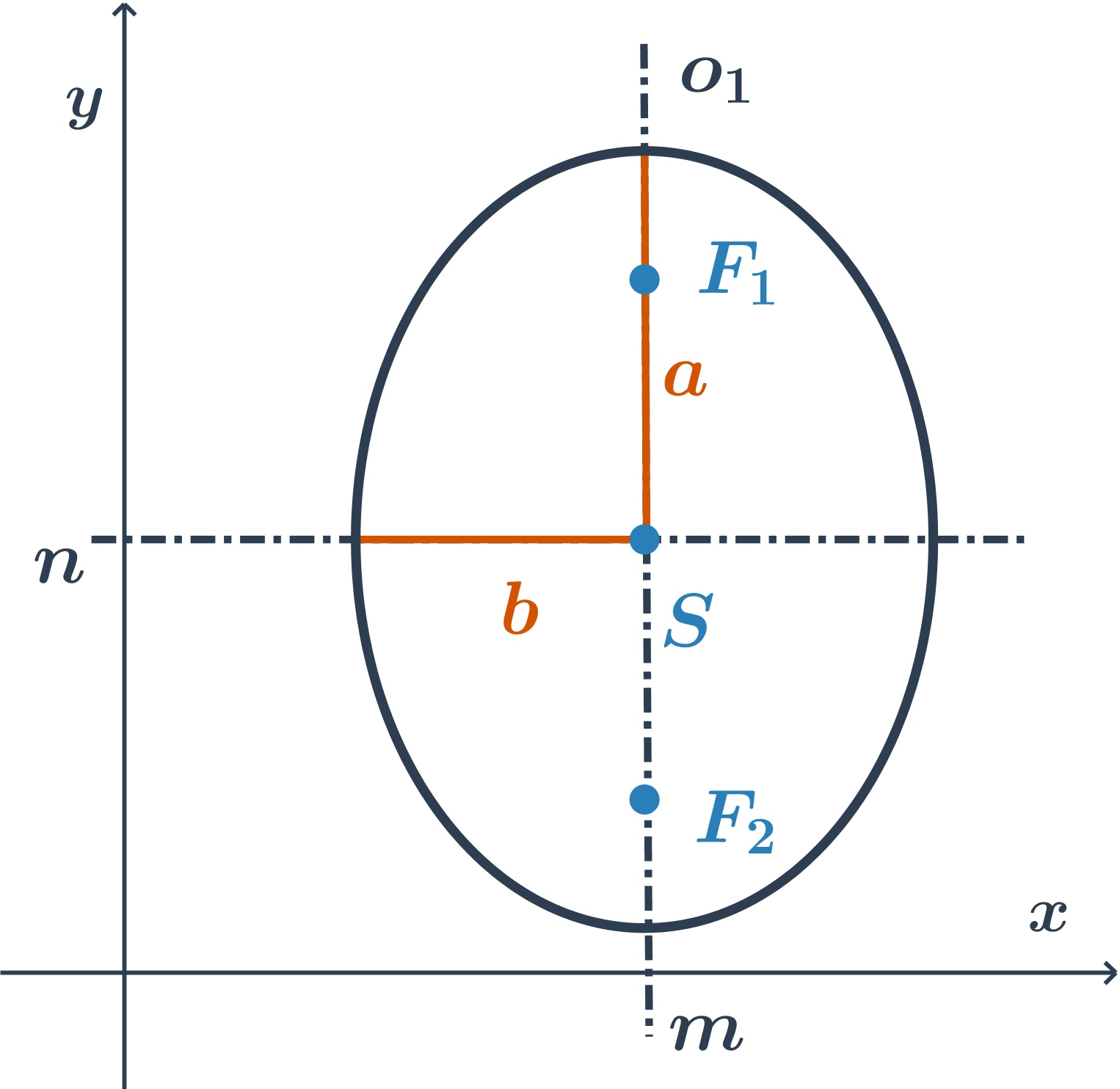
Návod: ako z rovnice zistiť, s ktorou súradnicovou osou je rovnobežná hlavná os elipsy
- Pozrieme sa do menovateľov.
- Väčší menovateľ je druhá mocnina veľkosti hlavnej polosi (a menší menovateľ je druhá mocnina veľkosti vedľajšej polosi).
- Premenná v danom čitateli (zlomku s väčším menovateľom) potom určuje, s ktorou osou je hlavná os elipsy rovnobežná.
- Stručne povedané: ak je väčšie číslo napríklad v menovateli s premennou x, je hlavná os rovnobežná s osou x.
Príklad: určenie stredovej rovnice elipsy s daným stredom, veľkosťami polosí a smerom hlavnej osi
Určite stredovú rovnicu elipsy so stredom v bode S[-2;3], je‑li a=3, b=2 ak hlavná os je rovnobežná s osou y.
- Stredová rovnica je v tvare \frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1.
- Dosadíme súradnice stredu a veľkosti hlavnej a vedľajšej polosi. Pri dosadení si dáme pozor na to, že súradnice stredu odčítame: \frac{(x-(-2))^2}{2^2} +\frac{(y-3)^2}{3^2}=1
- Po úprave: \frac{(x+2)^2}{4} +\frac{(y-3)^2}{9}=1
Všeobecná rovnica elipsy
Podobne ako existuje niekoľko rovníc priamky, môžeme aj rovnicu elipsy zapísať iným spôsobom. Všeobecná rovnica elipsy je v tvare:
Ax^2 +By^2+Cx+Dy+E=1, A\ne B, A\cdot B>0.
Každá rovnica v tomto tvare ale nemusí byť všeobecnou rovnicou elipsy. Praktické overenie, či ide o elipsu vykonávame prevedením na stredovú rovnicu.
Príklad: určuje daná rovnica elipsu?
Rozhodnite, či rovnica x^2+3y^2+8x-18y+31=0 určuje elipsu.
- Najskôr si usporiadame členy: x^2+8x+3y^2-18y+31=0.
- Z členov s premennou y vytkneme 3: x^2+8x+3(y^2-6y)+31=0
- K obom stranám rovnice pripočítame konštanty 16 a 27, aby sme členy s premennými x a y mohli upraviť podľa vzťahu (a\pm b)^2=a^2 \pm 2ab +b^2.
- Máme: x^2+8x+16+3(y^2-6y+9)+31=16+27
- A upravíme: (x+4)^2 +3(y-3)^2+31=43
- Prevedieme konštantu 31 na druhú stranu rovnice: (x+4)^2 +3(y-3)^2=12
- Na záver rovnicu vydelíme 12: \frac{(x+4)^2}{12} +\frac{(y-3)^2}{4}=1
- Ide teda o elipsu.
Elipsa a priamka
- priamka s pretína elipsu v dvoch bodoch – sečnica elipsy
- priamka t pretína elipsu v jednom bode – dotyčnica elipsy
- priamka v elipsu nepretína – vonkajšia priamka elipsy
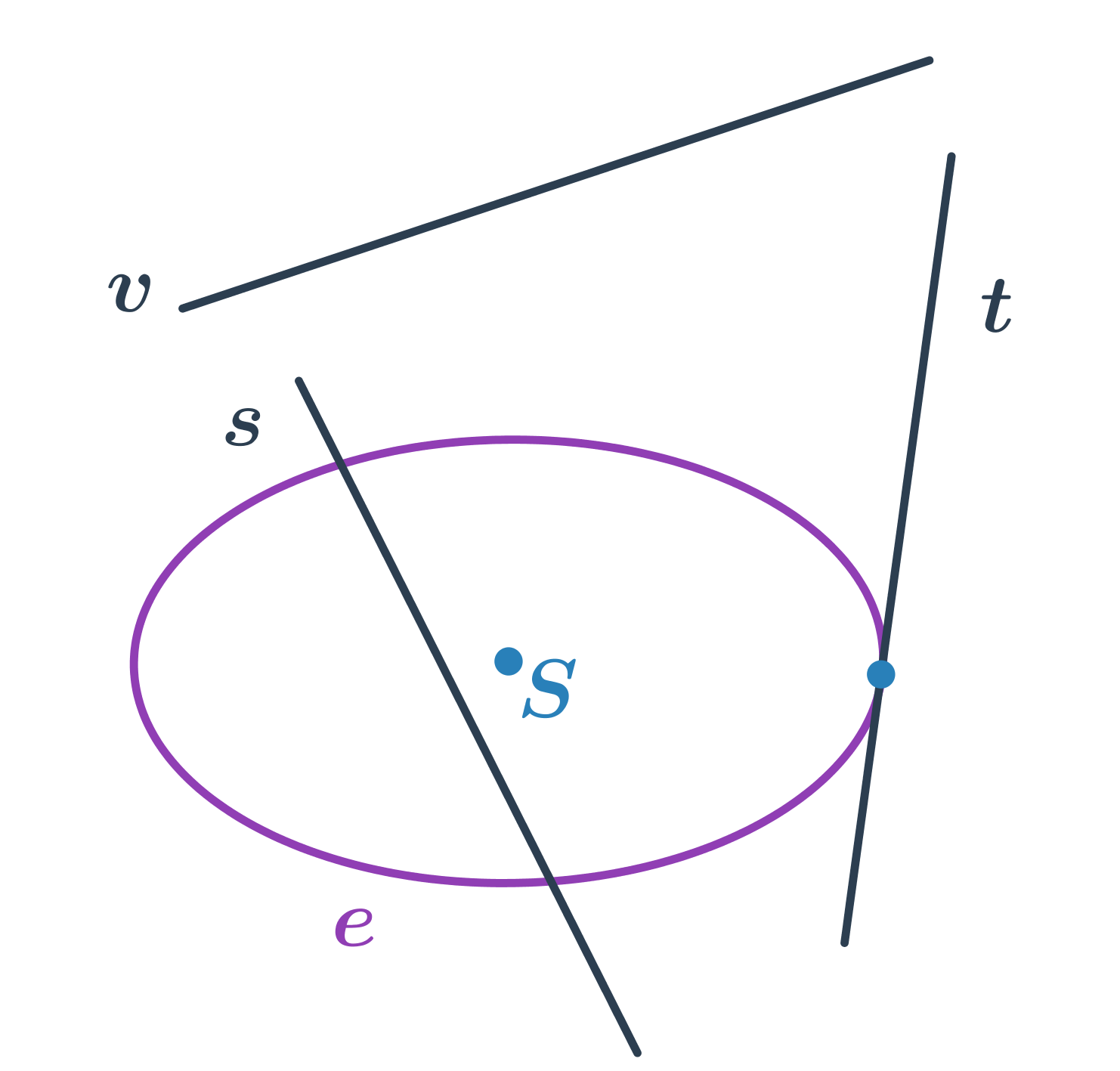
Rovnice dotyčnice elipsy v bode, ktorý leží na elipse
Elipsa daná rovnicou \frac{(x-m)^2}{a^2} +\frac{(y-n)^2}{b^2}=1 má v bode T[x_0;y_0] dotyčnicu určenú rovnicou:
\frac{(x-m)(x_0-m)}{a^2} +\frac{(y-n)(y_0-n)}{b^2}=1
Podobne môžeme zapísať aj rovnicu dotyčnice elipsy, ktorá má hlavnú os rovnobežnú s osou y.
Príklad: určenie rovnice dotyčnice elipsy v jej danom bode
Určite rovnicu dotyčnice elipsy \frac{(x-2)^2}{9} +\frac{(y-2)^2}{18}=1 v jej bode T[1;-2].
- Overíme, či bod T leží na elipse: \frac{(1-2)^2}{9} +\frac{(-2-2)^2}{18}=1 \Rightarrow \frac19+\frac{16}{18}=1 \Rightarrow 1=1
- Dotyčnica má rovnicu \frac{(x-m)(x_0-m)}{b^2} +\frac{(y-n)(y_0-n)}{a^2}=1
- Dosadíme súradnice bodu T: \frac{(x-2)(1-2)}{9} +\frac{(y-2)(-2-2)}{18}=1
- Zbavíme sa zlomkov: 2(x-2)\cdot(-1) +(y-2)\cdot(-4)=18
- Roznásobíme zátvorky: -2x+4 -4y+8=18
- A dostaneme všeobecnú rovnicu dotyčnice: x+2y+3=0
Parabola je množina všetkých bodov roviny, ktoré majú rovnakú vzdialenosť od daného bodu (ohnisko) a danej priamky (riadiaca priamka).
Vrcholová rovnica paraboly
Tvar rovnice závisí od umiestnenia osi:
- os paraboly rovnobežná s osou y, vrcholová rovnice má potom tvar: (x-m)^2=\pm 2p(y-n)
- os paraboly rovnobežná s osou x, vrcholová rovnica má potom tvar: (y-n)^2=\pm 2p(x-m)
V rovnici paraboly označujú m, n súradnice vrcholu paraboly, teda vrchol je bod V=[m;n]. Ďalej p je parameter paraboly = vzdialenosť ohniska od riadiacej priamky. Znamienko pred parametrom závisí od polohy na vrchole vzhľadom k bodom paraboly.
Príklad paraboly s osou rovnobežnou s osou y
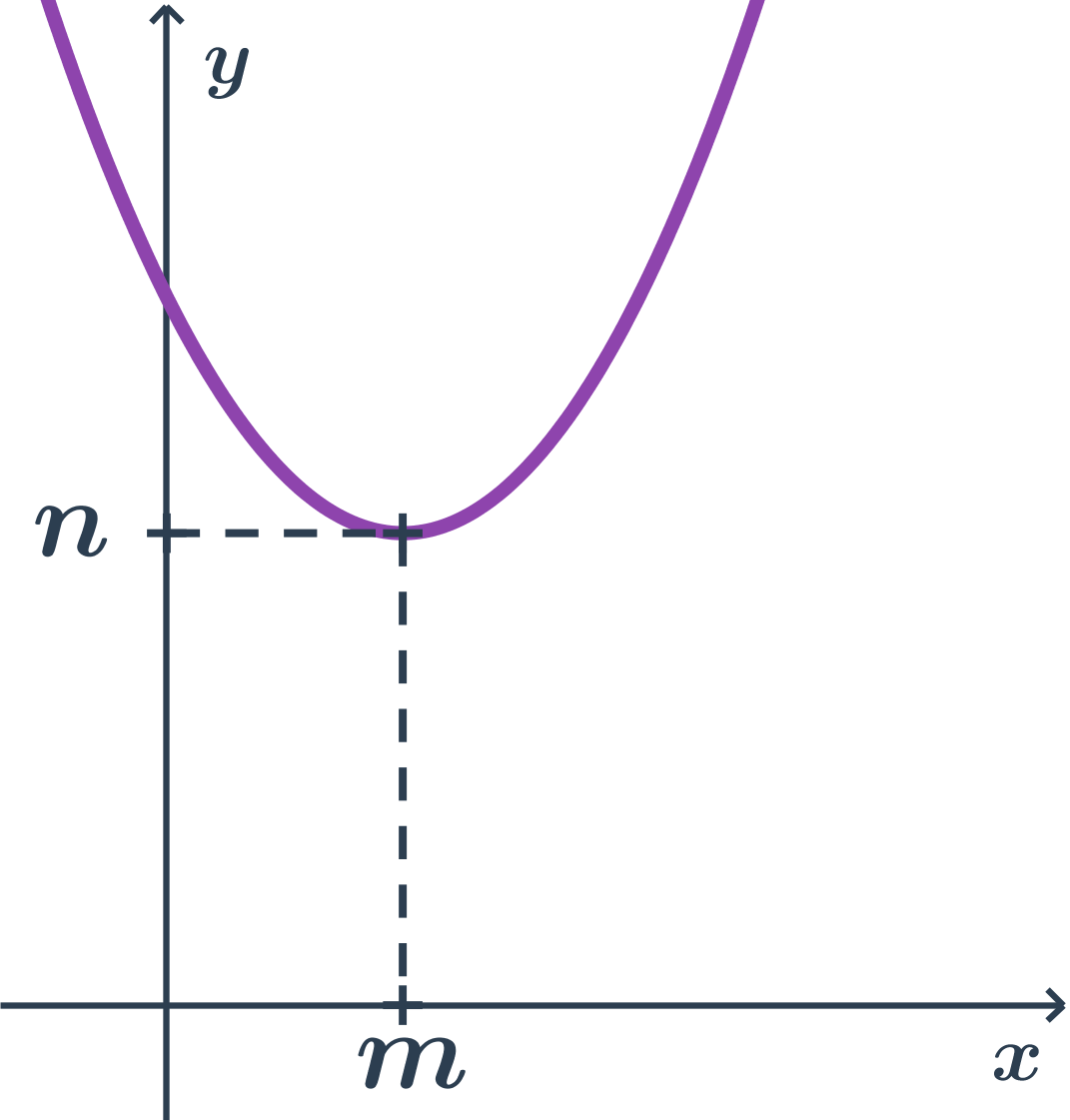
- body paraboly majú y súradnicu aspoň tak veľkú ako vrchol (teda n)
- vrcholová rovnica: (x-m)^2= + 2p(y-n)
Príklad paraboly s osou rovnobežnou s osou y, druhá orientácia
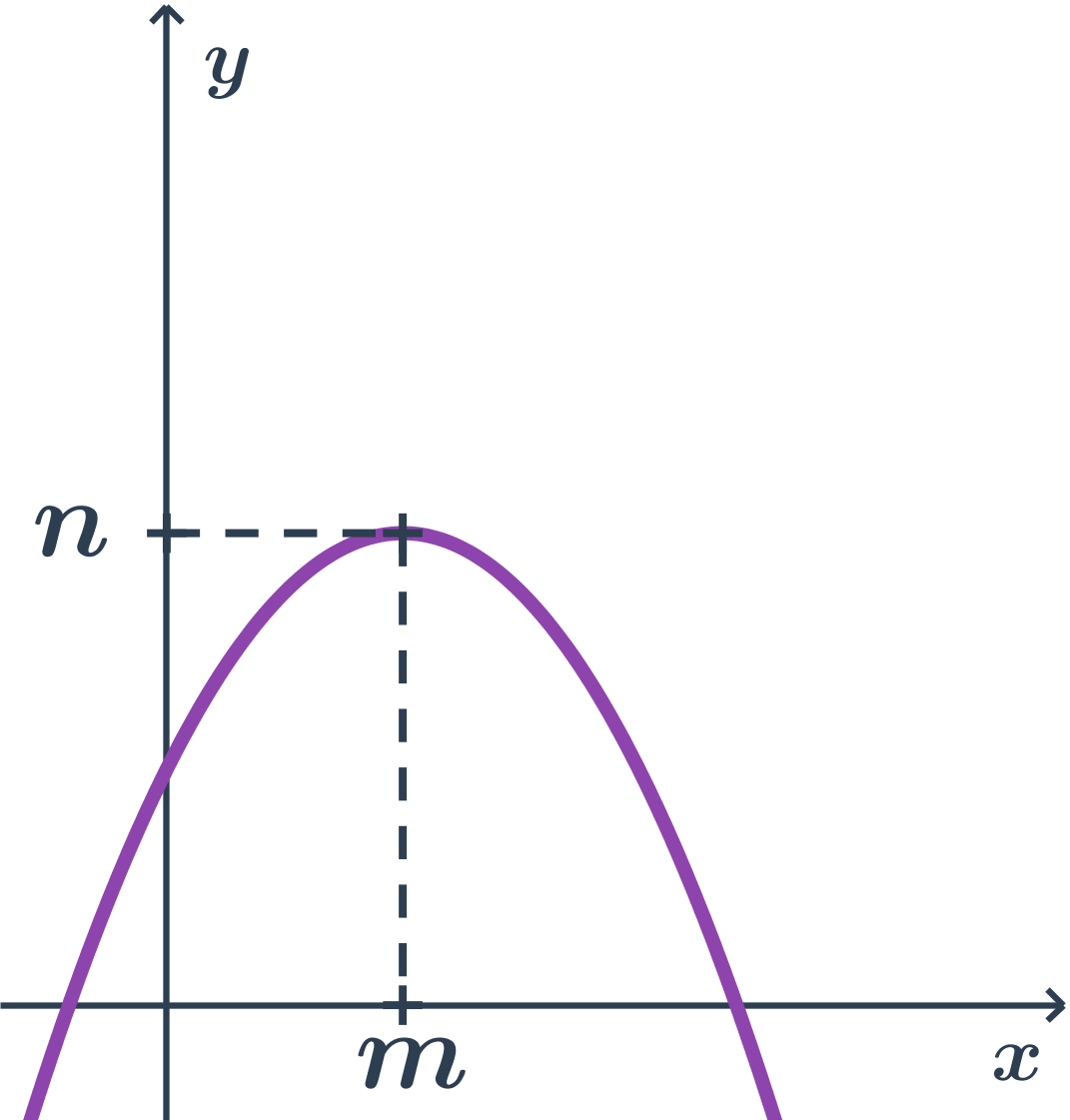
- body paraboly majú y súradnicu najviac tak veľkú ako vrchol (teda n)
- vrcholová rovnica: (x-m)^2= - 2p(y-n)
Príklad paraboly s osou rovnobežnou s osou x
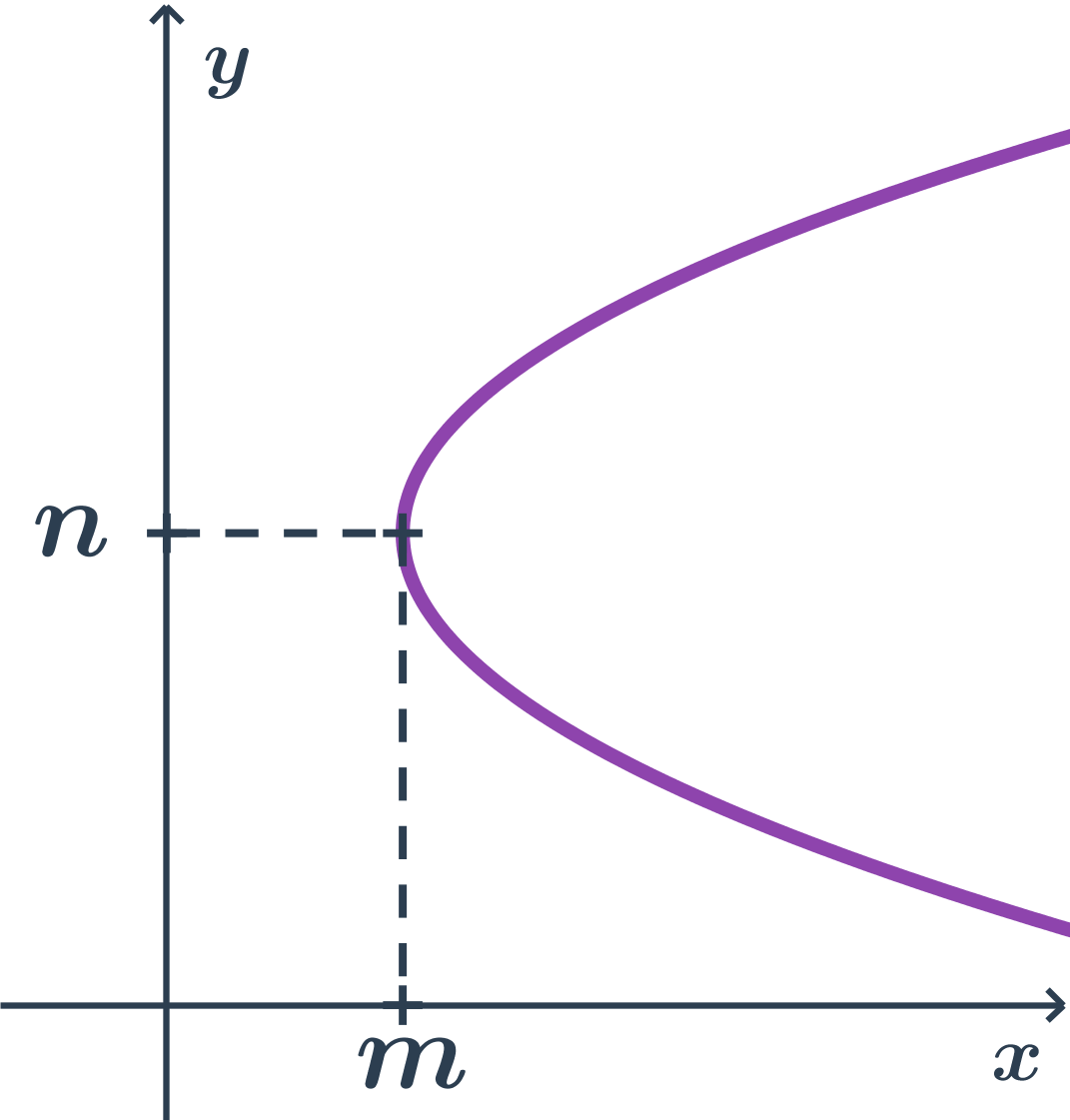
- body paraboly majú x súradnicu aspoň tak veľkú ako vrchol (teda m)
- vrcholová rovnica: (y-n)^2= + 2p(x-m)
Príklad paraboly s osou rovnobežnou s osou x, druhá orientácia
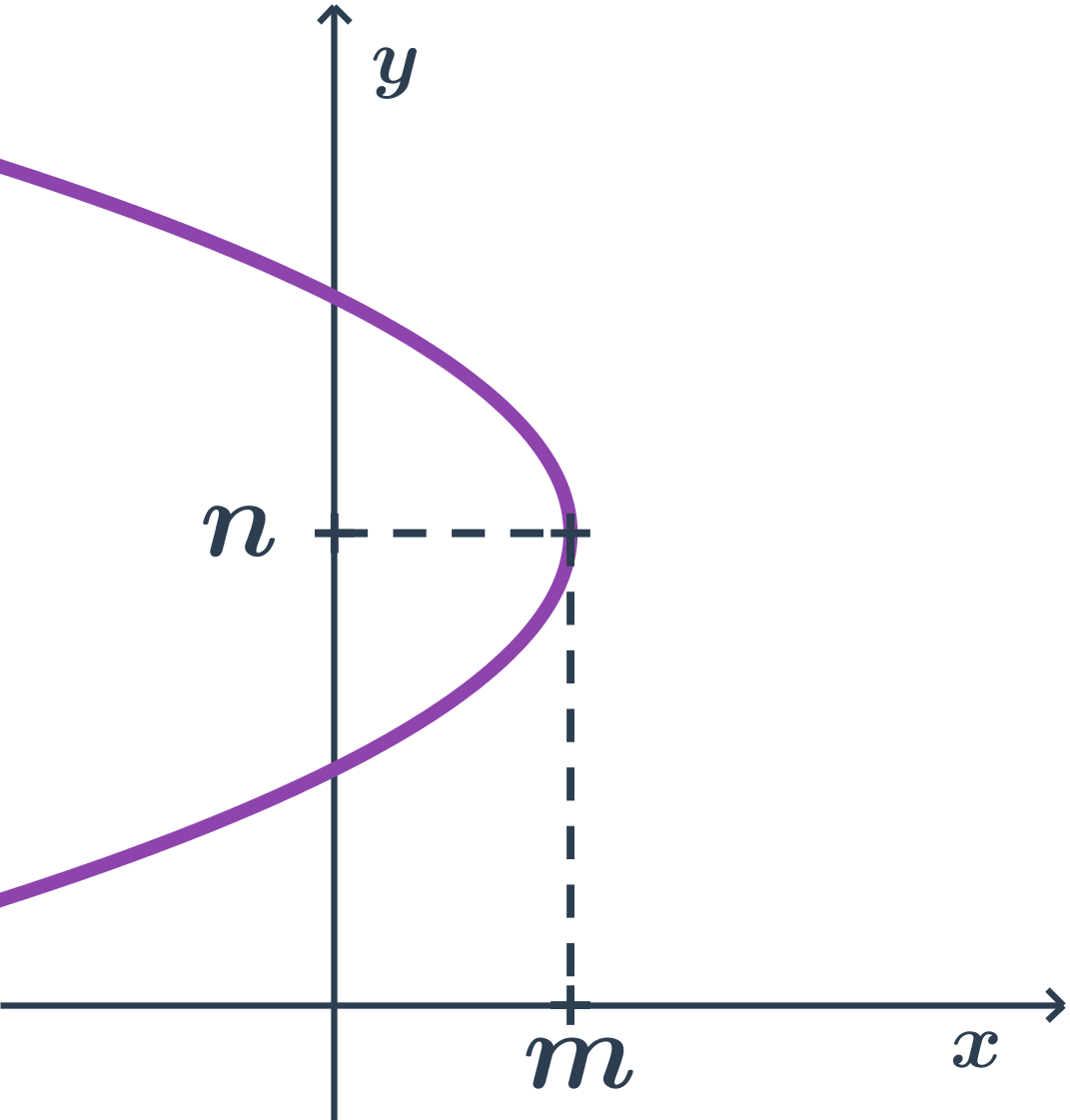
- body paraboly majú x súradnicu najviac tak veľkú ako vrchol (teda m)
- vrcholová rovnica: (y-n)^2= - 2p(x-m)
Všeobecná rovnica paraboly
Tvar rovnice závisí od umiestnenia osi:
- os paraboly je rovnobežná s osou y: y=ax^2+bx+c
- os paraboly je rovnobežná s osou x: x=ay^2+bx+c
Príklad paraboly s osou rovnobežnou s osou y, všeobecná rovnica
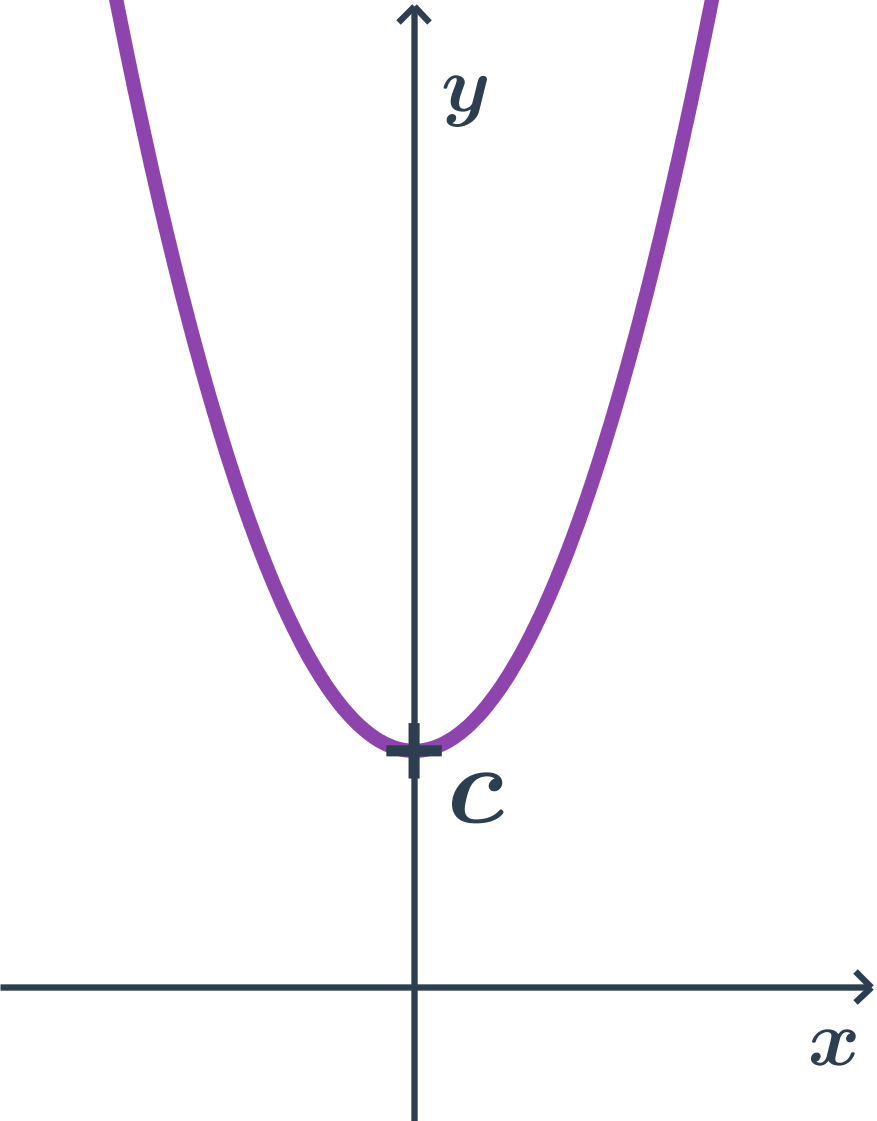
- všeobecná rovnica: y=ax^2+bx+c
- kde a>0
Príklad paraboly s osou rovnobežnou s osou y, druhá orientácia, všeobecná rovnica
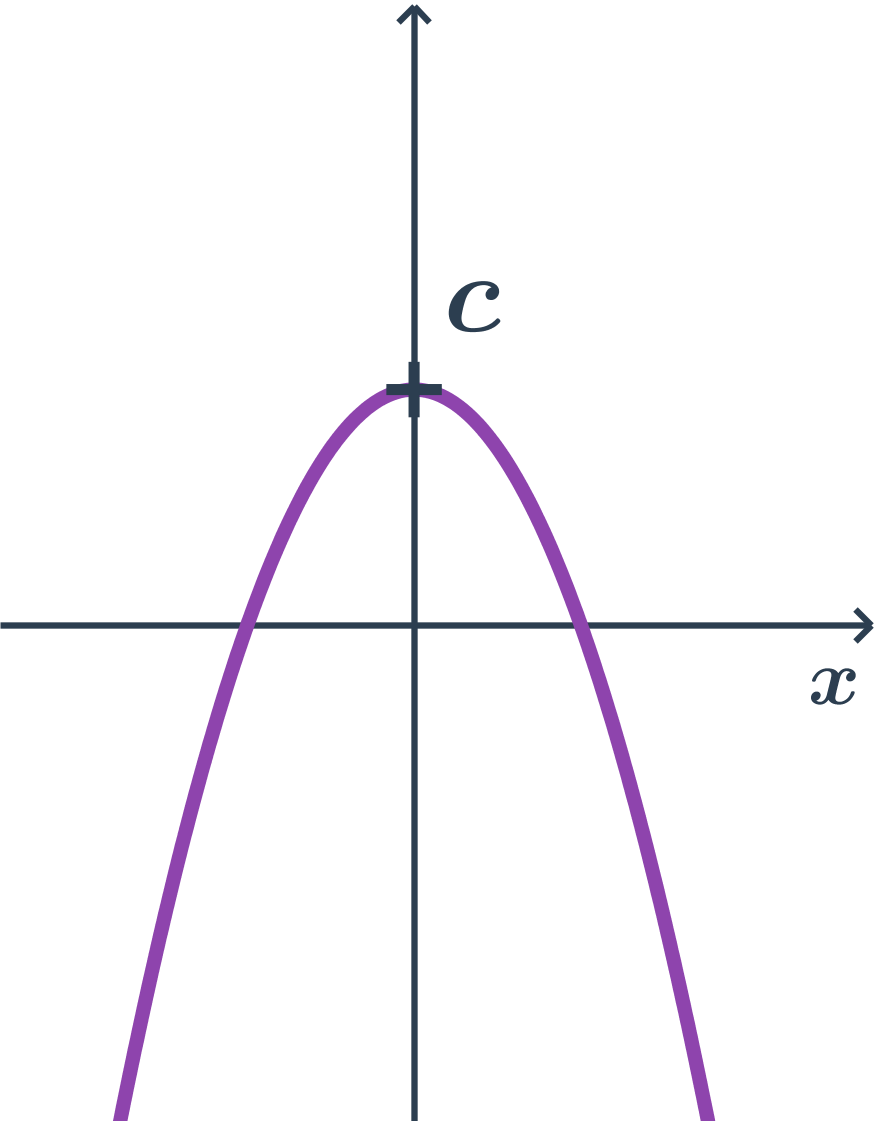
- všeobecná rovnica: y=ax^2+bx+c
- kde a < 0
Príklad paraboly s osou rovnobežnou s osou x, všeobecná rovnica
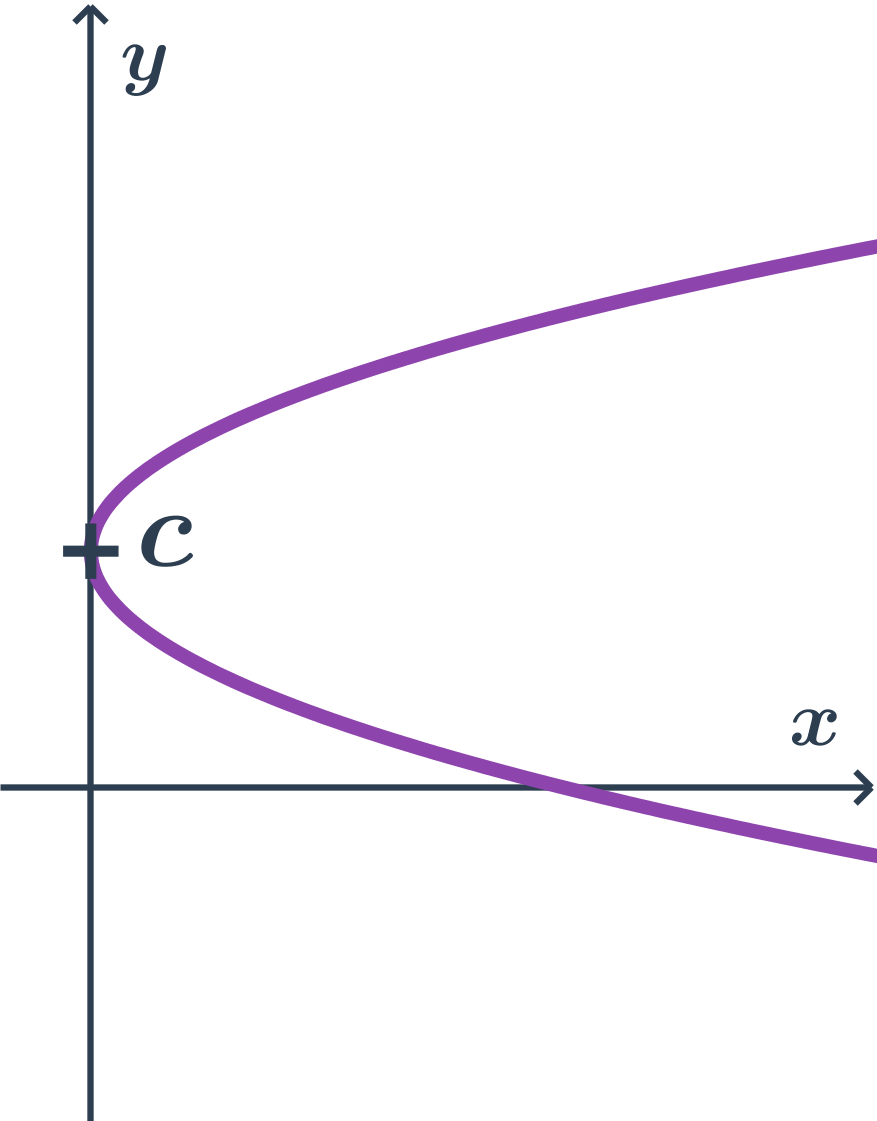
- všeobecná rovnica: x=ay^2+bx+c
- kde a > 0
Príklad paraboly s osou rovnobežnou s osou x, druhá orientácia, všeobecná rovnica
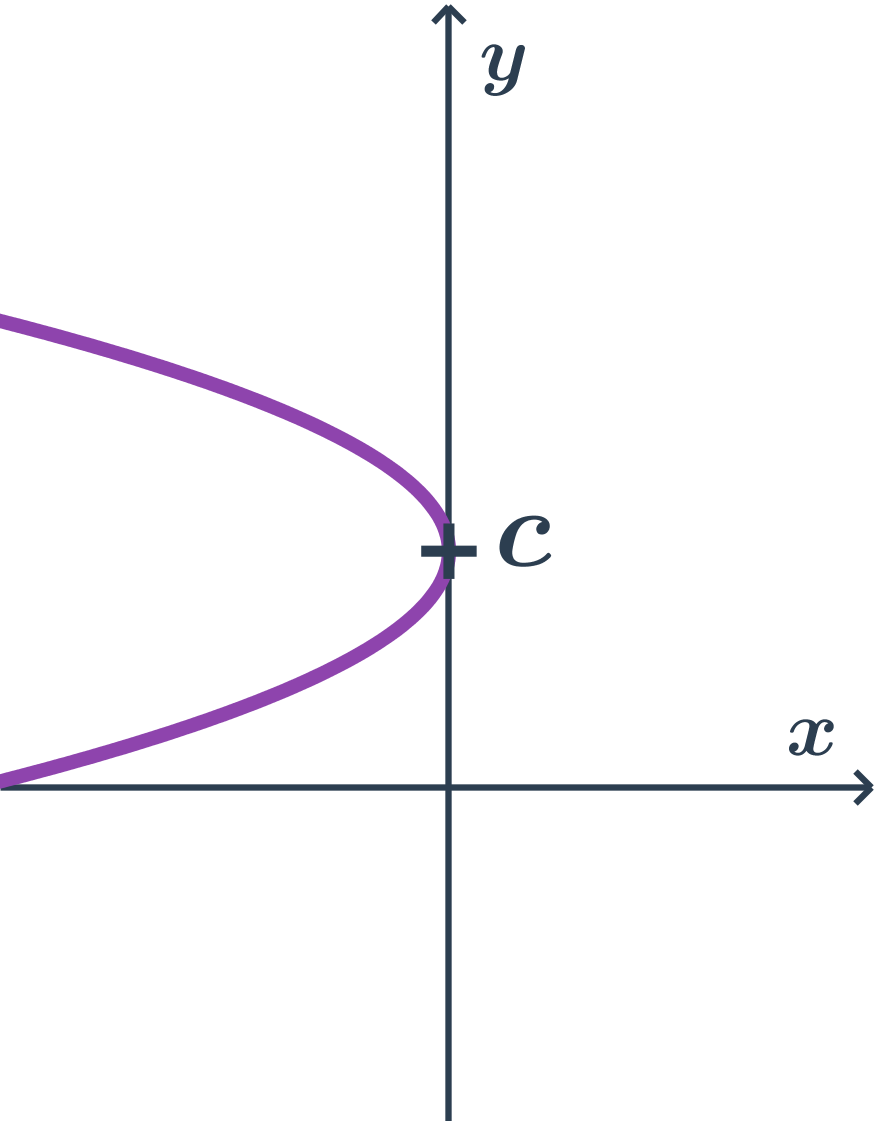
- všeobecná rovnica: x=ay^2+bx+c
- kde a < 0
Priamka a parabola
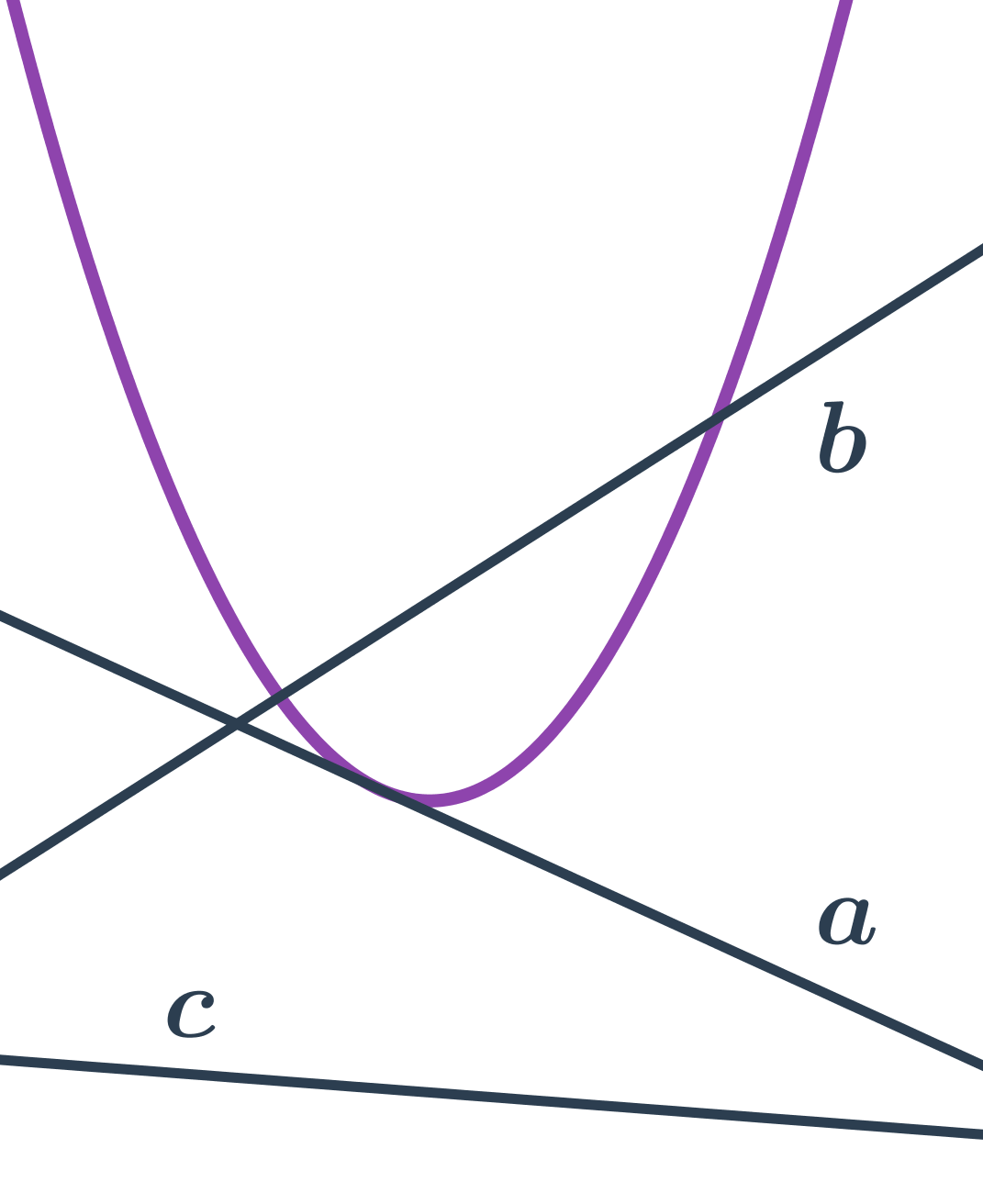
- priamka b pretína parabolu v dvoch bodoch – sečnica paraboly
- priamka a sa dotýka paraboly v jednom bode – dotyčnica paraboly
- priamka c nepretína parabolu
Rovnica dotyčnice paraboly v bode, ktorý leží na parabole
- parabola daná rovnicou (x-m)^2=\pm 2p(y-n) má v bode T=[x_0;y_0] dotyčnicu: (x-m)(x-x_0)=\pm p(y-n)\pm p(y-y_0)
- parabola daná rovnicou (y-n)^2=\pm 2p(x-m) má v bode T=[x_0;y_0] dotyčnicu: (y-n)(y-y_0)=\pm p(x-m)\pm p(x-x_0)
Príklad dotyčnice paraboly v bode
- majme parabolu danú vrcholovou rovnicou: (x-2)^2=2(y-1)
- pre túto parabolu je m=2, n=1, p=1
- na tejto parabole leží (súradnica spĺňajúca rovnicu) napríklad bod T=[4;3]
- dotyčnica danej paraboly v bode T=[4;3] má rovnicu: (x-2)(x-4)= (y-1)+(y-3)
Druhý príklad dotyčnice paraboly v bode
- majme parabolu danú vrcholovou rovnicou: (x-2)^2=-4(y-1)
- pre túto parabolu je m=2, n=1, p=2
- na tejto parabole leží (súradnice spĺňajú rovnicu) napríklad bod T=[6;-3]
- dotyčnica danej paraboly v bode T=[6;-3] má rovnicu: (x-2)(x-6)= -2(y-1)-2(y+3)
Hyperbola
Hyperbola je množina všetkých bodov v rovine, ktoré majú od dvoch rôznych bodov (ohnísk) stály rozdiel vzdialeností 2a, ktorý je menší než vzdialenosť ohnísk. Hyperbola sa skladá z dvoch častí – vetiev hyperboly. Tieto dve vetvy sa blížia k priamkam, ktoré nazývame asymptoty.
Stredová rovnica hyperboly
Tvar stredovej rovnice hyperboly so stredom S[m;n] s veľkosťami hlavnej a vedľajšej polosi a,b závisí od polohy hlavnej osi.
Stredová rovnica hyperboly s hlavnou osou rovnobežnou s osou x
Ak je hlavná os rovnobežná s osou x, rovnica je v tvare \frac{(x-m)^2}{a^2} -\frac{(y-n)^2}{b^2}=1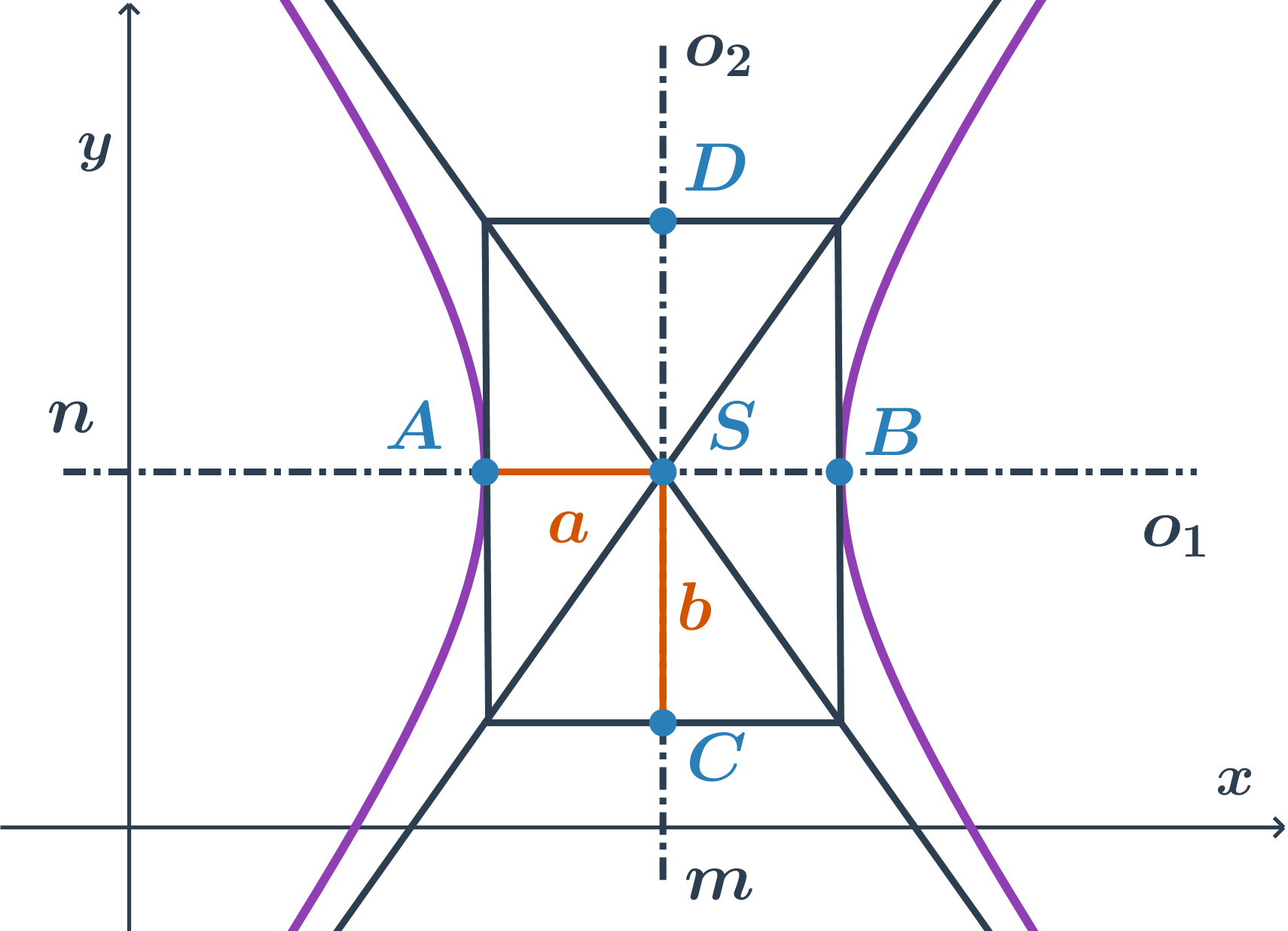
Stredová rovnica hyperboly s hlavnou osou rovnobežnou s osou y
Ak je hlavná os rovnobežná s osou y, rovnica je v tvare -\frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1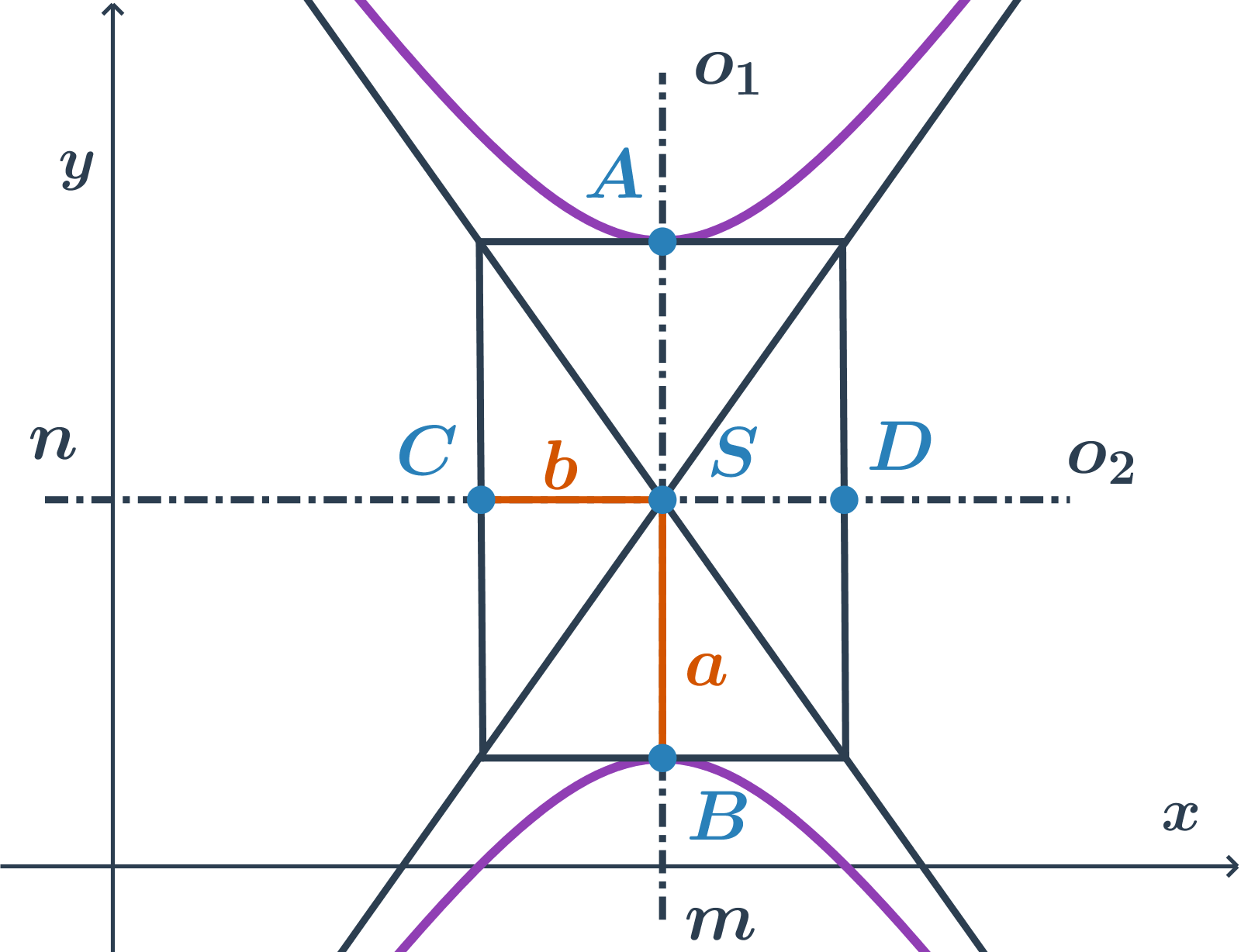
Oproti elipse, nemusí byť v prípade hyperboly vždy hlavná polos a dlhšia než vedľajšia polos b. Pre rovnoosú hyperbolu dokonca platí a=b.
Ako zo stredovej rovnice poznáme, s ktorou súradnicovou osou je rovnobežná hlavná os hyperboly?
- Pozrieme sa na znamienka členov s premennou x a y.
- Premenná v člene, ktorý má pred sebou znamienko plus udáva, s ktorou súradnicovou osou je rovnobežná hlavná os hyperboly.
- V menovateli danej premennej je potom (v druhej mocnine) veľkosť hlavnej polosi.
- Stručne povedané: ak je znamienko plus napríklad v prípade člena s premennou x, je hlavná os rovnobežná s osou x a v menovateli je druhá mocnina veľkosti hlavnej polosi a.
Príklad: Určenie stredovej rovnice hyperboly
Určite stredovú rovnicu hyperboly so stredom v bode S[1;-5], ak je veľkosť hlavnej polosi 2, veľkosť vedľajšej polosi 6 a hlavná os je rovnobežná s osou y.
- Stredová rovnica je v tvare -\frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1. Hlavná polos má veľkosť a, vedľajšia b.
- Dosadíme súradnice stredu a veľkosti hlavnej a vedľajšej polosi. Pri dosadení si dáme pozor na to, že súradnice stredu odčítame: -\frac{(x-1)^2}{6^2} +\frac{(y-(-5))^2}{2^2}=1
- Po úprave: -\frac{(x-1)^2}{36} +\frac{(y+5)^2}{4}=1
Rovnice asymptot
Už vieme, že asymptoty sú priamky, ku ktorým sa hyperbola blíži. Pomôžu pri vykreslení hyperboly. Rovnica asymptot závisí od tvaru stredovej rovnice hyperboly.
Pre hyperbolu danú rovnicou v tvare \frac{(x-m)^2}{a^2} -\frac{(y-n)^2}{b^2}=1 sú rovnice asymptot:
y=\pm\frac{b}{a}(x-m)+n
Pre hyperbolu danú rovnicou v tvare -\frac{(x-m)^2}{b^2} +\frac{(y-n)^2}{a^2}=1 sú rovnice asymptot:
y=\pm\frac{a}{b}(x-m)+n
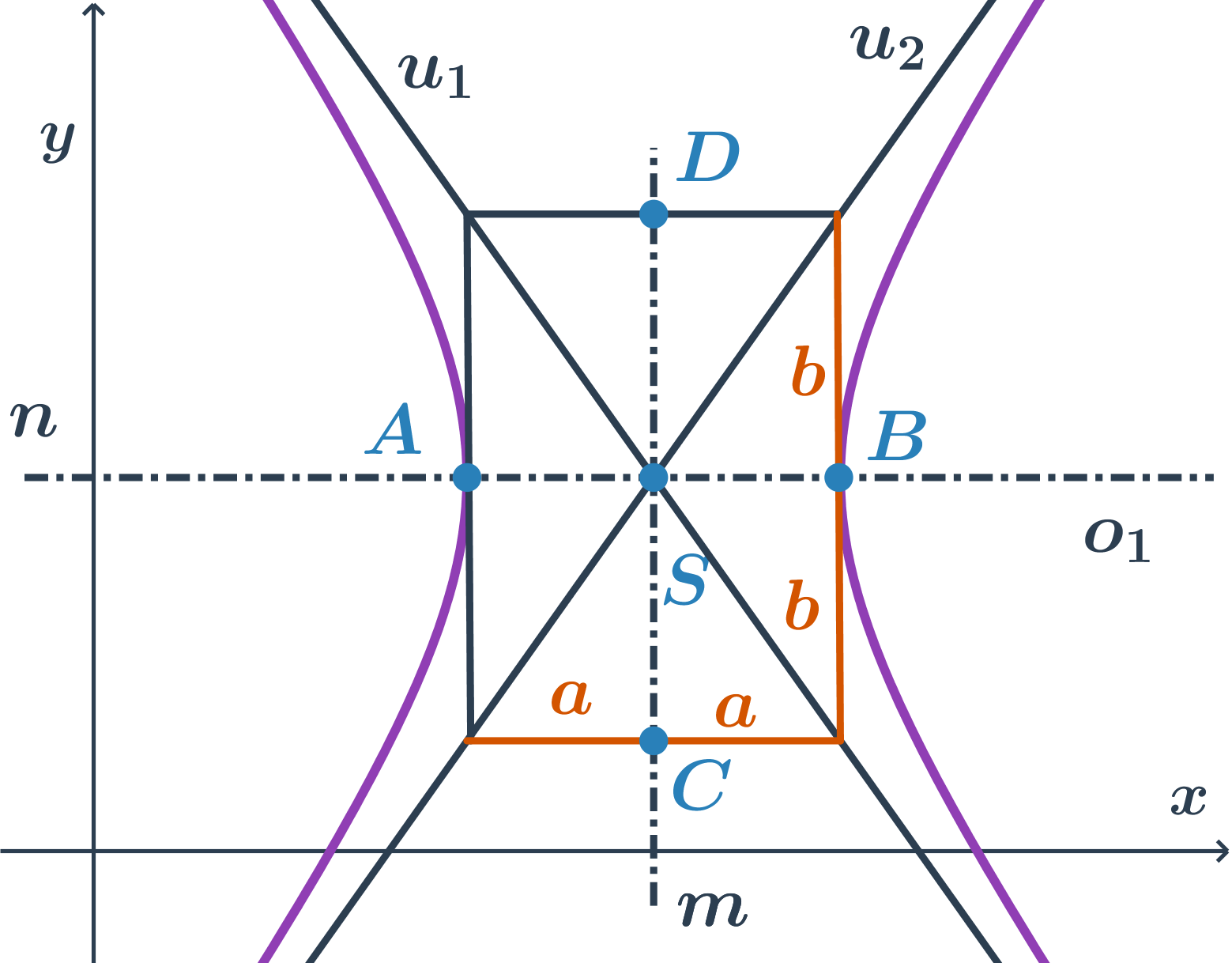
Ako načrtnúť hyperbolu?
- Najskôr si vyznačíme stred, hlavné a vedľajšie vrcholy.
- Potom zostrojíme charakteristický obdĺžnik hyperboly. To je obdĺžnik, ktorý má strany rovnobežné s osami a vrcholmi hyperboly sú stredy jeho strán. Dĺžky jeho strán sú teda 2a a 2b.
- Asymptoty sú uhlopriečky charakteristického obdĺžnika.
Všeobecná rovnica hyperboly
Podobne ako existuje niekoľko rovníc elipsy, môžeme aj rovnicu hyperboly zapísať rôznymi spôsobmi. Všeobecná rovnica hyperboly je v tvare: Ax^2 +By^2+Cx+Dy+E=1, A\cdot B \lt 0. Podmienka A\cdot B \lt 0 zaručuje, že konštanty A, B majú opačné znamienka. Každá rovnica v tomto tvare ale nemusí byť všeobecnou rovnicou hyperboly. Praktické overenie, či ide o hyperbolu vykonávame prevedením na stredovú rovnicu.
Príklad: Určuje daná rovnica hyperbolu?
Rozhodnite, či rovnica -x^2+2y^2+8x-18y+31=0 určuje hyperbolu.
- Najskôr si usporiadame členy: -x^2+8x+y^2-18y+40=0.
- Z členov s premennou x vytkneme -1: -(x^2-8x)+y^2-18y+40=0
- K obom stranám rovnice pripočítame konštantu 81 a odčítame konštantu 16, aby sme členy s premennými x a y mohli upraviť podľa vzťahu pre (a\pm b)^2: -(x^2-8x+16)+y^2-18y+81+40=81-16
- A upravíme: -(x-4)^2 +(y-9)^2+40=65
- Prevedieme konštantu 40 na druhú stranu rovnice: -(x-4)^2 +(y-9)^2 =25
- Na záver rovnice vydelíme 25: -\frac{(x-4)^2}{25} +\frac{(y-9)^2}{25}=1
- Ide teda o hyperbolu. Hlavná os je rovnobežná s osou y a a=b=5.
Hyperbola a priamka
- priamka s pretína hyperbolu v dvoch bodoch – sečnica hyperboly
- priamka t pretína hyperbolu v jednom bode – dotyčnica hyperboly
- priamka v hyperbolu nepretína – vonkajšia priamka hyperboly
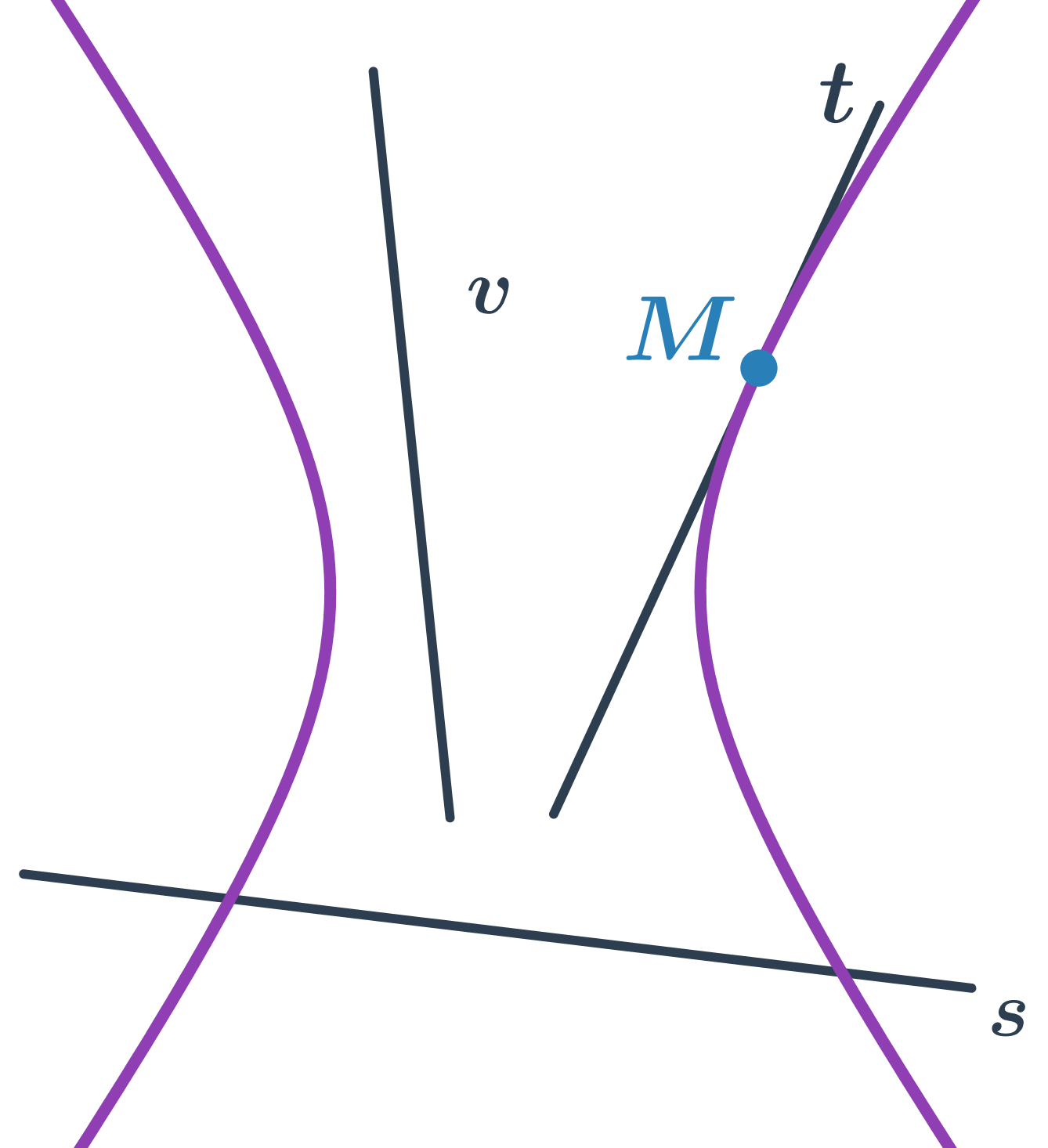
Špeciálnou polohou sečnice hyperboly je priamka, ktorá je rovnobežná s asymptotou. Taká sečnica potom pretína hyperbolu v jednom bode. 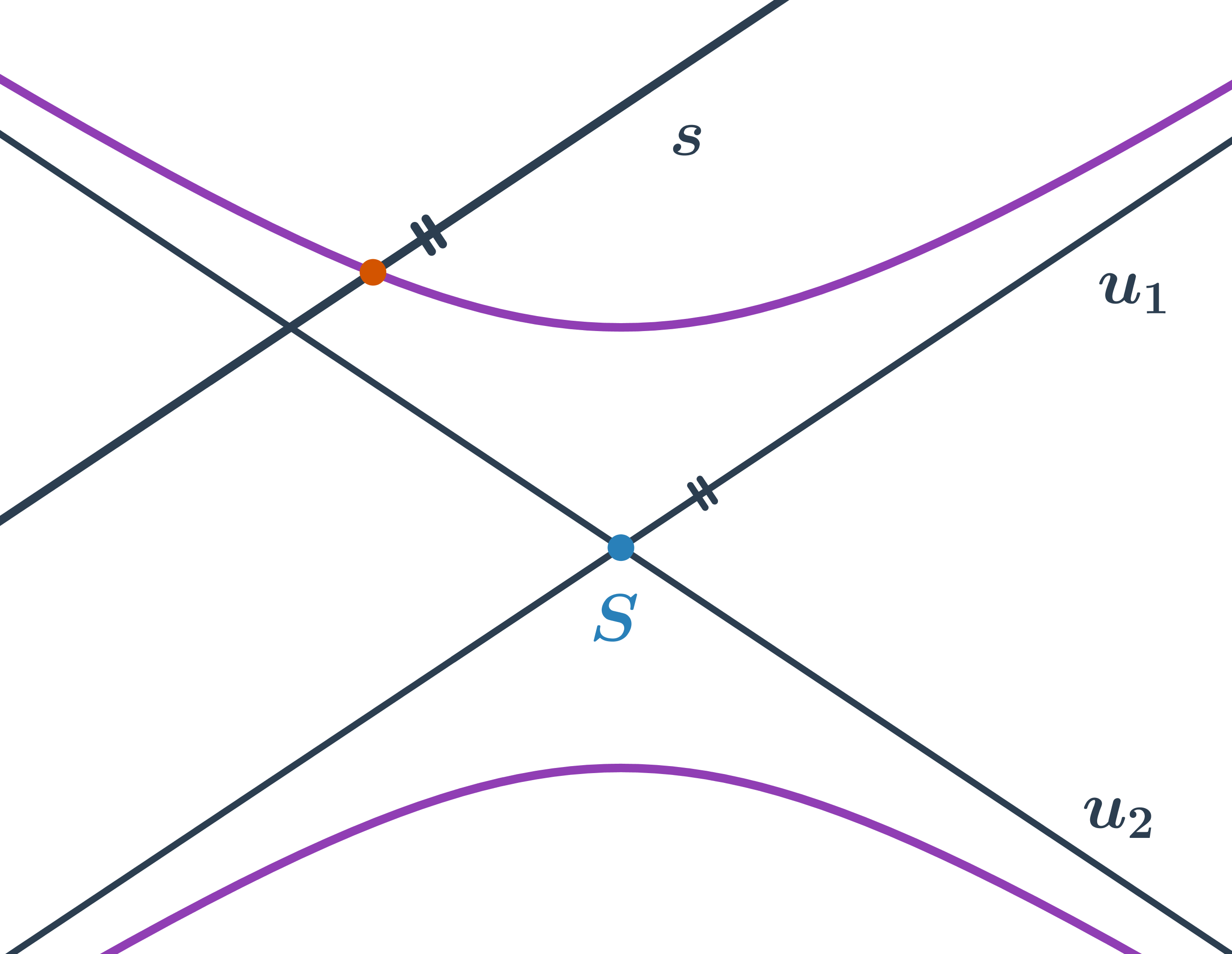
Ako rozlíšiť, či je priamka dotyčnica alebo sečnica?
- Najskôr určíme vzájomnú polohu priamky a hyperboly.
- Ak vyjdú dva priesečníky, ide o sečnicu vo všeobecnej polohe.
- Ak vyjde jeden priesečník, musíme ešte rozhodnúť, či je priamka rovnobežná s asymptotou. Ak nie, ide o dotyčnicu. V opačnom prípade ide o sečnicu.
Rovnica dotyčnice hyperboly v bode, ktorý leží na hyperbole
Hyperbola daná rovnicou \frac{(x-m)^2}{a^2} -\frac{(y-n)^2}{b^2}=1 má v bode T[x_0;y_0] dotyčnicu danú rovnicou:
\frac{(x-m)(x_0-m)}{a^2} -\frac{(y-n)(y_0-n)}{b^2}=1.
Podobne môžeme zapísať aj rovnicu dotyčnice hyperboly, ktorá má hlavnú os rovnobežnú s osou y.
Hore
